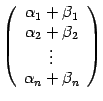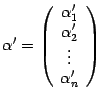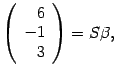Координаты и преобразования координат в линейном пространстве
Координаты векторов в данном базисе линейного пространства
Пусть — базис линейного пространства
. Каждый вектор
можно разложить по базису (см. теорему 8.1), т.е. представить в виде
, причем коэффициенты
в разложении определяются однозначно. Эти коэффициенты
называются координатами вектора
в базисе
(или относительно базиса
). Координаты
вектора
— это упорядоченный на бор чисел, который представляется в виде матрицы-столбца
и называется координатным столбцом вектора
(в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора
по базису
можно записать следующим образом:
(8.6)
Здесь умножение символической матрицы-строки на числовую матрицу-столбец
производится по правилам умножения матриц.
При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора
в базисе
.
Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы.
Линейные операции в координатной форме
Пусть — базис линейного пространства
, векторы
и
имеют в этом базисе координаты
и
соответственно, т.е.
(8.7)
Складывая эти равенства, получаем .
т.е. при сложении векторов их координаты складываются.
Умножая второе равенство в (8.7) на число , получаем
т.е. при умножении вектора на число все его координаты умножаются на это число.
Другими словами, сумма векторов имеет координаты
, а произведение
имеет координаты
. Разумеется, что все координаты получены в одном базисе
.
Замечания 8.5
1. Нетрудно показать, что координатный столбец линейной комбинации векторов
равен линейной комбинации
координатных столбцов
этих векторов.
2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и
. Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов
и система
их координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.
4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства
и всеми столбцами n-мерного арифметического пространства
. Это соответствие обозначается
. Для n-мерного комплексного линейного пространства
аналогичное взаимно однозначное соответствие устанавливается с пространством
.
Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства и
. Базис
будем условно называть «старым», а базис
— «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:
(8.8)
Записывая по столбцам координаты векторов в базисе
, составляем матрицу:
(8.9)
Квадратная матрица , составленная из координатных столбцов векторов нового базиса
в старом базисе
, называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:
(8.10)
Умножение символической матрицы-строки на матрицу перехода
в (8.10) производится по правилам умножения матриц.
Пусть в базисе вектор
имеет координаты
, а в базисе
— координаты
, т.е.
или, короче,
Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора
в одном и том же базисе
. Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому
(8.11)
Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе.
Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:
Доказать, что каждая система является базисом пространства . Найти матрицу
перехода от базиса
к базису
. Определить координаты квадратного трехчлена
относительно базисов
и
.
Решение. Система многочленов является стандартным базисом пространства
. Докажем, что система
является базисом. По ступим следующим образом. Найдем координатные столбцы
этих многочленов в стандартном базисе. Раскладывая по базису
, получаем
Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как
. Следовательно, столбцы
линейно независимы, тогда и многочлены
линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены
являются базисом пространства
, а матрица
— искомая матрица перехода от базиса
к базису
. Осталось найти координаты многочлена
в этих базисах. Раскладывая
по базисам, находим
Проверим результат, вычисляя по формуле (8.11):
Результаты совпадают.
Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса пространства
и известны матрицы перехода:
от базиса
к базису
;
от
к
;
от
к
. Тогда
(8.12)
Действительно, запишем связь (8.10) для данных базисов:
Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).
2. Если — матрица перехода от базиса
к базису
, то матрица
обратима и обратная матрица
является матрицей перехода от базиса
к базису
. Координаты вектора
в базисах
и
связаны формулами:
В самом деле, пусть — матрица перехода от базиса
к базису
. Учитывая, что матрица перехода от базиса
к базису
— единичная, применяем свойство 1 к трем базисам
. Для трех базисов
аналогично получаем:
. Следовательно,
.
3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве даны два базиса:
и
. Найти матрицу
перехода от базиса
к базису
и координаты вектора
в каждом из базисов.
Решение. Рассмотрим стандартный базис пространства
. Находим координаты векторов
в стандартном базисе. Раскладываем вектор
В стандартном базисе пространства
координатный столбец
совпадает с вектором
. Для других векторов аналогично получаем
. Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса
к данным базисам
и
По свойству 1 матриц перехода имеем . .По свойству 2:
. Поэтому
В стандартном базисе пространства
координатный столбец
совпадает с вектором
. Найдем координаты этого вектора в базисе
(по свойству 2 матрицы перехода):
В самом деле, справедливо разложение
Найдем координаты вектора в базисе
двумя способами
Полученный результат подтверждает разложение:
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Теорема доказана.
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $overrightarrow=left$, $overrightarrow=$, тогда
Теорема доказана.
Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.
Доказательство.
Теорема доказана.
Пример задачи на нахождение координат вектора
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 04 2022
Координаты вектора в декартовой системе координат (ДСК)
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y ).
Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.
Координатные векторы
Векторы i → и j → называются координатными векторами для заданной системы координат.
Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.
Разложение вектора
Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .
Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.
Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = ( 2 ; — 3 ) означает, что вектор a → имеет координаты ( 2 ; — 3 ) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .
Также имеет место быть нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 · i → + 0 · j → .
Равные и противоположные векторы
Векторы a → и b → равны тогда, когда их соответствующие координаты равны.
Противоположным вектором называется вектор противоположный данному.
Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = ( — a x ; — a y ) .
Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения ( a x ; a y ; a z ) называются координатами вектора в данной (трехмерной) системе координат.
Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ) , j → = ( 0 ; 1 ; 0 ) , k → = ( 0 ; 0 ; 1 ) , координаты нулевого вектора также равны нулю 0 → = ( 0 ; 0 ; 0 ) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = ( — a x ; — a y ; — a z ) .
Координаты радиус-вектора точки
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
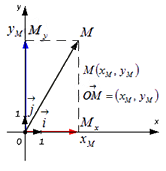
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M ( x M ; y M ) .
Вектор O M → называется радиус-вектором точки M .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты ( x M ; y M ) в данной системе координат.
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Аналогично в трехмерном пространстве радиус-вектор точки M ( x M ; y M ; z M ) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = ( x M ; y M ; z M ) .
Координаты и преобразования координат в линейном пространстве
Координаты векторов в данном базисе линейного пространства
Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:
Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.
При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .
Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .
Линейные операции в координатной форме
Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.
Складывая эти равенства, получаем .
т.е. при сложении векторов их координаты складываются .
Умножая второе равенство в (8.7) на число , получаем
т.е. при умножении вектора на число все его координаты умножаются на это число .
Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .
1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.
2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.
4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .
Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:
Записывая по столбцам координаты векторов в базисе , составляем матрицу:
Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:
Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.
Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.
Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому
Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .
Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:
Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .
Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем
Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим
Проверим результат, вычисляя по формуле (8.11):
Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда
Действительно, запишем связь (8.10) для данных базисов:
Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).
2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:
В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .
3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.
Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор
В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и
По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому
В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):
В самом деле, справедливо разложение
Найдем координаты вектора в базисе двумя способами
Полученный результат подтверждает разложение:
http://zaochnik.com/spravochnik/matematika/vektory/koordinaty-vektora-v-dsk/
http://mathhelpplanet.com/static.php?p=pryeobrazovaniya-koordinat-v-linyeinom-prostranstve
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 


вектору 
обозначен 
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора 
длина отрезка и обозначается 

не имеет. Вектор 
направление которого совпадает с направлением вектора 

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора 
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора 

свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства 
представлен в виде разности двух векторов, исходящих из начала координат: 


координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
При λ>0
– вектор





4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 


знаком «+», если вектор 
знаком «–», если 
Если
в качестве оси l взять некоторый другой вектор 


Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора 
вектора 
между вектором и осью, то есть 
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 


число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Теорема 2.3. Скалярное произведение двух векторов 
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами 

Отсюда
следует условие перпендикулярности ненулевых векторов



Нахождение проекции вектора 
заданное вектором 

С помощью скалярного произведения векторов находят
работу постоянной силы 
прямолинейном участке пути.
Предположим, что под действием постоянной силы 
положения А в положение B. Вектор силы 



равна 
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
соответствующего ресурса 
Тогда 
ресурсов 
векторов 
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала


Угол φ между 

формуле (2.29), то есть
6. Три некомпланарных вектора 
тройку, если при наблюдении из конца третьего вектора 
поворот от первого вектора 
вектору 
если по часовой стрелке.
Векторным
произведением 


вектор 
– 


– имеет длину, равную 


– векторы 
тройку (рис. 2.15).

условием коллинеарности двух векторов является равенство нулю их векторного
произведения 
Теорема 2.5. Векторное произведение векторов 
третьего порядка вида

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
построенного на векторах 


. Следовательно,

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы 
точки O называется вектор 
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
— 


Следовательно,
момент силы 
точки O представляет собой векторное произведение


Линейная скорость 
угловой скоростью 
неподвижной оси, определяется формулой Эйлера 
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 

. Следовательно, искомая площадь равна 
площади)
7. Рассмотрим произведение трех векторов 

результирующий вектор – скалярно на третий. Такое произведение 
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

Нетрудно показать, что объем параллелепипеда,
построенного на векторах 
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
Объем треугольной пирамиды, построенной на этих же
векторах, равен

Пример 2.13. Вершинами пирамиды служат точки 
Решение. Найдем
координаты векторов

По формуле (2.36) объем пирамиды, построенной на
векторах 


Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
линейно зависимой, если существуют такие числа 
место равенство

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
получим выражение вектора 
остальные векторы
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все


независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа

вектора 
векторов 
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт 
линейно независимых векторов, то есть каждый вектор 
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт 

по ортам 

пространстве.
Вопросы для самопроверки
Координаты векторов
Определение
18.4 Пусть
—
-мерное
линейное пространство, вещественное
или комплексное,
—
базис. Тогда произвольный вектор
из
представим
в виде линейной комбинации векторов
базиса:
Числа
называются
координатами вектора
в
базисе
.
Столбец
из
координат вектора называется координатным
столбцом вектора
.
Предложение
18.3 Координаты вектора
в заданном базисе определяются однозначно.
Доказательство.
Предположим противное. Пусть
—
базис, в котором у вектора
есть
два различных набора координат:
Тогда
то есть
Так как наборы координат различны, то
хотя бы один из коэффициентов справа
отличен от нуля. Следовательно, векторы
—
линейно зависимы, что противоречит
определению базиса. Полученное
противоречие означает, что предположение
о наличии двух различных наборов
координат неверно.
Предложение
18.4 Пусть в
-мерном
пространстве
задан
базис
.
Тогда координатный столбец суммы
векторов равен сумме координатных
столбцов слагаемых, координатный столбец
произведения вектора на число равен
координатному столбцу вектора, умноженному
на это число.
Доказательство.
Пусть векторы
и
имеют
координатные столбцы
и
соответственно.
Отсюда следует, что
Поэтому
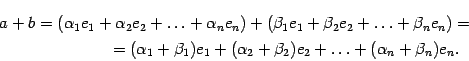
Это равенство означает, что координатный
столбец вектора
имеет
вид
.
Первая часть предложения доказана.
Доказательство второй части предоставляем
читателю.
Из последнего
предложения следует, что как только в
-мерном
пространстве зафиксирован базис, каждый
вектор можно заменить его координатным
столбцом, и операциям сложения и умножения
на число соответствуют такие же операции
над их координатными столбцами. Таким
образом, каждое
-мерное
пространство является, с точки зрения
алгебры, копией пространства
в
вещественном случае, а в комплексном —
копией
.
Изменение
координат вектора при изменении базиса
Пусть в
-мерном
линейном пространстве
выбран
базис
,
который мы будем для удобства называть
«старый» и другой базис
,
который мы будем называть «новый».
Возьмем призвольный вектор
из
.
Его координатный столбец в старом базисе
обозначим
,
а в новом —
.
Нам нужно выяснить, как связаны друг с
другом координаты в старом и в новом
базисе. Для этого нам сначала нужно
«связать» друг с другом старый и
новый базисы. Запишем разложения новых
базисных векторов по старому базису
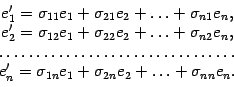
Составим матрицу, столбцами которой
служат координатные столбцы векторов
нового базиса

Эта матрица
называется матрицей перехода от
старого базиса к новому.
Замечание
18.1 Матрица перехода
всегда невырождена, то есть
.
Предложение
18.5 Координатные
столбцы в старом базисе и в новом базисе
связаны формулой
|
|
(18.1) |
где справа стоит произведение матрицы
перехода
на
матрицу-столбец.
Доказательство.
Так как
—
координатный столбец вектора
в
новом базисе, то

Заменив векторы
их
разложениями по старому базису, получим
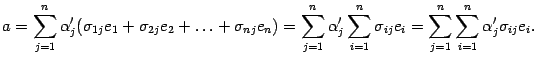
В силу предложения
14.3 изменим порядок суммирования
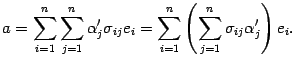
Здесь мы получили разложение вектора
по
старому базису, причем координата
вектора с номером
равна
.
Элемент с номером
столбца
будет
иметь такой же вид. Следовательно,
формула (18.1)
доказана.
Пример 18.4
Пусть
,
то есть
—
трехмерное векторное пространство.
Пусть задан ортонормированный базис
i, j, k. Выберем другой (новый)
базис
Возьмем вектор
.
Найдем его координаты в новом базисе.
Выпишем матрицу
перехода, ее столбцы — это координаты
новых базисных векторов
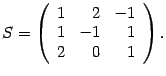
Пусть
—
координатный столбец вектора
в
новом базисе. Тогда
|
|
(18.2) |
откуда
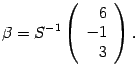
Найдем матрицу
по
формуле (14.14).
Находим определитель
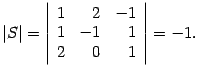
Находим алгебраические дополнения
Следовательно,
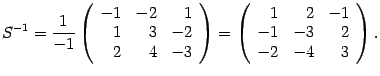
Находим координаты вектора

Таким образом, новые координаты вектора
:
,
,
,
.
Тот же самый
результат можно было получить, записав
формулу (18.2)
в виде системы уравнений
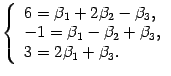
Решив эту систему, например, методом
Гаусса, найдем новые координаты
,
,
.
Вперед:
Матрица
линейного преобразования
Наверх:
Линейные
преобразования
Назад:
Линейные
преобразования
Определение и
примеры
Рассмотрим линейное
пространство
и
преобразование
этого
пространства, то есть закон, по которому
каждому вектору
из
соответствует
вектор
из
того же пространства. Вектор
называется
образом
вектора
и
обозначается
,
а вектор
называется
прообразом
вектора
.
Определение
19.1
Преобразование
линейного
пространства
называется
линейным,
если для любых векторов
и
и
любого числа
выполнены
равенства
|
|
(19.1) |
то есть образ
суммы векторов равен сумме образов
слагаемых, образ вектора, умноженного
на число, равен произведению этого числа
на образ вектора.
Замечание
19.1 В этой
главе с каждым линейным преобразованием
будет связана матрица, которую мы будем
обозначать той же буквой, что и само
преобразование. Чтобы их различать, мы
для букв, обозначающих преобразование,
будем использовать так называемый
«каллиграфический» шрифт.
Линейное
преобразование пространства
называют
также линейным
отображением
из
в
или
линейным
оператором
из
в
.
Исходя из
равенств (19.1)
легко проверить, что
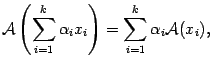
то есть образ
линейной комбинации векторов равен
линейной комбинации их образов.
Рассмотрим несколько
примеров линейных преобразований.
Пример
19.1 Пусть
—
двумерное векторное пространство, то
есть множество векторов плоскости.
Пусть
.
Это преобразование действует так: каждый
вектор оно переводит в вектор такого
же направления, но в два раза большей
длины. Если считать, что все векторы
имеют начало в начале координат, то
преобразование
можно
представить как растяжение плоскости
в два раза (рис. 19.1).
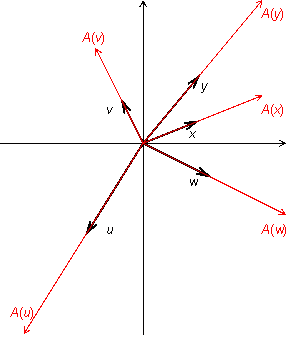
Рис.19.1.Преобразование растяжения
Проверим выполнение
равенств (19.1)
Равенства (19.1)
выполнены, следовательно, преобразование
является
линейным.
Пример
19.2 Пусть
—
двумерное векторное пространство,
—
поворот вектора по часовой стрелке на
угол
(рис.
19.2).
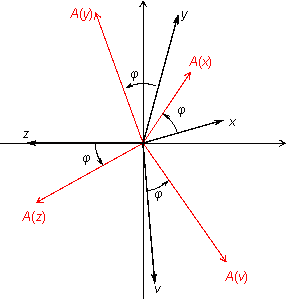
Рис.19.2.Преобразование поворота
Покажем, что это
— линейное преобразование.
Пусть
и
—
два вектора. Тогда
—
это диагональ параллелограмма со
стронами
,
(рис.
19.3).
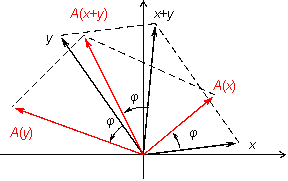
Рис.19.3.Образ суммы векторов
Если параллелограмм
повернуть как единое целое на угол
,
то его стороны станут векторами
и
,
диагональ будет вектором
.
С другой стороны, диагональ тоже
повернулась на угол
и
поэтому является вектором
.
Следовательно,
,
первое из условий (19.1)
выполнено.
Пусть
—
число. Из рисунка 19.4 очевидно, что
.
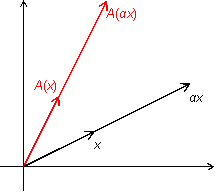
Рис.19.4.Образ вектора, умноженного на
число
Следовательно,
преобразование
—
линейное.
Упражнение19.1.1.
Пусть
—
двумерное векторное пространство,
—
некоторая прямая, проходящая через
начало координат,
—
преобразование, переводящее каждый
вектор
в
вектор
симметричный
исходному относительно прямой
(рис.
19.5). Другими словами,
является
зеркальным отражением вектора
в
прямой
.
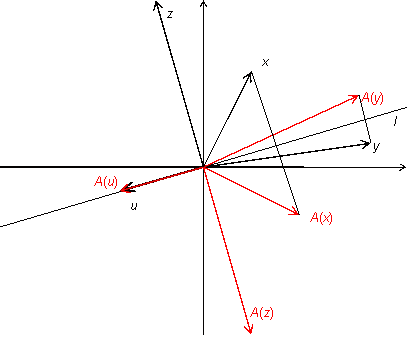
Рис.19.5.Преобразование отражения
Докажите, что
является
линейным преобразованием.
Упражнение19.1.2.
Пусть
—
двумерное векторное пространство,
—
некоторая прямая, проходящая через
начало координат,
—
преобразование, переводящее каждый
вектор
в
его проекцию на прямую
(рис.
19.6).
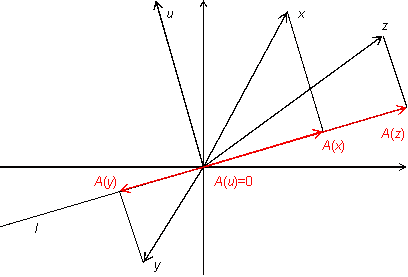
Рис.19.6.Преобразование проектирования
Докажите, что
является
линейным преобразованием.
Пример
19.3 Пусть
—
пространство всех многочленов,
—
преобразование, которое переводит
вектор из
,
то есть многочлен, в производную этого
многочлена, которая естественно является
многочленом, то есть вектором из
.
Пусть
,
то есть
.
Тогда
Например, если
,
то
.
Покажем, что преобразование
является
линейным.
Пусть
,
—
число. Тогда в силу свойства линейности
производной получим
Аналогично,
Следовательно,
—
линейное преобразование.
Пример
19.4 Пусть
—
-мерное
линейное пространство, Выберем в этом
пространстве базис
.
Тогда у любого вектора
есть
его координатный столбец
.
Пусть
—
квадратная матрица порядка
.
Определим преобразование
следующим
образом:
является
вектором, координатный столбец которого
равен
(справа
стоит произведение матрицы
на
столбец
).
Покажем, что преобразование
—
линейное.
Пусть
и
имеют
координатные столбцы
и
соответственно,
а их образы
и
—
координатные столбцы
,
и
.
Тогда
Но выражение в
последнем равенстве справа является
координатным столбцом образа суммы
векторов
.
Следовательно,
.
Пусть
—
произвольное число. Тогда координатный
столбец вектора
равен
,
координатный столбец образа вектора
то есть равен числу
,
умноженному на координатный столбец
образа вектора
.
Поэтому
.
Тем самым мы доказали, что преобразование
является
линейным.
Очевидно, что
примерами линейных преобразований
могут служить тождественное
преобразование,
то есть преобразование, переводящее
каждый вектор в себя,
,
и нулевое
преобразование,
переводящее каждый вектор в нуль,
.
Легко проверяется,
что для любого линейного преобразования
образ
нуля равен нулю,
.
Действительно, в силу второго из
равенств (19.1)
Вперед:
Матрица
линейного преобразования
Наверх:
Линейные
преобразования
Назад:
Линейные
преобразования
Вперед: Координаты
векторов Наверх: Линейные
пространства Назад:
Определение
и примеры
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- n-мерный вектор и векторное пространство
- Линейные (векторные) n — мерные пространства
- Линейные операции над n — измеримыми векторами
- Скалярное произведение двух векторов
- Линейная зависимость и независимость векторов
- Базис n -мерного пространства. Разложение вектора по базису
- Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
- Однородная система уравнений. Особенности решения
n-мерный вектор и векторное пространство
Множество всех векторов, которые мы рассматривали на плоскости или в пространстве и для которых определены операции сложения векторов, умножение вектора на число являются простыми примерами векторного пространства.
Определение 1. Упорядоченное множество n действительных чисел, записанных в виде (a1, a2, a3, …, an) называется n- мерным вектором. Числа a1, a2, a3, …, an называются координатами вектора 

Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором 

Если у n-мерного вектора одна координата равна единице, а все остальные равны нулю, то такой вектор называется единичным. Очевидно, что существует n различных единичных векторов
исходящих из начала координат — точки О. Все определения и действия для двумерных и трехмерных векторов, заданных в координатной форме, распространяются и на n-мерные векторы (n ≥ 4).
Два n-мерных вектора равны тогда и только тогда, когда их соответствующие компоненты равны.
Вектор 

Суммой двух n-мерных векторов 




Произведением вектора 


Вектор, у которого все координаты равны нулю, называется нулевым вектором и обозначается
Операции над произвольными векторами удовлетворяют свойствам:
1. 
2. 
3. 
4. 
5. 
6. Существует нулевой вектор 


7. Для произвольного вектора 

8. 

Определение. Множество векторов с действительными координатами, в
котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие выше приведенным восьми свойствам, называется векторным пространством.
Замечания. Если под векторами 

Линейным пространством, например, множество всех алгебраических многочленов, степени которых не превышают натуральное число n. Если множество всех многочленов точно равно натуральному числу n, то не будет линейным пространством, потому что сумма двух многочленов может оказаться многочленом, степень которого меньше n.
Линейные (векторные) n — мерные пространства
Линейные 
В школьном курсе математики понятие вектора обозначалось как направленный отрезок. Положение (расположение) вектора на прямой 


Математический подход к изучению различных явлений (процессов) окружающего мира, в том, числе и экономических, требует обобщения понятия вектора, связано с увеличением количества его координат. Такое обобщение не подразумевает геометрической интерnретации, но является удобным для математического моделирования.
Вектором размерности 






Согласно определению 



Нулевым вектором 

Два вектора 

Линейные операции над n — измеримыми векторами
1. Суммой 



Следовательно:
Следствие. Для любого вектора 
2. Произведением вектора 




Следствие. Если 



Векторы 


Суммой взаимно противоположных векторов есть нулевой вектор той же размерности.
Разность векторов 



Векторы 




Если 
прямой или на параллельных прямых.
В частном случае, когда 

где 


Совокупность всех 


Скалярное произведение двух векторов
Аналогично тому, как рассматривался произведение матриц вводят понятие скалярного произведения векторов 


Скалярным произведением двух 
Действие умножения для получения скалярного произведения обозначают точкой между векторами:
Произведение 
На основе скалярного произведения приведем определение понятий, которые вводились для векторов размерностью 
Длиной 


то есть
Единичным 


Возведение любого ненулевого вектора к единичному называется его нормированием.
Среди единичных векторов выделяют векторы, для которых одна из координат равна единице, а все остальные — нулю. Такие векторы обозначают маленькой буквой 



В частности, в трехмерном пространстве эти векторы называются ортами координатных осей, они имеют собственные обозначения:
Кутом между двумя векторами 


Согласно (4.9) скалярное произведение можно рассматривать как общую числовую характеристику двух векторов.
Свойства скалярного произведения:
Линейное пространство, для которого определено скалярное произведение векторов со свойствами (4.10), называется евклидовым пространством.
В тeopии линейных пространств любое множество векторов одинаковой размерности называется системой векторов.
Пусть имеем систему, которая состоит из 







С помощью этой системы векторов систему линейных алгебраических уравнений с 
или кратко:
Действительно, если по правилам сложения векторов и умножения на скаляр умножить каждый вектор 


Замечания. На основе тeopии 
Линейная зависимость и независимость векторов
Пусть имеется система векторов 






Векторы называются линейно зависимыми, если хотя бы один из векторов системы является линейной комбинацией других. В противном случае, когда в системе векторов нет ни одного, который был бы линейной комбинацией других, векторы называются линейно независимыми.
Теорема 4.1 (про линейную зависимость системы векторов). Если среди чисел 

то система векторов 
Доказательство. Пусть в равенстве (4.14) среди чисел 

Отсюда получаем:
а согласно (4.13) это означает, что система векторов 

Последствие из теоремы 4.1 (о линейной независимости системы векторов).
Система векторов есть линейно независимой, если векторное равенство
выполняется только в случае 
Доказательство. Предположим, что система векторов линейно независима, и при этом существуют 

Одной из основных задач теории линейных пространств является задача исследования системы векторов на линейную независимость, то есть выяснения вопрос о том, какова есть заданная система векторов — линейно зависимой или линейно независимой.
Решение этой задачи сводится к решению систем линейных уравнений.
Запишем равенство (4.14) в координатной форме:
выполним умножение векторов системы на скаляры

По следствием из теоремы 4.1 система векторов линейно независимая, если система однородных уравнений (4.15) имеет только тривиальное решение: 

Проведем исследование на линейную независимость системы векторов:
Запишем векторное равенство:
Отсюда получаем систему уравнений:
Вычислим определитель основной матрицы системы:
Поскольку 

Преобразование основной матрицы системы по методу Жордана-Гаусса позволяет определить количество линейно независимых векторов в заданной системе векторов:
Ранг матрицы системы 
Подставляя найденные коэффициенты в векторное равенство (4.14), получим
Таким образом, векторы 





В линейной алгебре широко применяется система п единичных векторов 



Рассмотрим питания о наибольшее количество векторов, которое может содержать линейно независимая система 
Выберем из пространства 

запишем векторное равенство
и соответствующую ей однородную линейную систему 

Для ответа на поставленный вопрос будем исходить из сравнения количества векторов системы 

1. Если количество векторов больше измеримости пространства 


2. Если количество векторов равно размерности пространства 


Из проведенного анализа следует, что наибольшее количество линейно независимых векторов равно размерности линейного пространства.
Базис n -мерного пространства. Разложение вектора по базису
Понятие 






Теорема 4.2 (о разложении 
Произвольный вектор 


Доказательство. Согласно определению линейной комбинации системы векторов (4.13) надо показать существование единого набора цифр 

Представим векторы 

и запишем соответствующую систему линейных уравнений:
Поскольку определитель основной матрицы системы отличается от нуля (по условию векторы 
Представление вектора 


Система 



Запись 


Определение базиса пространства и разложения вектора по базису можно выполнять одновременно, аналогично тому, как выбор базисных неизвестных и нахождения решений СЛАУ осуществляли при применении методов Гаусса и Жордана-Гаусса.
Осуществить разложение вектора 

Для решения задачи представим вектор 


где 


Представим векторы 


Проверку на линейную независимость векторов 


Для этого запишем расширенную матрицу системы и проведем ее преобразования по методу Жордана-Гаусса:
Поскольку элементарными преобразования на месте основной матрицы системы получено единичную матрицу третьего порядка, то определитель исходной матрицы отличен от нуля, и система векторов 



Следовательно, координатами вектора 

В другом базисе вектор 

Любой вектор с 
Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
Представим произвольный вектор 

где 

Выясним, как можно осуществить переход от одного базиса линейного пространства к другому и найти координаты вектора 
Пусть в пространстве 


Запишем систему (4.17) в матричном виде: 
Неособенная матрица 


Можно показать, что зависимость между координатами вектора в разных базисах определяется формулами:
где 

Переход к новому базису широко используется в задачах линейного программирования и в других задачах математических методов в экономике.
Задан вектор 







В предыдущем примере было показано, что векторы 
Матрица перехода от базиса 



Транспонируем матрицу 
Для нее существует обратная матрица, поскольку 
По соотношению (4.18) определяем координаты вектора 


Рассмотрим разложение вектора по новому базису для нахождения базисных решений СЛАУ.
Запишем систему линейных алгебраических уравнений в векторной форме
где коэффициентами при неизвестных системы являются векторы 





Система линейных уравнений называется сводной к единичному базису, если среди векторов 

В общем случае, если количество векторов, образующих базис, меньше количества векторов системы 
Таким образом, для нахождения всех базисных решений системы можно предложить такой алгоритм:
1) сводим систему линейных уравнений элементарными преобразованиями к единичному базису;
2) находим значения неизвестных, что соответствуют данном базису, то есть координаты вектора 
3) выполняем преобразование системы уравнений с целью введения в базис других векторов системы. Тогда координаты вектора 
Заметим, что максимальное количество базисных решений равно количеству сопряжений с 


Найдем все базисные решения системы линейных уравнений
В векторной форме система уравнений имеет вид
где
Среди заданных векторов 

Есть четыре вектора двумерного пространства, среди которых необходимо определить базисные. Поскольку наибольшее количество линейно независимых векторов в этом пространстве равно двум, то все четыре вектора не могут быть линейно независимыми. Сводим систему линейных уравнений к единичному базису. Запишем матрицу коэффициентов системы в таблице 4.1 и выполним элементарные преобразования этой системы по методу Жордана-Гаусса.
Сведение системы уравнений к единичному базису Таблица 4.1
По результатам последней операции получено единичную матрицу.
Следовательно, векторы 








Количество базисов для данного примера определяется количеством соединений из четырех векторов 

В таблице 4.2 первым из базисных решений системы приведено именно то, которое получили в таблице 4.1.
Нахождение базисных решений Таблица 4.2
Заметим, что среди шестерых базисных решений данной системы линейных уравнений только 

В рамках учебной дисциплины 


Однородная система уравнений. Особенности решения
Рассмотрим векторный подход к нахождению общего решения систем линейных уравнений (1.9):
где 


В векторной форме система однородных линейных уравнений имеет вид:
где 




Если ранг основной матрицы меньше количества неизвестных 
Пусть коэффициенты при неизвестных 
где 

По свойству 3 (п. 3.2) любая линейная комбинация решений однородной системы также является решением этой системы.
Фундаментальной системой решений однородной системы уравнений называется такая линейно независимая система векторов 
Теорема 4.3 (пpo фундаментальную систему решений). Однородная система уравнений (4.20) имеет фундаментальную систему решений, количество векторов которой равно 

Доказательство. Предоставим свободным неизвестным 

(Конечно, при 
Выражения базисных неизвестных 


Вектор
где 
Если числа 


Следовательно, для нахождения общего решения однородной системы уравнений выполняем следующее:
1. Выражает базисные неизвестные системы (4.20) через свободные.
2. Предоставляем значение свободным 
3. Подставляемые в (4.21) последовательно значение свободных неизвестных (4.22), находим базисные неизвестные, получая таким образом фундаментальную систему решений:
4. Записываем общее решение системы как линейную комбинацию фундаментальных решений (4.23).
Найдем фундаментальную систему решений однородной системы уравнений:
Чтобы выразить базисные неизвестные системы через свободные неизвестные, воспользуемся методом Жордана-Гаусса. Выполняем элементарные преобразования основной матрицы системы для получения в ней единичной матрицы:
Выбираем за базисные неизвестные 


Если свободным неизвестным последовательно предоставить значения 





Общее решение системы уравнений в векторной форме находим как линейную комбинацию фундаментальных решений, а именно:
где
Тогда общее решение однородной системы уравнений, составленный из фундаментальных решений системы, имеет вид:
Замечания. Аналогично можно представить общее решение и неоднородной системы уравнений, которая имеет множество решений.
Пусть система неоднородных уравнений
совместима, но ранг матрицы системы меньше количества неизвестных 
где 
— общее решение (4.22) соответствующей однородной системы уравнений (4.20).
Найдем общее решение неоднородной системы уравнений:
Если праве части всех уравнений положить равными нулю, то получим однородной систему уравнений (4.24), общее решение которой определен в предыдущем примере:
где
Найдем произвольный частное решение неоднородной системы. Например, возьмем свободные неизвестные равными нулю: 



где
или
Такое представление общего решения неоднородной системы линейных алгебраических уравнений обобщается на произвольные неоднородные системы, которые имеют множество решений.
Лекции:
- Исследовать ряд на абсолютную сходимость
- Комплексные числа: примеры решения
- Уравнение окружности и прямой
- Область определения функции примеры решения
- Неопределенный интеграл
- Объемы многогранников
- Приложения определенного интеграла
- Дифференциальное вычисление функции одной переменной
- Решение слау
- Каноническое уравнение параболы