Как найти координаты вектора имея координаты точек - AvtoShod.ru

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Нахождение координат вектора
Примеры задач

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора


Для плоских задач	AB = {B_x — A_x; B_y — A_y}
Для трехмерных задач	AB = {B_x — A_x; B_y — A_y; B_z — A_z}
Для n-мерных векторов	AB = {B₁ — A₁; B₂ — A₂; … B_n — A_n}

Примеры задач

Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).

Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.

Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB_x + A_x = 6 + 2 = 8.
B_y = AB_y + A_y = 14 + 5 = 19.

Таким образом, B = (8; 19).

Источник

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y ; B_z — A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; … ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ — A₁ ; B₂ — A₂ ; … ; B_n — A_n}

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3 — 1; 1 — 4} = {2; -3}.

Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB_x = B_x — A_x => B_x = AB_x + A_x => B_x = 5 + 3 = 8
AB_y = B_y — A_y => B_y = AB_y + A_y => B_y = 1 + (-4) = -3

Ответ: B(8; -3).

Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).

Решение:

AB_x = B_x — A_x => A_x = B_x — AB_x => A_x = 3 — 5 = -2
AB_y = B_y — A_y => A_y = B_y — AB_y => A_y = -4 — 1 = -5

Ответ: A(-2; -5).

Примеры для пространственных задач

Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.

Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3
AB_z = B_z — A_z   =>   B_z = AB_z + A_z   =>   B_z = 2 + 3 = 5

Ответ: B(8; -3; 5).

Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5
AB_z = B_z — A_z   =>   A_z = B_z — AB_z   =>   A_z = 1 — 4 = -3

Ответ: A(-2; -5; -3).

Примеры для n -мерного пространства

Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.

Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).

Решение:

AB₁ = B₁ — A₁   =>   B₁ = AB₁ + A₁   =>   B₁ = 5 + 3 = 8
AB₂ = B₂ — A₂   =>   B₂ = AB₂ + A₂   =>   B₂ = 1 + (-4) = -3
AB₃ = B₃ — A₃   =>   B₃ = AB₃ + A₃   =>   B₃ = 2 + 3 = 5
AB₄ = B₄ — A₄   =>   B₄ = AB₄ + A₄   =>   B₄ = 1 + 2 = 3

Ответ: B(8; -3; 5; 3).

Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).

Решение:

AB₁ = B₁ — A₁   =>   A₁ = B₁ — AB₁   =>   A₁ = 3 — 5 = -2
AB₂ = B₂ — A₂   =>   A₂ = B₂ — AB₂   =>   A₂ = -4 — 1 = -5
AB₃ = B₃ — A₃   =>   A₃ = B₃ — AB₃   =>   A₃ = 1 — 4 = -3
AB₄ = B₄ — A₄   =>   A₄ = B₄ — AB₄   =>   A₄ = 8 — 5 = 3

Ответ: A(-2; -5; -3; 3).

Источник

Определение

Вектор – это направленный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор изображается в виде направленных отрезков определенной длины.

Рис. 1.

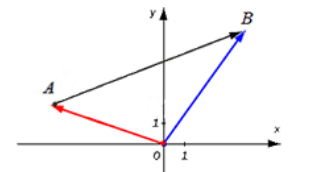
Вектор, имеющий начальную точку А и конечную точку В, обозначается [overrightarrow{A B}](рис. 1).

Определения

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора [overrightarrow{A B}]. Длина вектора [overrightarrow{A B}] обозначается как: [|overrightarrow{A B}|]

Векторы параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами.

Определение

Единичный вектор или орт — это вектор, длина которого равна единице.

Рис. 3.

Правило нахождения координат вектора

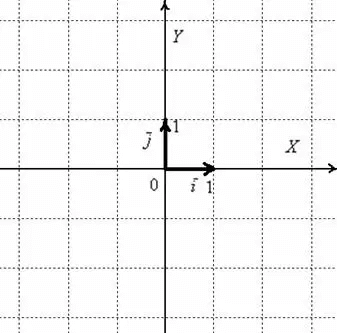
Отложим от начала системы координат два единичных вектора, то есть векторы, длины которых равны единице. Направление вектора [bar{i}] должно совпадать с осью [O x], а направление вектора [bar{j}] с осью [O y].

Векторы [bar{i}, bar{j}] — рассматриваемые векторы называются векторами координат или ортами. Эти векторы образуют базис поверхности. Иногда построенный базис называют ортонормированным базисом плоскости.

Обозначение: базис обычно пишется в круглых скобках, внутри которых в строгом порядке перечисляются векторы.

Любой вектор плоскости выражается по формуле нахождения координат вектора:

[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}]

Где числа в этом базисе называются векторными координатами. Но само выражение называется векторным разложением.

Как выразить вектор через его координаты

Чтобы выразить вектор [overrightarrow{A B}(a, b)], где [Aleft(x_{1} ; y_{1}right)], а [Bleft(x_{2} ; y_{2}right)], сначала вычислим разницу между абсциссами [x], чтобы получить [a], затем вычислим разницу между ординатами [y], чтобы получить [b]:

[overrightarrow{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)]

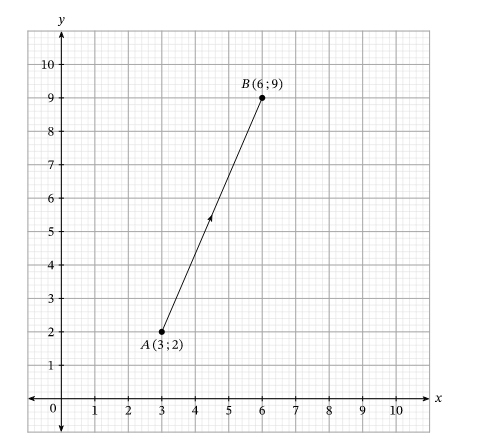
Пример 1

Найти координаты [overrightarrow{A B}] при значении координат точек [A(3 ; 2), B(6 ; 9)].

Рис. 4.

Решение:

Горизонтальное расстояние равно разнице между абсциссами [x], т.е. 6−3=3. Вертикальное расстояние равно разнице между ординатами [y], где 9−2=7.

Поэтому мы можем обозначить вектор от А до В как:

[overrightarrow{A B}=(3 ; 7)]

Нахождение координат вектора в пространстве

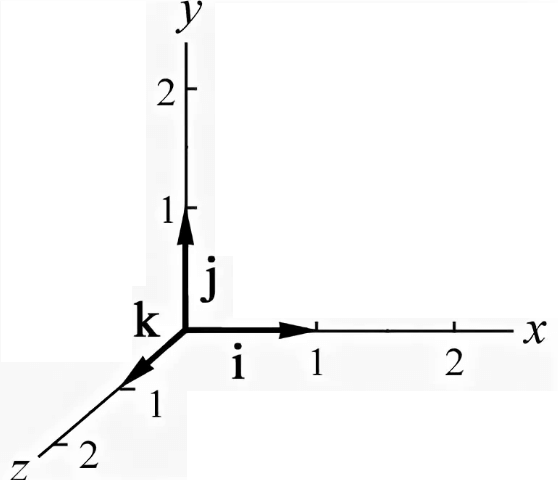
Теперь рассмотрим векторы в трехмерном пространстве, здесь все почти так же, как на плоскости, но будет добавлена только одна дополнительная координата.

Рис. 5.

Любой вектор в пространстве выражается следующим образом:

[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}+v_{3} cdot vec{k}], где координаты вектора (числа) в заданном базисе.

Пример 2

Нужно найти вектор, соединяющий точку А (начало) с координатами (4, 5, 6) с точкой В (конец) с координатами (10, 11, 12).

Решение:

Вектор направлен из точки А в точку В и может быть обозначен как [overrightarrow{A B}]. Таким образом:

[overrightarrow{A B}=(10-4) ;(11-5) ;(12-6)=(6 ; 6 ; 6)]

Нет времени решать самому?

Наши эксперты помогут!

Как записать вектор на основе единичных векторов

Если мы перейдем от начальной точки к конечной точке [Cleft(x_{y} ; y_{1}right) Dleft(x_{2} ; y_{2}right)], это описывает вектор, который представляет собой смещение на расстояние в направлении [overrightarrow{C D}left(x_{2}-x_{1}right) x] затем с расстояния в направлении [left(y_{2}-y_{1}right) y].

Рис. 6.

Мы можем обозначить этот вектор двумя способами:

[overrightarrow{C D}=left(x_{2}-x_{1}, y_{2}-y_{1}right)] или [overrightarrow{C D}=left(x_{2}-x_{1}right) i+left(y_{2}-y_{1}right) vec{j}]

Пример 3

Выразить вектор в виде суммы единичных векторов.

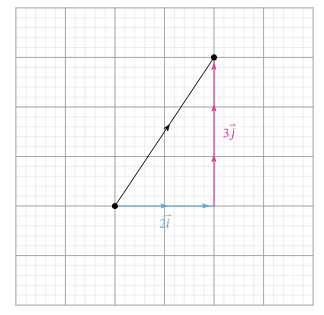
Зная, что каждый квадрат сетки имеет длину 1, представим вектор [overrightarrow{A B}] как [a vec{i}+b vec{j}].

Рис. 7.

Решение:

Из точки [A](начало), мы перемещаем единицы в горизонтальном направлении (которое представляет собой вектор), затем мы перемещаем единицы в вертикальном направлении (что представляет собой вектор), чтобы перейти к точке [B+2(2 vec{i}) u+3(3 vec{j})].

Вектор [overrightarrow{A B}] что представляет собой прямое движение от [A] к [B] , тогда равна сумме этих единичных векторов.

Рис. 8.

Как результат: [overrightarrow{A B}=2 vec{i}+3 vec{j}=(2,3)].

Использование векторов и позволяет описать вектор в соответствии с количеством шагов по горизонтали и вертикали длиной 1, которые необходимо сделать, чтобы пройти от начала до конца. Обратите внимание, что отрицательные коэффициенты представляют движение влево или вниз соответственно.

Рис. 9.

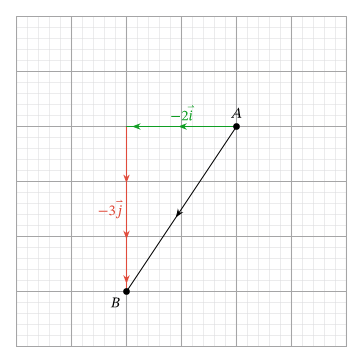
Например, приведенный выше вектор, представляющий смещение на -2 единицы в направлении и на -3 единицы в направлении [overrightarrow{A B}=(-2 ;-3) x y] или [(-2 vec{i})+(-3 vec{j})].

[overrightarrow{A B}=-2 vec{i}-3 vec{j}]

Важно

Следует понимать разницу между координатами точки и векторными координатами:

Координаты точки — это обычные координаты в прямоугольной системе координат. Каждая точка имеет строгое место на карте, и их нельзя никуда перемещать.

Координаты вектора — это его разложение относительно основания.

Любой вектор свободен, поэтому при желании или необходимости мы легко можем отложить его от другой точки плоскости. Записи координат точек и векторных координат выглядят одинаков, а значение координат совсем разные.

Координаты равных векторов соответственно равны.

Если точка начала вектора не совпадает с началом системы координат, тогда рассмотрим задачу. На оси [O_{x y}] заданы координаты точек вектора, где [Aleft(x_{a} ; y_{a}right)] и [Bleft(x_{b} y_{b}right)]. Найти координаты [overrightarrow{A B}].

Рис. 10.

Зная формулу сложения векторов, имеем [overrightarrow{O A}+overrightarrow{A B}=overrightarrow{O B}], следует: [overrightarrow{A B}=overrightarrow{O B}-overrightarrow{O A}].

[overrightarrow{O A}] и [overrightarrow{O B}] радиус-векторы точек А и В, следовательно, координаты точек: [overrightarrow{O A}=left(x_{a}, y_{a}right), overrightarrow{O B}=left(x_{b} ; y_{b}right)].

Источник

Содержание:

Формула
Примеры нахождения координат вектора по точкам

Формула

Чтобы найти координаты вектора $overline{A B}$ на плоскости, если он задан координатами своих начала $Aleft(x_{1} ; y_{1}right)$ и конца $Bleft(x_{2} ; y_{2}right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть

$$overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)$$

Чтобы найти координаты вектора $overline{A B}$, заданного в пространстве координатами $Aleft(x_{1} ; y_{1} ; z_{1}right)$ и $Bleft(x_{2} ; y_{2} ; z_{2}right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:

$$overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}right)$$

Примеры нахождения координат вектора по точкам

Пример

Задание. Даны точки
$A(4;-1)$ и $B(2;1)$. Найти координаты векторов $overline{A B}$ и
$overline{B A}$

Решение. Для вектора $overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline{A B}$ равны

$$overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)$$

Для вектора точка
$B$ является началом, а точка
$A$ — концом. Тогда координаты вектора $overline{B A}$ равны

$$overline{B A}=(4-2 ;-1-1)=(2 ;-2)$$

Ответ. $overline{A B}=(-2 ; 2), overline{B A}=(2 ;-2)$

Пример

Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов
$overline{A B}$,
$overline{A C}$,
$overline{B C}$

Решение. Для искомого вектора
$overline{A B}$ точка
$A$ является началом, а точка
$B$ — концом. Тогда координаты вектора
$overline{A B}$ соответственно равны:

$$overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$

Для вектора $overline{A C}$ точка
$A$ является началом, а точка
$C$ — концом. Тогда его координаты соответственно равны

$$overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)$$

Для вектора $overline{B C}$ точка
$B$ является началом, а точка
$C$ — концом. Его координаты равны

$$overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)$$

Ответ. $overline{A B}=(2 ; 4 ; 1), overline{A C}=(-1 ; 1 ; 0,5), overline{B C}=(-3 ;-3 ;-0,5)$

Читать дальше: как найти сумму векторов.

Как найти сумму векторов
Как найти скалярное произведение векторов
Как найти векторное произведение векторов
Как найти смешанное произведение векторов
Как найти вектор коллинеарный вектору
Как найти вектор перпендикулярный вектору
Как найти орт вектора
Как найти разность векторов
Как найти проекцию вектора
Как найти длину вектора
Как найти модуль вектора
Как найти координаты вектора
Как найти направляющие косинусы вектора
Как найти угол между векторами
Как найти косинус угла между векторами

Источник

Задачи с векторами только на первый взгляд кажутся сложными, особенно если задача связана с трехмерным пространством. Но не стоит пугаться ведь если разобраться по-лучше в данной тематике задачи решаются в два счета. Так например в данной статье мы разберем тематику определения координат вектора, исходными данными для которого известны координаты начальной и конечной точки.

Основное правило, которое будет сопровождать в данной теме, гласит так:

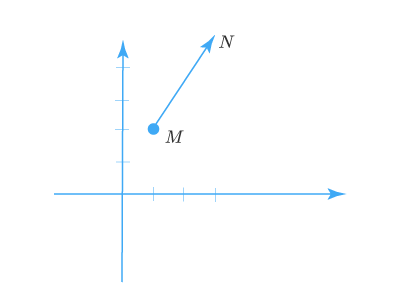
Для того чтобы определить координаты некоторого вектора MN⃗vec{MN}, зная координаты начала и конца, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Задача 1

Рассмотрим первый вариант задачи. Вектор задан в двухмерном пространстве {x,y}. Тогда у каждой точки вектора существует две координаты, соответственно относящиеся к оси ОХ и ОУ. Формула для определения координаты вектора в таком случае принимает вид:

MN⃗=Mx−Nx;My−Ny.vec{MN}={M_x{-N}_x;M_y{-N}_y}.

Рассмотрим на примере: На некоторой плоскости заданы точки M и N, координаты которых равны соответственно (1,2) и (3,5). Необходимо найти координаты вектора MN⃗vec{MN}

Решение

Возьмем некоторую плоскость ОХУОХУ и отметим точки ММ и NN. Затем соединим исходные точки и рассчитаем координаты полученного вектора. MN⃗={3−1;5−2}=2;3.vec{MN}=left{3-1;5-2right}={2;3}.

Вот так вот мы получили простое решение искомой задачи. Вариация таких задач может сочетать в себе нахождение не только координат вектора, но и отдельных координат исходных точек вектора.

Но у меня задача может быть не только одно- или двухмерное, но также трехмерное или как мы будем называть их n-мерное. Формула тогда в таком случае немного изменит вид, но смысл не меняется.

Задача 2

Сформулируем формулу для определения координат вектора расположенного в n-мерном пространстве.
Такое пространство подразумевает координаты точек в виде M(M1;M2;M3;..;Mn)M(M_1;M_2{;M}_3;..{;M}_n) и формула примет вид:

MN⃗=Mx−Nx;My−Ny;..;Mn−Nn.vec{MN}={M_x{-N}_x;M_y{-N}_y{;..;M}_n{-N}_n}.

Рассмотрим задачу на примере 5-мерного пространства. Необходимо найти координаты точки N вектора

MN⃗={3,8,4,1,7}vec{MN}={3,8,4,1,7}, если известны координаты точки M(1,9,6,7,4).M(1,9,6,7,4).

Решение

Не стоит пугаться при виде слов 5-мерное пространство, т.к. рисовать данную систему координат не обязательно. Стоит лишь правильно понимать и применять формулу которую мы рассмотрели выше. Перепишем ее еще раз для нашего случая.

MN⃗={M1−N1;M2−N2;M3−N3;M4−N4;M5−N5}.vec{MN}= {M_1{-N}_1;M_2{-N}_2{;M_3{-N}_3{;M}_4{-N}_4;M}_5{-N}_5}.

Тогда рассмотрим систему:

{1−N1=39−N2=86−N3=47−N4=14−N5=7begin{cases}1-N_1=3 \
9-N_2=8 \
6-N_3=4\
7-N_4=1\
4-N_5=7end{cases}

и решив данную систему, получим

{N1=−2N2=1N3=2N4=6N5=−3begin{cases}N_1=-2\
N_2=1\
N_3=2\
N_4=6\
N_5=-3\ end{cases}

Тогда получим ответ на задачу N(−2,1,2,6,−3).N(-2,1,2,6,-3).

Источник

Нахождение координат вектора

Примеры задач

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

Формула определения координат вектора для пространственных задач

Формула определения координат вектора для n -мерного пространства

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Примеры для пространственных задач

Примеры для n -мерного пространства

Правило нахождения координат вектора

Как выразить вектор через его координаты

Нахождение координат вектора в пространстве

Как записать вектор на основе единичных векторов

Формула

Примеры нахождения координат вектора по точкам

Задача 1

Задача 2

Не пропустите также: