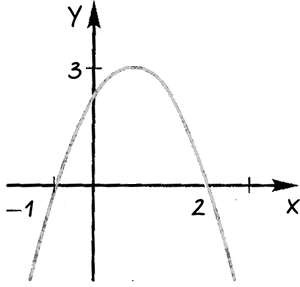Как найти координаты точки пересечения с осью - AvtoShod.ru

Точки пересечения графика осями

Как найти точки пересечения графика функции с осями координат?

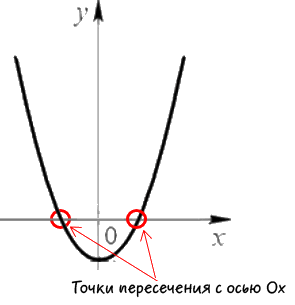
С осью абсцисс график функции может иметь любое количество общих точек (или ни одной). С осью ординат — не более одной (так как по определению функции каждому значению аргумента ставится в соответствие единственное значение функции).

Чтобы найти точки пересечения графика функции y=f(x) с осью абсцисс, надо решить уравнение f(x)=0 (то есть найти нули функции).

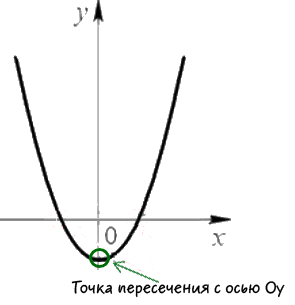
Чтобы найти точку пересечения графика функции с осью ординат, надо в формулу функции вместо каждого x подставить нуль, то есть найти значение функции при x=0: y=f(0).

1) Найти точки пересечения графика линейной функции y=kx+b с осями координат.

В точке пересечения графика функции с осью Ox y=0:

kx+b=0, => x= -b/k. Таким образом, линейная функция пересекает ось абсцисс в точке ( -b/k ; 0).

В точке пересечения с осью Oy x=0:

y=k∙0+b=b. Отсюда, точка пересечения графика линейной функции с осью ординат — (0; b).

Например, найдём точки пересечения с осями координат графика линейной функции y=2x-10.

2x-10=0; x=5. С Ox график пересекается в точке (5; 0).

y=2∙0-10=-10. С Oy график пересекается в точке (0; -10).

2) Найти точки пересечения графика квадратичной функции y=ax²+bx+c с осями координат.

В точке пересечения графика с осью абсцисс y=0. Значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью Ox, надо решить квадратное уравнение ax²+bx+c=0.

В зависимости от дискриминанта, парабола пресекает ось абсцисс в одной точке или в двух точках либо не пересекает Ox.

В точке пересечения графика с осью Oy x=0.

y=a ∙ 0²+b ∙ 0+c=с. Следовательно, (0; с) — точка, в которой парабола пересекает ось ординат.

Например, найдём точки пересечения с осями координат графика функции y=x²-9x+20.

x1=4; x2=5. График пересекает ось абсцисс в точках (4; 0) и (5; 0).

y=0²-9∙0+20=20. Отсюда, (0; 20) — точка пересечения параболы y=x²-9x+20 с осью ординат.

Пересечение с осями онлайн

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.

Найти точки пересечения функции с осями координат:

При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:

График данной функции представлен на рисунке:

Как следует из рисунка, наша функция пересекает ось в двух точках, а ось — в одной.

Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:

Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.

Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:

Таким образом, мы нашли точку пересечения нашей функции с осью ординат .

Другие полезные разделы:

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Как найти координаты точек пересечения графика функции: примеры решения

Вы будете перенаправлены на Автор24

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac<1> <2>– 2 = — 2frac12$.

Точка пересечения будет $(-frac<1><2>;- 2frac12)$.

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Второе уравнение проще первого, поэтому подставим его вместо $y$:

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — frac<1> <2>= frac<1><2>$.

Точки пересечения будут $(2;3)$ и $(-frac<1><2>; frac<1><2>)$.

Третий способ

Готовые работы на аналогичную тему

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 07.05.2021

источники:

http://mathforyou.net/online/calculus/intercepts/

http://spravochnick.ru/matematika/kak_nayti_koordinaty_tochek_peresecheniya_grafika_funkcii_primery_resheniya/

Источник

Загрузить PDF

В алгебре прямоугольную систему координат на плоскости образуют две взаимно перпендикулярные оси – ось Х (горизонтальная ось) и ось Y (вертикальная ось). Точки пересечения – это точки, в которых графики функций пересекают оси координат. Точка пересечения с осью Y и точка пересечения с осью X лежат на соответствующих осях. В простых задачах точку пересечения с осью Х легко найти по графику функции. Также эту точку пересечения можно вычислить с помощью уравнения функции.

1

Найдите ось Х. Прямоугольная система координат образуется двумя осями – осью Х (горизонтальная ось, которая направлена слева направо) и осью Y (вертикальная ось, которая направлена снизу вверх).^[1] Чтобы найти точку пересечения с осью Х, посмотрите на эту ось.
2

Найдите точку, в которой график пересекает ось Х. Это точка пересечения графика с осью Х.^[2] Если нужно найти точку пересечения с осью Х по графику, возможно, координатой этой точки будет целое число, например, 4. Однако в большинстве случаев по графику удастся определить только приблизительную координату , например, между 4 и 5.
3

Реклама

1
2
3
4

Реклама

1
Определите, записано ли уравнение в виде квадратного уравнения. Квадратное уравнение имеет вид $ax^{{2}}+bx+c=0$ .^[9] Квадратное уравнение имеет два корня: график такого уравнения представляет собой параболу и пересекает ось Х в двух точках.^[10]
- Например, уравнение $x^{{2}}+3x-10=0$ является квадратным уравнением, поэтому график пересечет ось Х в двух точках.
2

Запишите формулу для решения квадратного уравнения. Формула: $x={frac {-bpm {sqrt {b^{{2}}-4ac}}}{2a}}$ , где – коэффициент при переменной второго порядка ( $x^{{2}}$ ), – коэффициент при переменной первого порядка (), – свободный член.^[11]
3

Подставьте соответствующие значения в формулу для решения квадратного уравнения. Убедитесь, что вместо каждой переменной подставляете правильное значение.
4

Упростите уравнение. Для начала перемножьте соответствующие значения. Убедитесь, что учли все знаки «плюс» и «минус».
5

Возведите соответствующее значение в квадрат. Сделайте это со значением переменной . Затем результат прибавьте к другому числу, которое находится под знаком корня.
6

Выполните сложение. Так как в формуле присутствует знак , придется выполнить одну операцию сложения и одну операцию вычитания. Выполните сложение, чтобы найти первое значение .
7

Выполните вычитание. Так вы найдете второе значение . Сначала извлеките квадратный корень, потом выполните вычитание в числителе и, наконец, результат разделите на 2.
8

Реклама

Советы

Если дано линейное уравнение вида , нужно знать угловой коэффициент (он равен значению коэффициента k) и координату «у» точки пересечения прямой с осью Y (она равна значению коэффициента b). Вместо «у» подставьте 0 и найдите «х». Вы получите координату «х» точки пересечения прямой с осью Х.

Об этой статье

Эту страницу просматривали 75 804 раза.

Была ли эта статья полезной?

Источник

В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.

Как найти нули квадратичной функции

Запомните!

Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.

Рассмотрим задачу.

Найти нули квадратичной
функции «y = x² − 3».

Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.

0 = x² − 3
x² − 3 = 0

x_1;2 =

0 ±
√0² − 4 · 1 · (−3)

2 · 1

x_1;2 =

x_1;2 = ±√3

Ответ: нули функции «y = x² − 3» :

x₁ = √3;

x₂ = −√3 .

Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение

Запомните!

Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:

вместо «y» подставить в функцию заданное числовое значение;
решить полученное квадратное уравнение относительно «x».

Рассмотрим задачу.

При каких значениях «x» функция
«y = x² − x − 3» принимает значение
«−3».

Подставим в исходную функцию
«y = x² − x − 3» вместо «y = −3» и
найдем «x».

y = x² − x − 3

−3 = x² − x − 3
x² − x − 3 = −3
x² − x − 3 + 3 = 0
x² − x = 0
x_1;2 =

1 ±
√1² − 4 · 1 · 0

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 1	x₂ = 0

Ответ: при «x = 0» и
«x = 1» функция «y = x² − x − 3»
принимает значение «y = −3».

Как найти координаты точек пересечения параболы и прямой

Запомните!

Чтобы найти точки пересечения параболы с прямой нужно:

приравнять правые части функций (те части функций, в которых содержатся «x»);
решить полученное уравнение относительно «x»;
подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».

Рассмотрим задачу.

Найти координаты точек пересечения параболы «y = x²»
и прямой «y = 3 − 2x».

Приравняем правые части функций и решим
полученное уравнение относительно «x».

x² = 3 − 2x
x² − 3 + 2x = 0
x² + 2x − 3 = 0

x_1;2 =

−2 ±
√2² − 4 · 1 · (−3)

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 1	x₂ = −3

Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.

1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.

2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.

Запишем полученные точки пересечения с их координатами в ответ.

Ответ: точки пересечения параболы
«y = x²»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).

Как определить, принадлежит ли точка графику функции параболы

Запомните!

Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.

Если получится верное равенство, значит, точка принадлежит графику функции.
Если получится неверное равенство, значит, точка
не принадлежит графику функции.

Рассмотрим задачу:

Не строя графика функции «y = x²», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).

Подставим в функцию
«y = x²»

координаты точки (·) А(2; 6).

y = x²
6 = 2²
6 = 4

(неверно)

Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x²».

Подставим в функцию
«y = x²»

координаты точки (·) B(−1; 1).

y = x²
1 = (−)1²
1 = 1

(верно)

Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x²».

Как найти точки пересечения параболы с осями координат

Рассмотрим задачу

Найти координаты точек пересечения параболы
«y = x² −3x + 2» с осями координат.

Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:

Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x² −3x + 2»
и найдем их координаты по оси «Ox».

0 = x² −3x + 2
x² −3x + 2 = 0

x_1;2 =

3 ±
√3² − 4 · 1 · 2

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 2	x₂ = 1

Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).

Теперь найдем координаты точки пересечения с осью «Oy».

Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.

Подставим «x = 0»
в исходную функцию
«y = x² −3x + 2»
и найдем координату точки по оси
«Oy».

y(0) = 0² − 3 · 0 + 2 = 2

Выпишем координаты полученной точки: (·) C (0; 2)

Запишем в ответ все координаты точек пересечения параболы с осями.

Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).

Как определить при каких значениях x функция принимает
положительные или
отрицательные значения

Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.

Запомните!

Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:

провести прямые через точки в местах, где график пересекает ось «Ox»;
определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
записать ответ для каждого промежутка относительно «x».

Рассмотрим задачу.

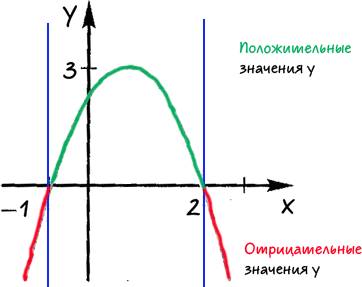
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.

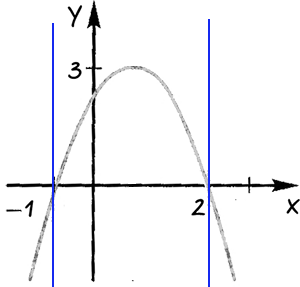
Проведем через точки, где график функции пересекает ось «Ox» прямые.

Определим области, где функция принимает отрицательные или положительные значения.

Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.

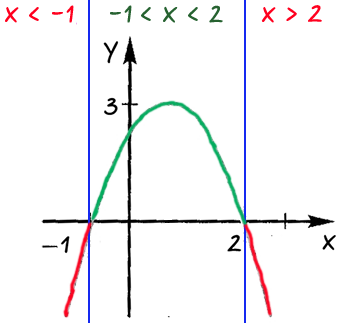
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Данный калькулятор предназначен для определения точек пересечения графика функции с осями координат.
В точке пересечения функции с осью Ox координата y всегда равна нулю, а в точке пересечения с осью Oy координата x=0.
Для того чтобы найти точки пересечения графика функции с осью ординат (Oy), необходимо подставить в уравнения функции x=0 , тем самым, найти y. Аналогично, чтобы найти точки пересечения графика функции с осью абсцисс (Ox), необходимо подставить в уравнение функции y=0 и найти x.

Нахождение координат точек пересечения функции с осями используется для анализа функции и построения ее графика.
Для того чтобы получить ответ, введите функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

Для получения полного хода решения нажимаем в ответе Step-by-step.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек
пересечения графика функции с осями координат.

График данной функции представлен на рисунке:

Как следует из рисунка, наша функция пересекает ось

в двух точках, а ось

— в одной.

Сначала найдём точки пересечения функции

с осью
. Сразу отметим, что в этих точках координата
. Поэтому для их поиска, нам нужно
решить уравнение:

Это
квадратное уравнение
имеет два корня:

Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс:

и
. Стоит отметить, что задача поиска пересечений функции с осью

эквивалентна задаче нахождения
нулей функции.

Теперь найдём точку пересечения с осью ординат. В этой точке координата
. Поэтому для их поиска, просто подставляем значение

в нашу функцию:

Таким образом, мы нашли точку пересечения нашей функции с осью ординат
.

Источник

Точки пересечения графика осями

Пересечение с осями онлайн

Другие полезные разделы:

Оставить свой комментарий:

Как найти координаты точек пересечения графика функции: примеры решения

Первый способ

Второй способ

Третий способ

Готовые работы на аналогичную тему

Советы

Об этой статье

Была ли эта статья полезной?

Как найти нули квадратичной функции

Как найти при каких значениях «x» квадратичная функция принимает заданное числовое значение

Как найти координаты точек пересечения параболы и прямой

Как определить, принадлежит ли точка графику функции параболы

Как найти точки пересечения параболы с осями координат

Как определить при каких значениях x функция принимает положительные или отрицательные значения

Ваши комментарии

Не пропустите также:

Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение

Как определить при каких значениях x функция принимает
положительные или
отрицательные значения