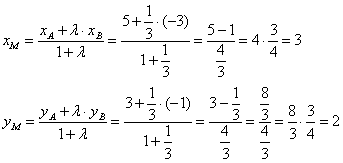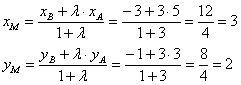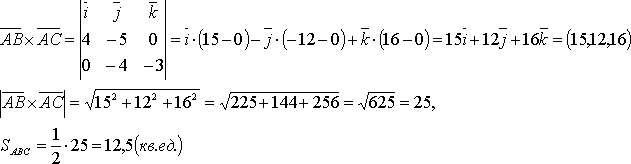Как найти координаты точки если известно отношение

1.5.6. Деление отрезка в данном отношении

Рассмотрим пару точек  (плоскости или

пространства) и отрезок :

Что будем с ним делать? На это раз пилить. Точкой :

В данном примере точка  делит отрезок  ТАКИМ образом, что отрезок  в два раза короче отрезка . ЕЩЁ можно сказать, что точка  делит отрезок  в отношении  («один к двум»), считая от вершины .

На сухом математическом языке этот факт записывают пропорцией   или чаще в виде привычной дроби: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном

случае: .

Пропорцию можно составить и в другом порядке:  –

сия запись означает, что отрезок  в два раза

длиннее отрезка , но какого-то принципиального

значения для решения задач это не имеет. Можно так, а можно так.

Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: . Если составить

пропорцию наоборот, тогда получаем: .

Формулы деления отрезка в данном отношении:

Если известны две точки плоскости , то

координаты точки , которая делит отрезок  в отношении , выражаются формулами:

В пространственном случае  и  добавляется дополнительная координата:
.

Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы выводятся с помощью векторов (куда ж теперь

без них? =)).

Задача 11

Найти координаты точки , делящей отрезок  в отношении , если известны точки

Решение: по умолчанию, отсчёт начинается от первого конца отрезка: . По формулам деления отрезка в данном отношении, найдём точку :

Ответ:

Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате

чего часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от

многоэтажности дроби (см. Приложение Школьные материалы) и проводим окончательные

упрощения.

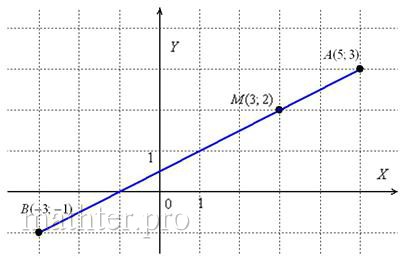
В задаче не требуется строить чертежа, но его полезно выполнить на черновике:

– чтобы убедиться в том, что соотношение  действительно выполнено, то есть отрезок  в три раза короче отрезка . Если длины не очевидны, то отрезки всегда можно тупо измерить обычной

линейкой.

Существует и второй способ решения: в нём отсчёт начинается с точки  и справедливым является отношение:  (иными словами, отрезок  в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:

Ответ:

Заметьте, что в формулах необходимо переместить координаты точки  на первое место, поскольку маленький триллер начинался именно с неё. Также видно, что

второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке.

Так, если по условию дан отрезок , то

предполагается, что вы составите пропорцию ,

если дан отрезок , то «негласно» подразумевается

пропорция , и так далее.

Задача 12

а) Точка  принадлежит отрезку . Известно, что отрезок  в два раза длиннее отрезка . Найти точку ,

если . Выполнить проверку.
б) Даны точки . Найти точку , делящую отрезок  в отношении .

Удачного распила!

1.5.7. Формулы координат середины отрезка

1.5.5. Как найти единичный вектор?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Деление отрезка в заданном соотношении: координаты точки

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

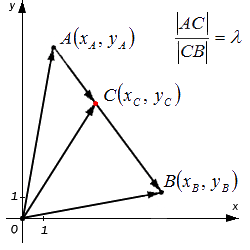
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Деление векторов в данном соотношении

Пусть вектор 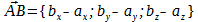задан координатами своего начала A(a_x; a_y; a_z) и конца B(b_x; b_y; b_z) и пусть точка C(c_x; c_y; c_z) расположена между точка A и B

пусть при этом известно соотношение длин векторов

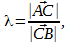
тогда координаты точки C(c_x; c_y; c_z) находятся по формулам

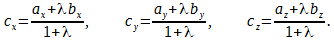
Примеры решения заданий по делению векторов и отрезков

Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.

Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении

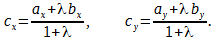
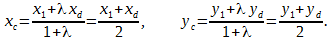
Подставим в последнее равенство координаты x_c, y_c, x_d, y_d:

3 = (x1 + 5)/2, 4 = (y1 + 6)/2,

откуда находим, x₁ = 1, y₁ = 2. Точка A имеет координаты A(1, 2).

Поскольку точка D есть середина отрезка CB, то x_d = (x_c + x₂)/2, или 5 = (3 + x₂)/2, отсюда x₂ = 7.

отсюда y₂ = 8. Получили B(7, 8).

О т в е т: A(1, 2), B(7, 8).

Даны вершины треугольника A(2, -4), B(4, -5) и C(-4, 7). Определить середины его сторон.

Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:

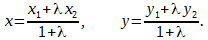
Поскольку отрезки делятся на равные части, то

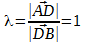
Тогда формула приобретает вид:

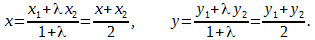
Координата x для отрезка AB равна (2+4)/2 = 3, координата y для отрезка AB равна (-4-5)/2 = -4,5.

Координата x для отрезка AC равна (2-4)/2 = -1, координата y для отрезка AC равна (-4+7)/2 = 1,5.

Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.

О т в е т: искомые точки имеют координаты (3; -4,5), (-1; 1,5) и (0; 1).

Даны три вершины параллелограмма A(2, -4), B(4, -2), C(-2, 4). Определить четвёртую вершину D, противоположную B.

Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.

Назовём точку пересечения диагоналей точкой E.

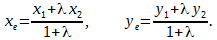
Поскольку этой точкой диагонали делятся на два равных отрезка

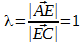
то формула приобретает вид:

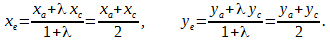
Найдём середину отрезка AC:

Итак, точка E имеет координаты (0, 0).

Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда

подставим известные значения:

Теперь найдём вторую координату:

подставим известные значения:

Даны вершины треугольника A(2, 3); B(4, -10); C(-4, 1), определить длину его медианы, проведённой из вершины B.

Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:

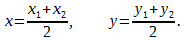
Точка D имеет координаты (-1, 2).

Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:

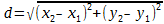
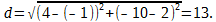
О т в е т: Длина медианы, проведённой из вершины B, равна 13.

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Высшая математика.
• Аналитическая геометрия.
• Деление отрезка в заданном отношении (векторный и координатный способы).

Деление отрезка в заданном отношении (векторный и координатный способы).

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $overline=r_1,$ $overline=r_2,$ $overline=r.$ Так как, $$overline=r-r_1, overline=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambdaneq -1$) $$r=frac<1+lambda>.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac<1+lambda>, y=frac<1+lambda>, z=frac<1+lambda>.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac=frac<1><2>;$$ $$x_C=frac<1+lambda_1>=frac<3+frac<1><2>cdot 6><1+frac<1><2>>=4;$$

Далее находим координаты точки $D:$

Ответ: $(4, 0)$ и $(5, 2).$

2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

Аналогичные равенства запишем для точки $D:$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$

Вывод формул для нахождения координат точки, делящей отрезок в данном отношении, на плоскости.

Начнем
с постановки задачи на плоскости.

Пусть
на плоскости введена прямоугольная
декартова система координат Oxy и
заданы координаты двух несовпадающих
точек и .
Нам требуется найти координаты и точки С,
которая делит отрезок АВ в
отношении ,
где —
некоторое положительное действительное
число.

Поясним
смысл фразы: «точка С делит
отрезок АВ в
отношении ».
Это выражение означает, что точка С лежит
на отрезке АВ (является
внутренней точкой отрезка АВ)
и отношение длин отрезков АС и СВ равно (то
есть, выполняется равенство ).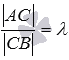
Обратите внимание, что в этом случае
точка А является
как бы началом отрезка, а точка В –
его концом. Если же сказано, что
точка С делит
отрезок ВА (а
не АВ)
в отношении ,
то будет выполняться равенство .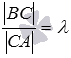
Очевидно, что при точка С является
серединой отрезка АВ.

Поставленная
задача может быть решена с помощью
векторов.

Изобразим
в прямоугольной декартовой системе
координат некоторый отрезок АВ,
точку С на
нем и построим радиус-векторы
точек А, В и С,
а также векторы и .
Будем считать, что точка С делит
отрезок АВ в
отношении .

Мы
знаем, что координаты
радиус-вектора точки
равны соответствующим координатам этой
точки, поэтому, и .
Найдем координаты вектора ,
которые будут равны искомым координатам
точки С,
делящей отрезок АВ в
заданном отношении .

В
силу операции
сложения векторов можно
записать равенства и .
Их мы используем в следующем абзаце.

Так
как точка С делит
отрезок АВ в
соотношении ,
то ,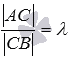
откуда .
Векторы и лежат
на одной прямой и имеют одинаковое
направление, а выше мы отметили, что ,
поэтому, по определению
операции умножения вектора на числосправедливо равенство .
Подставив в него ,
имеем .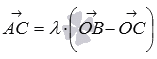
Тогда равенство можно
переписать как ,
откуда в силу свойств
операций над векторами получаем .

Осталось
вычислить координаты вектора ,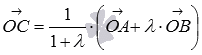
выполнив необходимые операции
над векторами  и  в
координатах.
Так как и ,
то ,
следовательно, .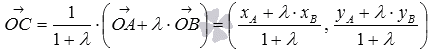

Таким
образом, на плоскости координаты
точки С,
которая делит отрезок АВ в
отношении ,
находятся по формулам 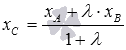и .

15. Векторное произведение векторов.

 Векторное
проведение векторов.

Определение:
Под векторным произведением двух
векторов  и  понимается
вектор,  для
которого:

-модуль
равен площади параллелограмма,
построенного на данных векторах, т.е. ,
где угол
между векторами  и 

-этот
вектор перпендикулярен перемножаемым
векторам, т.е. 

-если
векторы  неколлинеарны,
то они образуют правую тройку векторов.

 Свойства
векторного произведения:

1.При
изменении порядка сомножителей векторное
произведение меняет свой знак на
обратный, сохраняя модуль, т.е. 

2.Векторный
квадрат равен нуль-вектору, т.е. 

3.Скалярный
множитель можно выносить за знак
векторного произведения, т.е. 

4.Для
любых трех векторов   справедливо
равенство 

5.Необходимое
и достаточное условие коллинеарности
двух векторов  и : 

 Векторное
произведение в координатной форме.

 Если
известны координаты векторов  и , то
их векторное произведение находится
по формуле:

  .

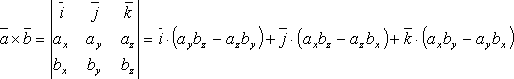
 Тогда
из определения векторного произведения
следует, что площадь параллелограмма,
построенного на векторах  и ,
вычисляется по формуле:

Пример: Вычислить
площадь треугольника с
вершинами (1;-1;2), (5;-6;2), (1;3;-1).

Решение: .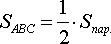

, ,
тогда площадь треугольника АВС будет
вычисляться следующим образом:

 ,

Соседние файлы в предмете Алгебра и геометрия

• #
• #
• #
• #