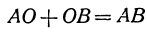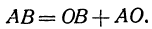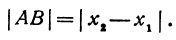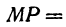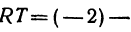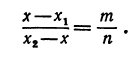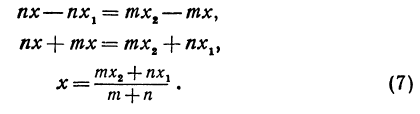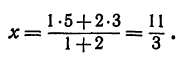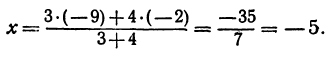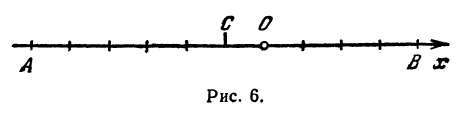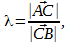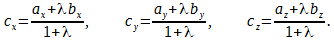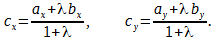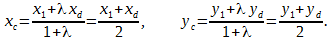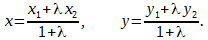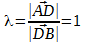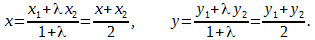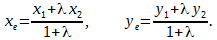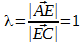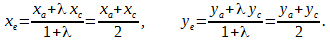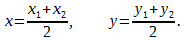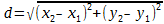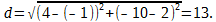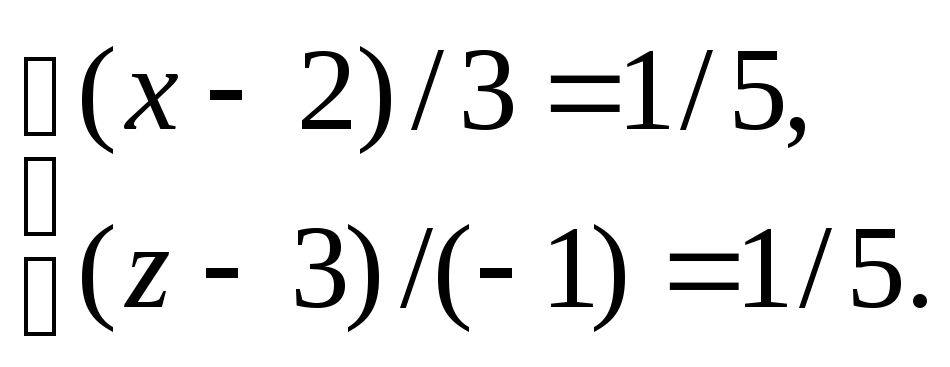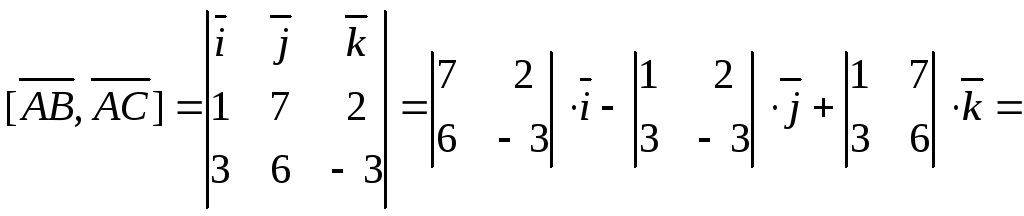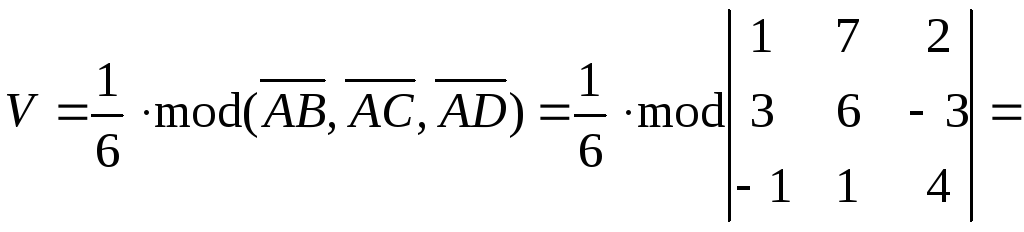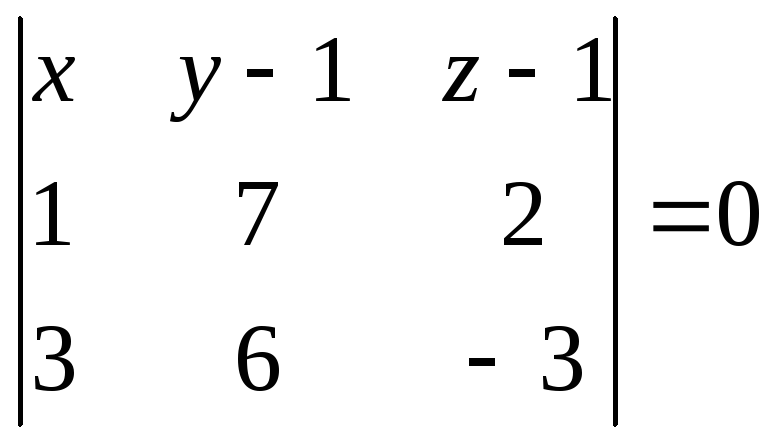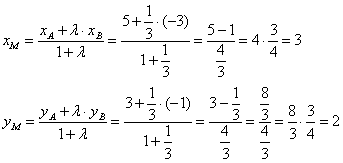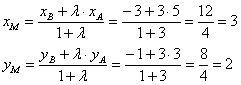Как найти координаты точки делящей отрезок пополам - AvtoShod.ru

Координаты на прямой:

Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).

Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.

Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.

Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.

Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:

Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.

Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.

Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:

(рис. 2 и 3).

Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.

Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать

(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или

Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)

поэтому можно написать

Получен следующий результат:

Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.

Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:

Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.

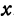
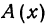
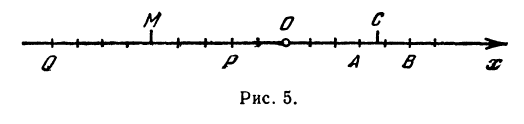
Точку А, имеющую координатной число , будем обозначать .

Указанные на рис. 4 точки имеют следующие координаты: 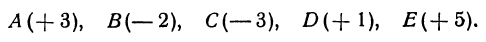Будем также писать

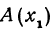
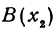
Если даны точки и , то на основании формул (3) и (4) получим

т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.

Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:

Заказать решение задач по высшей математике

Пример:

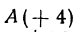
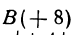
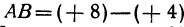
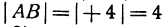
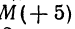
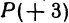
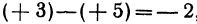
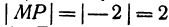
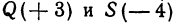
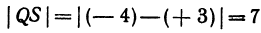
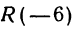
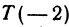
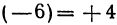
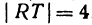
Если даны точки ,, то отрезок , а его длина . Если даны точки и , то отрезок , а его длина . Даны две точки: . Длина отрезка . Даны две точки и ; отрезок , а его длина | .

Пример:

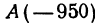
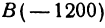
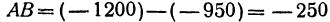
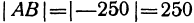
Начало отрезка АВ находится в точке , а конец—в точке ; найти его направление и длину. Отрезок . Так как он получился отрицательным, то его направление противоположно направлению оси. Его длина равна .

Пример:

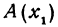
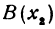
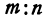
На координатной оси даны две точки: и . Найти точку С, лежащую между ними и делящую отрезок АВ в отношении . Чтобы найти точку, надо найти ее координату. По условию задачи должно быть

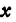
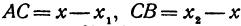
Обозначая координату искомой точки С через и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что . Подставляя эти выражения в равенство (6), будем иметь

Решая последнее уравнение относительно 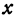, найдем:

Это и есть координата искомой точки.

Пример:

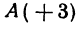
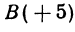
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка и конец (рис. 5).

Решение:

Здесь 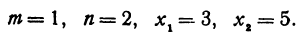Применяя формулу (7), получим

Пример:

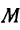
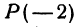
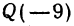
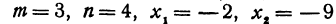
Найти точку , делящую расстояние между точками и в отношении 3:4 (рис. 5). Здесь . По формуле (7) находим

Решение:

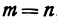
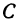
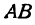
Если , т. е. точка делит отрезок пополам, тогда формула (7) перепишется так:

Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.

Пример:

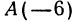
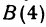
Найдем середину отрезка, заключенного между точками и (рис.6).

Решение:

Применяя формулу (8), получим,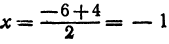

Координаты на плоскости
Линейная функция
Квадратичная функция
Тригонометрические функции
Элементы матричного анализа
Уравнение линии
Функции нескольких переменных
Комплексные числ

Источник

Деление отрезка в заданном соотношении: координаты точки

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

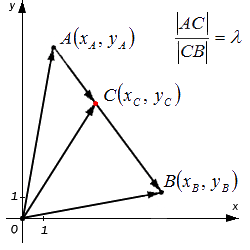
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Деление вектора данном отношении

Деление векторов в данном соотношении

Пусть вектор 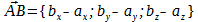задан координатами своего начала A(a_x; a_y; a_z) и конца B(b_x; b_y; b_z) и пусть точка C(c_x; c_y; c_z) расположена между точка A и B

пусть при этом известно соотношение длин векторов

тогда координаты точки C(c_x; c_y; c_z) находятся по формулам

Примеры решения заданий по делению векторов и отрезков

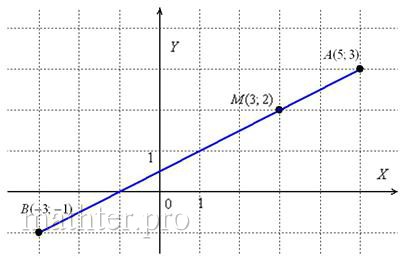
Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.

Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении

Подставим в последнее равенство координаты x_c, y_c, x_d, y_d:

3 = (x1 + 5)/2, 4 = (y1 + 6)/2,

откуда находим, x₁ = 1, y₁ = 2. Точка A имеет координаты A(1, 2).

Поскольку точка D есть середина отрезка CB, то x_d = (x_c + x₂)/2, или 5 = (3 + x₂)/2, отсюда x₂ = 7.

отсюда y₂ = 8. Получили B(7, 8).

О т в е т: A(1, 2), B(7, 8).

Даны вершины треугольника A(2, -4), B(4, -5) и C(-4, 7). Определить середины его сторон.

Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:

Поскольку отрезки делятся на равные части, то

Тогда формула приобретает вид:

Координата x для отрезка AB равна (2+4)/2 = 3, координата y для отрезка AB равна (-4-5)/2 = -4,5.

Координата x для отрезка AC равна (2-4)/2 = -1, координата y для отрезка AC равна (-4+7)/2 = 1,5.

Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.

О т в е т: искомые точки имеют координаты (3; -4,5), (-1; 1,5) и (0; 1).

Даны три вершины параллелограмма A(2, -4), B(4, -2), C(-2, 4). Определить четвёртую вершину D, противоположную B.

Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.

Назовём точку пересечения диагоналей точкой E.

Поскольку этой точкой диагонали делятся на два равных отрезка

то формула приобретает вид:

Найдём середину отрезка AC:

Итак, точка E имеет координаты (0, 0).

Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда

подставим известные значения:

Теперь найдём вторую координату:

подставим известные значения:

Даны вершины треугольника A(2, 3); B(4, -10); C(-4, 1), определить длину его медианы, проведённой из вершины B.

Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:

Точка D имеет координаты (-1, 2).

Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:

О т в е т: Длина медианы, проведённой из вершины B, равна 13.

Деление отрезка в заданном соотношении: координаты точки

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Лекция Способы задания векторов. Деление отрезка в заданном отношении. Скалярное произведение двух векторов и его основные свойства.

1.4. Способы задания векторов

Вектор может быть задан следующими способами:

1. Координатами вектора

2 . Координатами начальной z

и конечной точек.

3. Модулем вектора и углами , M

которые он образует с координатными осями.

При этом значения

называются направляющими косинусами . O y

Между этими способами задания a _z

векторов существует определённая связь. a _x

Например, переход от (2) к (1) x a _y

осуществляется следующим образом :

т ак как , то z A

Переход от (3) к (1) и наоборот

осуществляется по формулам: B

x O y

1.5. Деление отрезка в заданном отношении

Р ассмотрим следующую задачу : даны две точки и . Требуется найти точку такую, что отно-шение z А

Построим векторы : М

Из условия коллинеарности векторов

и имеем В

Полученное равенство представим в

координатной форме х Оу

(1)

Замечание 1. Из формул (1) следует частный случай деления отрезка пополам

П ример 1. Треугольник задан координатами своих вершин Найти его центр тяжести . z В

Известно, что центр тяжести треугольника

лежит на пересечении его медиан и, если

точка К  середина стороны ВС , то по А М К

свойству медиан у

Определим вначале координаты х С

точки К :

далее по формулам (1) получим координаты точки М :

Тема 2: Скалярное произведение

2.1. Скалярное произведение двух векторов и его основные свойства

Определение. Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается

(2)

Замечание 2. Формулу (2) можно представить в другой форме

(3)

Рассмотрим механический смысл скалярного произведения. Если  постоянная сила, а  вектор перемещения, то  работа силы на перемещении

Из определения скалярного произведения следуют его свойства:

1.  скалярное произведение коммутативно.

2. , если векторы и перпендикулярны (ортогональны), или хотя бы один из них является нулевым вектором.

Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:

Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.

2.2. Скалярное произведение векторов, заданных координатами

Из определения и свойства (1) скалярного произведения следуют формулы : .

Аналогично получаем :

(4)

2.3. Длина вектора. Угол между двумя векторами.

По формулам (2) и (4) получаем

(5)

Из определения скалярного произведения и формул (4), (5) следует

(6)

(7)

Если в формуле (7) положить , то найдем

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов

; . (8)

Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.

Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство

Пример 2. Даны два вектора Найти их скалярное произведение и угол между ними.

По формулам (5) и (7) получаем

Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору и образует угол с вектором

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора равны значениям соответствующих направляющих косинусов и поэтому из условия задачи получаем следующую систему уравнений

Из второго уравнения системы получаем Тогда из первого уравнения имеем . Если полученные выражения подставить в третье уравнение системы, то приходим к квадратному уравнению

Из этого уравнения и . Тогда окончательно нахо-дим два единичных вектора , удовлетворяющих условию задачи.

Деление отрезка в данном отношении в пространстве

Данные уравнения получаются следующим образом

Требуется найти координаты точки A₀(x₀, y₀,z₀), делящей отрезок в отношении λ, т.е.

Отсюда получаем исходные уравнения, т.е.

Деление отрезка в данном отношении на плоскости см. здесь

Рассмотрим ещё один из способов деления отрезка в данном отношении в пространстве.

где r₁ и r₂ — радиус-вектор точек А₁ и А₂

Координаты точки A₀ находятся по формулам

Координаты середины отрезка в пространстве

В частности координаты середины отрезка А₁А₂ в пространстве определяются уравнениями:

Найти координаты точки А, делящей отрезок А₁А₂ в отношении А₁А:АА₂=2:3, если A₁ <3; 4; -2>и A₂

источники:

http://b4.cooksy.ru/articles/delenie-vektora-dannom-otnoshenii

Деление отрезка в данном отношении в пространстве

Источник

Деление отрезка в данном отношении

Пусть даны точки

и
.
Требу-ется
найти координаты точки
,
делящей отрезок прямой, заключенный
между М₁
и М₂,
в отношении
,

(рис. 7.6).

Рис. 7.6

Рассмотрим
векторы

и
.
Они коллинеарны и одинаково направлены,
то есть могут отли-чаться только длиной.
По условию

поэтому

или
в координатной форме

Из
равенства этих двух векторов следует
равенство их соот-ветствующих координат:

,
,

Отсюда

,
,
,

В частности, если
точка М
делит отрезок М₁М₂
пополам, то

и
,
,
,
то есть координаты
точки, делящей отрезок пополам, равны
полусуммам соответствующих координат
концов отрезка.

Пример 7.12.
Найти
координаты точки М,
делящей по-полам отрезок прямой
,
заключенный между плоскостями
Oxz
и Оxу.

Решение.
Найдем точку пересечения прямой с
плоскостью
Oxz,
полагая в
уравнениях прямой
.
Тогда получим

или

Из
последней системы находим
,
.
Эти коор-динаты вместе с

определяют точку

Анало-гично, полагая в уравнениях прямой
,
имеем:

или

откуда
,
.
Получим
точку

пересечения прямой с плоскостью Оxу.
Зная
координаты концов

и

отрезка АВ,
по формулам деления отрезка пополам
определим координаты
точки М
– середины отрезка АВ:
;
;

Итак,

–
искомая
точка.

Пример
7.13.
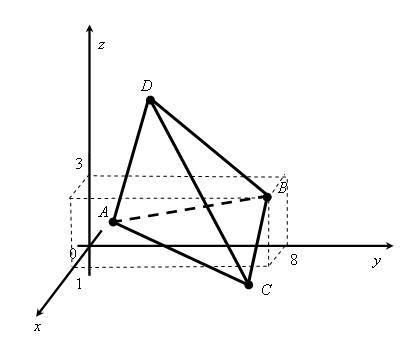
Даны координаты вершин пирамиды
,
,
,
.
Найти: 1) длины ребер АВ
и AC;
2) угол между ребрами АВ
и АС;
3) площадь грани АВС;
4) объем пирамиды ABCD;
5) уравнение прямой АВ;
6) уравнение плоскости АВС;
7) уравнение высоты пирамиды, опущенной
на грань АВС.
Сделать чертеж.

Решение

Длина
ребра AB
совпадает с длиной вектора
,
поэтому определим координаты векторов

и

Длина
вектора равна корню квадратному из
суммы квадратов его координат, то есть

Угол
между ребрами AB
и AC
совпадает с углом между векторами

и
,
который можно определить по формуле:

,
.

Грань
ABC
представляет собой треугольник, его
пло-щадь найдем через векторное
произведение:

так
как

Объем
пирамиды вычислим по формуле:

Здесь

Уравнение
прямой, проходящей через точки А,
В,
имеет вид:

,
то есть
.

Уравнение
плоскости ABC
определим из равенства

,

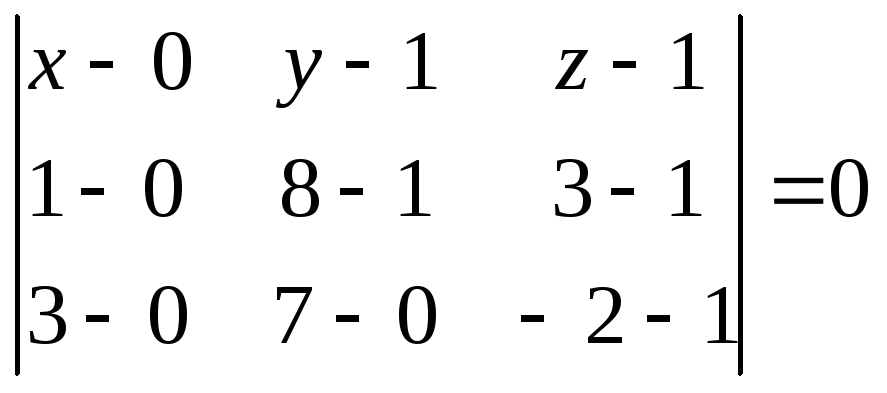
или

Так
как высота – это прямая, перпендикулярная
плос-кости ABC,
ее направляющим вектором будет
вектор-нормаль

плоскости
ABC,
тогда уравнение высоты имеет вид:

Выполним
чертеж (рис. 7.5).

Рис. 7.5

Тема 8. Функции. Теория пределов Понятие функции

В теме 5 мы уже
встречались с понятием функции, информация
о которой основывалась на материале из
школьного курса математики. Здесь это
понятие получит свое дальнейшее развитие.

Пусть на действительной
оси R
заданы два числовых множества

и
.

Определение.
Будем говорить, что на множестве X
задана функция
f
действительной переменной x,
если известен закон (отображение), по
которому каждому значению

по закону f
ставится в соответствие единственное
значение

и обозначается
.
Переменная x
называется аргументом функции f,
множество X
– областью определения функции,
переменная y
– значением функции или зависимой
переменной, а множество Y
– областью значений функции.

Замечание.
Область Y
значений функции обычно не указыва-ется,
так как множество принимаемых значений
функции определяет сам закон.

Допускаются
многозначные функции (то есть одному x
соответствует более одного значения
y).
Обычно эти случаи оговариваются особо.

Замечание.
Для обозначения функциональной
зависимос-ти вместо символа функции f
можно использовать любую дру-гую букву
(но не число) любого алфавита.

Определение.
Совокупность всех значений независимой
переменной х,
для которых функция

определена, назы-вается областью
определения,
или областью существования функции, и
обозначается
.

Определение.
Пусть задана функция
.
Тогда

называется значением
этой функции при

Пример 8.1.
Найти значения

функции
.

Решение.
Вычислим значения функции при заданных
значениях аргумента
;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

1.5.6. Деление отрезка в данном отношении

Рассмотрим пару точек (плоскости или

пространства) и отрезок :

Что будем с ним делать? На это раз пилить. Точкой :

В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .

На сухом математическом языке этот факт записывают пропорцией или чаще в виде привычной дроби: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном

случае: .

Пропорцию можно составить и в другом порядке: –

сия запись означает, что отрезок в два раза

длиннее отрезка , но какого-то принципиального

значения для решения задач это не имеет. Можно так, а можно так.

Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: . Если составить

пропорцию наоборот, тогда получаем: .

Формулы деления отрезка в данном отношении:

Если известны две точки плоскости , то

координаты точки , которая делит отрезок в отношении , выражаются формулами:

В пространственном случае и добавляется дополнительная координата:
.

Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы выводятся с помощью векторов (куда ж теперь

без них? =)).

Задача 11

Найти координаты точки , делящей отрезок в отношении , если известны точки

Решение: по умолчанию, отсчёт начинается от первого конца отрезка: . По формулам деления отрезка в данном отношении, найдём точку :

Ответ:

Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате

чего часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от

многоэтажности дроби (см. Приложение Школьные материалы) и проводим окончательные

упрощения.

В задаче не требуется строить чертежа, но его полезно выполнить на черновике:

– чтобы убедиться в том, что соотношение действительно выполнено, то есть отрезок в три раза короче отрезка . Если длины не очевидны, то отрезки всегда можно тупо измерить обычной

линейкой.

Существует и второй способ решения: в нём отсчёт начинается с точки и справедливым является отношение: (иными словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:

Ответ:

Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё. Также видно, что