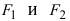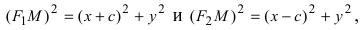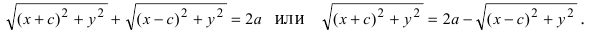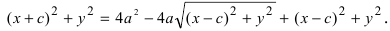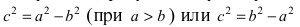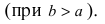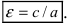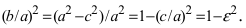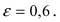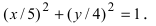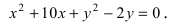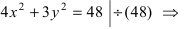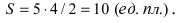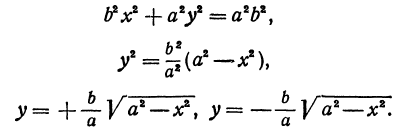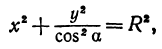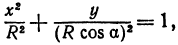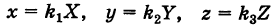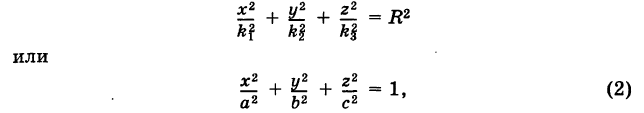Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Маркеры кликабельны и таскабельны.
Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx
Эллипс:
a:
b:
Углы (град.):
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
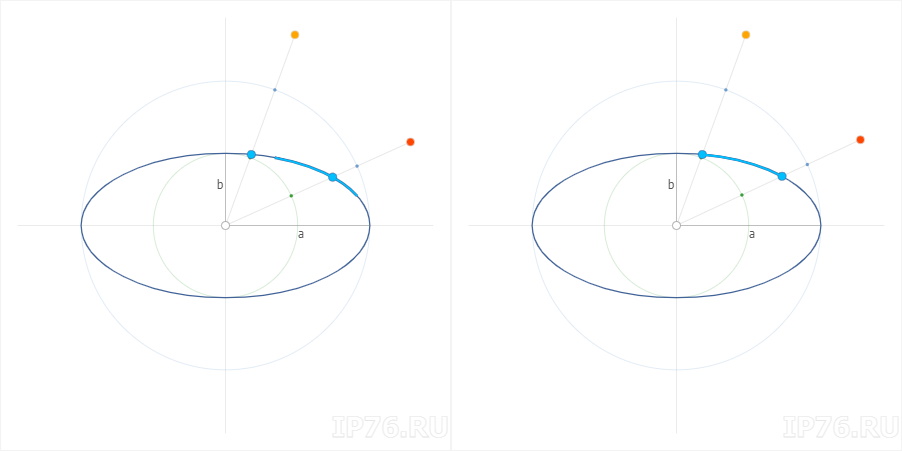
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
|
//— находим параметр (некий угол) для уравнения — SinCos(Angle,sn,cs); t := ArcTan2(a*sn, b*cs); |
Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.
О параметре
Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.
В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var t1 = start; var t2 = finish; ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.
Перепишем функцию с учетом нахождения параметра:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var sn = Math.sin(start); var cs = Math.cos(start); var t1 = Math.atan2(a*sn, b*cs); sn = Math.sin(finish); cs = Math.cos(finish); var t2 = Math.atan2(a*sn, b*cs); ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке справа видим, что все встало на свои места. Идеальная дуга )
Координаты точки наклонного эллипса
Перенесено в отдельную статью.
Практика
Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.
|
//****************************************************************** // Найти угол, который будет использован в расчете точки на элипсе // Т.е. тот самый параметр t в параметрическом уравнении эллипса: // x = a * cos t // y = b * sin t //****************************************************************** function GetEllipseAngleParam(ARect : TRectF; Angle : Extended) : Extended; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y begin a := ARect.Width/2; b := ARect.Height/2; SinCos(Angle,sn,cs); result := ArcTan2(a * sn, b * cs); end; |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//******************************************************************** // Найти координату точки на эллипсе по углу отклонения //******************************************************************** function CalcEllipsePointCoord(ARect : TRectF; Angle : extended) : TPointF; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y cnt : TPointF; // центр t : Extended; // параметр для уравнения эллипса begin // инициализация полуосей a := ARect.Width/2; b := ARect.Height/2; // центр эллипса cnt := ARect.CenterPoint; // находим параметр (некий угол) для уравнения SinCos(Angle,sn,cs); t := ArcTan2(a * sn, b * cs); // считаем результат по параметрическому уравнению SinCos (t, sn, cs); result.X := cnt.x + a * cs; result.Y := cnt.Y + b * sn; end; |
Скачать исходник + исполнямый файл
Друзья, спасибо за внимание!
Надеюсь, материал после правок стал понятней.
Подписывайтесь на телегу.
Если есть вопросы, с удовольствием отвечу )
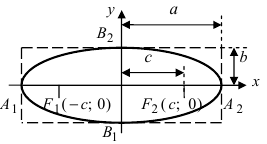
Эллипс: определение, свойства, построение
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек , и
есть величина постоянная
, бо́льшая расстояния
между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса.
Фокальное свойство эллипса
Точки , и
называются фокусами эллипса, расстояние между ними
— фокусным расстоянием, середина
отрезка
— центром эллипса, число
— длиной большой оси эллипса (соответственно, число
— большой полуосью эллипса). Отрезки
и
, соединяющие произвольную точку
эллипса с его фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
Отношение называется эксцентриситетом эллипса. Из определения
следует, что
. При
, т.е. при
, фокусы
и
, а также центр
совпадают, и эллипс является окружностью радиуса
(рис.3.36,6).
Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:
(3.49)
Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов . Для произвольной точки
, принадлежащей эллипсу, имеем:
Записывая это равенство в координатной форме, получаем:
Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:
Разделив на 4, возводим обе части уравнения в квадрат:
Обозначив , получаем
. Разделив обе части на
, приходим к каноническому уравнению эллипса:
Следовательно, выбранная система координат является канонической.
Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку . В этом случае канонической будет любая прямоугольная система координат с началом в точке
, a уравнение
является уравнением окружности с центром в точке
и радиусом, равным
.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.
Директориальное свойство эллипса
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При
, когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство эллипса). Здесь
и
— один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е.
или
.
В самом деле, например, для фокуса и директрисы
(рис.3.37,6) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса
и директрисы
.
Уравнение эллипса в полярной системе координат
Уравнение эллипса в полярной системе координат (рис.3.37,в и 3.37(2)) имеет вид
где фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус эллипса, а в качестве полярной оси — луч
(рис.3.37,в). Тогда для произвольной точки
, согласно геометрическому определению (фокальному свойству) эллипса, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение эллипса имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замену
:
что и требовалось доказать.
Геометрический смысл коэффициентов в уравнении эллипса
Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение , находим точки пересечения эллипса с осью абсцисс (с фокальной осью):
. Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна
. Этот отрезок, как отмечено выше, называется большой осью эллипса, а число
— большой полуосью эллипса. Подставляя
, получаем
. Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна
. Этот отрезок называется малой осью эллипса, а число
— малой полуосью эллипса.
Действительно, , причем равенство
получается только в случае
, когда эллипс является окружностью. Отношение
называется коэффициентом сжатия эллипса.
Замечания 3.9
1. Прямые ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).
2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.
Действительно, пусть в прямоугольной системе координат уравнение окружности имеет вид
. При сжатии к оси абсцисс с коэффициентом
координаты произвольной точки
, принадлежащей окружности, изменяются по закону
Подставляя в уравнение окружности и
, получаем уравнение для координат образа
точки
:
поскольку . Это каноническое уравнение эллипса.
3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.
Действительно, если точка принадлежит эллипсу
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат тому же эллипсу.
4. Из уравнения эллипса в полярной системе координат (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше
, тем эллипс более вытянут, а чем ближе
к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что
и
, получаем
где — коэффициент сжатия эллипса,
. Следовательно,
. Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия
и больше эксцентриситет. Для окружности
и
.
6. Уравнение при
определяет эллипс, фокусы которого расположены на оси
(рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет эллипс с центром в точке
, оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
При уравнение
описывает окружность радиуса
с центром в точке
.
Параметрическое уравнение эллипса
Параметрическое уравнение эллипса в канонической системе координат имеет вид
Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству .
Пример 3.20. Изобразить эллипс в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — большая полуось,
— малая полуось эллипса. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя
в уравнение эллипса, получаем
Следовательно, точки с координатами — принадлежат эллипсу.
Вычисляем коэффициент сжатия ; фокусное расстояние
; эксцентриситет
; фокальный параметр
. Составляем уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Координаты точки эллипса по углу
IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
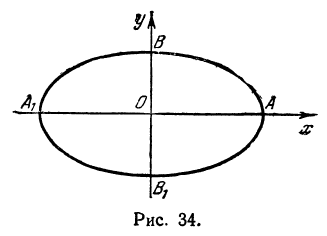
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства — вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b — малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
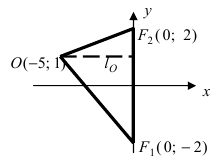
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина — в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
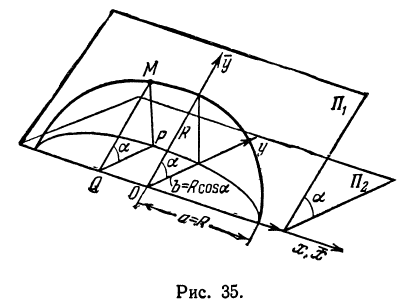
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://function-x.ru/curves_ellipse.html
http://www.evkova.org/ellips
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 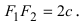
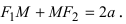
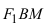
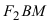
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 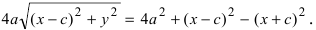
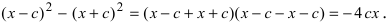
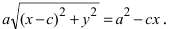
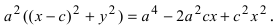
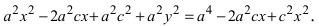
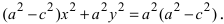
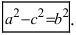
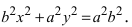
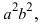
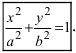
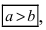
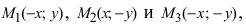
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 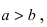
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 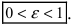
Если 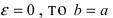
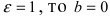
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 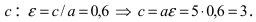
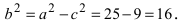
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 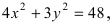
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
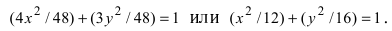
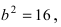
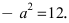
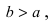
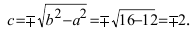
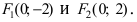
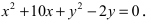
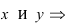
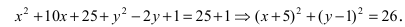
Построим в декартовой системе координат треугольник 
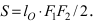
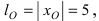
Эллипс в высшей математике
Рассмотрим уравнение
где 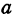
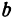
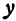
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 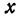
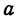
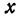
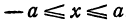
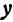
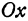
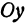
При 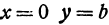
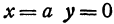
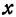

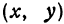
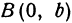
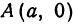
Полученная линия называется эллипсом. Число 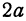
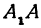
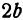
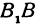
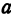
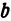
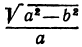
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 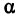
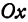
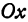
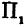
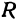
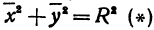
Пусть точка 
Обозначим проекцию точки 
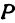
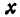
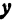
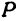

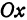
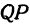
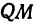
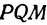
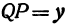
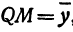
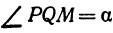
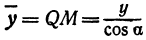

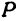
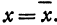
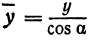
или
а это есть уравнение эллипса с полуосями 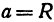
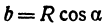
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 
(рис. 206). Отсюда
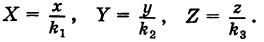
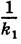
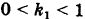
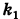
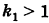
Подставляя эти формулы в уравнение (1), будем иметь
где 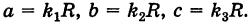
Величины 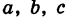
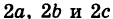
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
-
Определение эллипса.
Начать изучение
-
Фокусы, эксценриситет и директрисы эллипса.
Начать изучение
-
Уравнение касательной к эллипсу.
Начать изучение
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1label{ref1}
$$
при условии (a geq b > 0).
Из уравнения eqref{ref1} следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_{1}), (M_{2}) и (M_{3}) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Утверждение 1.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^{2}+y^{2}=a^{2}). При каждом (x) таком, что (|x| < a), найдутся две точки эллипса с ординатами (pm b sqrt{1-x^{2}/a^{2}}) и две точки окружности с ординатами (pm a sqrt{1-x^{2}/a^{2}}). Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно (b/a). Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении (b/a) (рис. 8.2).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Определение.
Пусть по определению
$$
c^{2}=a^{2}-b^{2}label{ref2}
$$
и (c geq 0).
Фокусами называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Определение.
Отношение
$$
varepsilon=frac{c}{a}label{ref3}
$$
называется эксцентриситетом эллипса.
Отметим, что (varepsilon < 1).
Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=a-varepsilon x, r_{2}=|F_{2}M|=a+varepsilon x.label{ref4}
$$
Доказательство.
Очевидно, что (r_{1}^{2}=(x-c)^{2}+y^{2}). Подставим сюда выражение для (y^{2}), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-frac{b^{2}x^{2}}{a^{2}}.nonumber
$$
Учитывая равенство eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+frac{c^{2}x^{2}}{a^{2}}=(a-varepsilon x)^{2}.nonumber
$$
Так как (x leq a) и (varepsilon < 1), отсюда следует, что справедливо первое из равенств eqref{ref4}: (r_{1}=a-varepsilon x). Второе равенство доказывается аналогично.
Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Доказательство.
Необходимость. Если мы сложим равенства eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.label{ref5}
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref{ref5}, то есть
$$
sqrt{(x-c)^{2}+y^{2}}=2a-sqrt{(x+c)^{2}+y^{2}}.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=asqrt{(x+c)^{2}+y^{2}}.label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref{ref2}. Мы придем к (b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}), равносильному уравнению эллипса eqref{ref1}.
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=frac{a}{varepsilon},\ x=-frac{a}{varepsilon}.label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.
Утверждение 4.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Доказательство.
Докажем это предложение для фокуса (F_{2}(-c, 0)). Пусть (M(x, y)) — произвольная точка эллипса. Расстояние от (M) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+frac{a}{varepsilon}|=frac{1}{varepsilon}(varepsilon x+a).nonumber
$$
Из формулы eqref{ref4} мы видим теперь, что (r_{2}/d_{2}=varepsilon).
Обратно, пусть для какой-то точки плоскости (r_{2}/d_{2}=varepsilon), то есть
$$
sqrt{(x+c)^{2}+y^{2}}=varepsilon left(x+frac{a}{varepsilon}right).nonumber
$$
Так как (varepsilon=c/a), это равенство легко приводится к виду eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_{0}(x_{0}, y_{0})) — точка на эллипсе и (y_{0} neq 0). Через (M_{0}) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_{0} > 0) это график (f_{1}(x)=bsqrt{1-x^{2}/a^{2}}), для (y_{0} < 0) — график (f_{2}(x)=-bsqrt{1-x^{2}/a^{2}}). Не уточняя знака (y_{0}), обозначим подходящую функцию (f(x)).) Для нее выполнено тождество
$$
frac{x^{2}}{a^{2}}+frac{(f(x))^{2}}{b^{2}}=1.nonumber
$$
Дифференцируем его по (x):
$$
frac{2x}{a^{2}}+frac{2ff’}{b^{2}}=0.nonumber
$$
Подставляя (x=x_{0}) и (f(x_{0}=y_{0})), находим производную от (f) в точке (x_{0}), равную угловому коэффициенту касательной:
$$
f'(x_{0})=frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}.nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}(x-x_{0}).nonumber
$$
Упрощая это уравнение, учтем, что (b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}), так как (M_{0}) лежит на эллипсе. Результату можно придать вид
$$
frac{xx_{0}}{a^{2}}+frac{yy_{0}}{b^{2}}=1.label{ref8}
$$
При выводе уравнения eqref{ref8} мы исключили вершины эллипса ((a, 0)) и ((-a, 0)), положив (y_{0} neq 0). Для этих точек оно превращается, соответственно, в уравнения (x=a) и (x=-a). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение eqref{ref8} определяет касательную для любой точки (M_{0}(x_{0}, y_{0})) на эллипсе.
Утверждение 5.
Касательная к эллипсу в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Нам надо сравнить углы (varphi_{1}) и (varphi_{2}), составленные векторами (overrightarrow{F_{1}M_{0}}) и (overrightarrow{F_{2}M_{0}}) с вектором (boldsymbol{n}), перпендикулярным касательной (рис. 8.5). Из уравнения eqref{ref8} находим, что (boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})), и потому
$$
(overrightarrow{F_{1}M_{0}}, boldsymbol{n})=frac{x_{0}}{a^{2}}(x_{0}-c)+frac{y_{0}}{b^{2}}y_{0}=1-frac{x_{0}c}{a^{2}}=frac{a-varepsilon x_{0}}{a}.nonumber
$$
Используя eqref{ref4}, мы получаем отсюда, что (cos varphi_{1}=1/(a|boldsymbol{n}|)). Аналогично находим (cos varphi_{2}=1/(a|boldsymbol{n}|)). Утверждение доказано.