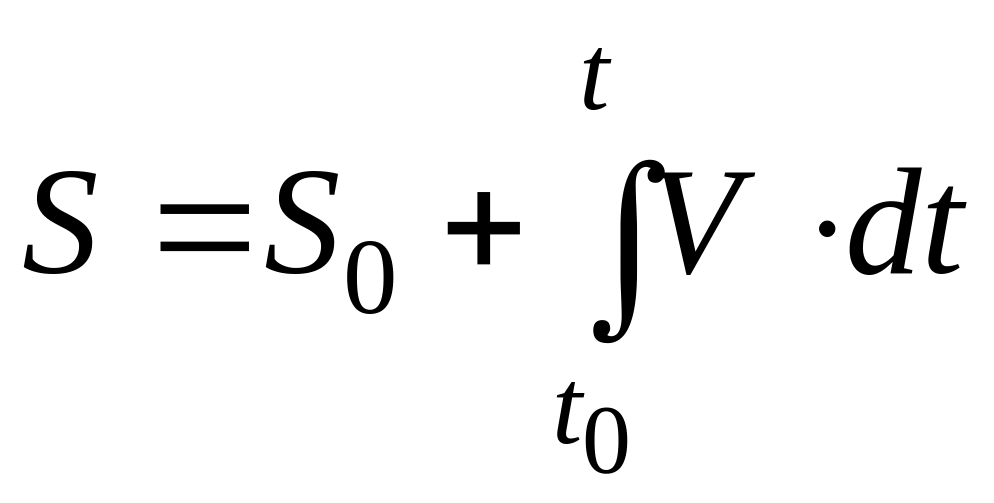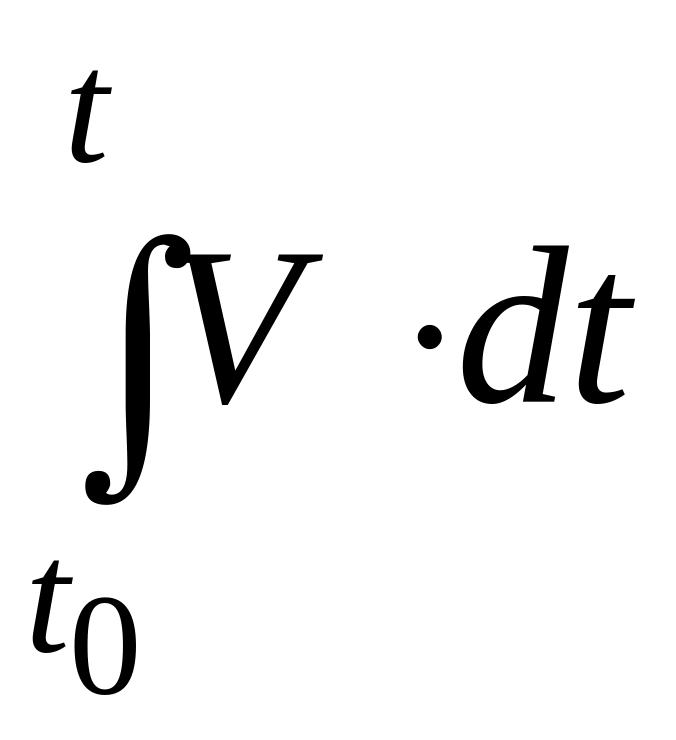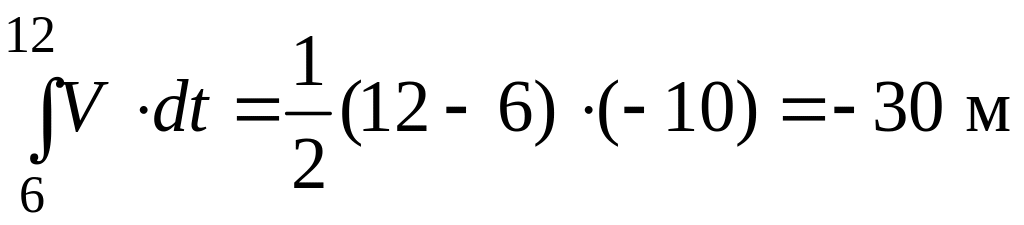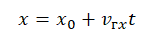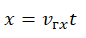Как найти координаты остановок

Подробности

Обновлено 06.03.2019 16:09

Просмотров: 395

1. С какими величинами производят вычисления — с векторными или скалярными?

Вычисления производят не с векторами, а со скалярными величинами, т.е. с проекциями векторов на координатные оси и с модулями векторов или их проекций.

5. Как рассчитать координату движущегося тела, зная координату его начального положения и вектор перемещения?

Спроецировав начала и концы векторов перемещения s₁ и s₂ на ось ОХ, получим отрезки s_1x и s_2x, которые являются проекциями указанных векторов.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси.

Значит, в данном случае:

s_1x > 0,
s_2x < 0.

Из чертежа видно, что координаты х₁ и х₂ можно найти следующим образом:
x₁ = x₀ + s_1x
х₂ = х₀ + s_2x

Расстояние l между двумя телами равно модулю разности их координат:
l = |х₁ — х₂|

По уравнениям можно рассчитать искомые координаты х₁ и х₂.
Но какие числа следует подставить в уравнения вместо символов х₀, s_1x и s_2x?

Согласно условию задачи автобусы встретились на расстоянии 1000 м от остановки, значит, длина отрезка Ох₀ равна 1000 м.
Координата x₀ находится на положительной полуоси ОХ, т. е. х₀ > 0.
Значит, х₀ = 1000 м.

Поскольку ось ОХ параллельна векторам перемещений автобусов, длины проекций s_1x и s_2x равны соответственно длинам векторов s₁ и s₂ (как противоположные стороны построенных на них прямоугольников).
А это означает, что модуль каждой проекции равен модулю соответствующего ей вектора.

Указанные в задаче расстояния (600 м и 500 м), на которые сместились автобусы за время t, представляют собой модули векторов их перемещений.
Значит, модуль проекции s_1x равен 600 м, а модуль проекции s_2x равен 500 м.

Поскольку проекция s_1x положительна, то можно записать:
s_1x = 600 м.
Но проекция s_2x отрицательна, поэтому:
s_2x = -500 м.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

ПОЖАЛУЙСТА , ПОЖАЛУЙСТА , ПОЖАЛУЙСТА ЛЮДИ ПОМОГИТЕ НУЖНО СРОЧНО .
Уравнение движения точки по прямой имеет вид : x = 2t 2 — 4t + 8 (м) .

1 ) Найти перемещение точки за промежуток времени от t1 = 0 c до t 2 = 3 с

2 ) Найти время остановки

3 ) Найти координату остановки

4 ) Найти путь, пройденный точкой за промежуток времени от t1 = 0 c до t 2 = 3 с

5 ) Найти среднюю скорость точки за промежуток времени от t1 = 0 c до t 2 = 3 с

6 ) Найти среднее ускорение точки за промежуток времени от t1 = 0 c до t 2 = 3 с

7 ) Найти скорость тела в момент времени t 2 =2 с

8 ) Найти ускорение точки в момент времени 3 с

Скорость
V
точки и закон ее движения по траектории,
т. е. закон S
= f(t)
изменения
ее дуговых координат с течением времени,
связаны зависимостями

и

,

где S₀
– значение
дуговой координаты точки в начальный
момент времени, S₀
= ОМ₀
= 25 м.

Определенный
интеграл

можно вычислить (в соответствии с его
геометрическим смыслом) с помощью
графика изменения скорости.

Имеем (за промежуток
времени от 0 до 2 с, рис П.6, б):

а за промежуток
времени от 6 до 12 с:

и т. д.

С учетом этого
находим значение дуговых координат в
интересующие моменты времени. Результаты
вычислений заносим в таблицу, а на
рисунке траектории указываем положение
точки в эти моменты (точка М₀,
М₁,
М₂
и т. д.)

В отличие от дуговой
координаты точки путь, пройденный ею
за любой промежуток времени, не может
быть отрицательным и складывается из
модулей приращений дуговых координат
за эти промежутки:

.

Результаты и этих
вычислений заносим в таблицу.

Дуговая координата точки и пройденный путь

Из таблицы и
рисунка, на котором указаны последовательные
положения точки на траектории в различные
моменты времени, следует:

1) точка двигалась
в положительном направлении из положения
М₀
в положение М₃,
пройдя путь 90 м;

2) в момент времени
6 с произошла мгновенная остановка точки
и она начала двигаться в обратном
направлении: дуговая координата начала
уменьшаться, а пройденный путь,
естественно, продолжал увеличиваться;

3) в момент времени
12 с точка попала в положение М₅
на расстоянии 85 м от точки О,
отсчитываемом вдоль траектории. Здесь
произошла ее остановка.

За
весь промежуток времени от t₀
с до t₅
= 12 с точка прошла путь 120 м.

2. Касательное ускорение. Характер движения точки

Из
графика движения точки видно, что
величина скорости точки изменяется.
Изменение величины скорости описывается
ее касательным ускорением

.

Поскольку график
изменения скорости состоит из прямолинейных
кусочков, то

можно
определить на каждом интервале плавного
изменения скорости по формуле:

.

Так, на промежутке
времени от t₀
= 0 с до t₁
= 2 с имеем:

м/с;

с.

Поэтому здесь

м/с².

На промежутке
времени от t₁
= 2 с до t₂
= 5 с:

и, следовательно,

.
А на промежутке от t₂
= 5 с до t₃
= 6 с:

м/с и

с.

Тогда

м/с²
и т. д.

Полностью график
изменения касательного ускорения точки
показан на рис. 6, г. После анализа
вышеуказанного рисунка, а также исходного
графика изменения скорости, можно
сделать следующие выводы:

1. в
   промежуток времени от t₀
   = 0 с до t₁
   = 2 с точка движется ускоренно (знаки

   и

   – одинаковые). Причем
   

   и, следовательно, движение происходит
   в положительном направлении (в сторону
   возрастания дуговой координаты).
   Наконец, т. к.
   
   ,
   то движение точки равноускоренное;

2. на промежутке
   времени от t₁
   = 2 с до t₂
   = 5 с V
   = const
   (равномерное движение). Так как

   ,
   то движение точки происходит в
   положительном направлении;

3. от t₂
   = 5 с до t₃
   = 6 с точка движется равнозамедленно,
   но все еще в положительном направлении;

4. на промежутке
   времени от t₃
   = 6 с до t₄
   = 10 с точка движется равноускоренно
   назад (

   и
   
   ;

   ).

5. на последнем
   промежутке времени от t₄
   = 10 с до t₅
   = 12 с точка движется равнозамедленно,
   в отрицательном направлении (

   и
   
   ;

   )

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  31.05.20155.97 Mб12Сборник задач по физике — Чертов- Воробьёв.doc

• #
• #
• #
• #
• #
• #

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 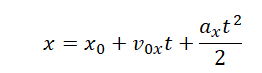Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Механическое движение

О чем эта статья:

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

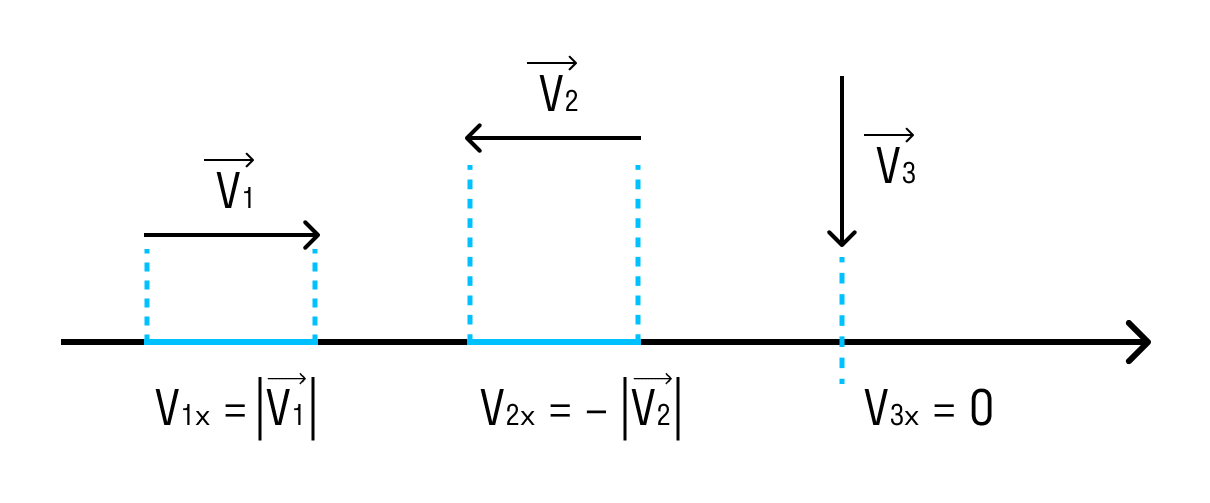
Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Формула координаты тела при равномерном прямолинейном движении

Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.

Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:

Формула координаты тела при прямолинейном равномерном движении

x₀ — координата тела в начальный момент времени,

x — координата тела в текущий момент времени,

t — время движения,

V — скорость тела

Таким образом, необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат: