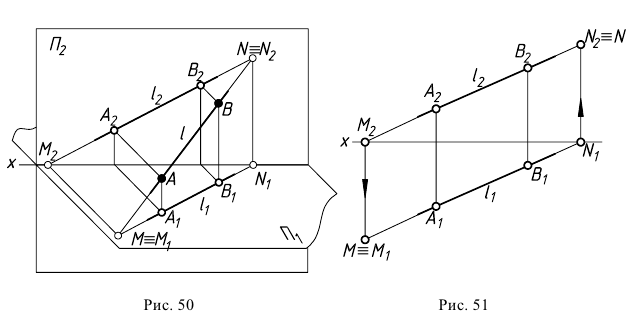
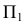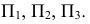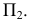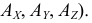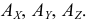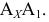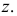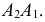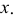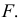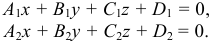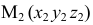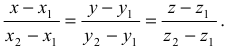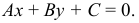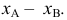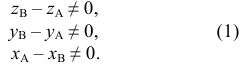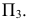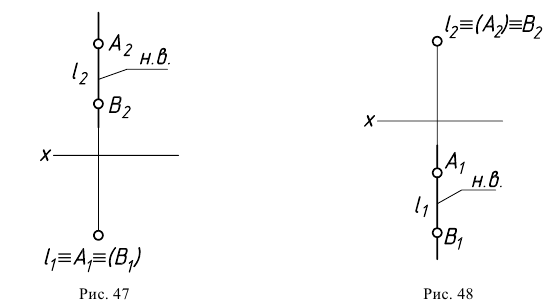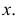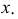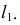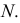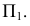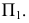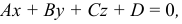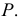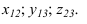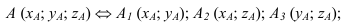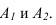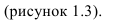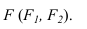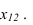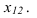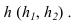Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
- Записать их координаты.
- Достроить проекции т. A и B на плоскость П3.
- Определить положение точек в пространстве (октант или плоскость проекций).
- Построить наглядное изображение точек в системе плоскостей П1, П2, П3.
Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B – т. В’. Так как она лежит на оси х, то Bx = B’ и координата Bу = 0. Абсцисса x точки B равна длине отрезка BхO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B» к оси z, таким образом найдем Bz. Аппликата z точки B равна длине отрезка BzO со знаком минус, так как Bz лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П2. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки Aх и Aу. Пересечение перпендикуляров, восстановленных из Aх и Aу соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.
Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П2 по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из Bх и Bz, определит положение точки B.
Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
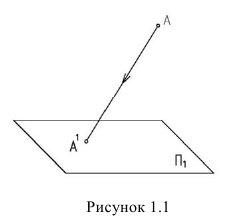
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1.Найти проекцию M1 точки M0(4, -3, 2) на плоскость
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=−8.
Координаты точки M0: x0=4, y0=−3, z0=2.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (7) находим:
Ответ:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Содержание:
Ортогональное проецирование:
Из всех методов проецирования ортогональное нашло наиболее широкое применение в инженерной практике в силу ряда своих преимуществ.
Метод Монжа. Октанты пространства
Наиболее важным из них является возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. При этом при получении ортогонального чертежа, обладающего полной обратимостью, необходимо иметь, как было отмечено ранее, по крайней мере, две связанные между собой ортогональные проекции оригинала. Наиболее удобной для фиксирования положения геометрического образа в пространстве и выявления его формы по ортогональным проекциям является система из трех взаимно перпендикулярных плоскостей проекций. Такой плоскостной макет представлен на рис. 29. При этом различают:
Плоскости проекций пересекаются по трем взаимно перпендикулярным прямым, которые называются осями проекций 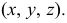
В большинстве европейских стран принята система расположения плоскостей проекций, при которой положительными направлениями осей считают: для оси 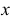
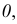
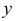
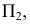
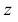
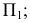
Плоскости проекций делят пространство на восемь частей — октантов. Октанты условно принято нумеровать, как показано на рис. 29.
Принято, что наблюдатель всегда находится в первом октанте. Плоскости проекций считаются непрозрачными, поэтому видимы только точки (геометрические фигуры), расположенные в I октанте, а также на полуплоскостях
Пользоваться пространственным макетом для изображения проекций оригинала неудобно ввиду его громоздкости. Поэтому его реконструируют в эпюр Монжа — чертеж, составленный из двух или трех связанных между собой ортогональных проекций геометрической фигуры.
Преобразование пространственного макета в эпюр осуществляется путем совмещения плоскостей 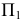
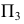
Для совмещения плоскости 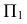
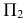
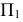
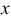
Для совмещения 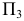
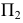
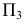
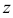
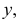
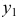
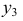
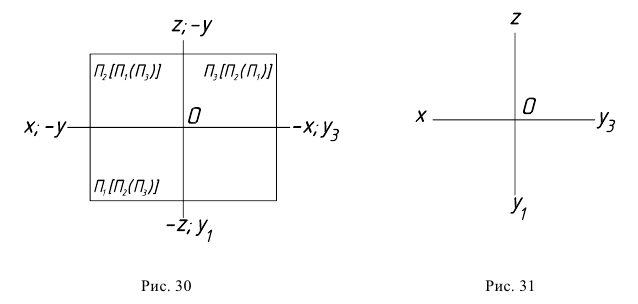
После совмещения плоскостей проекций пространственный макет примет вид, показанный на рис. 30.
Обычно не указывают обозначение полуплоскостей проекций и отрицательное направление осей. Тогда, в окончательном варианте, эпюр принимает вид, показанный на рис. 31.
Проекции точки
Точка — одно из основных базовых понятий геометрии. Для отображения этого простейшего геометрического образа на плоскости целесообразно понимать под точкой физический объект, имеющий линейные размеры. При этом условно за точку принимают шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.
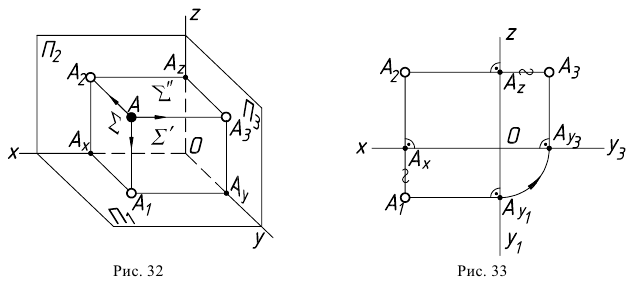
Для построения эпюра точки следует руководствоваться первым инвариантным свойством ортогонального проецирования: «Проекция точки есть точка». Пусть даны в пространстве точка 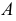
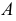
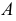
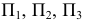
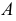
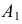
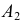
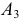
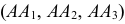
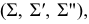
Для получения эпюра точки 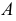
На эпюре (рис. 33) проекции точки будут располагаться на прямых, перпендикулярных к осям проекций и проходящих через точки
Эти прямые, являющиеся проекциями соответствующих проецирующих лучей, называют линиями проекционной связи.
Горизонтальная 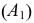
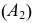
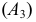
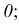
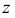
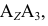
Прямоугольные координаты точки
Система трех взаимно перпендикулярных плоскостей проекций аналогична декартовой системе координатных плоскостей. При этом оси проекций соответствуют осям координат с началом в точке 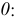
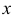
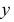
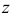
Исходя из этого, положение точки в пространстве может быть определено тремя координатами: 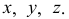
Анализируя эпюр (рис.34), можно отметить, что каждая из проекций точки 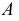
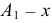
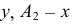
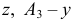
Из этого следует, что положение точки в пространстве вполне определяется положением ее двух ортогональных проекций.
Точка в октантах пространства
На рис. 29 было показано, что плоскости координат в своем пересечении образуют восемь трехгранных углов — восемь октантов.
Зная положительное и отрицательное направление осей, по координатам точки можно также определить, в каком октанте расположена точка:
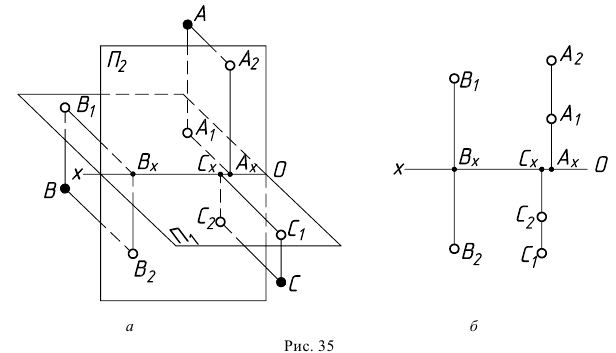
На рис. 35,а показаны точки 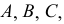
Безосный чертеж
Большинство задач начертательной геометрии решают, не устанавливая метрической связи с плоскостями проекций. Вследствие этого построения на чертеже можно выполнять в безосной системе плоскостей проекций, т.е. без указания положения осей (рис. 36).
Имея такой чертеж, можно, при необходимости, всегда ввести оси и тем самым задать расстояние от точки до условно выбранных плоскостей 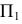
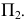
Перенесение оси на чертеже вверх или вниз соответствует параллельному переносу в пространстве двугранного угла 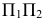
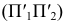
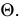
На эпюре такому параллельному переносу двугранного угла соответствует перемещение начала координат — точки 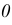
Рис. 39 демонстрирует построение на безосном чертеже профильной проекции точки 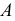
Построение выполнено с помощью постоянной чертежа 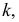
Конкурирующие точки
Геометрические образы могут быть взаимно расположены таким образом, что некоторые из них (или отдельные их части) будут закрыты от наблюдателя.
Построение границы видимости образов на чертеже выполняется на основании выявления и анализа конкурирующих точек.
Конкурирующими называют точки, лежащие на одном проецирующем луче.
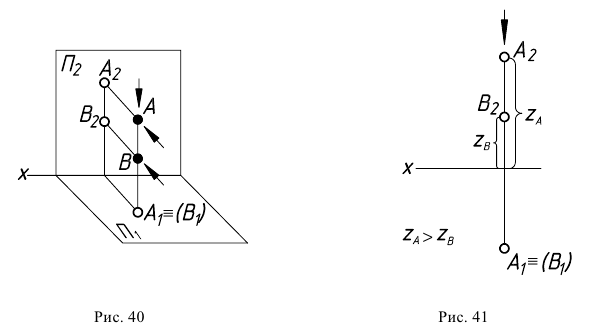
Для определения видимости конкурирующих точек рассуждают следующим образом (рис. 40). Точки 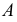
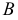
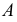
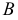
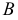
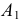
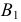
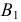
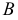
На 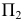
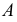
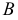
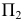
На эпюре (рис. 41) вопрос видимости точек 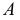
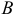
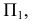
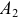
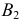
Фронтальная проекция точки 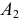
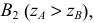
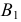
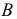
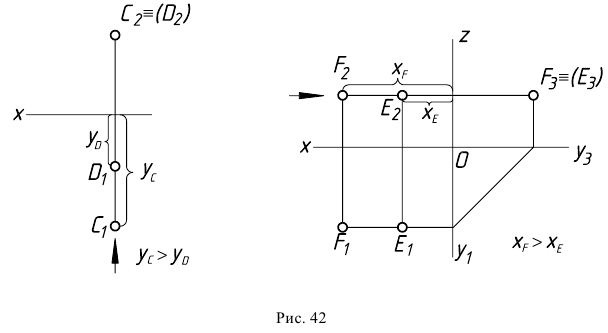
Аналогично рассуждают, определяя видимость конкурирующих точек и относительно других плоскостей проекций (рис. 42).
На рис. 42 показаны фронтально-конкурирующие точки 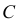
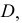
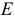
Проекции прямых линий
Наряду с точкой прямая линия является одним из исходных понятий в геометрии. Прямая является простейшей из линий (более подробно линии будут рассмотрены в разделе V), которой в начертательной геометрии отводится важная роль при решении инженерных задач.
Аналитически прямую в пространстве можно задать разными способами. Например, как уравнение прямой, полученной при пересечении двух плоскостей:
Другим, более удобным, является уравнение прямой, проходящей через две заданные точки 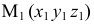
Если рассматривать прямую на плоскости, то общим уравнением ее будет
При построении эпюра прямой следует использовать третье свойство проецирования: «Проекция прямой есть прямая». Другими словами, для определения проекции прямой достаточно задать проекции двух не тождественных точек, принадлежащих этой прямой.
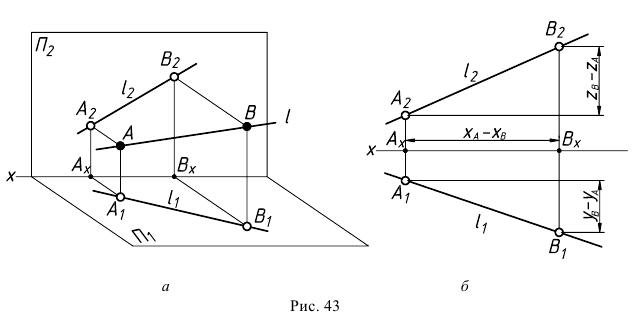
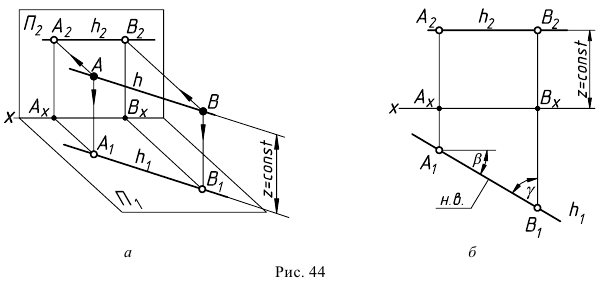
Пусть прямая 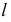
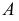
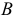
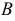
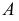
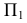
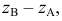
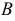
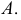
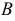
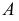
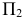
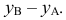
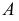
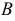
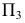
Прямая линия общего положения
Такая прямая занимает в системе плоскостей проекций произвольное положение (углы наклона прямой к плоскостям 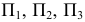
На эпюре прямой общего положения (см. рис. 43, б) нет натуральной величины отрезка и углов его наклона к плоскостям проекций.
Частные случаи расположения прямой
Прямая линия, кроме произвольного, может занимать следующие положения относительно плоскостей проекций:
- — параллельное одной из плоскостей проекций (прямые уровня);
- — перпендикулярное какой-нибудь плоскости проекций (проецирующие прямые).
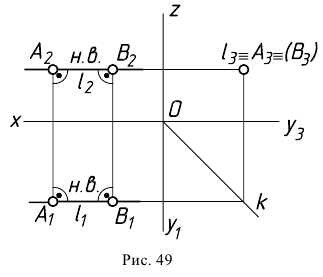
Прямые уровня
Прямые линии, параллельные (но не перпендикулярные) плоскостям проекций, называют линиями уровня. Таких линий три:
Если в условии (1) будем иметь: 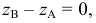
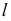
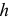
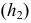
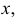
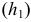
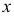
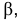
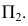
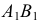
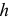
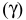
Если в условии (1) 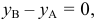
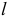
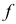
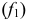
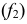
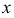
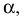
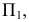
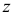
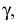
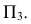
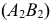
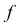
Аналогично, если в условии (1) 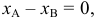
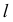
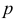
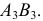
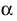
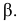
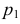
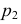
Проецирующие прямые
Прямые линии, перпендикулярные плоскостям проекций, называют проецирующими. Различают следующие проецирующие прямые:
Проецирующие прямые в то же время параллельны двум координатным плоскостям проекций.
Если в условии (1) для прямой общего положения 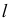
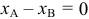
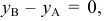
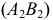
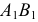
Если в условии (1) примем 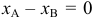
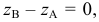
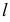
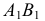
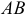
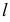
И, наконец, если в условии (1) 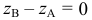
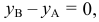
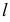
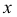
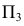
Понятие о следах прямой
Точки пересечения прямой линии с координатными плоскостями проекций называют следами прямой. Соответственно точку пересечения прямой с горизонтальной плоскостью проекций 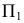
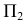
На рис. 50 прямая 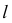
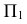
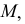
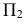
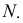
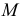
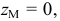
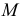
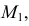
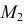
Точка 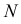
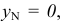
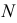
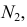
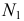
Построение следов на эпюре показано на рис. 51.
Чтобы найти горизонтальный след 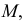
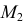
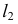
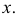
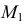
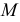
Чтобы найти фронтальный след 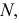
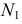
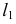
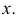
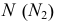
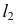
Если прямая параллельна плоскости проекций, то следом ее на этой плоскости является несобственная точка.
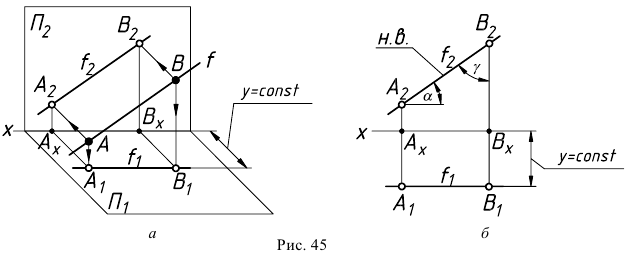
Натуральная длина отрезка прямой и углы его наклона к плоскостям проекций
На эпюре натуральная длина отрезка прямой и углы его наклона видны только в случае его частного расположения относительно плоскостей проекций.
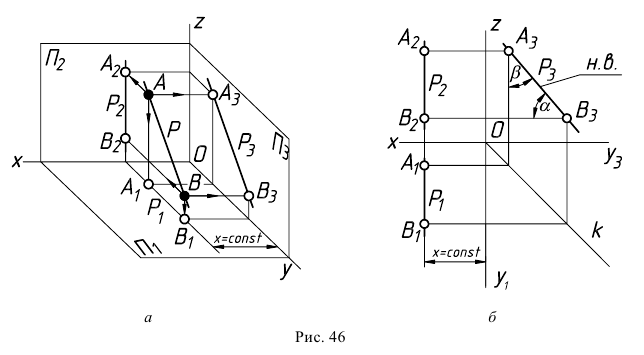
Если же прямая занимает общее положение относительно плоскостей проекций, то для нахождения натуральной величины отрезка этой прямой и углов его наклона к плоскостям проекций можно использовать соответствующее свойство ортогонального проецирования (свойство 12).
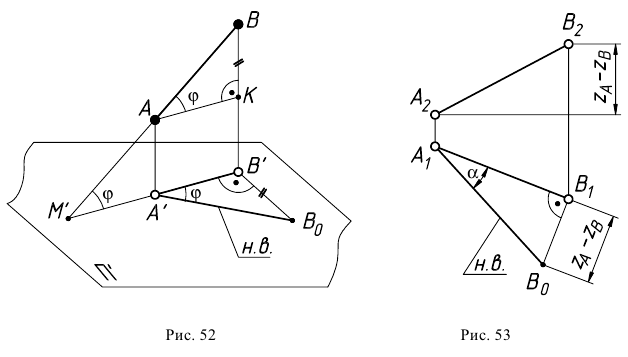
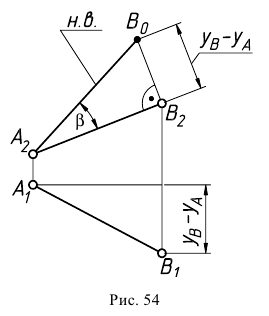
Используя это свойство, на плоскости проекций 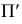
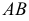
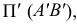
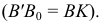
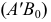
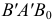
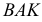
Аналогичные построения можно выполнить на эпюре прямой (рис.53).
Принимаем плоскость 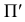
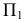
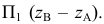
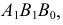
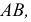
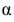
Аналогичные построения можно выполнить, принимая плоскость 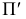
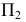
Такой прием нахождения натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций называют способом прямоугольного треугольника.
Взаимное расположение двух прямых
Две прямые в пространстве могут пересекаться, быть параллельны друг другу или скрещиваться.
Пересекающиеся прямые. Прямые линии, имеющие общую точку, называются пересекающимися.
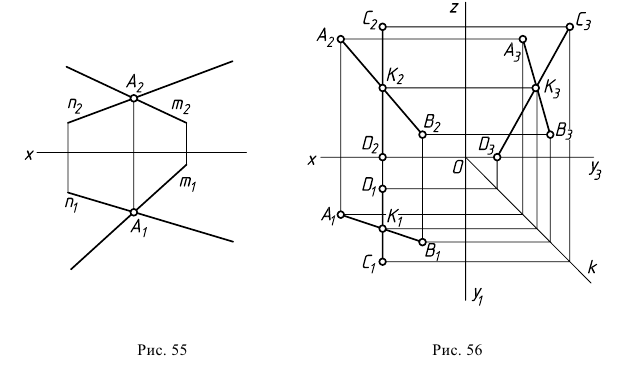
Если прямые пересекаются в пространстве, то их одноименные проекции также пересекаются, и проекции точки пересечения лежат на одной линии связи. Для подтверждения пересечения прямых на чертеже бывает достаточно двух проекций (рис. 55). Однако, если хотя бы одна из прямых является линией уровня, то одной из двух проекций должна быть проекция на ту плоскость, которой параллельна эта линия уровня (рис. 56).
Параллельные прямые. Прямые линии, пересекающиеся в несобственной точке, называются параллельными.
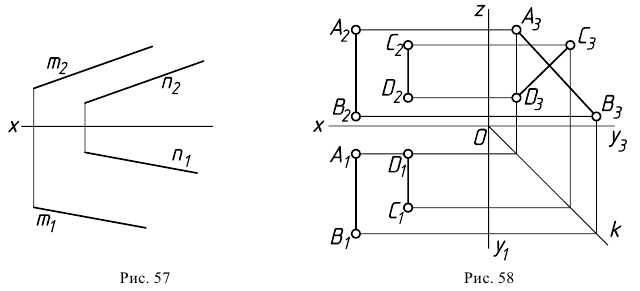
Если две прямые параллельны в пространстве, то их одноименные проекции тоже параллельны. Для подтверждения параллельности прямых 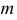
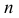
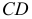
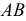
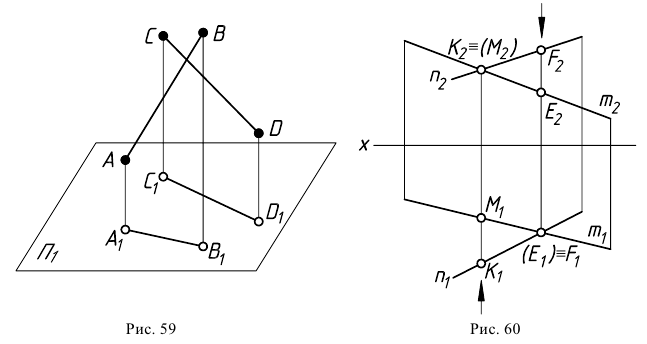
Скрещивающиеся прямые. Прямые, не пересекающиеся и не параллельные между собой, называются скрещивающимися. На рис. 59 показана пространственная модель таких прямых.
Если прямые скрещиваются в пространстве, то на эпюре их одноименные проекции могут пересекаться, но точки их пересечения не лежат на одной линии связи (не являются проекциями одной точки) (рис. 60). Так, точка пересечения фронтальных проекций скрещивающихся прямых 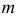
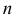
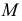
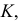
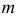
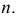
Аналогично, точка пересечения горизонтальных проекций 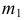
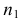
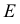
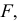
Точки пересечения одноименных проекций скрещивающихся прямых являются конкурирующими. Их видимость на эпюре определяют, как и видимость любых конкурирующих точек, по величине удаления от плоскости, на которой их проекции совпадают. Невидимые точки условно заключают в скобки.
Проекции плоскости
Наряду с точкой и прямой, плоскость также относится к основным базовым понятиям в начертательной геометрии.
Плоскость является простейшей поверхностью. Между декартовыми координатами принадлежащих ей точек существует зависимость, аналитически выраженная в форме многочлена первой степени:
т.е. плоскость — поверхность первого порядка.
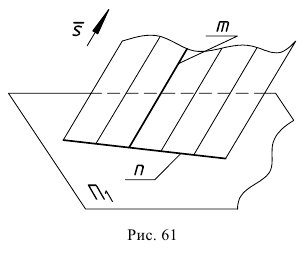
Кинематическое образование плоскости, как простейшей поверхности, может быть представлено (рис. 61) перемещением прямой 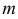
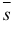
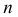
Положение плоскости в пространстве однозначно определяется тремя различными точками 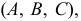
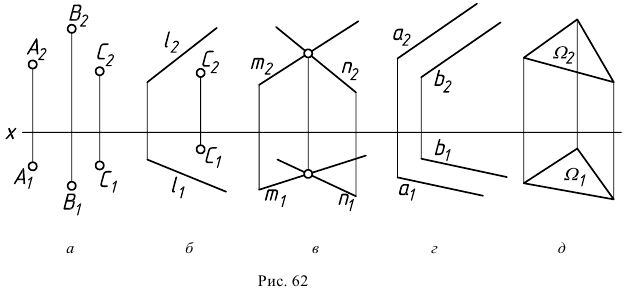
- — трех различных точек, не принадлежащих одной прямой (рис.62,а);
- — прямой и точки вне ее (рис. 62, б);
- — двух прямых, пересекающихся в собственной (рис. 62, в) или в несобственной (рис. 62, г) точке;
- — отсека плоской фигуры (рис. 62, д).
В некоторых случаях бывает целесообразным задавать плоскость прямыми, по которым эта плоскость пересекает плоскости проекций. Такой вариант задания плоскости называют заданием плоскости следами.
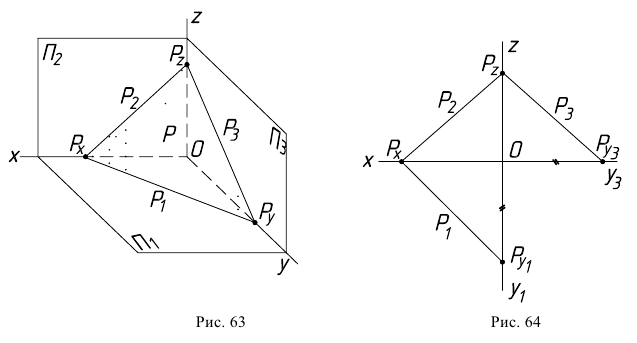
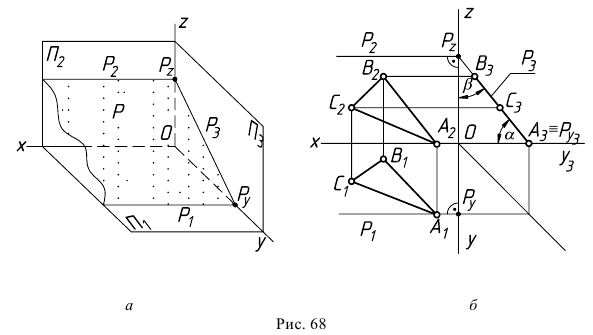
На рис. 63 показаны плоскость 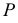
Точки 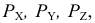
Всегда можно перейти от одного вида задания плоскости к любому другому. Например, на рис. 65 показано, как от задания плоскости двумя пересекающимися прямыми 
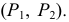
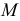
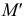
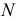
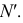
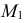
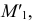
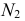
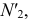
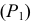
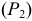
Плоскость общего положения
На приведенных выше примерах заданная плоскость занимает произвольное положение по отношению к плоскостям проекций (углы наклона этой плоскости к плоскостям проекций отличны от 0° к 90°). Такая плоскость называется плоскостью общего положения.
На эпюре такой плоскости не сохраняются метрические характеристики плоской фигуры и не видны углы наклона ее к плоскостям проекций.
Частные случаи расположения плоскости
Кроме рассмотренного общего случая плоскость по отношению к плоскостям проекций может занимать следующие положения:
- — перпендикулярное одной из плоскостей проекций (проецирующие плоскости);
- — параллельное одной плоскости проекций (плоскости уровня).
Проецирующие плоскости
Плоскости, перпендикулярные одной из плоскостей проекций, называют проецирующими. При этом различают три типа проецирующих плоскостей:
Характерной особенностью проецирующих плоскостей является то, что сами плоскости и любые геометрические фигуры, лежащие в них, проецируются на плоскости проекций, им перпендикулярные, в виде прямых линий. Такое свойство проекций проецирующих плоскостей называется собирательным.
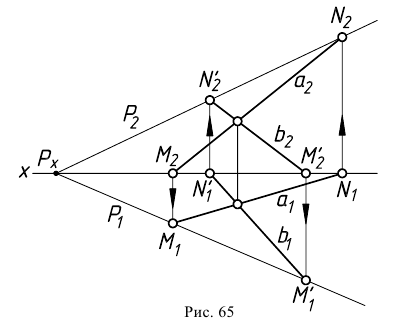
Например, на рис. 66, 6 горизонтально-проецирующая плоскость, заданная двумя следами — горизонтальным 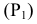
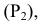
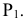
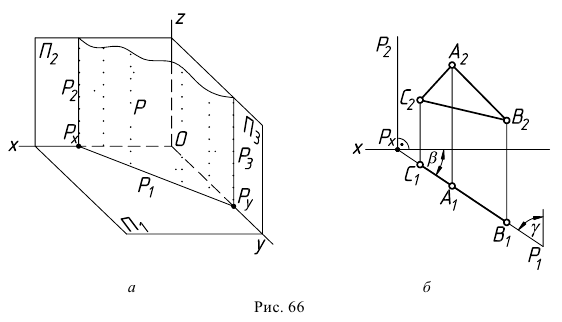
Проецирующие плоскости на эпюре удобнее задавать следами. При этом след (проекция), обладающий собирательным свойством, несет информацию об углах наклона проецирующей плоскости к неперпендикулярным ей плоскостям проекций (рис. 66, б — 68, б). Два других ее следа перпендикулярны той же плоскости проекций, какой перпендикулярна сама плоскость. Эти два следа не играют важной роли в определении плоскости, поэтому на безосном чертеже проецирующие плоскости обычно задают одним следом — линией пересечения только с той плоскостью, которой они перпендикулярны.
Плоскости уровня
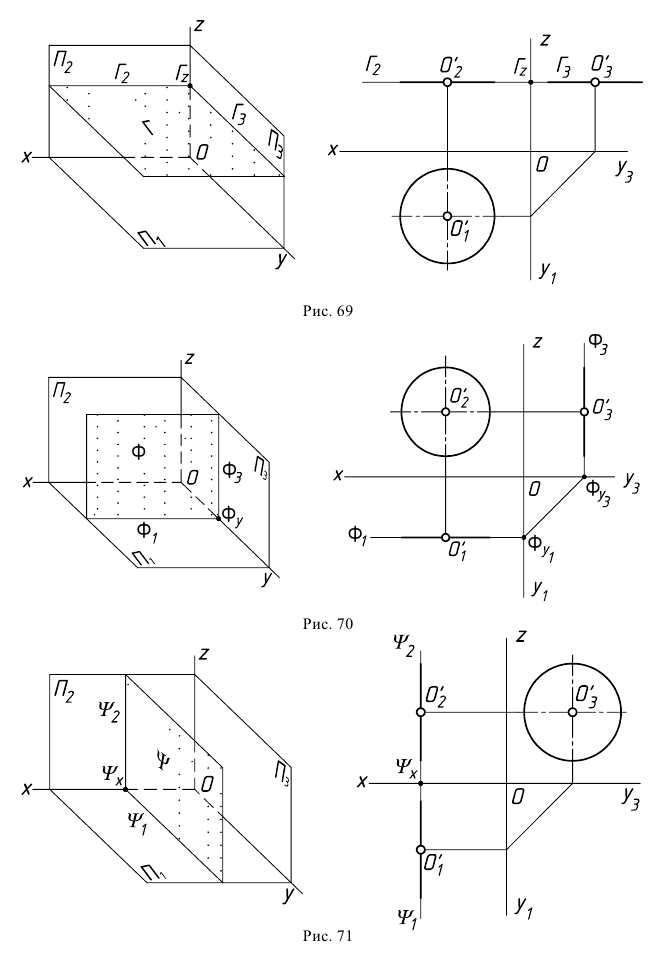
Плоскости, параллельные какой-либо плоскости проекций, называют плоскостями уровня. Различают три типа таких плоскостей:
Характерной особенностью таких плоскостей является то, что плоские фигуры, расположенные в них, проецируются без искажения на ту плоскость проекций, которой плоскости уровня параллельны. Две другие проекции (следы) плоскости уровня — прямые, параллельные соответствующим осям проекций. На безосном чертеже обычно задают плоскости уровня одним (любым) следом.
Изображение точки, примой, плоскости и простейших геометрических поверхностей в ортогональных проекциях
Предмет, задачи и метод начертательной геометрии:
Начертательная геометрия это наука изучающая методы изображения реальных пространственных объектив — зданий, сооружений, деталей машин — состоящих из совокупности точек, линий, поверхностей и методы решения геометрических задач но данным изображениям. Вместе с этим решается и очень существенная задача — развитие пространственного воображения.
Метод начертательной геометрии — метод проекций. Так как любой предмет можно рассматривать как совокупность множества точек, то сущность метода проецирования рассмотрим на примере точки.
- Заказать чертежи
Прямоугольные проекции и координаты точек. Эпюр (чертеж) Г.Монжа. Изображение проекций точек при различном их положении в пространстве
Для построения проекции точки, зададим плоскость 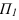
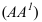
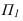
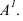
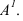
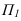
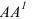
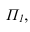
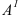
ортогональной проекцией точки А.
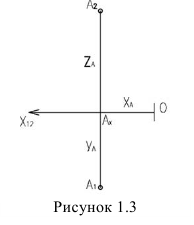
На рисунке 1.1 видно, что одна проекция точки не определяет ее положения в пространстве, так как в точку 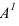
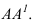
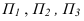
Плоскости проекций пересекаясь дают оси проекций —
Спроецируем ортогонально точку А на эти плоскости проекций. Получим соответственно:
В трехмерном пространстве положение точки определяется тремя (декартовыми) координатами А 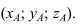
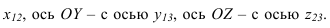
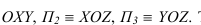
По чертежу видно, что две проекции точки полностью определяют положение точки в пространстве, так как содержат все три координаты.
Для перехода от пространственного чертежа к плоскому, плоскость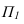
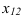
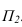
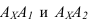
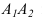
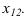
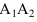
Плоский чертеж состоящий из горизонтальной 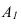
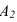
связи 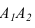
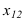
Иногда возникает необходимость по двум проекциям построить третью. На рисунке 1.4 показано построение профильной проекции 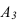
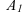
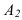
Плоскости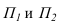
Точки могут находиться в любой четверти, лежать на плоскостях проекций или на осях. Необходимо освоить две задачи.
Первая — по паре проекций точек находящихся на плоскостях проекций определить положение точки в пространстве.
Вторая — но положению точки в пространстве изобразить ее парой проекций.
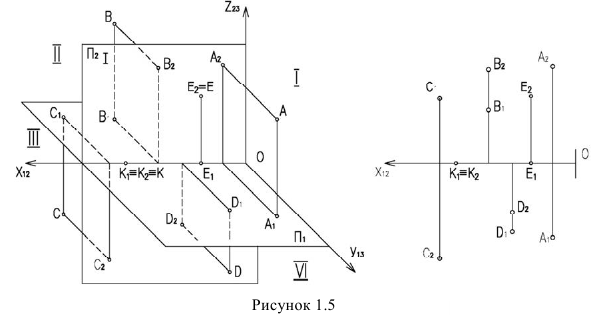
На рисунке 1.5 точка А находится в I четверти. Все ее координаты имеют положительное значение — фронтальная проекция находится над осью 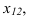
Точка В, находится во II четверти. Ее координата 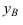
У точки С, находящейся в III четверти отрицательными будут координаты
Фронтальная проекция находится под осью 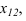
У точки D, находящейся в IV четверти, отрицательная координата 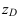
У точки E, находящейся на плоскости 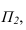
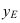
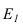
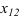
Точка К лежит на оси 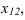
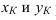
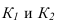
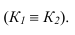
Изображение примой линии в ортогональных проекциях. Прямые общего и частного положении. Следы примой. Взаимное положение точки и примой
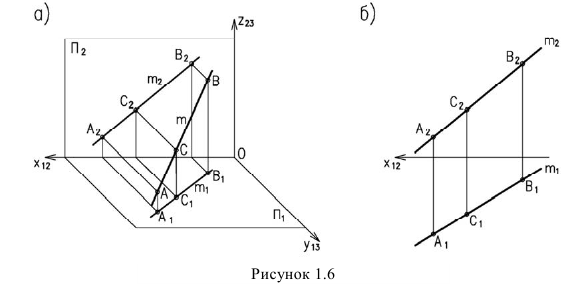
Положение прямой линии в пространстве определяется двумя ее точками. А из свойств параллельного проецирования известно, что проекции прямых являются прямыми линиями. Поэтому, для построения прямой (m) достаточно построить проекции двух её точек (А и В) и одноименные проекции точек соединить прямыми (рисунок 1.6). Отсюда можно сделать вывод если точка лежит на примой, то ее проекции лежат на соответствующих проекциях примой. Если эта точка делит отрезок АВ в каком либо отношении, то в том же отношении проекции точки делят проекции отрезка.
Прямая, не параллельная ни одной из плоскостей проекций, называется примой общего положении. На чертеже ни одна из проекций такой прямой не параллельна оси (рисунок 1.6). Длина ортогональной проекции отрезка прямой общего положения всегда меньше длины самого отрезка.
Прямые частного положения
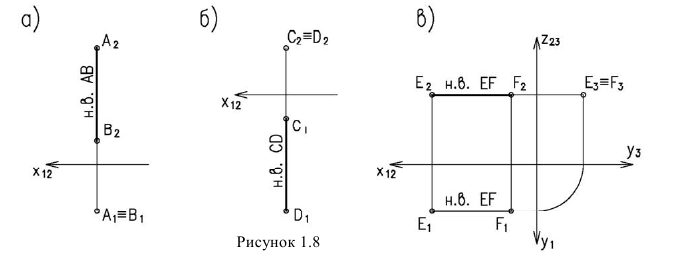
Прямые параллельные или перпендикулярные плоскостям проекций называются прямыми частного положения
Различают два вида прямых частного положения:
- -прямые уровня — прямые параллельные плоскостям проекций; проецирующие -прямые — прямые перпендикулярные плоскостям проекций.
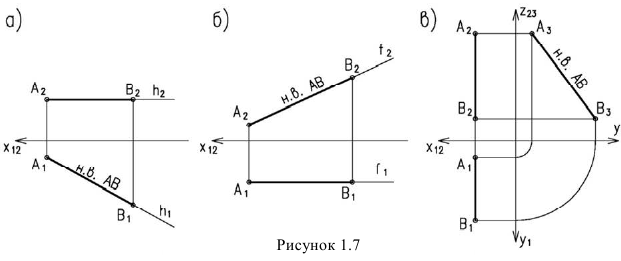
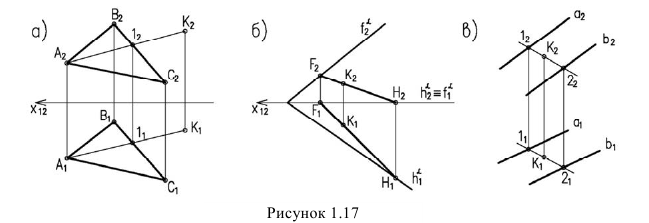
Прямые уровня (рисунок 1.7).
На плоскость проекций, которой прямая уровня параллельна, она проецируется в натуральную величину.
Следы примой
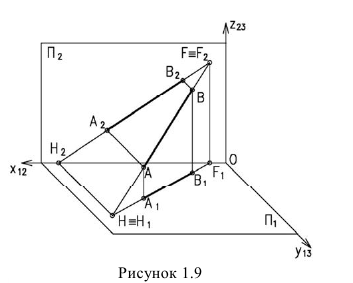
Следами прямой АВ называются точки пересечения ее с плоскостями проекций (рисунок 1.9). Точка H — горизонтальный след прямой АВ. Точка F — фронтальный след прямой АВ.
Так как следы прямой это точки лежащие на плоскостях проекций, то одна из проекций следа находится на оси 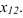
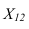
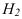
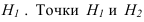
Взаимное положение прямых. Понятие конкурирующих точек
Две прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Их положение в пространстве устанавливается взаимным расположением одноименных проекций.
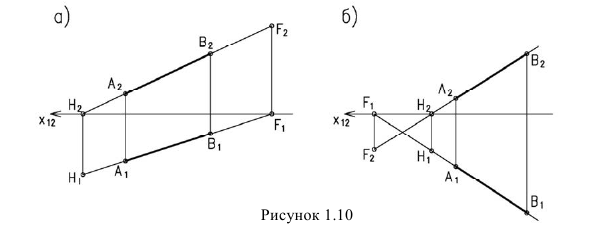
Если в пространстве две прямые параллельны, то их одноименные проекции также параллельны (рисунок 1.11а).
Параллельность профильных прямых не всегда очевидна. Хотя их горизонтальные и фронтальные проекции параллельны, сами прямые могут быть не параллельны. Для определения их взаимного положения можно построить профильную проекцию, (рисунок 1.116).
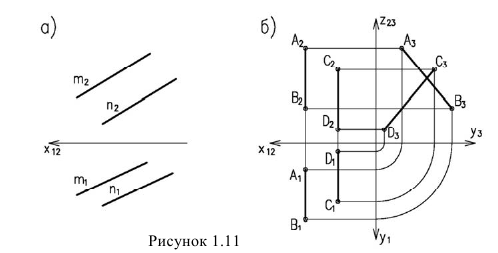
Перeсекающиеси прямые — это прямые, имеющие общую точку, следовательно, если прямые в пространстве пересекаются, то точки пересечения их одноименных проекций лежат на одной линии проекционной связи (рисунок 1.12).
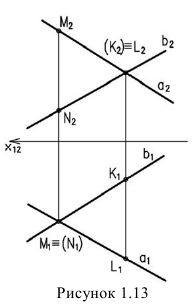
Скрещивающиеся прямые не имеют общей точки, поэтому точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рисунок 1.13).
Пары точек, у которых какие-либо одноименные проекции совпали, т.е. они лежат на одном проецирующем луче, называются конкурирующими (одна из них «закрывает» другую). Точки М и N — горизонтально-конкурирующие, точки К и L — фронтально-конкурирующие. Из двух конкурирующих точек видна та, у которой больше одна из координат (две другие совпадают).
Например, координата Z у точки М больше, чем у точки N , следовательно, прямая а в этом месте расположена выше прямой в и будет видима при взгляде сверху, т.е. на горизонтальной проекции. Аналогично, у точки L координата Y больше, чем у точки K, следовательно, в этом месте прямая а расположена ближе к зрителю и будет видима на фронтальной проекции. Определение видимости конкурирующих точек позволит нам в дальнейшем определять видимость прямой относительно плоскости.
Задание плоскости в ортогональных проекциях. Следы плоскости
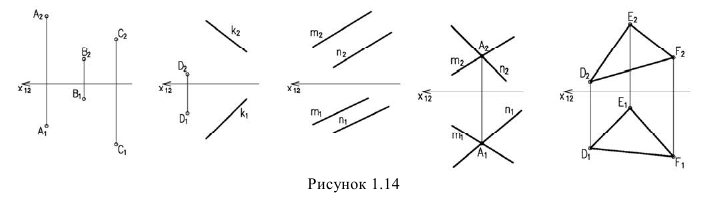
Положение плоскости в пространстве определяется тремя не лежащими на одной прямой точками, прямой и не лежащей на ней точкой, двумя параллельными или пересекающимися прямыми, плоской фигурой. Примеры задания плоскости даны на рисунке 1.14.
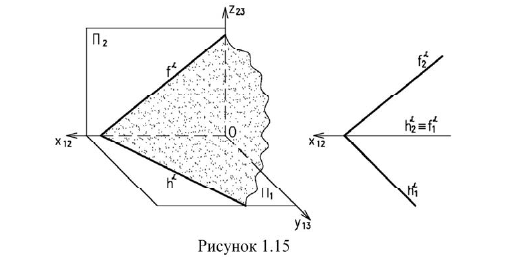
Все изображенные на рисунке 1.14 плоскости являются плоскостями общего положения. Плоскостью общего положения называется плоскость не перпендикулярная ни одной из плоскостей проекций. Плоскость также можно задать следами. Следами плоскости называются линии пересечения плоскости с плоскостями проекций (рисунок 1.15).
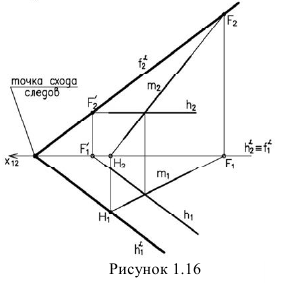
Т.к следы плоскости — прямые линии, то для их построения достаточно найти две точки принадлежащие им. Пели прямые лежат в плоскости, то их следы лежат на следах плоскости. Следовательно для построения следов плоскости достаточно построить следы двух прямых лежащих в этой плоскости (рисунок 1.15).
Фронтальным следом плоскости 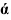
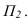
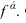
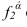
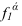
Горизонтальный след плоскости — линия пересечения с горизонтальной плоскостью проекций 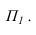
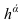
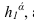
Они имеют общую точку на оси х — точку схода следов.
Прямые и точки в плоскости
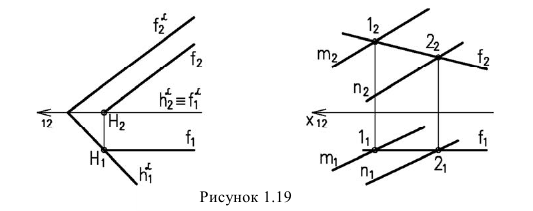
Точка лежит в плоскости, если она лежит на прямой принадлежащей этой плоскости.
Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
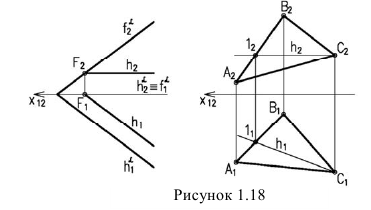
На рисунке 1.17а. фронтальная проекция точки К выбрана произвольно в плоскости а 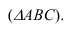
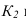
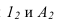
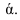
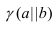
Главные линии плоскости
Главными линиями плоскости называются ее горизонтали, фронтали и линии наибольшего ската.
Горизонтали плоскости — это прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций —
Все горизонтали плоскости параллельны между собой и параллельны горизонтальному следу плоскости. Фронтальные проекции горизонталей параллельны оси 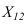
Фронтали плоскости — это прямые, принадлежащие плоскости и параллельны фронтальной плоскости проекций —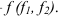
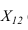
Плоскости частного положения
Плоскости как и прямые относительно плоскостей проекций могут занимать частное положение. Плоскости, перпендикулярные или параллельные одной из плоскостей проекций, называются плоскостями частного положения.
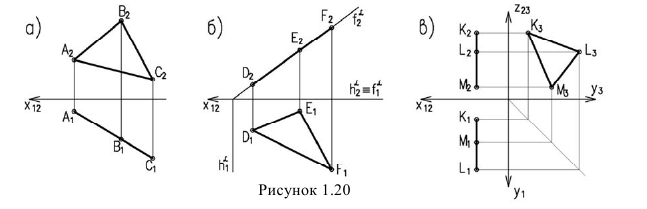
Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими (рисунок 1.20).
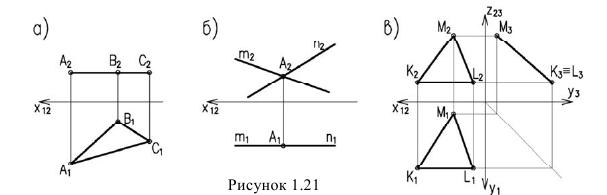
Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня (рисунок 1.21).
Изображение простейших геометрических поверхностей
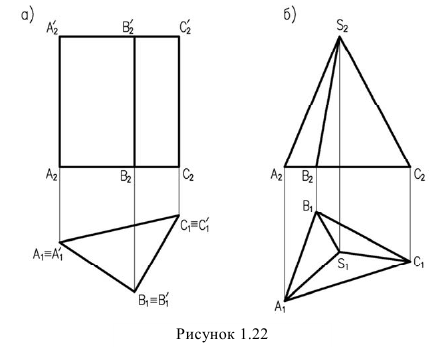
Многогранники представляют собой совокупность отрезков прямых и плоских фигур. На рисунке 1.22 изображены:
- а) трехгранная прямая призма.
- б) трехгранная пирамида.
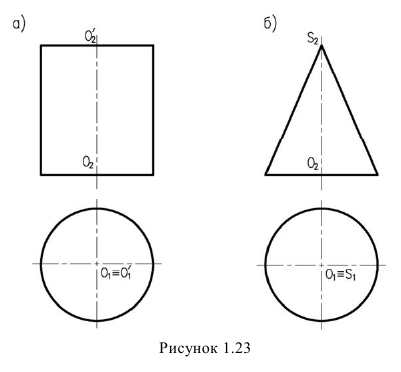
На рисунке 1.23 изображены простейшие кривые поверхности:
- а) прямой круговой цилиндр.
- б) прямой круговой конус.
- Взаимное расположение геометрических образов и фигур
- Преобразование чертежа
- Кривые линии
- Образование и задание поверхности на чертеже
- Пересечение прямой с плоскостью
- Пересечение прямой с поверхностью
- Пересечение поверхностей
- Способы преобразования чертежа
1.1. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Известны два метода проецирования: центральное и параллельное.
Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).
Рисунок 1.1 – Центральное проецирование
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA, SB – проецирующие прямые (проецирующие лучи).
Примечание: левой клавишей мыши можно переместить КРАСНУЮ точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.
Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.
Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Докажем это утверждение.
На рисунке 1.1: точка А1 – центральная проекция точки А на плоскости проекций π1. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С1) на плоскости проекций π1 совпадает с проекцией точки А (А1):
- С ∈ SA;
- SC ∩ π1=C1 → C1 ≡ A1.
Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π2) и ещё один центр проецирования (S2) (Рисунок 1.2).
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств
Построим проекции точки А на плоскости проекций π2. Из всех точек пространства только точка А имеет своими проекциями А1 на плоскость π1 и А2 на π2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).
Свойство 2. Проекция прямой есть прямая.
Докажем данное свойство.
Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π1=А1В1, где А1В1 – центральная проекция прямой, заданной отрезком АВ.
Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.
1.2. Параллельное проецирование
Рассмотрим метод параллельного проецирования. Наложим три ограничения, которые позволят нам, пусть и в ущерб наглядности изображения, получить чертёж более удобным для использования его на практике:
- Удалим оба центра проекции в бесконечность. Таким образом, добьемся того, что проецирующие лучи из каждого центра станут параллельными, а, следовательно, соотношение истинной длины любого отрезка прямой и длины его проекции будут зависеть только от угла наклона этого отрезка к плоскостям проекций и не зависят от положения центра проекций;
- Зафиксируем направление проецирования относительно плоскостей проекций;
- Расположим плоскости проекций перпендикулярно друг другу, что позволит легко переходить от изображения на плоскостях проекций к реальному объекту в пространстве.
Таким образом, наложив эти ограничения на метод центрального проецирования, мы пришли к его частному случаю – методу параллельного проецирования (Рисунок 1.3).Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P, называется параллельным.
Рисунок 1.3 – Метод параллельного проецирования
Введём обозначения:
Введём обозначения:
Р – направление проецирования;
π1 – горизонтальная плоскость проекций;
A, B – объекты проецирования – точки;
А1 и В1 – проекции точек А и В на плоскость проекций π1.
Параллельной проекцией точки называется точка пересечения проецирующей прямой, параллельной заданному направлению проецирования Р, с плоскостью проекций π1.
Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р. Проецирующий луч проведённый через точку А пересечёт плоскость проекций π1 в точке А1. Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В1. Соединив точки А1 и В1, получим отрезок А1 В1– проекция отрезка АВ на плоскость π1.
1.3. Ортогональное проецирование. Метод Монжа
Если направление проецирования Р перпендикулярно плоскости проекций p1, то проецирование называется прямоугольным (Рисунок 1.4), или ортогональным (греч. ortos – прямой, gonia – угол), если Р не перпендикулярно π1, то проецирование называется косоугольным.
Четырехугольник АА1В1В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π1 (γ⊥π1). В дальнейшем будем использовать только прямоугольное проецирование.
Рисунок 1.4 – Ортогональное проецирование
Рисунок 1.5- Монж, Гаспар (1746-1818)
Основоположником ортогонального проецирования считается французский учёный Гаспар Монж (Рисунок 1.5).
До Монжа строители, художники и учёные обладали довольно значительными сведениями о проекционных способах, и, всё же, только Гаспар Монж является творцом начертательной геометрии как науки.
Гаспар Монж родился 9 мая 1746 года в небольшом городке Боне (Бургундия) на востоке Франции в семье местного торговца. Он был старшим из пяти детей, которым отец, несмотря на низкое происхождение и относительную бедность семьи, постарался обеспечить самое лучшее образование из доступного в то время для выходцев из незнатного сословия. Его второй сын, Луи, стал профессором математики и астрономии, младший — Жан также профессором математики, гидрографии и навигации. Гаспар Монж получил первоначальное образование в городской школе ордена ораторианцев. Окончив её в 1762 году лучшим учеником, он поступил в колледж г. Лиона, также принадлежавший ораторианцам. Вскоре Гаспару доверяют там преподавание физики. Летом 1764 года Монж составил замечательный по точности план родного города Бона. Необходимые при этом способы и приборы для измерения углов и вычерчивания линий были изобретены самим составителем.
Во время обучения в Лионе получил предложение вступить в орден и остаться преподавателем колледжа, однако, вместо этого, проявив большие способности к математике, черчению и рисованию, сумел поступить в Мезьерскую школу военных инженеров, но (из-за происхождения) только на вспомогательное унтер-офицерское отделение и без денежного содержания. Тем не менее, успехи в точных науках и оригинальное решение одной из важных задач фортификации (о размещении укреплений в зависимости от расположения артиллерии противника) позволили ему в 1769 году стать ассистентом (помощником преподавателя) математики, а затем и физики, причём уже с приличным жалованием в 1800 ливров в год.
В 1770 году в возрасте 24-х лет Монж занимает должность профессора одновременно по двум кафедрам — математики и физики, и, кроме того, ведёт занятия по резанию камней. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке – начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года, книга вышла под названием Начертательная геометрия (Géométrie descriptive) (стенографическая запись этих лекций была сделана в 1795 году). Изложенный в ней подход к чтению лекций по этой науке и выполнению упражнений сохранился до наших дней. Еще один значительный труд Монжа – Приложение анализа к геометрии (L’application de l’analyse à la géometrie, 1795) – представляет собой учебник аналитической геометрии, в котором особый акцент делается на дифференциальных соотношениях.
В 1780 был избран членом Парижской академии наук, в 1794 стал директором Политехнической школы. В течение восьми месяцев занимал пост морского министра в правительстве Наполеона, заведовал пороховыми и пушечными заводами республики, сопровождал Наполеона в его экспедиции в Египет (1798–1801). Наполеон пожаловал ему титул графа, удостоил многих других отличий.
Метод изображения объектов по Монжу заключается в двух основных моментах:
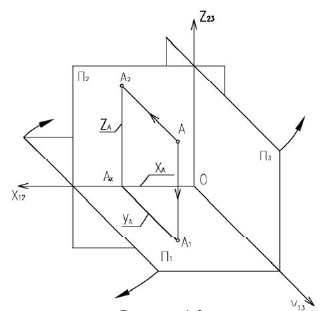
1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π1 и π2 (Рисунок 1.6).
Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие координатных осей проекций на линию пересечения плоскостей проекций (ось проекций) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.
Рисунок 1.6 – Модель построения проекций точки
π1 – горизонтальная (первая) плоскость проекций
π2 – фронтальная (вторая) плоскость проекций
π1∩π2 — ось проекций (обозначим π2/π1)
Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π1 и π2.
Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π1 и π2 и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А1 – горизонтальная (первая) проекция точки А;А2 – фронтальная (вторая) проекция точки А; АА1 и АА2 – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π1 и π2. Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π1 и π2:
АА1⊥π1
А2А0⊥π2/π1 АА1 = А2А0 — расстояние от точки А до плоскости π1
АА2⊥π2
А1А0⊥π2/π1 АА2 = А1А0 — расстояние от точки А до плоскости π2
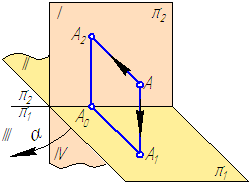
2. Совместим поворотом вокруг оси проекций π2/π1 плоскости проекций в одну плоскость (π1 с π2), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным (ортогональным) чертежом (Рисунок 1.7):
Рисунок 1.7 – Ортогональный чертеж
Прямоугольный или ортогональный носит название эпюр Монжа.
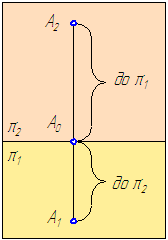
Прямая А2А1 называется линией проекционной связи, которая соединяет разноимённые проекции точки (А2 — фронтальную и А1 — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А2А1⊥π2/π1. На эпюре отрезки, обозначенные фигурными скобками, представляют собой:
- А0 А1 – расстояние от точки А до плоскости π2, соответствующее координате yА;
- А0 А2 – расстояние от точки А до плоскости π1, соответствующее координате zА.
1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа
1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.
2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.
Убедимся в справедливости последнего утверждения, для чего повернём плоскость π1 в исходное положение (когда π1⊥π2). Для того, чтобы построить точку А необходимо из точек А1 и А2 восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π1и π2, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).
Рисунок 1.8 – Построение эпюра точки
Введём третью (профильную) плоскость проекций π3 перпендикулярную π1 и π2 (задана осью проекций π2/π3).
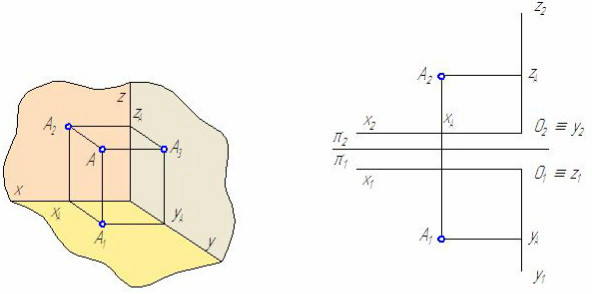
Расстояние от профильной проекции точки до вертикальной оси проекций А‘0A3 позволяет определить расстояние от точки А до фронтальной плоскости проекций π2. Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A(XA; YA; ZA) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A1=(XA; YA); A2=(XA; ZA)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).
а б
Рисунок 1.9 – Построение эпюра точки по её координатам
По расположению на эпюре проекций точки можно судить о её расположении в пространстве:
- если на эпюре горизонтальная проекция точки А — А1 лежит под осью координат X , а фронтальная — А2 – над осью X, то можно говорить, что точка А принадлежит 1-му квадранту;
- если на эпюре горизонтальная проекция точки А — А1 лежит над осью координат X, а фронтальная — А2 – под осью X, то точка А принадлежит 3-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат над осью X, то точка А принадлежит 2-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат под осью X, то точка А принадлежит 4-му квадранту;
- если на эпюре проекция точки совпадает с самой точкой, то значит – точка принадлежит плоскости проекций;
- точка, принадлежащая плоскости проекций или оси проекций (оси координат), называется точкой частного положения.
Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.
| X | Y | Z | |
|---|---|---|---|
| I | + | + | + |
| II | + | — | + |
| III | + | — | — |
| IV | + | + | — |
Упражнение
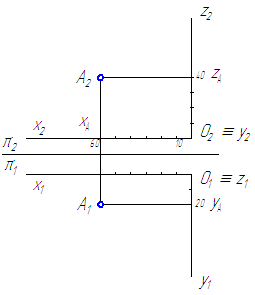
Построить ортогональные проекции точки с координатами А (60, 20, 40) и определить в каком квадранте расположена точка .
Решение задачи: по оси OX отложить значение координаты XA=60, затем через эту точку на оси OX восстановить линию проекционной связи, перпендикулярную к OX, по которой вверх отложить значение координаты ZA=40, а вниз – значение координаты YA=20 (Рисунок 1.10). Все координаты положительные, значит точка расположена в I квадранте.
Рисунок 1.10 – Решение задачи
1.5. Задачи для самостоятельного решения
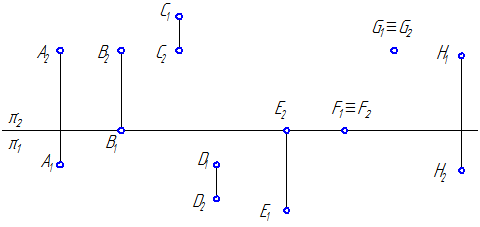
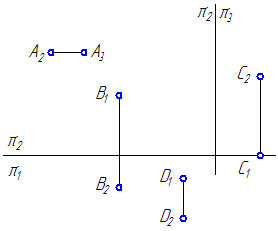
1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).
Рисунок 1.11
2. Достройте недостающие ортогональные проекции точек А, В, С на плоскости проекций π1, π2, π3 (Рисунок 1.12).
Рисунок 1.12
3. Постройте проекции точки:
- Е, симметричной точке А относительно плоскости проекций π1;
- F, симметричной точке В относительно плоскости проекций π2;
- G, симметричной точке С относительно оси проекций π2/π1;
- H, симметричной точке D относительно биссекторной плоскости второго и четвертого квадрантов.
4. Постройте ортогональные проекции точки К, расположенной во втором квадранте и удаленной от плоскостей проекций π1 на 40 мм, от π2 — на 15 мм.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Положение
точки в пространстве
Положение
точки в пространстве представим с
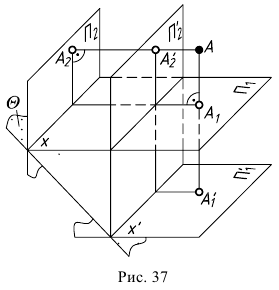
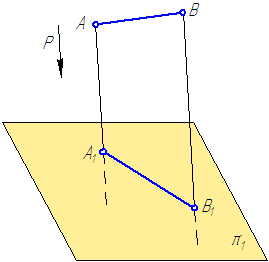
помощью пространственного макета. Пусть
даны в пространстве точка A и три
взаимно перпендикулярные плоскости
проекции.
Построим
проекции точки А, расположенной в первом
октанте пространства. Для этого через
точку проведем проецирующие лучи, идущие
перпендикулярно плоскостям проекций
. На пересечении этих лучей с плоскостями
проекций H, V, W находятся проекции
самой точки А (A`, A», A»`).
Положение
точки в пространстве
Положение
точки в пространстве определяется
тремя координатами (x, y, z), показывающими
величины расстояний, на которые она
удалена от плоскостей проекций.
Чтобы
определить эти расстояния, достаточно
через точку A провести прямые,
перпендикулярные к плоскостям проекций,
определить точки A`, A», A»` встречи
этих прямых с плоскостями проекций и
измерить величины отрезков [AA`], [AA»],
[AA»`], которые укажут соответственно
значение аппликаты z, ординаты y,
абсциссы x точки A.
Точки A`,
A», A»` называют ортогональными
проекциями точки A, при этом согласно
принятым обозначениям:
A` —
горизонтальная проекция точки A;
A» —
фронтальная проекция точки A;
A»` —
профильная проекция точки A.
Отрезки:
[AA`]
— [OAx] — абсцисса точки A;
[AA»] — [OAy] —
ордината точки A;
[AA»`] — [OAz] —
аппликата точки A.
Прямые
(AA` ⊥ H),
(AA» ⊥ V),
(AA»` ⊥ W)
называют проецирующими
прямыми или проецирующими
лучами.
Прямую (AA`), проецирующую
точку A на горизонтальную
плоскость проекций, называют горизонтально
проецирующей прямой (лучом).
Прямую
(AA») проецирующую точку A на фронтальную
плоскость проекций называют фронтально
проецирующей прямой (лучом).
Прямую
(AA»`) проецирующую точку A на профильную
плоскость проекций называют профильно-проецирующей
прямой (лучом).
Две проецирующие прямые,
проходящие через точку A, определяют
плоскость, которую принято называть
проецирующей.
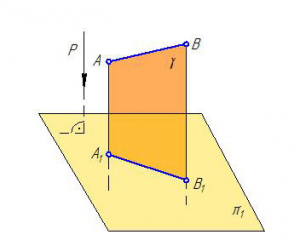
Чтобы
получить эпюр точки A, выполним
преобразование пространственного
макета в эпюр Монжа:
— фронтальная
проекция точки A остается на месте,
как принадлежащая плоскости V, которая
не меняет своего положения при
рассматриваемом преобразовании.
—
горизонтальная проекция A` вместе
с горизонтальной плоскостью проекции
опустится вниз и расположится на одном
перпендикуляре к оси x с фронтальной
проекцией A».
— профильная
проекция AA»` будет вращаться
вместе с профильной плоскостью проекции
и к концу преобразования займет положение,
указанное на рисунке. При этом AA»` будет
принадлежать перпендикуляру к оси z,
проведенному через A» и удалена
от оси z на такое же расстояние, на
какое горизонтальная проекция A` удалена
от оси x.
Положение
точки в пространстве
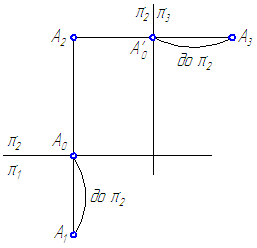
Связь
между горизонтальной и профильной
проекциями точки может быть установлена
с помощью двух ортогональных отрезков
[A`Ay] и [AyA»`] и сопрягающей их дуги
окружности, с центром в точке пересечения
координатных осей.
Отмеченной связью
пользуются для нахождения недостающей
профильной или горизонтальной проекции.
Положение
профильной (горизонтальной) проекции
по заданным горизонтальной (профильной)
и фронтальной проекциям может быть
найдено и без проведения дуги окружности.
В этом случае связь между горизонтальной
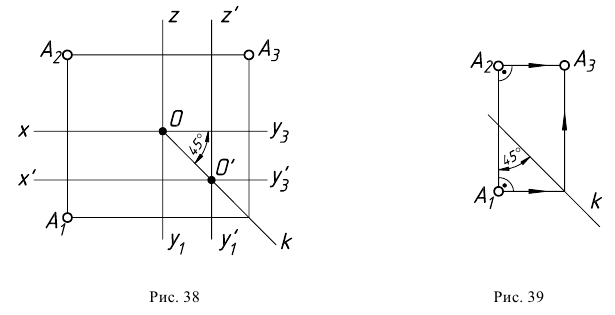
и профильной проекциями может быть
установлена с помощью ломаной
линии A`,Ao,A»` с вершиной Ao на
биссектрисе угла, образованного
осями y.
Биссектрису O,Ao,A»` называют
постоянной прямой ko эпюра Монжа.
Представленная
на рисунке плоская модель (эпюр) несет
такую же информацию, какая содержится
в пространственном макете.
Действительно:
чтобы определить положение точки в
пространстве, необходимо знать три
координаты точки A — (x, y, z) — это
длины отрезков [AA»`], [AA»], [AA`].
Величины
этих отрезков могут быть легко определены
на эпюре:
[AA»`] ≅
[A`Ay] ≅
[A»Az];
[AA»] ≅
[A`Ax] ≅
[A»`Az];
[AA`] ≅
[A»Ax] ≅
[A»`Ay].
Горизонтальная
проекция точки A определяется
абсциссой x и ординатой y
Фронтальная
проекция — абсциссой x и
аппликатой z
Профильная проекция
— ординатой y и аппликатой z
A[A`(x,
y); A»(x, z); A»`(y, z)]
Из
записи следует:
1. Точка в пространстве
удалена:
а) от плоскости проекции W на
такую же величину, на какую горизонтальная
проекция этой точки A` удалена от
оси y (или же фронтальная проекция A»
от оси z);
б) от плоскости проекции V на
такую же величину, на какую горизонтальная
проекция этой точки A` удалена от
оси x (или ее профильная проекция A»` от
оси z);
в) от плоскости проекции H на
такую же величину, на какую ее фронтальная
проекция A» удалена от оси x (или
ее профильная проекция A»` от
оси y).
2. Положение
точки в пространстве вполне определяется
положением ее двух ортогональных
проекций.
Как следствие из этого — по
двум любым заданным ортогональным
проекциям точки всегда можно построить
недостающую ее третью ортогональную
проекцию.
Действительно: какое бы
сочетание из двух ортогональных проекций
мы не взяли, они всегда дают нам значение
всех трех координат точки.
3. a)
горизонтальная и фронтальная проекции
любой точки принадлежат одному
перпендикуляру к оси x.
Если
принять во внимание, что на эпюре прямые,
перпендикулярные к осям проекций и
соединяющие разноименные проекции
точек, называют линиями связи (проекционной
связи), то пункт 3. а) может быть сформулирован
иначе:
горизонтальная и фронтальная
проекции любой точки принадлежат одной
линии связи.
б)
горизонтальная и профильная проекции
любой точки принадлежат одному
перпендикуляру (одной линии связи) к
оси y;
в) фронтальная и профильная
проекции любой точки принадлежат одному
перпендикуляру (одной линии связи) к
оси z
Соседние файлы в папке НГиИГ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #