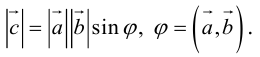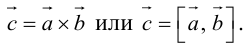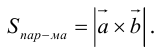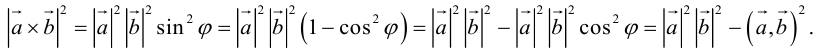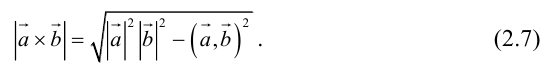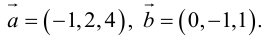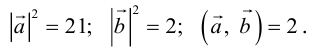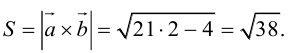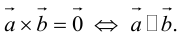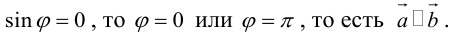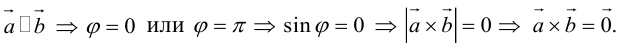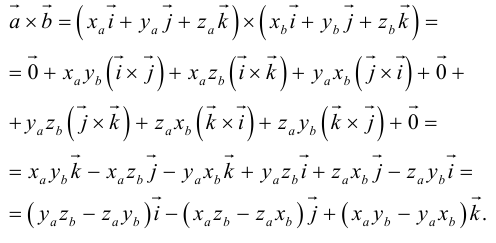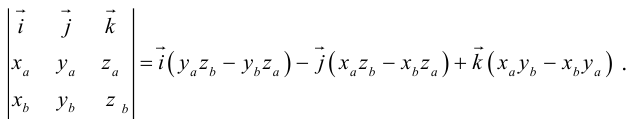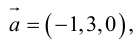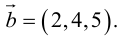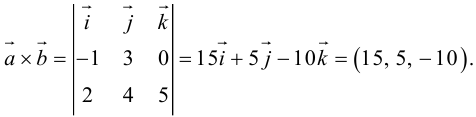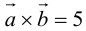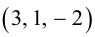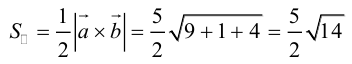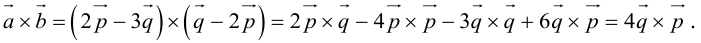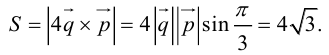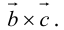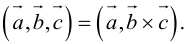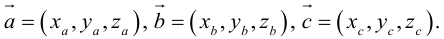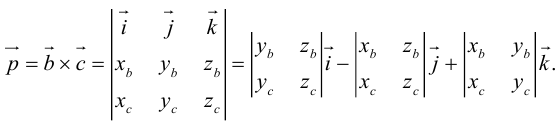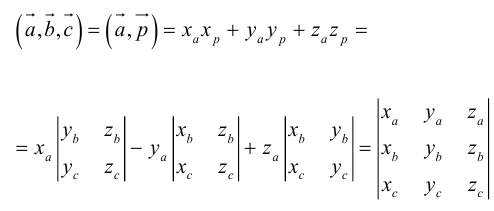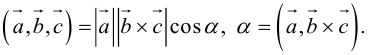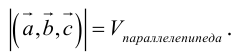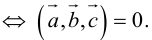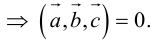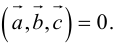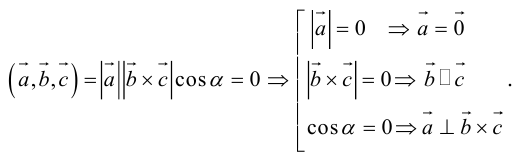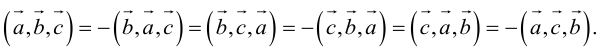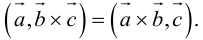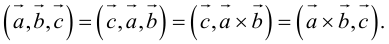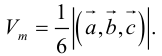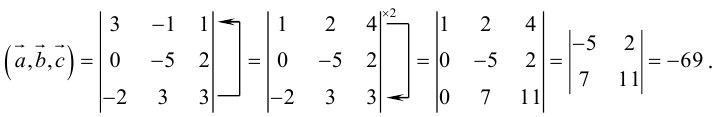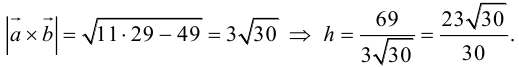Понятие
вектора
Определение
1. Вектором называется направленный
отрезок ( или, что то же, упорядоченная
пара точек).
Обозначают:
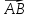
вектора) или одной буквой —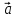
Определение
2. Длиной вектора (модулем)называется
расстояние между началом и концом
вектора. Длина вектора обозначается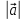
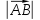
Определение
3. Нулевым вектором называется
вектор, у которого начало и конец
совпадают. Обозначают:
Определение
4. Единичным векторомназывается
вектор, длина которого равна единице.
Единичный
вектор, имеющий одинаковое направление
с данным вектором
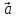
называется ортом вектора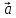
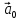
Определение
5. Векторы называютсяколлинеарными,
если они расположены на одной прямой
или на параллельных прямых. Нулевой
вектор считается коллинеарным любому
вектору.
Определение
6. Векторы называютсяравными,
если они коллинеарны, имеют одинаковые
длины и одинаковое направление.
Линейные
операции над векторами
Определение
7. Линейными операциями над вектораминазываются сложение векторов и умножение
вектора на число.
Определение
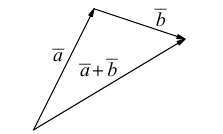
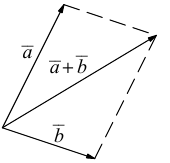
8. Суммой
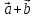
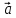

вектор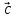
который идет из начала вектора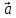
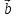
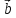
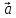
неколлинеарных векторов
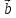
вместо правила треугольника использовать
правило параллелограмма: если векторы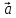
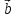
построен параллелограмм, то сумма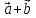
этого параллелограмма, идущего из общего
начала

Определение
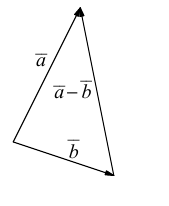
9. Разностью
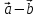
векторов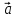
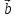
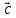
который в сумме с вектором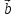
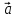
Если два вектора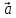
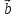
есть вектор, исходящий из конца вектора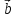

Определение
10. Два коллинеарных вектора равной
длины, направленные в противоположные
стороны, называются противоположными.
Вектор, противоположный вектору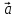
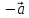
Произведение
вектора
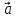
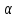
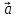
Некоторые
свойства линейных операций
1)
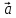
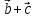
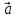
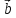
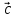
2)
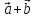
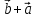
3)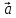
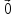

4)
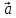
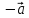
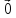
5)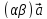

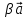
6)
7)


1·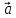
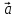
Теорема
1. (О коллинеарных векторах). Если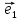

вектор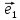
то существует единственное число х
такое, что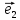
В
частности, ненулевой вектор
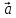
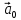

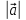
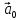
Сформулированные
свойства линейных операций позволяют
преобразовать выражения, составленные
из векторов, по обычным правилам алгебры:
можно раскрыть скобки, приводить подобные
члены, переносить некоторые члены в
другую часть равенства с противоположным
знаком и т.д.
Пример
1.
Доказать
равенства:
а)
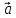
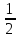


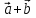
б)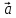
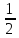

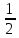
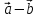
и
выяснить, каков их геометрический смысл.
Решение.
а) В левой части равенства раскроем
скобки, приведем подобные члены, получим
вектор в правой части. Поясним это
равенство геометрически. Пусть даны
два вектора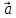
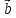
отложим их от общего начала и посмотрим
параллелограмм и его диагонали, получим:
§2 Линейная комбинация векторов
Векторный
базис на плоскости и в пространстве.
Определение
1. Линейной комбинацией векторов
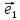
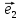
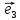
векторов на какие-нибудь числа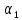
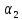

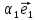
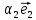
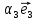
Определение
2. Векторным базисом в данной
плоскости называется любая пара
неколлинеарных векторов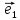
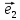
Вектор
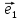
при этом первым базисным вектором,
вектор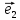
Справедлива
следующая теорема.
Теорема
1.Если базис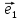
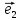
любой вектор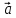
и притом единственным образом, в виде
линейной комбинации базисных векторов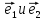
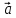
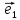
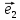
(*)
Определение
3. Равенство(*) называютразложением
вектора
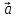
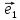
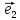
а числа х и у –координатами вектора
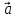
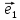
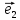
илиотносительно базиса

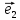
речь, то пишут кратко: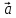
определения координат вектора относительно
базиса следует, что равные векторы имеют
соответственно равные координаты.
Два
и более векторов в пространстве называются
компланарными, если они параллельны
одной и той же плоскости или лежат в
этой плоскости.
Определение
4. Векторным базисом в пространстве
называют любые три вектора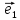

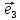
Вектор
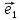
вектором,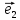
Замечание.
1. Три вектора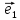
{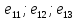
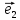
{
и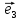

образуют базис пространства, если
определитель, составленный из их
координат, отличен от нуля :

2.
Основные положения теории определителей
и способы их вычисления рассмотрены в
модуле 1 «линейная алгебра».
Теорема
2. Пусть

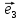
любой вектор
и притом единственным образом, в виде
линейной комбинации базисных векторов
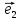
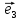
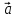
х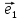
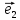
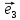
(**)
Определение
5. Равенство (**) называютразложением
вектора

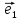
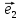

а числаx,y,z–координатами
(компонентами) вектора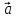
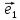
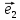
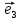
Если
заранее ясно, о каком базисе идет речь,
то пишут кратко:
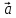
Определение
6. Базис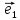
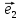
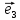
векторы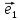
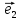
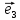
длину. В этом случае приняты обозначения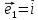
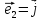
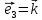
Действия
над векторами, заданными своими
координатами.
Теорема
3. Пусть на плоскости выбран векторный
базис
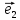
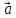
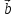
своими координатами: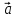

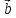
{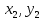
Тогда
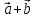
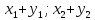
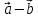
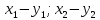
т.е. при сложении или вычитании векторов
складываются или вычитаются их одноименные
координаты;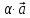
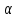
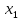
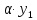
т.е. при умножении вектора на число его
координаты умножаются на это число.
Условие
коллинеарности двух векторов
Теорема
4. Вектор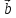
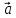
вектора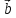
координатам вектора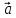
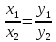
Линейные
операции над векторами, заданными своими
координатами в пространстве, производятся
аналогично.
Пример
1. Пусть даны векторы

= {1;0;1} в некотором векторном базисе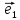

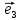
Найти координаты линейной комбинации
2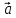
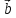
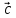
Решение.
Введем обозначение для линейной
комбинации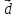
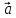

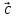
Коэффициенты
линейной комбинации
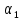
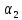

Запишем данное векторное равенство в
координатной форме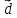
{x,y,z}=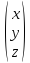
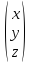
Очевидно,
что каждая координата линейной комбинации
векторов равна такой же линейной
комбинации одноименных координат, т.е.
х
= 2·1+3·3+(-4)·1=7,
у
= 2·2+3·2+(-4)·0=10,
z= 2·(-1)+3·1+(-4)·0=-3.
Координаты
вектора
в базисе
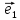
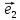
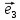

{7,10,-3}
Ответ: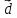
{7,10,-3}.
Общая
(аффинная) декартова система координат
Определение
7. Пусть О- некоторая фиксированная
точка, которую будем называтьначалом.
Если
М- произвольная точка, то вектор
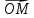
М по отношению к началу, коротко,
радиус-вектор точки М.
Декартовы
(аффинные) координаты на прямой
Пусть
дана в пространстве некоторая прямая
l.Выберем начало
О лежащим на этой прямой. Кроме того,
выберем на прямойl
ненулевой вектор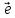
который будем называть базисным.
Определение
8. Пусть точка М лежит на прямойl.
Так как векторы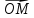
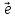
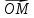

где х- некоторое число. Это число назовемкоординатой точки М на прямой.
Начало
О имеет положительные или отрицательные
координаты, в зависимости от того,
совпадают ли направления векторов
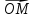
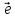
на которой координаты, будем называть
осью координат или осью ОХ.
Введение
координат на прямой соответствует
единственное число х, и наоборот,
существует единственная точка М, для
которой это число является координатой.
Декартовы
(аффинные) координаты на плоскости.
Выберем
на плоскости О два неколлинеарных
вектора
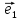
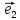
образующих некоторый базис . Очевидно,
что длины векторов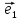
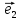
Определение
9. Совокупность {0;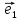
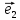
точки О и векторного базиса

декартовой (аффинной) системой на
плоскости.
Две
прямые, проходящие через О и параллельные
соответственно векторам
осями координат. Первую из них обычно
называют осью абсцисс и обозначают Ох,
вторую- осью ординат и обозначают Оу.
Будем
всегда изображать
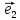
координат.
Определение
10. Координатами точки М на плоскости
относительно декартовой (аффинной)
системы координат {0;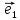
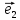
называют координаты ее радиус-вектора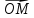
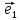
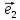
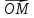
х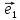
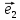
тогда числа х и у будет координатами М
относительно декартовой(аффинной)
системы координат {0;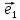
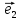
Координату х называютабсциссой точки
М, координату у-ординатой точки М.
Итак,
если выбрана система координат, {0;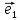
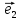
на плоскости, то каждой точке М плоскости
соответствует единственная точка М на
плоскости: эта точка является концом
вектора

х

Введение
системы координат лежит в основе метода
аналитической геометрии, сущность
которой состоит в том, чтобы уметь
сводить любую геометрическую задачу к
задачам арифметики или алгебры.
Определение
11. Координатами вектора
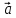
плоскости относительно декартовой
системы координат {0;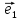
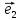
называют координаты этого вектора в
базисе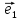
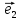
Чтобы
найти координаты вектора
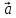
надо разложить его по базису

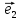
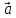
х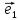
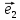
где коэффициенты х,у и будут координатами
вектора
относительно декартовой системы {0;

Декартова
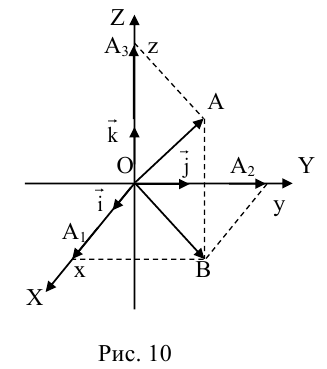
(аффинная) система координат в пространстве.
Пусть
в пространстве зафиксирована некоторая
точка О(начало) и выбран векторный базис

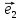
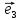
Определение
12. Совокупность {0;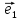
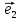
пространстве.
Определение
13. Три прямые проходящие через О и
параллельные соответственно векторам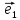
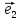
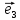
называютосями координат и обозначают
соответственно Оz,Oy,Oz.Мы
будем всегда изображать векторы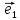
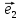
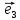
Определение
14. Координатами точки М в пространстве
относительно декартовой системы
координат {0;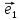
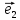
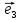
называют координаты ее радиус-вектора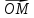
Иначе
говоря, координаты точки М – это такие
три числа х,у,zсоответственно
абсцисса и ордината точки М; третью
координатуzназывают
аппликатой точки М.
Введение
в пространстве декартовой системы
координат позволяет установить
взаимно-однозначное соответствие между
точками М пространства и упорядоченными
тройками чисел x,y,z.
Определение
15. Координатами вектора
в пространстве относительно декартовой
системы координат {0;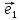
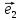
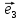
координаты этого вектора в базисе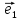
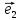
Пример
2.
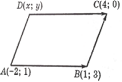
Даны
три последовательные вершины
параллелограмма А(-2;1),В(1;3),С(4;0). Найти
четвертую его координату D.
Система координат аффинная.
Решение.
Векторы

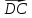
коэффициенты линейной комбинации):
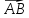
{3;2},


Значит,D(1;-2).
Ответ:D(1;-2).
Линейная
зависимость. Понятие базиса
Определение
16. Векторы
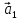

линейно зависимыми, если
существуют числа
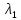
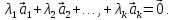
Это
определение линейной зависимости
векторов
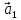
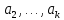
такому: векторы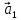
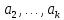
представить в виде линейной комбинации
остальных (или разложить по остальным).
Векторы
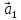
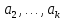
равенство (***) возможно в единственном
случае, когда
Понятие
линейной зависимости играет большую
роль в линейной алгебре. В векторной
алгебре линейная зависимость имеет
простой геометрический смысл.
-
Любые
два коллинеарных вектора линейно
зависимы, и наоборот, два неколлинеарных
вектора линейно независимы. -
Три
компланарных вектора линейно зависимы,
и наоборот, три некомпланарных вектора
линейно независимы. -
Каждые
четыре вектора линейно зависимы.
Определение
17. Три линейно
независимых вектора
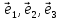
пространства, т.е.
любой вектор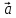
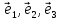
Определение
18. Два лежащих
в плоскости линейно независимых вектора
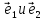
плоскости, т.е.
любой лежащий в этой плоскости вектор
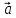
комбинации векторов
Задания
для самостоятельного решения.
-
Даны
три вектора
Найти
разложение векторапо
базису -
Даны
векторы
Вектор
–медиана
треугольникаOAB.
Разложить вектор
по
базису -
В
тетраэдре OABC
точки K,
L,
M,
N,
P,
Q
– середины рёбер OA,
OB,
OC,
AB,
AC,
BC
соответственно, S
– точка пересечения медиан треугольника
ABC.
Принимая за базисные
векторы
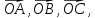
-
векторов
-
векторов
-
векторов
и
-
Точки
Mи
N
– середины сторон BCи
CDпараллелограмма
ABCD.
Разложить вектор
по
векторами
-
Дан
куб ABCDEFGH.
Разложить вектор
,
гдеK–
центр грани DHGC,
по векторам
,
-
На
плоскости даны вектора
Найти
разложение векторапо
базису,
-
На
плоскости даны три вектора
и
Определить разложение каждого из этих
трёх векторов, принимая в качестве
базиса два других. -
Принимая
в качестве базиса векторы
и
,
совпадающие со сторонами треугольникаABC,
определить разложение векторов,
приложенных в вершинах треугольника
и совпадающих с его медианами. -
Даны
четыре вектора
Найти координаты векторов – линейных
комбинаций: -
Даны
четыре вектора
,
Найти числа α, β, γ такие, что α
-
Проверить,
что векторы
образуют базис в пространстве. Найти
координаты векторов,
в
этом базисе. -
(Задача
об отрезке, разделённом в заданном
отношении.) Пусть точка C,
лежащая на отрезкеAB,
делит этот отрезок в отношении λ, т.е.
Выразить вектор
через векторы
и
-
Даны
две точки A(1;2;3).
B(7;2;5).
На прямой ABнайти
такую точку M,
чтобы точки Bи
Mбыли
расположены по разные стороны от точки
A и чтобы отрезок AMбыл
вдове длиннее отрезка AB.
Система координат аффинная. -
Вершина
Aпараллелепипеда
ABCD
принята за начало координат, а векторы
– за базисные векторы. Найти в этой
системе координаты всех вершин
параллелепипеда. -
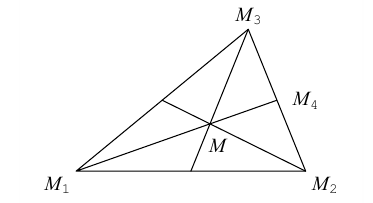
Вершина
Oтетраэдра
OABCDпринята
за начало координат, а векторы
– за базисные векторы. Найти на этой
(аффинной) системе координаты точек
пересечения медиан граней тэтраэдра.
Содержание
Линейные комбинации векторов в пространстве
Линейные комбинации векторов
Определение 1. Линейной комбинацией1) 


где 
Определение 2. Векторы 



Определение 3. Векторы 


Предложение 1. Если хотя бы один из векторов 
Предложение 2. Если среди 


Предложение 3. Система векторов линейно зависима тогда и только тогда, когда один из них представим в виде линейной комбинации остальных.
Обобщение понятия «линейная зависимость» можно посмотреть в соответствующей статье.
Линейная зависимость двух векторов
Предложение 4. Два вектора являются линейно зависимыми тогда и только тогда, когда они коллинеарны.
Линейная зависимость трех векторов
Предложение 5. Три вектора являются линейно зависимыми тогда и только тогда, когда они компланарны.
Линейная зависимость четырех векторов
Предложение 6. Любые четыре вектора в пространстве линейно зависимы.
Базис в пространстве, на плоскости и на прямой
Определение 4. Базисом в пространстве6) называется упорядоченная тройка некомпланарных векторов.
Определение 5. Базисом на плоскости7) называется пара неколлинеарных векторов, взятых в определенном порядке.
Определение 6. Базисом на прямой 
Определение 7. Пусть 

то говорят, что вектор 


Предложение 7.
-
Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой.
-
Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости.
-
Каждый вектор может быть разложен по базису в пространстве.
Координаты вектора в каждом случае определяются однозначно.
Предложение 8. При сложении векторов складываются их соответствующие координаты. При умножении вектора на число все его координаты умножаются на это число.
См. также
Литература
Наверх
Содержание:
Векторная алгебра
Векторная алгебра — это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая — конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор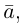
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 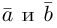
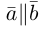
Аналогично, векторы а и b называются ортогональными (обозначение 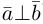
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
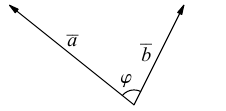
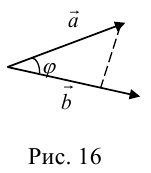
Углом между векторами 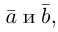
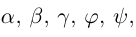
Два ненулевых вектора 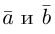
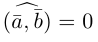
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 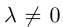
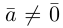
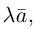
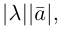
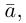
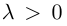
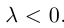
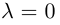
В частности, вектор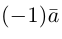
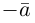
Если 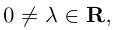
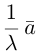
Из приведенного определения сразу же следует, что коллинеарные векторы 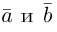
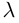
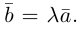
взять число 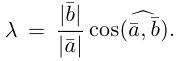
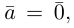
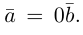
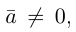
b) Сложение векторов.
Суммой двух векторов 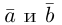
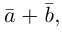
или по равносильному ему правилу параллелограмма
Вектор 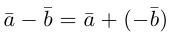
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 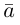
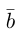
Геометрически очевидны следующие свойства проекции:
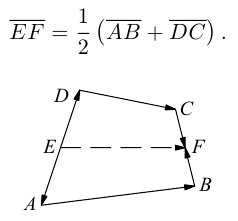
Пример №1
Пусть Е и F — середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 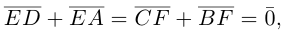
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 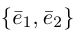
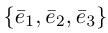
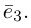
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 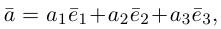
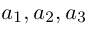
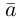
Приведем геометрическое доказательство этого утверждения.
Вектор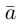
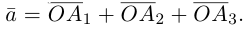
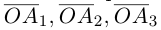
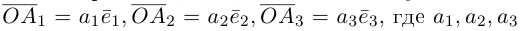
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 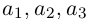
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 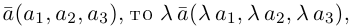
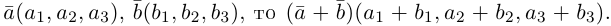
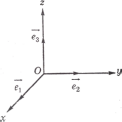
Рассмотрим теперь ортонормированный базис 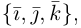
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 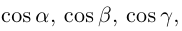
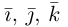
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 
В выбранной системе координат координаты радиуса-вектора 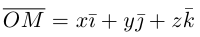
Если известны координаты начальной 
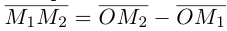
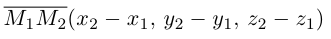
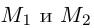
Найдем теперь координаты точки М, делящей отрезок с концами в точках 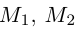
отношении 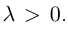
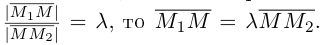
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
Треугольник задан координатами своих вершин 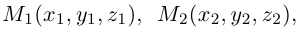
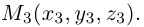
Пусть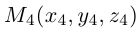
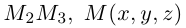
По известному свойству точки пересечения медиан 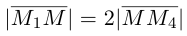
Подставив сюда найденные координаты точки 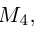
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 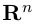
обладающая тем свойством, что любой вектор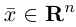
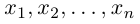
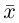
В качестве базиса в 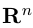
так как, очевидно, любой вектор 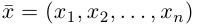
Скалярное произведение векторов
Определение: Скалярным произведением векторов 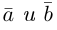
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое — из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 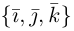
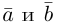
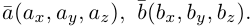
перемножим векторы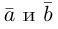
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 
Решение.
Из чертежа следует, что 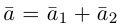
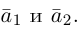
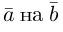
Тогда вторая ортогональная составляющая вектора 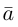
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 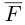
Найдем работу этой силы. Для этого разложим вектор силы 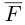
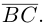
Составляющая 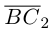
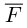
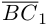
Окончательно, работа силы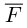
Замечание. Скалярным произведением векторов 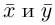
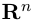
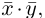
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 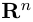
Длиной вектора 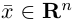
Векторы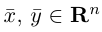
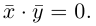
составляют ортонормированный базис пространства 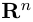
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 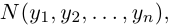
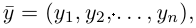
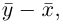
Таким образом переопределенное пространство 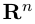
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R». Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
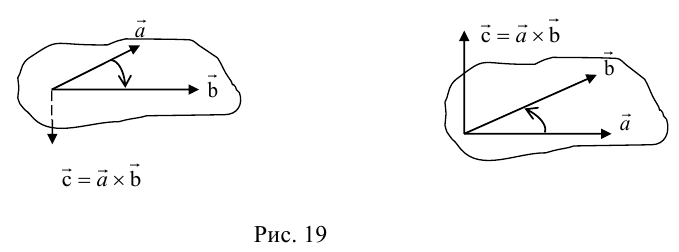
Определение: Векторным произведением некоялинеарных векторов 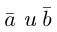

Из этого определения следует, что площадь параллелограмма, построенного на векторах 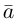
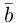

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 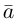
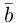
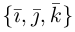
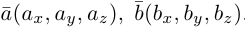
раскроем скобки в векторном произведении 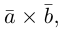
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 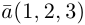
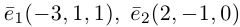
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 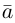

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 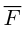
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 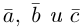
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 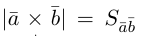
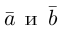
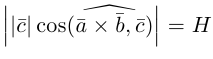
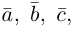
— объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 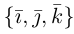
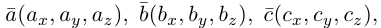
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 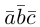
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 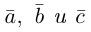
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 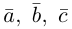
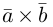
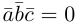
Следствие. Три вектора 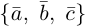
Заметим, кроме того, что, если 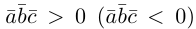
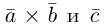
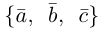
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 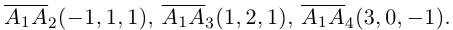
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 
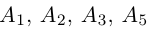
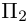
так как первая и третья строки в определителе пропорциональны. Плоскости 
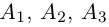
Векторы и линейные операции над ними
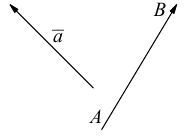
Определение: Вектором называется направленный отрезок (рис. 1).
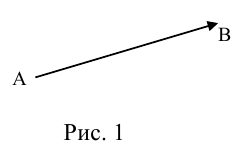
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 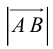
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
Определение: Векторы 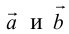
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
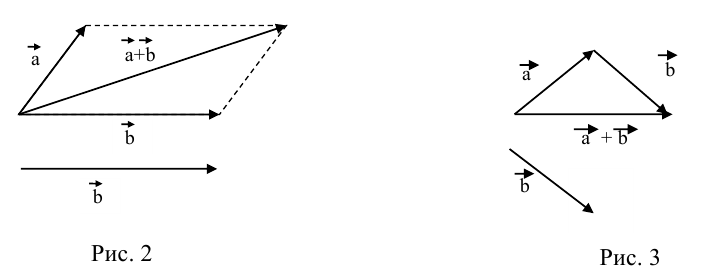
Сложение
а) Правило параллелограмма (рис.2): начала 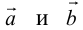
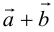
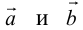
б) Правило треугольника (рис. 3): начало 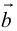
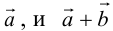
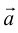
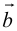
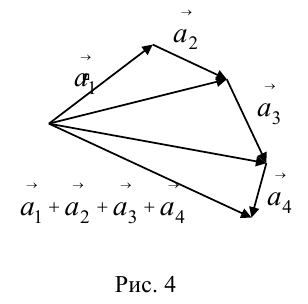
в) Правило сложения нескольких векторов (рис. 4).
Вектор 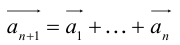
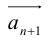
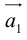
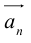
Умножение на число
Определение: Произведением вектора 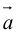
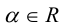
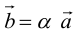
а) 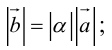
б) 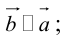
в)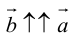
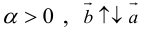
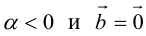
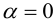
Произведение 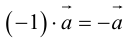
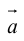
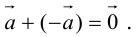
Определение: Разностью 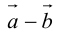
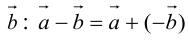
Начала 
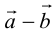
Свойства линейных операций
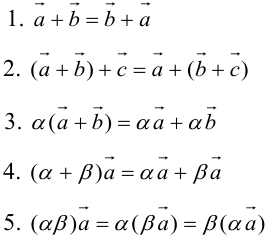
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: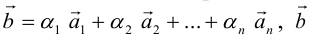
Пример №6
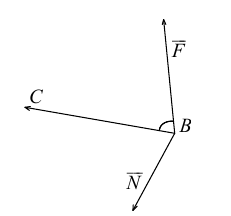
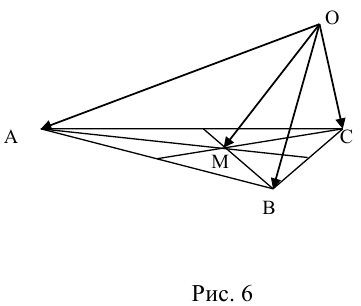
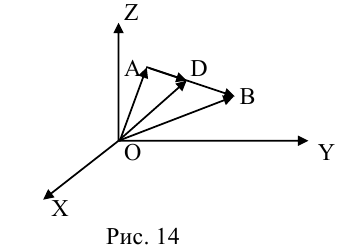
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 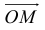
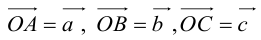
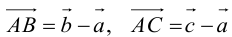
По правилу треугольника 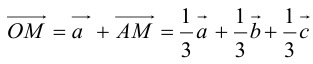
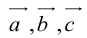
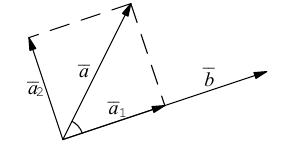
Теорема: Пусть 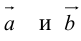
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 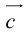
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
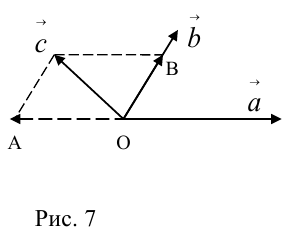
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 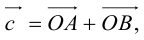
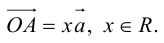
Докажем единственность разложения. Предположим, что 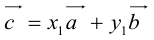
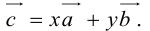
Если 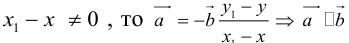
Теорема: Пусть 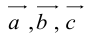
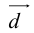
причем единственным образом.
Представление вектора 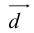
Доказать самостоятельно.
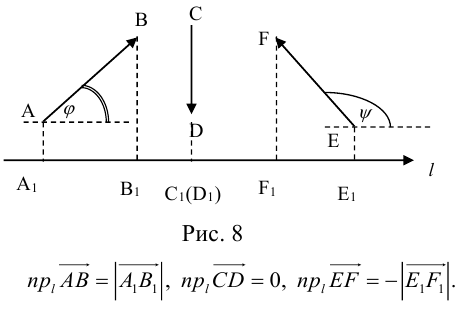
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 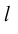
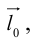
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 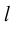
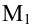
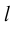
Определение: Ортогональной проекцией вектора 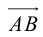
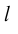
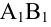
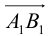
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
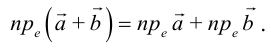
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 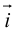
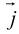

Аналогично в пространственной системе OXYZ 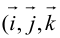
– разложение 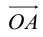
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 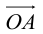
Определение: Координатами вектора 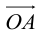
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 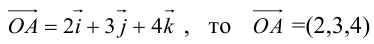
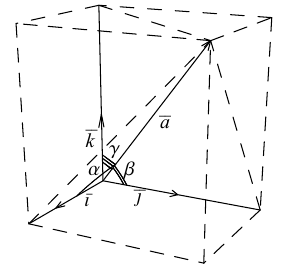
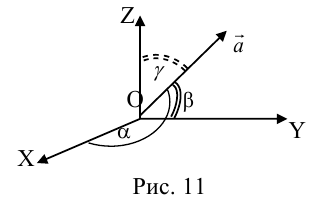
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 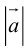
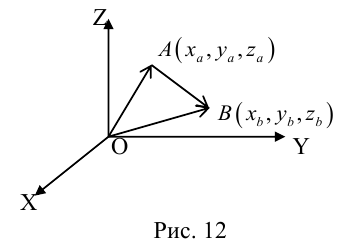
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
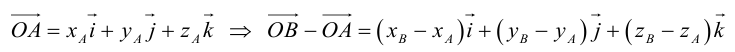
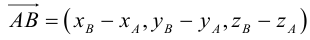
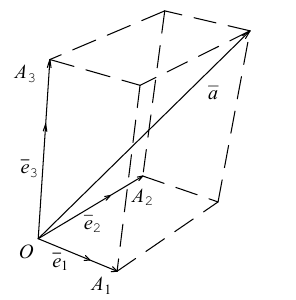
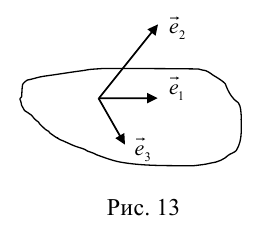
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 
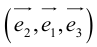
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 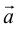
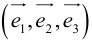
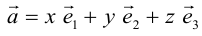
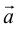
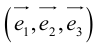
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 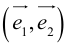
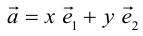
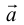
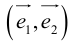
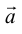
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 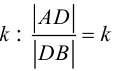
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
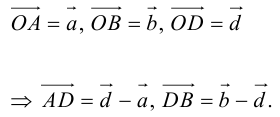
Так как 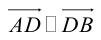
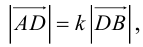
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
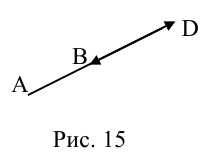
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 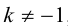
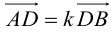
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 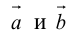
Скалярное произведение обозначается так: 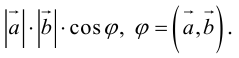
Так как 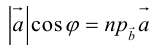
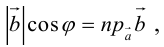
Свойства скалярного произведения
1.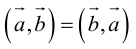
2.
Доказательство:
3.
Доказательство:
а) 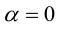
б)
в) 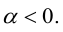
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 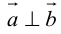
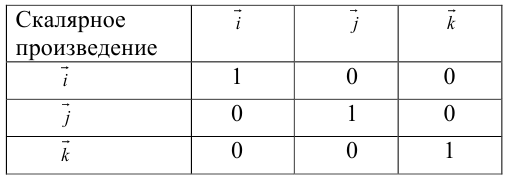
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 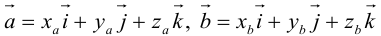
Таким образом,
Пример №8
Найти, при каком значении x векторы 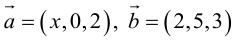
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 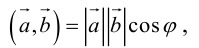
то
Найдем координаты векторов 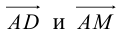
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 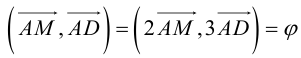
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 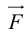
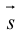
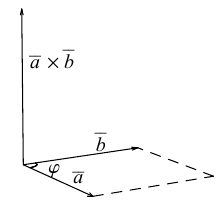
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 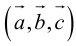
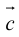
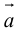
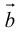
Определение: Векторным произведением вектора 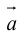
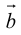
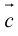
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 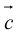
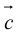
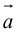
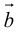
Свойства векторного произведения
1.
Доказательство:
а)пусть 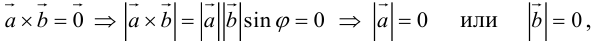
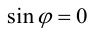
Его направление не определено, поэтому можно считать, что 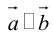
б)пусть
2. 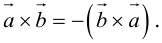
Доказательство: По определению направления векторов 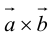
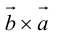
3.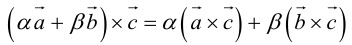
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 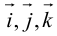
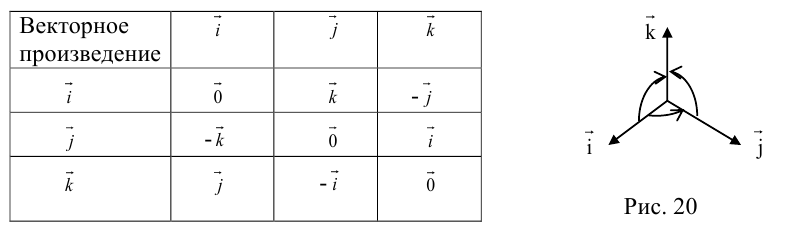
Пусть в некоторой пдск 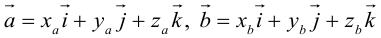
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 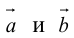
или
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 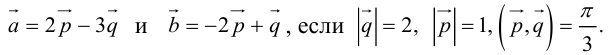
Так как 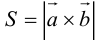
Отсюда
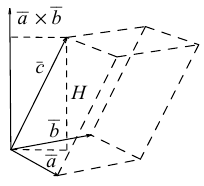
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 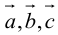
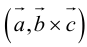
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
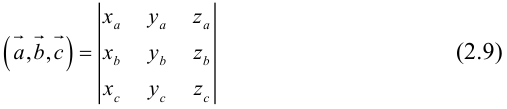
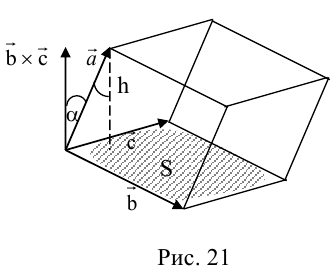
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
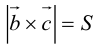
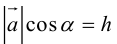
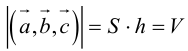
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 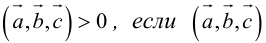
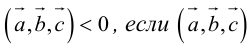
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 
Доказательство: а) 
Если 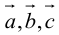
б)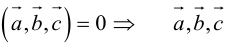
Во всех трех случаях 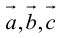
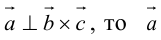
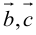
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
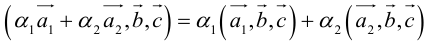
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
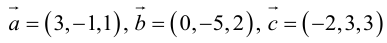
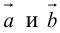
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 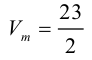
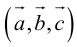
Чтобы найти высоту, воспользуемся формулой
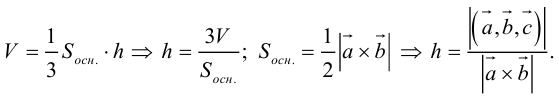
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Линейные операции над векторами в координатной форме
Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.
1. Равные векторы имеют равные координаты (в одном и том же базисе).
2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.
3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.
4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.
Докажем, например, последнее свойство. Проекция линейной комбинации векторов на прямую, содержащую базисный вектор , равна линейной комбинации проекций векторов (составляющих линейную комбинацию) на эту прямую. Поэтому абсцисса линейной комбинации векторов равна линейной комбинации абсцисс этих векторов. Аналогичное рассуждение справедливо для ординат и аппликат.
Замечания 1.7
1. Основные теоремы 1.3-1.5 о разложении вектора по базису устанавливают взаимно однозначное соответствие между множеством векторов пространства и множеством их координат в данном базисе. А именно, между векторами на прямой и действительными числами, между векторами на плоскости и упорядоченными парами чисел, между векторами пространства и упорядоченными тройками чисел. Например, при фиксированном базисе вектору
однозначно соответствует упорядоченная тройка чисел
, и наоборот, каждой упорядоченной тройке чисел
соответствует вектор
, т.е.
. В частности, если вектор
в базисе
имеет разложение
, то этому вектору соответствует тройка чисел
и наоборот. Нулевому вектору в любом базисе в пространстве соответствует нулевая тройка
.
2. Взаимно однозначное соответствие
(вектор) (его координаты)
сохраняет линейные операции: сумме векторов соответствует сумма их одноименных координат, произведению вектора на число соответствует произведение его координат на это число. Такое взаимно однозначное соответствие называется изоморфизмом.
3. На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
В базисе вектору
соответствует координатный столбец
.
Обозначение базиса можно не указывать, если не может возникнуть неоднозначности. Линейным операциям над векторами соответствуют линейные операции над их координатными столбцами. Например, если в одном и том же базисе
векторам
и
соответствуют координатные столбцы
и
, то их линейной комбинации
соответствует координатный столбец
, т.е. координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов.
Пример 1.10. Векторы и
относительно базиса
имеют координаты:
и
. Требуется найти координаты векторов
относительно того же базиса.
Решение. Запишем разложения по базису заданных векторов:
Используя свойства линейных операций, находим разложения по базису искомых векторов:
Следовательно, векторы имеют координаты:
соответственно.
Вычислим искомые координаты, используя матричную форму записи (см. пункт З замечаний 1.7). Векторам и
(в заданном базисе) соответствуют координатные столбцы
Находим координатные столбцы векторов
Как видим, результаты совпадают.
Пример 1.11. Известны разложения векторов ;
;
относительно базиса
на плоскости.
Разложить вектор : а) по векторам
и
; б) по векторам
и
.
Решение. а) Требуется представить вектор в виде линейной комбинации векторов
и
:
. Подставим в это равенство заданные разложения векторов:
. Приводя подобные члены в правой части, имеем
. Так как обе части равенства это разложения равных векторов по одному и тому же базису, то можно приравнять соответствующие координаты.
Получим систему уравнений
Решая систему, находим , т.е.
— искомое разложение.
б) Требуется представить вектор в виде линейной комбинации векторов
и
:
. Запишем это равенство в матричной форме
, заменив векторы их координатными столбцами:
которое равносильно системе уравнений
.
Эта система не имеет решения (прибавив к первому уравнению удвоенное второе, получим неверное равенство ). Следовательно, вектор
нельзя разложить по векторам
и
(заметим, что векторы
и
коллинеарны
, а вектор
не коллинеарен им).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

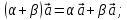
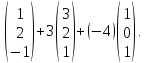




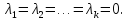
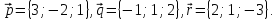 Найти
Найти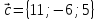 по
по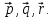
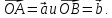 Вектор
Вектор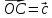 –медиана
–медиана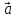 по
по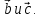

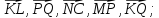
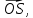 и
и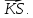
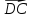 по
по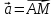 и
и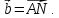
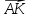 ,
,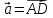 ,
,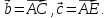
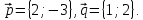 Найти
Найти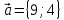 по
по ,
,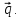
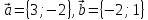 и
и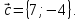 Определить разложение каждого из этих
Определить разложение каждого из этих и
и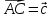 ,
,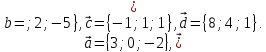 Найти координаты векторов – линейных
Найти координаты векторов – линейных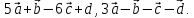
 ,
,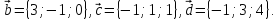 Найти числа α, β, γ такие, что α
Найти числа α, β, γ такие, что α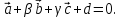
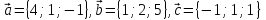 образуют базис в пространстве. Найти
образуют базис в пространстве. Найти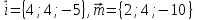 ,
,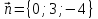 в
в Выразить вектор
Выразить вектор через векторы
через векторы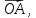 и
и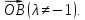

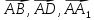
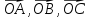 – за базисные векторы. Найти на этой
– за базисные векторы. Найти на этой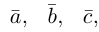
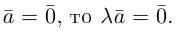
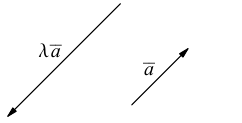
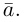
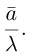
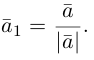
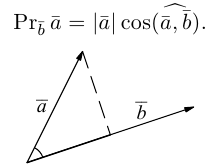
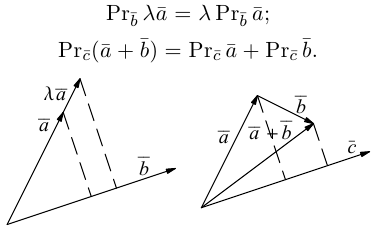
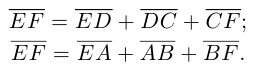
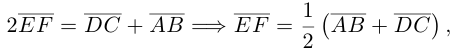
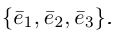
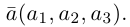
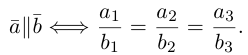
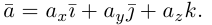
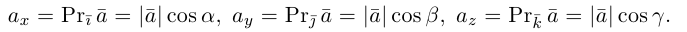
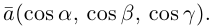
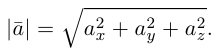

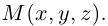
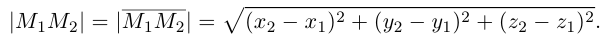
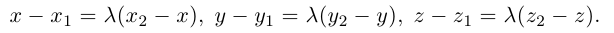
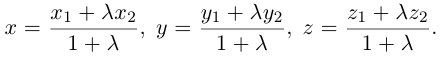
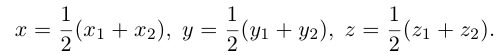
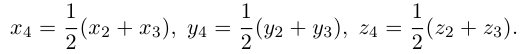
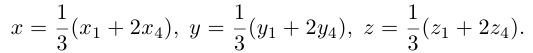
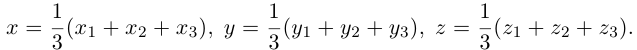


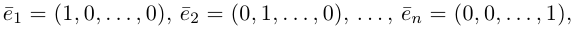
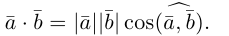
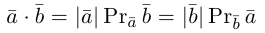
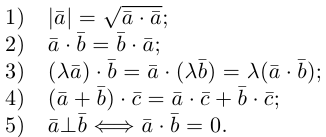
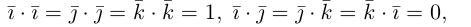
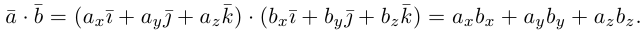
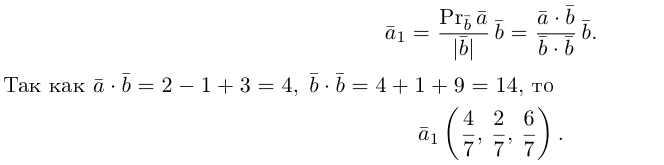
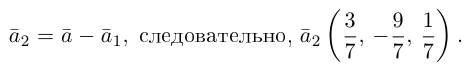
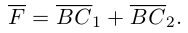
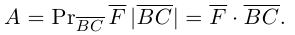
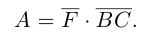
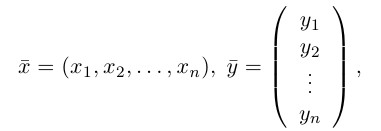
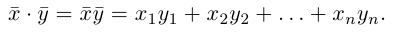
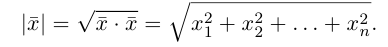
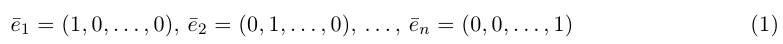

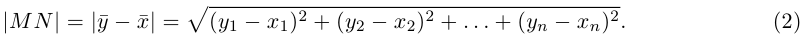
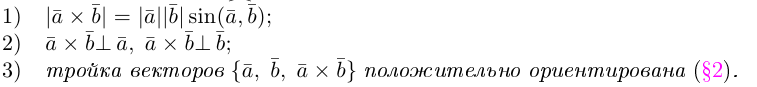
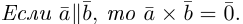
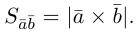
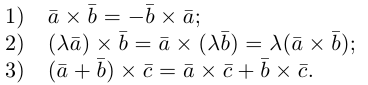
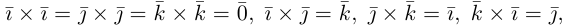
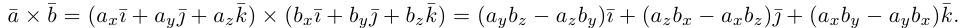
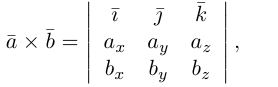
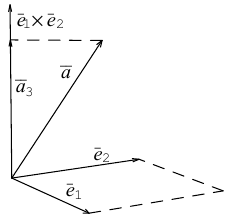
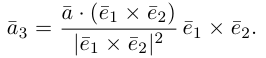
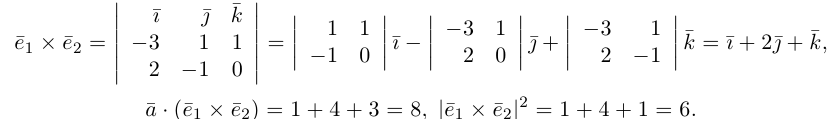
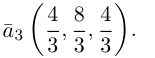
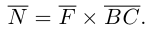
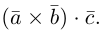
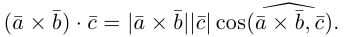
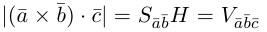
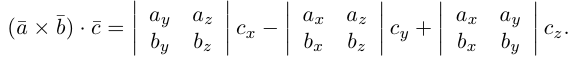
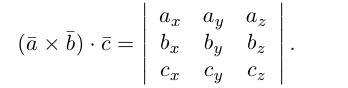
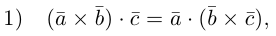
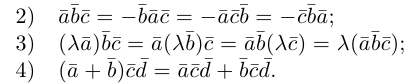
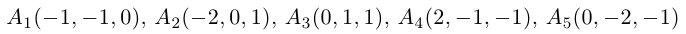
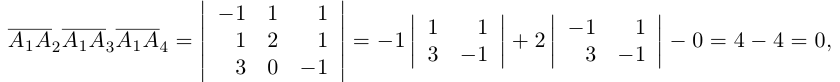
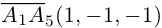
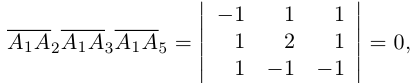
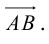

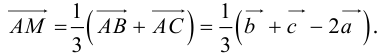
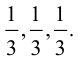
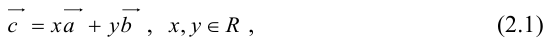
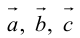 есть два коллинеарных, например:
есть два коллинеарных, например: 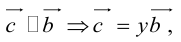
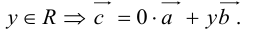
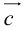 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 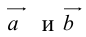 (рис. 7).
(рис. 7). 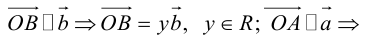
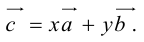
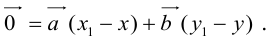
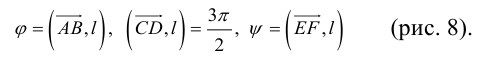
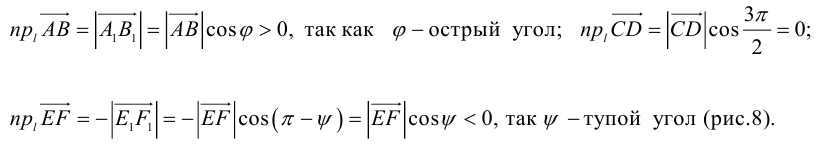
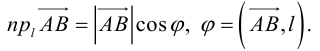
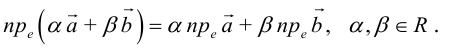
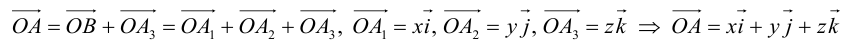
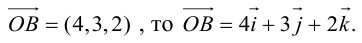
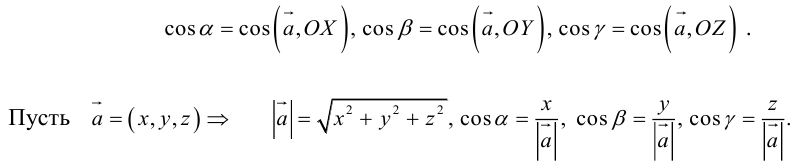
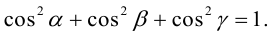
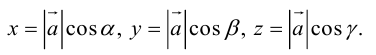
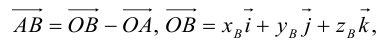
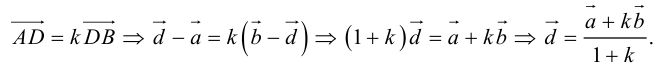
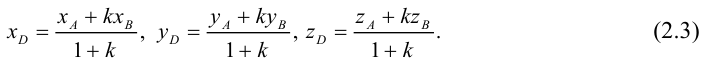
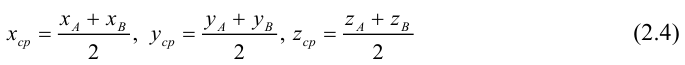
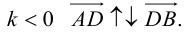
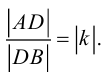
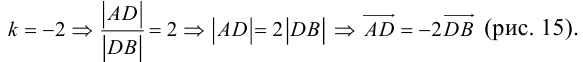
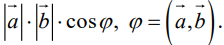
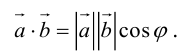
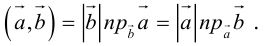
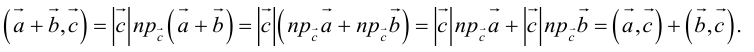
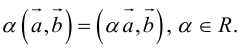
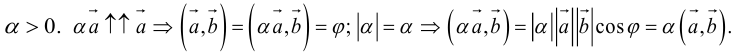
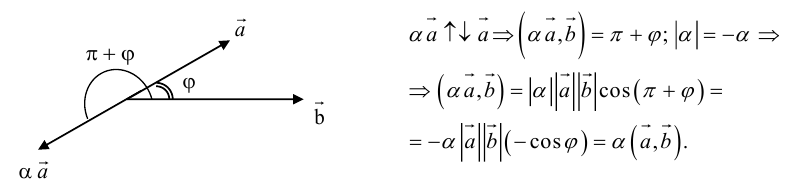
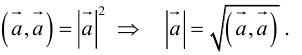
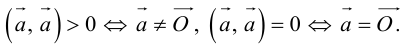
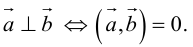
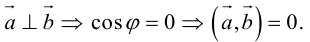
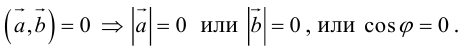
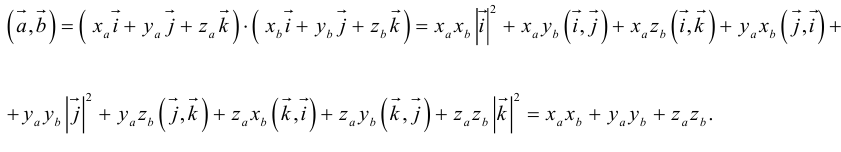

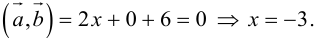
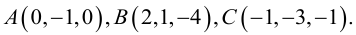

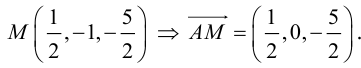
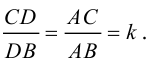
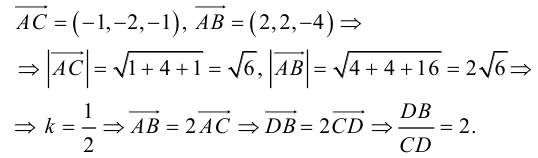
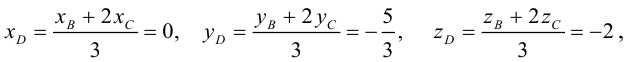
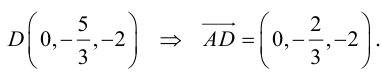
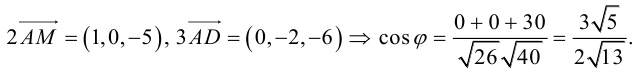
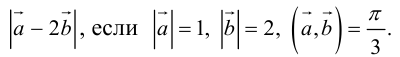
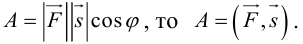
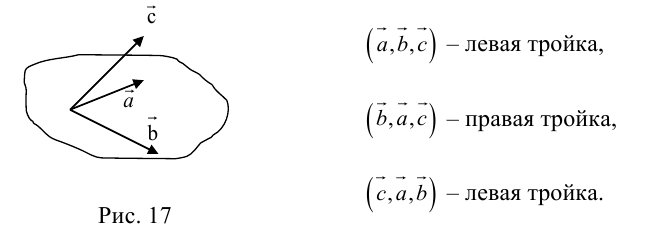
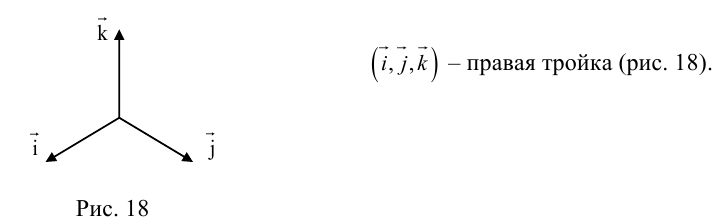
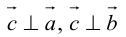 (
(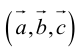 – правая.
– правая.