Как найти координаты центра поворота - AvtoShod.ru

Лучший ответ

ovod (75)

7 (86376)81875
13 лет

Взять пару соответствующих точек (т.е. одна на первой фигуре, а вторая образ этой точки на второй фигуре при повороте), соединить их отрезком и провести перпендикуляр к этому отрезку через его середину.

Сделать то же самое с другой парой соответствующих точек, выбранных так, чтобы соединяющий их отрезок не был параллелен первому отрезку.

Точка пересечения этих двух перпендикуляров и будет искомым центром поворота.

Ответы

StrangeManiac (33)

5 (4049)249
13 лет

На глазок

А чем строить не важно?

Проводим прямую через начальные точки двух отрезков $%AA’$%, из точки $%B$% проводим прямую параллельную полученной, из точки $%A’$% циркулем проводим дугу с радиусом $%A’B’$% до пересечения с прямой из точки $%B$%, получаем точку $%B’_1$%. Строим к прямой $%B’B’_1$% перпендикуляр через точку $%A’$%. Он по идее пройдёт через середину отрезка $%B’B’_1$%. Так же из середины отрезка $%AA’$% строим перпендикуляр. Точка пересечения перпендикуляров будет центром поворота, что можно легко проверить тем же циркулем.

Источник

Сегодня поговорим об единичной окружности 🧑‍🏫

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔

Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:

x=x0+r⋅cos δ

y=y0+r⋅sin δ

x0,y0 — координаты центра окружности;

r — радиус окружности;

δ —угол поворота радиуса вектора.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Источник

Есть прямоугольник, чьи вершины заданы левой верхней точкой (x₁, y₁) и правой нижней (x₂, y₂). Необходимо произвести вращение прямоугольника вокруг произвольной точки (x₀, y₀) на угол α и найти координаты всех вершин после поворота.

Теория

Используем аффинные матрицу поворота и матрицу переноса. Формулы для нахождения координат при повороте следующие:

Точка вокруг которой хотим повернуть изображение имеет координаты O (x₀, y₀) . Чтобы получить значение x и y для формул выше, необходимо их нормализовать.

Смещение D(x,y) определяет, куда хотим поместить точку вращения после поворота. В подавляющем большинстве случаев оно равно точке вращения.

Окончательный вид формул:

Интерактив

На интерактиве ниже работают только эти формулы. «Произвольная» точка вращения зазывно мигает. Дескать, можно таскать. За вершины «не-повернутого» серого прямоугольника также можно таскать, меняя тем самым исходные координаты. При изменении координат происходит масштабирование с таким расчетом, чтобы «влез» процесс поворота. Делать на всю ширь возможных орбит смысла не увидел, т.к. они могут быть астрономически большими.

Переключатель «Математическая координатная сетка» показывает родную для математиков систему координат с центром координат посередине и осью Y, направленной вверх. Если режим выключен, демонстрируется координатная сетка, привычная для программистов — начало координат в левом верхнем углу и ось Y направлена вниз.

Переключатель «Анимация» включает плавное изменение угла с целью медитативного эффекта познания сущего.

Вращать вокруг центра прямоугольника

Все координаты находятся в отрицательном секторе!
При отключенном режиме математической сетки данные могут быть не видны!

Чтобы их увидеть включите режим математической сетки и сдвиньте точку вращения в положительный сектор, который находится в правом верхнем квадранте.

Get a better browser, bro…

Математическая координатная сетка

Немного кода

Delphi

// Посчитать координаты точки повернутой на Angle радиан

function CalcAnglePoint(const ACenter, APoint: TPointF;

const Angle: Single): TPointF;

var

sn,cs: single;

begin

SinCos(Angle, sn, cs);

Result.X := (APoint.X—ACenter.X) * cs —

(APoint.Y—ACenter.Y) * sn + ACenter.X;

Result.Y := (APoint.X—ACenter.X) * sn +

(APoint.Y—ACenter.Y) * cs + ACenter.Y;

end;

JavaScript

// расчет координат вершин по углу и центру вращения

// angle — угол в радианах

// center — точка, вокруг которой происходит вращение

// points — массив с координатами вершин прямоугольника

// vpoints — массив с повернутыми координатами вершин

// массивы points и vpoints должны быть одной размерности

ssin = Math.sin(angle);

scos = Math.cos(angle);

for (let i = 0; i < points.length; i++) {

vpoints[i].x = center.x + (points[i].x — center.x) * scos —

(points[i].y — center.y) * ssin;

vpoints[i].y = center.y + (points[i].x — center.x) * ssin +

(points[i].y — center.y) * scos;

}

Вращение прямоугольника вокруг произвольной точки и нахождение координат вершин производится таким незамысловатым кодом. Стоит отметить, что функции применимы к любому количеству вершин. Таким образом можно посчитать координаты любого многоугольника.

Друзья, спасибо за внимание!

Подписывайтесь на телегу.

Пишите комментарии.

Спрашивайте.

Поискать похожие темы на сайте.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Движения
Поворот

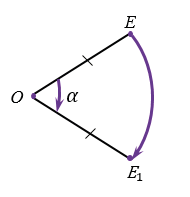
Пусть О — точка на плоскости, 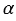— угол поворота.

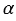
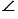
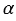
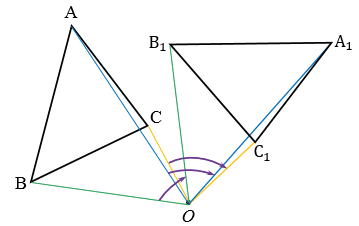
Поворот плоскости вокруг точки О на угол — это отображение плоскости на себя, при котором каждая точка Е отображается в такую точку Е₁, что ОЕ = ОЕ₁ и ЕОЕ₁ = .

При повороте плоскости вокруг точки О сама точка О остается на месте, т.е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке (как на рисунке выше) или против часовой стрелки.

Доказательство

Дано: О — центр поворота, 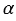— угол поворота по часовой стрелке (случай поворота против часовой стрелки рассматривается аналогично), точки Е и К отображаются при повороте в точки Е₁ и К₁.

Доказать: поворот — движение.

Доказательство:

1 случай

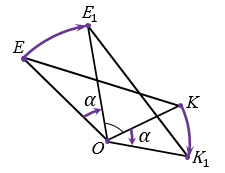
Точки О, Е и К не лежат на одной прямой.

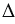
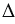
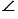
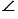
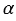
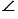
ОЕК = ОЕ₁К₁ по двум сторонам и углу между ними (ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, ЕОК = Е₁ОК₁ = + Е₁ОК). В равных треугольниках элементы соответственно равны поэтому ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

2 случай

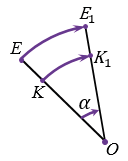
Точки О, Е и К лежат на одной прямой.

ЕК = ОЕ — ОК и Е₁К₁ = ОЕ₁ — ОК₁, при этом ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, следовательно, ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

Пример

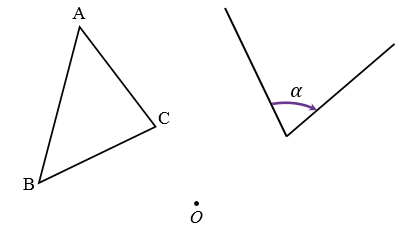
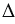
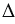
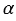
Построить А₁В₁С₁, который получается из АВС поворотом вокруг точки О по часовой стрелке на угол .

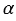
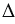
Построим точки А₁, В₁ и С₁, которые получаются из точек А, В и С поворотом вокруг точки О по часовой стрелке на угол . Соединяя попарно точки А₁, В₁, С₁ отрезками, получим искомый А₁В₁С₁.

Советуем посмотреть:

Отображение плоскости на себя

Понятие движения

Наложения и движения

Параллельный перенос

Движения

Правило встречается в следующих упражнениях:

7 класс

Задание 1166,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1167,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1168,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1169,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1170,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1171,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1183,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1303,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Лучший ответ

Ответы

Теория

Интерактив

Немного кода

Delphi

JavaScript

Доказательство

Пример

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Не пропустите также: