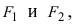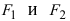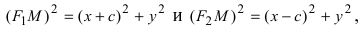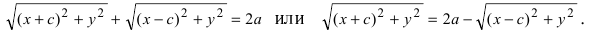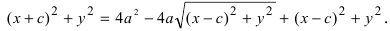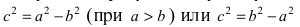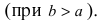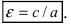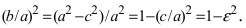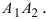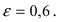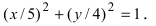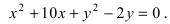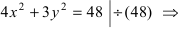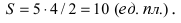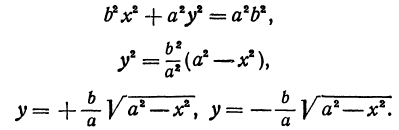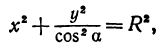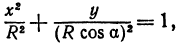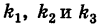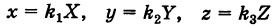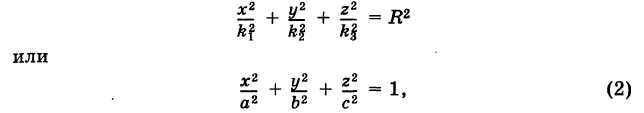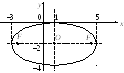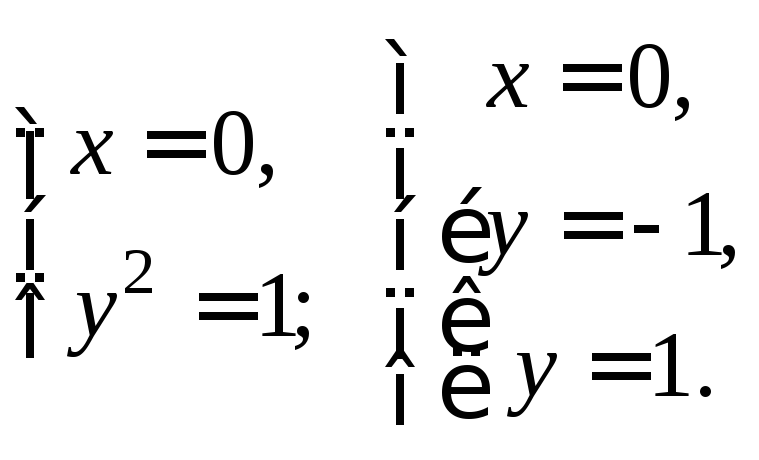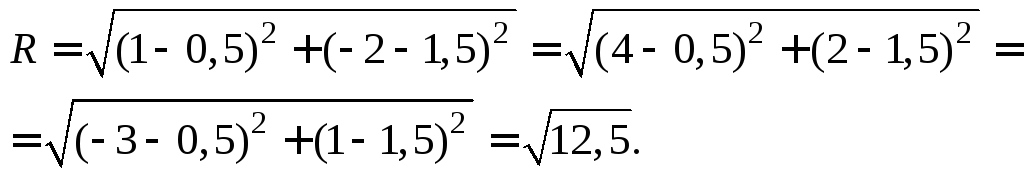Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 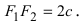
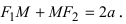
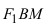
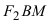
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 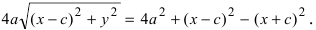
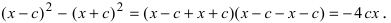
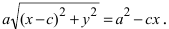
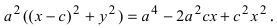
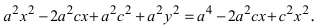
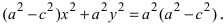
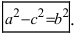
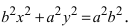
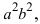
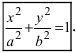
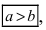
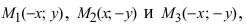
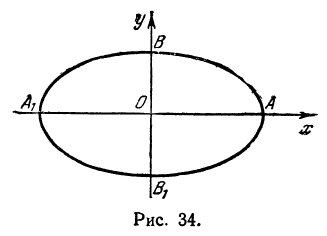
Определение: Найденные точки называются вершинами эллипса.
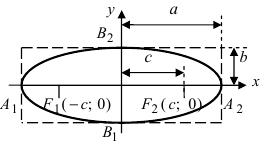
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 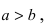
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 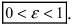
Если 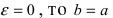
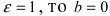
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 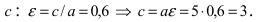
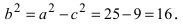
Пример:
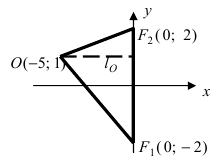
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 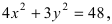
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
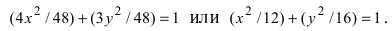
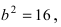
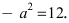
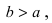
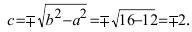
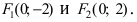
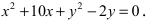
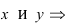
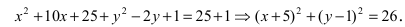
Построим в декартовой системе координат треугольник 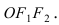
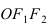
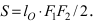
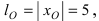
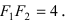
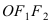
Эллипс в высшей математике
где 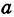
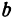
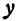
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
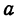

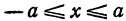
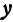
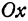
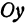
При 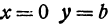
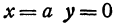
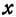

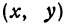
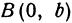
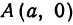
Полученная линия называется эллипсом. Число 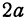
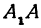
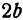
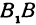
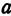
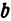
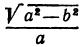
Пример:
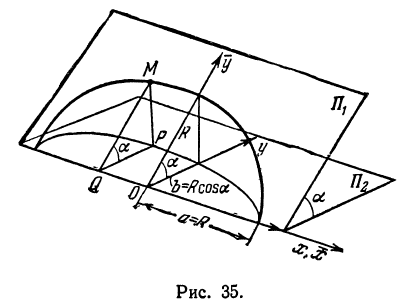
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 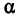
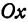
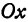
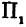
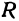
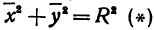
Пусть точка 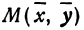
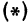
Обозначим проекцию точки 
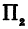
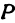
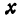
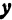


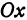
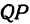
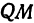
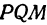
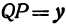
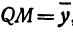
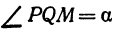
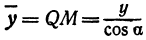


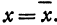
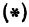
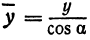
а это есть уравнение эллипса с полуосями 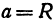
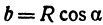
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 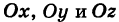
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 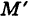
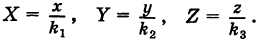
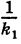
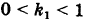
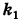
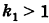
Подставляя эти формулы в уравнение (1), будем иметь
где 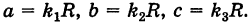
Величины 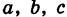
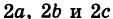
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
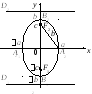
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. ( Директориальное свойство эллипса)
Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Приведем уравнение эллипса к каноническому виду:
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<5^2-3^2>=sqrt<16>=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac<4><5>;$ г) $D_1: x=-frac<25><4>$ и $D_2: x=frac<25><4>.$
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><2/3>=-frac<9> <2>$ и $D_2: x=frac<3><2/3>=frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$
Таким образом, уравнение эллипса $frac<16>+frac<4>=1.$
Далее найдем координаты фокусов:
$c=sqrt=sqrt<16-4>=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$
Примеры.
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Приведем уравнение гиперболы к каноническому виду:
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<3^2+4^2>=sqrt<25>=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
г) Асимптоты гиперболы находим по формулам $y=pmfracx:$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac<5><3>;$ г) $y=pmfrac<4><3>x;$ д ) $D_1: x=-frac<9><5>$ и $D_2: x=frac<9><5>.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$
$$y+3=frac<4><3>(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac<4><3>(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><5/3>=-frac<9> <5>$ и $D_2: x=frac<3><5/3>=frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrtRightarrow c=sqrt<16+9>=sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<4><5/4>Rightarrow x=-frac<16><5>Rightarrow 5x+16=0;$
$D_2: x=frac<4><5/4>Rightarrow x=frac<16><5>Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
Ответ: $r_1=9/4,$ $r_2=frac<41><4>;$ $d_1=frac<41><5>;$ $d_2=frac<9><5>.$
2.273. Найти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt<9+16>=sqrt <25>=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
Чтобы н айти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
Решим уравнение $5x^2+18x-72=0:$
Находим соответствующие координаты $y:$ $y_1=pmsqrt<24-2,4^2-10cdot 2,4>=sqrt<-5,76>$ — нет корней .
Ответ: $(-6, pm4sqrt 3).$
Парабола.
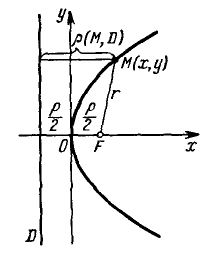
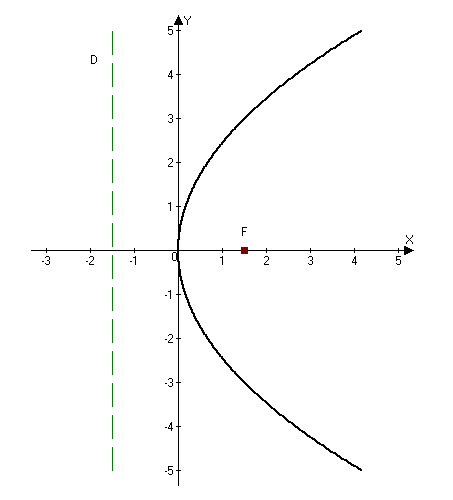
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac
<2>, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Ответ: $p=3.$
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
Ответ: $6.$
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac<3><4>.$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac<3><4>cdot 3+bRightarrow b=-frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=frac<3><4>x-frac<9><4>.$
Далее, найдем точку пересечения найденной прямой с параболой:
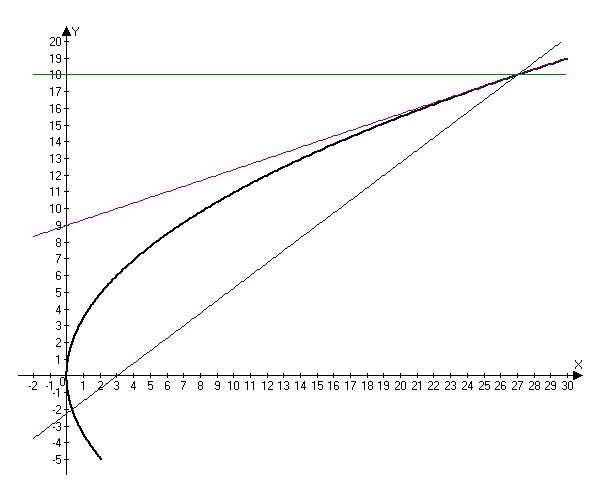
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac<18^2><12>=frac<324><12>=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac<1><3>(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac<3><4>x-frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac<1+k_1cdot k_2>$
$$L_2: x-3y+27=0Rightarrow y=frac<1><3>x+9Rightarrow k_2=frac<1><3>.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac<1><3>$ и $tgalpha=k_1=frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg(2beta-alpha)=frac<1+tg2beta tgalpha>=frac<frac<3><4>-frac<3><4>><1+frac<3><4>frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
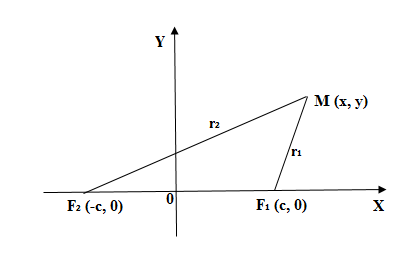
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
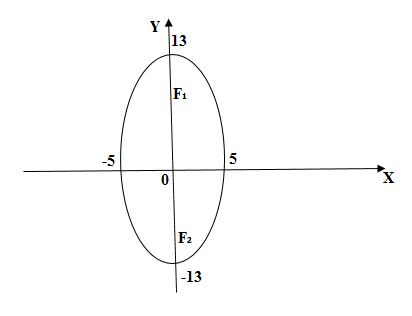
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
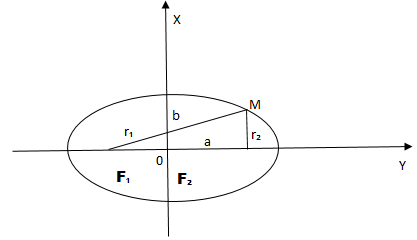
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
http://mathportal.net/index.php/component/content/article/87-visshaya-matematika/analiticheskaya-geometriya/154-ellips-giperbola-parabola-direktorialnoe-svojstvo-ellipsa-i-giperboly-polyarnyj-parametr
http://function-x.ru/curves_ellipse.html
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
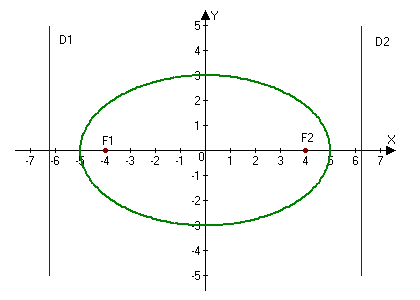
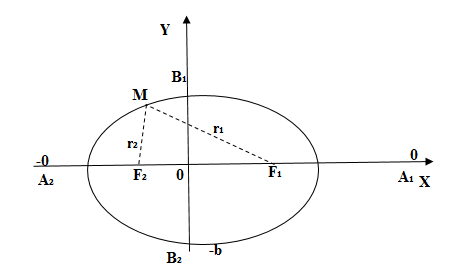
Эллипс с каноническим уравнением $frac{x^2}{a^2}+frac{y^2}{b^2}=1, ageq b>0,$ имеет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2-b^2}geq 0,$ называются фокусами эллипса векторы $overline{F_1M}$ и $overline{F_2M} -$ фокальными радиус-векторами, а числа $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac{x^2}{a^2}+frac{y^2}{a^2}=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Число $e=frac{c}{a}=sqrt{1-frac{b^2}{a^2}} ,, (0leq e<1)$ называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при $e=0$ эллипс является окружностью.)
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. (Директориальное свойство эллипса)
Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Решение.
Приведем уравнение эллипса к каноническому виду:
$$ 9x^2+25y^2=225 |:225Rightarrowfrac{9x^2}{225}+frac{25y^2}{225}=1Rightarrow$$
$$Rightarrowfrac{x^2}{25}+frac{y^2}{9}=1Rightarrowfrac{x^2}{5^2}+frac{y^2}{3^2}=1.$$
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2-b^2}:$
$c=sqrt{5^2-3^2}=sqrt{16}=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
в) Эксцентриситет $e=frac{c}{a}=frac{4}{5}.$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{5}{4/5}=-frac{25}{4}$ и $D_2: x=frac{5}{4/5}=frac{25}{4}.$
Сделаем рисунок:
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac{4}{5};$ г) $D_1: x=-frac{25}{4}$ и $D_2: x=frac{25}{4}.$
{jumi[*3]}
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Решение.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
$$5x^2+9y^2-30x+18y+9=(5x^2-30x)+(9y^2+18y)+9=$$
$$5(x^2+6x+9-9)+9(y^2+2y+1-1)+9=5(x+3)^2-45+9(y+1)^2-9+9=$$
$$5(x+3)^2+9(y+1)^2-45=0Rightarrow5(x+3)^2+9(y+1)^2=45|:45Rightarrow$$
$$ frac{(x+3)^2}{9}+frac{(y+1)^2}{5}=1Rightarrowfrac{(x+3)^2}{3^2}+frac{(y+1)^2}{(sqrt 5)^2}=1.$$
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
$c=sqrt{a^2-b^2}Rightarrow c=sqrt{9-5}=sqrt 4=2Rightarrow e=frac{c}{a}=frac{2}{3}.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{2/3}=-frac{9}{2} $ и $D_2: x=frac{3}{2/3}=frac{9}{2}.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
$$D_1: x=3-frac{9}{2}=frac{6-9}{2}=-frac{3}{2}Rightarrow 2x+3=0 $$ $$D_2: x=3+frac{9}{2}=frac{6+9}{2}=frac{15}{2}Rightarrow2x-15=0.$$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac{2}{3}.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac{x^2}{a^2}+frac{y^2}{b^2}=1:$
$$frac{2^2}{a^2}+frac{(sqrt 3)^2}{2^2}=1Rightarrow frac{4}{a^2}+frac{3}{4}=1Rightarrow frac{4}{a^2}=frac{1}{4}Rightarrow a^2=16Rightarrow a=4.$$
Таким образом, уравнение эллипса $frac{x^2}{16}+frac{y^2}{4}=1.$
Далее найдем координаты фокусов:
$c=sqrt{a^2-b^2}=sqrt{16-4}=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline {F_1M_1}=(2+2sqrt 3, sqrt 3),$ $overline{F_2M_1}=(2-2sqrt 3, sqrt 3).$
Соответственно, $r_1=|overline {F_1M_1}|=sqrt{(2+2sqrt 3)^2+ (sqrt 3)^2}=sqrt{4+8sqrt 3+12+3}=$ $=sqrt{16+8sqrt 3+3}=sqrt{(4+sqrt 3)^2}=4+sqrt 3,$
$r_2=|overline {F_2M_1}|=sqrt{(2-2sqrt 3)^2+ (sqrt 3)^2}=sqrt{4-8sqrt 3+12+3}=$ $=sqrt{16-8sqrt 3+3}=sqrt{(4-sqrt 3)^2}=4-sqrt 3.$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$e=frac{c}{a}=frac{2sqrt 3}{4}=frac{sqrt 3}{2};$
$D_1: x=-frac{4}{frac{sqrt 3}{2}}=-frac{8}{sqrt 3}Rightarrow sqrt 3 x+8=0;$
$D_2: x=frac{4}{frac{sqrt 3}{2}}=frac{8}{sqrt 3}Rightarrow sqrt 3 x-8=0.$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
$$d_1=left|frac{2sqrt 3+8}{sqrt{(sqrt 3)^2}}right|=frac{2sqrt 3+8}{sqrt 3};$$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
$$d_2=left|frac{2sqrt 3-8}{sqrt{(sqrt 3)^2}}right|=frac{8-2sqrt 3}{sqrt 3}.$$
Ответ: $frac{x^2}{16}+frac{y^2}{4}=1,$ $r_1=4+sqrt 3,$ $r_2=4-sqrt 3,$ $d_1=frac{8+2sqrt 3}{sqrt 3},$ $d_2=frac{8-2sqrt 3}{sqrt 3}.$
Гипербола.
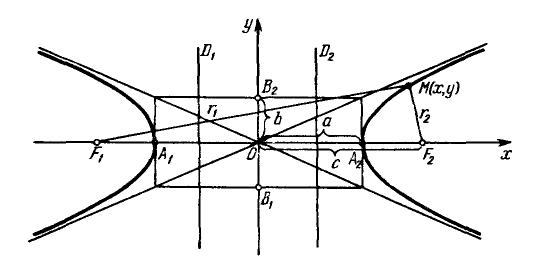
Гипербола с каноническим уравнением $frac{x^2}{a^2}-frac{y^2}{b^2}=1, a,b>0,$ имеет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Прямые $y=pmfrac{b}{a}x$ являются асимптотами гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2+b^2}geq 0,$ называются фокусами гиперболы, векторы $overline{F_1M}$ и $overline{F_2M} -$ фокальными радиус-векторами, а числа $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Число $e=frac{c}{a}=sqrt{1+frac{b^2}{a^2}} ,, (1<e<+infty)$ называется эксцентриситетом гиперболы и является мерой ее «сплюснутости». В частном случае $a=b$ гипербола называется равносторонней; ее эксцентриситет равен $e=sqrt{2},$ а угол между асимптотами равен $pi/2.$
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
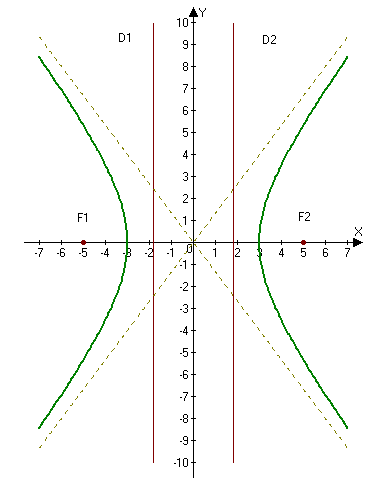
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Решение.
Приведем уравнение гиперболы к каноническому виду:
$$ 16x^2-9y^2=144 |:144Rightarrowfrac{16x^2}{144}-frac{9y^2}{144}=1Rightarrow$$
$$Rightarrowfrac{x^2}{9}-frac{y^2}{16}=1Rightarrowfrac{x^2}{3^2}+frac{y^2}{4^2}=1.$$
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt{a^2+b^2}:$
$c=sqrt{3^2+4^2}=sqrt{25}=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
в) Эксцентриситет $e=frac{c}{a}=frac{5}{3}.$
г) Асимптоты гиперболы находим по формулам $y=pmfrac{b}{a}x:$
$$y=pmfrac{4}{3}x.$$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{5/3}=-frac{9}{5}$ и $D_2: x=frac{3}{5/3}=frac{9}{5}.$
Сделаем рисунок:
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac{5}{3};$ г) $y=pmfrac{4}{3}x;$ д) $D_1: x=-frac{9}{5}$ и $D_2: x=frac{9}{5}.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Решение.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
$$16x^2-9y^2-64x-54y-161=(16x^2-64x)-(9y^2+54y)-161=$$
$$16(x^2-4x+4-4)-9(y^2+6y+9-9)-161=16(x-2)^2-64-9(y+3)^2+81-161=$$
$$16(x-2)^2-9(y+3)^2-144=0Rightarrow16(x-2)^2-9(y+3)^2=144|:144Rightarrow$$
$$ frac{(x-2)^2}{9}-frac{(y+3)^2}{16}=1Rightarrowfrac{(x-2)^2}{9}-frac{(y+3)^2}{16}=1.$$
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
$c=sqrt{a^2+b^2}Rightarrow c=sqrt{9+16}=sqrt {25}=5Rightarrow e=frac{c}{a}=frac{5}{3}.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfrac{b}{a}x,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac{b}{a}(x-x_0),$
$$y+3=frac{4}{3}(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac{4}{3}(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac{3}{5/3}=-frac{9}{5} $ и $D_2: x=frac{3}{5/3}=frac{9}{5}.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
$$D_1: x=2-frac{9}{5}=frac{10-9}{5}=frac{1}{5}Rightarrow 5x-1=0 $$
$$D_2: x=2+frac{9}{5}=frac{10+9}{5}=frac{19}{5}Rightarrow 5x-19=0 $$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac{5}{3},$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac{x^2}{16}-frac{y^2}{9}=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
$$frac{x^2}{16}-frac{y^2}{9}=1Rightarrow frac{(-5)^2}{16}-frac{(9/4)^2}{9}=frac{25}{16}-frac{81}{16cdot 9}=frac{25cdot 9-81}{144}=frac{144}{144}=1.$$
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac{x^2}{16}-frac{y^2}{9}=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrt{a^2+b^2}Rightarrow c=sqrt{16+9}=sqrt {25}=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline{F_1M}|$ и $r_2=|overline{F_2M}|.$
$$overline{F_1M}=(-5-(-5), 9/4)=(0, 9/4)Rightarrow |overline{F_1M}=sqrt{(9/4)^2}|=9/4.$$
$$overline{F_2M}=(-5-5, 9/4)=(-10, 9/4)Rightarrow |overline{F_1M}=sqrt{10^2+(9/4)^2}|=$$ $$=sqrt{100+81/16}=sqrtfrac{1681}{16}=frac{41}{4}.$$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$e=frac{c}{a}=frac{5}{4};$
$D_1: x=-frac{4}{5/4}Rightarrow x=-frac{16}{5}Rightarrow 5x+16=0;$
$D_2: x=frac{4}{5/4}Rightarrow x=frac{16}{5}Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
$$d_1=left|frac{5cdot 5+16}{sqrt{5^2}}right|=frac{41}{5};$$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
$$d_2=left|frac{5cdot 5-16}{sqrt{5^2}}right|=frac{9}{5}.$$
Ответ: $r_1=9/4,$ $r_2=frac{41}{4};$ $d_1=frac{41}{5};$ $d_2=frac{9}{5}.$
2.273. Найти точки гиперболы $frac{x^2}{9}-frac{y^2}{16}=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrt{a^2+b^2}Rightarrow c=sqrt{9+16}=sqrt {25}=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
$$(x+5)^2+y^2=7^2.$$
Чтобы найти точки гиперболы $frac{x^2}{9}-frac{y^2}{16}=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
$$left{begin{array}{lcl}frac{x^2}{9}-frac{y^2}{16}=1\(x+5)^2+y^2=7^2end{array}right.$$
$$Rightarrowleft{begin{array}{lcl}frac{x^2}{9}-frac{y^2}{16}=1\y^2=7^2-(x+5)^2end{array}right.Rightarrowleft{begin{array}{lcl}frac{x^2}{9}-frac{7^2-(x+5)^2}{16}=1\y^2=7^2-(x+5)^2end{array}right.$$
$$Rightarrowleft{begin{array}{lcl}16x^2-9(49-x^2-10x-25)=144\y^2=7^2-(x+5)^2end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}16x^2-216+9x^2+90x=144\y^2=7^2-(x+5)^2end{array}right.Rightarrow$$
$$Rightarrowleft{begin{array}{lcl}25x^2+90x-360=0\y^2=7^2-(x+5)^2end{array}right.Rightarrowleft{begin{array}{lcl}5x^2+18x-72=0\y^2=7^2-(x+5)^2end{array}right.$$
Решим уравнение $5x^2+18x-72=0:$
$D=18^2+4cdot5cdot72=324+1440=1764=42^2.$
$x_1=frac{-18+42}{10}=frac{24}{10}=2,4;$ $x_2=frac{-18-42}{10}=-6.$
Находим соответствующие координаты $y:$ $y_1=pmsqrt{24-2,4^2-10cdot 2,4}=sqrt{-5,76}$ — нет корней.
$y_2=pmsqrt{24-6^2+10cdot5}=pm4sqrt{3}.$
Ответ: $(-6, pm4sqrt 3).$
Парабола.
Парабола с каноническим уравнением $y^2=2px, p>0,$ имеет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac{p}{2}, 0right)$ называется фокусом параболы, вектор $overline{FM} -$ фокальным радиус-векторам, а число $r=|overline{FM}| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Сделаем рисунок:
Ответ: $p=3.$
{jumi[*4]}
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
$$y^2=-2cdotfrac{1}{2}x=-x.$$
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
$y^2=4(x-2).$
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
$r=|FM|=sqrt{(3-3)^2+(6-0)^2}=6.$
Ответ: $6.$
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac{3}{4}.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac{3}{4}$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac{3}{4}.$
$y=frac{3}{4}x+b$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac{3}{4}cdot 3+bRightarrow b=-frac{9}{4}.$ Таким образом, уравнение луча, направленного из фокуса $y=frac{3}{4}x-frac{9}{4}.$
Далее, найдем точку пересечения найденной прямой с параболой:
$$left{begin{array}{lcl}y=frac{3}{4}x-frac{9}{4}\y^2=12xend{array}right.Rightarrowleft{begin{array}{lcl}3x-4y-9=0\x=frac{y^2}{12}end{array}right.Rightarrowleft{begin{array}{lcl}frac{3y^2}{12}-4y-9=0\x=frac{y^2}{12}end{array}right.Rightarrow$$ $$left{begin{array}{lcl}y^2-16y-36=0\x=frac{y^2}{12}end{array}right.$$
$$y^2-16y-36=0$$
$$D=256+4cdot1cdot36=256+144=400.$$
$$y_1=frac{16+20}{2}=18qquad y_2=frac{16-20}{2}=-2.$$
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac{18^2}{12}=frac{324}{12}=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
$$y=sqrt{12x}Rightarrow y’=sqrt {12}frac{1}{2sqrt x}=frac{sqrt 3}{sqrt{x}}Rightarrow$$
$$Rightarrow y'(27)=frac{sqrt 3}{sqrt{ 27}}=frac{1}{3}.$$
$$y(27)=18.$$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac{1}{3}(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac{3}{4}x-frac{9}{4}$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac{k_1-k_2}{1+k_1cdot k_2}$
$$L_1: y=frac{3}{4}x-frac{9}{4}Rightarrow k_1=frac{3}{4};$$
$$L_2: x-3y+27=0Rightarrow y=frac{1}{3}x+9Rightarrow k_2=frac{1}{3}.$$
$$tg beta=tg(L_1, L_2)=frac{frac{3}{4}-frac{1}{3}}{1+frac{3}{4}frac{1}{3}}=frac{frac{5}{12}}{frac{5}{4}}=frac{1}{3}.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac{1}{3}$ и $tgalpha=k_1=frac{3}{4}$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg 2beta=frac{2tgbeta}{1-tg^2beta}=frac{frac{2}{3}}{1-frac{1}{9}}=frac{frac{2}{3}}{frac{8}{9}}=frac{3}{4}.$$
$$tg(2beta-alpha)=frac{tg2beta-tgalpha}{1+tg2beta tgalpha}=frac{frac{3}{4}-frac{3}{4}}{1+frac{3}{4}frac{3}{4}}=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
Ответ: $y=18.$
Эллипсом
называется геометрическое место точек
плоскости, координаты которых удовлетворяют
уравнению
(9.7)
где
(9.8)
Уравнение (9.7)
называется
каноническим
уравнением эллипса.
Параметры эллипса
Точки F1(–c,
0) и F2(c,
0), где
называютсяфокусами
эллипса,
при этом величина 2c
определяет междуфокусное
расстояние.
Точки А1(–а,
0), А2(а,
0), В1(0,
–b),
B2(0,
b)
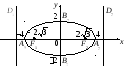
называются вершинами
эллипса
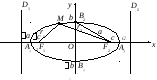
(рис. 9.2), при этом А1А2
= 2а
образует большую ось эллипса, а В1В2
– малую,
– центр эллипса.
Основные параметры
эллипса, характеризующие его форму:
ε
= с/a
– эксцентриситет
эллипса;
–фокальные
радиусы эллипса
(точка М
принадлежит эллипсу), причем r1
= a
+ εx,
r2
= a
– εx;
–директрисы
эллипса.
Рис. 9.2
Для эллипса
справедливо:
директрисы не пересекают границу и
внутреннюю область эллипса, а также
обладают свойством
Эксцентриситет
эллипса выражает его меру «сжатости».
Если b
> a
> 0, то
эллипс задается уравнением (9.7), для
которого вместо условия (9.8) выполняется
условие
.
(9.9)
Тогда 2а
– малая ось, 2b
– большая ось,
– фокусы (рис. 9.3). При этомr1
+ r2
= 2b,
ε
= c/b,
директрисы определяются уравнениями:
Рис. 9.3
При
условии
имеем (в виде частного случая эллипса)окружность
радиуса R
= a.
При этом с
= 0, а значит, ε = 0.
Точки эллипса
обладают характеристическим
свойством:
сумма расстояний от каждой из них до
фокусов есть величина постоянная, равная
2а
(рис. 9.2).
Для параметрического
задания эллипса
(формула (9.7)) в случаях выполнения условий
(9.8) и (9.9) в качестве параметра t
может быть взята величина угла между
радиус-вектором точки, лежащей на
эллипсе, и положительным направлением
оси Ox:
где
Если центр эллипса
с полуосями
находится в точке
то его уравнение имеет вид:
(9.10)
Пример 1.
Привести уравнение эллипса x2
+ 4y2
= 16 к каноническому виду и определить
его параметры. Изобразить эллипс.
Решение.
Разделим уравнение x2 + 4y2 = 16
на 16, после чего получим:
По виду полученного
уравнения заключаем, что это каноническое
уравнение эллипса (формула (9.7)), где а
= 4 – большая полуось, b
= 2 – малая полуось. Значит, вершинами
эллипса являются точки A1(–4, 0),
A2(4, 0),
B1(0, –2),
B2(0, 2).
Так как
– половина междуфокусного расстояния,
то точкиявляются фокусами эллипса. Вычислим
эксцентриситет:
Директрисы D1,
D2
описываются уравнениями:
Изображаем эллипс
(рис. 9.4).
Рис. 9.4
Пример 2.
Определить параметры эллипса
Решение.
Сравним данное уравнение с каноническим
уравнением эллипса
со смещенным центром. Находим центр
эллипсаС:
Большая полуось
малая полуось
прямые
– главные оси. Половина междуфокусного
расстоянияа значит, фокусы
Эксцентриситет
ДиректрисыD1
и D2
могут быть описаны с помощью уравнений:
(рис. 9.5).
Рис. 9.5
Пример 3.
Определить, какая кривая задается
уравнением, изобразить ее:
1) x2
+ y2
+ 4x
– 2y
+ 4 = 0; 2) x2
+ y2
+ 4x
– 2y
+ 6 = 0;
3) x2
+ 4y2
– 2x
+ 16y
+ 1 = 0; 4) x2
+ 4y2
– 2x
+ 16y
+ 17 = 0;
5)
Решение.
1) Приведем уравнение к каноническому
виду методом выделения полного квадрата
двучлена:
x2
+ y2
+ 4x
– 2y
+ 4 = 0;
(x2
+ 4x)
+ (y2
– 2y)
+ 4 = 0;
(x2
+ 4x
+ 4) – 4 + (y2
– 2y
+ 1) – 1 + 4 = 0;
(x
+ 2)2
+ (y
– 1)2
= 1.
Таким образом,
уравнение может быть приведено к виду
(x
+ 2)2
+ (y
– 1)2
= 1.
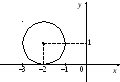
Это уравнение
окружности с центром в точке (–2, 1) и
радиусом R = 1
(рис. 9.6).
Рис. 9.6
2)
Выделяем полные квадраты двучленов в
левой части уравнения и получаем:
(x
+ 2)2
+ (y
– 1)2
= –1.
Это уравнение не
имеет смысла на множестве действительных
чисел, так как левая часть неотрицательна
при любых действительных значениях
переменных x
и y,
а правая – отрицательна. Поэтому говорят,
что это уравнение «мнимой окружности»
или оно задает пустое множество точек
плоскости.
3) Выделяем полные
квадраты:
x2
+ 4y2
– 2x
+ 16y
+ 1 = 0;
(x2
– 2x
+ 1) – 1 + 4(y2
+ 4y
+ 4) – 16 + 1 = 0;
(x
– 1)2
+ 4(y
+ 2)2
– 16 = 0;
(x
– 1)2
+ 4(y
+ 2)2
= 16.
Значит, уравнение
имеет вид:
или
Полученное
уравнение, а следовательно, и исходное
задают эллипс. Центр эллипса находится
в точке О1(1,
–2), главные оси задаются уравнениями
y
= –2, x
= 1, причем большая полуось а
= 4, малая полуось b
= 2 (рис. 9.7).
Рис. 9.7
4) После выделения
полных квадратов имеем:
(x
– 1)2
+ 4(y
+ 2)2
– 17 + 17 = 0 или (x
– 1)2
+ 4(y
+ 2)2
= 0.
Полученное уравнение
задает единственную точку плоскости с
координатами (1, –2).
5) Приведем уравнение
к каноническому виду:
Очевидно, оно
задает эллипс, центр которого находится
в точке
главные оси задаются уравнениями
причем большая полуось
малая полуось
(рис. 9.8).
Рис. 9.8
Пример 4.
Записать уравнение касательной к
окружности радиуса 2 с центром в
правом фокусе эллипса x2
+ 4y2
= 4 в точке пересечения с осью ординат.
Решение.
Уравнение эллипса приведем к каноническому
виду (9.7):
Значит,
и правый фокус –
Поэтому, искомое уравнение окружности
радиуса 2 имеет вид (рис. 9.9):
Окружность
пересекает ось ординат в точках,
координаты которых определяются из
системы уравнений:
Получаем:
Пусть это точки N
(0; –1) и М
(0; 1). Значит, можно построить две
касательные, обозначим их Т1
и Т2.
По известному свойству касательная
перпендикулярна радиусу, проведенному
в точку касания.
Пусть
Тогда
уравнение касательнойТ1
примет вид:
значит,
илиТ1:
Тогда уравнение
касательной Т2
примет вид:
значит,
илиТ2:
Рис. 9.9
Пример 5.
Записать уравнение окружности, проходящей
через точку М(1,
–2) и точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0.
Решение.
Найдем точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0, решив систему уравнений:
Выразим х
из первого уравнения системы:
x
= 7y
– 10.
Затем подставим
во второе:
(7y
– 10)2
+ y2
– 2(7y
– 10) + 4y
– 20 = 0.
Оно равносильно
уравнению
y2
– 3y
+ 2 = 0.
Используя формулы
корней квадратного уравнения, найдем
y1
= 1, y2
= 2, откуда x1
= –3, x2
= 4.
Итак, имеем три
точки, лежащие на окружности: M(1,
–2), M1(4,
2) и M2(–3,
1). Пусть О1(x0,
y0)
– центр окружности. Тогда
гдеR
– радиус окружности.
Найдем координаты
векторов:
Значит,
что равносильно
системе
Упрощаем ее:
Решая последнюю
систему, получаем ответ:
Таким образом,
центр окружности находится в точке
(0,5; 1,5), ее радиус
Тогда каноническое
уравнение искомой окружности имеет
вид:
Задания
Соседние файлы в папке Часть 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и
. Допустим, что расстояние
=
– фокусное расстояние.
Рис. 1
– фокусы .
;
,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью,
(теорема Пифагора). Если же точка
находится на пересечении его с горизонтальной осью,
. Так как по определению сумма
– постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами
тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и
на оси
симметричной к началу координат. Тогда у фокусов будут такие координаты
и
(см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через
и
– расстояние от точки
к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) ,
и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается
. Так как
, тогда
, и поэтому
.
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки
тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти
.
Если , тогда
. Если же
, тогда
. Точки
и
, а также симметричные с ними
,
– вершины эллипса, точка
– центр эллипса,
=
большая ось,
– малая ось эллипса.
Если первой четверти, тогда из
получается, что при возрастании
от
к
значение
падает от
к
. (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом
.
2. Уравнение касательной к эллипсу в точке с координатами
:
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и
у треугольника
, тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда
– получается круг. Если же
, тогда
– эллипс превращается в отрезок. В некоторых случаях
. Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и
, тогда вычислим
– полуфокусное расстояние.
Строим фокусы и
на расстоянии один от другого
Концы не растянутой нити длиной
закрепляем в точках
и
. Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках и
. (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.
Калькулятор точки на эллипсе
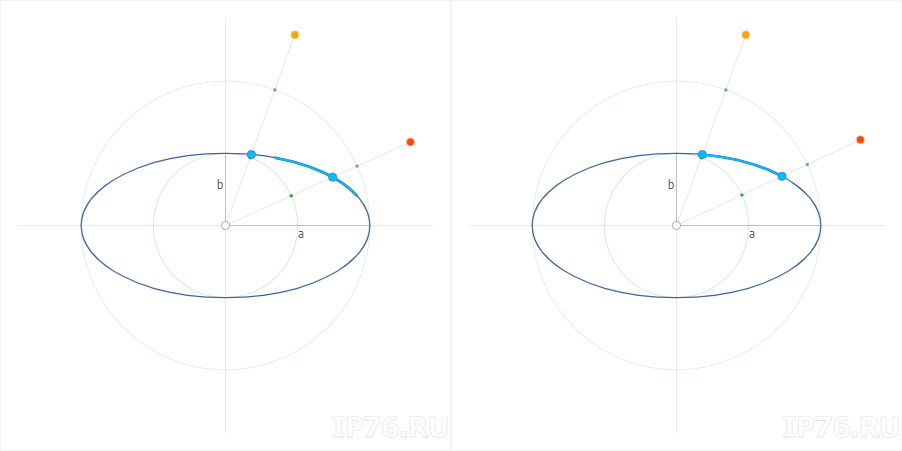
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Маркеры кликабельны и таскабельны.
Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx
Эллипс:
a:
b:
Углы (град.):
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
|
//— находим параметр (некий угол) для уравнения — SinCos(Angle,sn,cs); t := ArcTan2(a*sn, b*cs); |
Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.
О параметре
Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.
В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var t1 = start; var t2 = finish; ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.
Перепишем функцию с учетом нахождения параметра:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var sn = Math.sin(start); var cs = Math.cos(start); var t1 = Math.atan2(a*sn, b*cs); sn = Math.sin(finish); cs = Math.cos(finish); var t2 = Math.atan2(a*sn, b*cs); ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке справа видим, что все встало на свои места. Идеальная дуга )
Координаты точки наклонного эллипса
Перенесено в отдельную статью.
Практика
Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.
|
//****************************************************************** // Найти угол, который будет использован в расчете точки на элипсе // Т.е. тот самый параметр t в параметрическом уравнении эллипса: // x = a * cos t // y = b * sin t //****************************************************************** function GetEllipseAngleParam(ARect : TRectF; Angle : Extended) : Extended; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y begin a := ARect.Width/2; b := ARect.Height/2; SinCos(Angle,sn,cs); result := ArcTan2(a * sn, b * cs); end; |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//******************************************************************** // Найти координату точки на эллипсе по углу отклонения //******************************************************************** function CalcEllipsePointCoord(ARect : TRectF; Angle : extended) : TPointF; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y cnt : TPointF; // центр t : Extended; // параметр для уравнения эллипса begin // инициализация полуосей a := ARect.Width/2; b := ARect.Height/2; // центр эллипса cnt := ARect.CenterPoint; // находим параметр (некий угол) для уравнения SinCos(Angle,sn,cs); t := ArcTan2(a * sn, b * cs); // считаем результат по параметрическому уравнению SinCos (t, sn, cs); result.X := cnt.x + a * cs; result.Y := cnt.Y + b * sn; end; |
Скачать исходник + исполнямый файл
Друзья, спасибо за внимание!
Надеюсь, материал после правок стал понятней.
Подписывайтесь на телегу.
Если есть вопросы, с удовольствием отвечу )