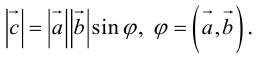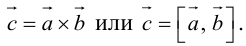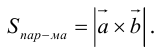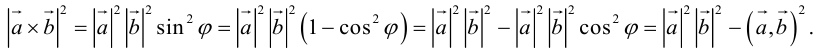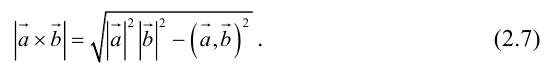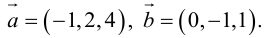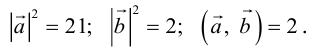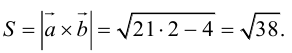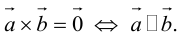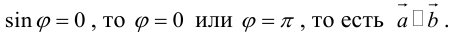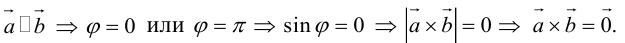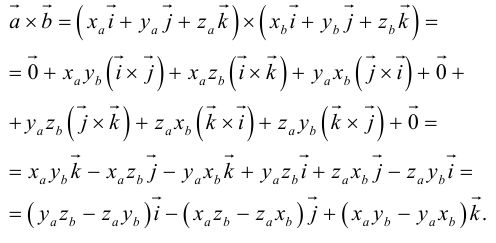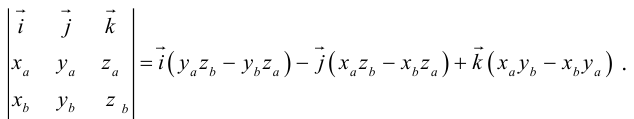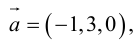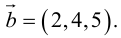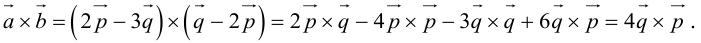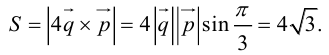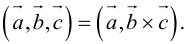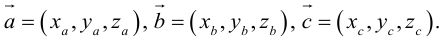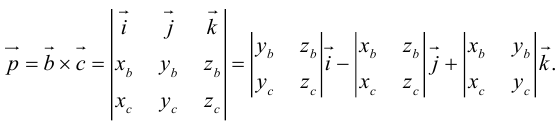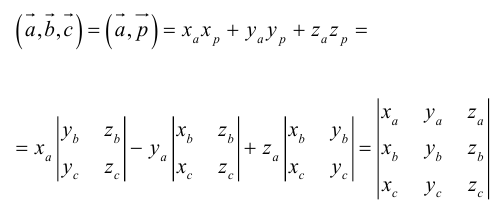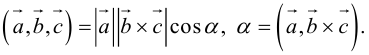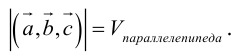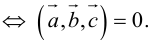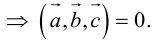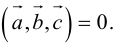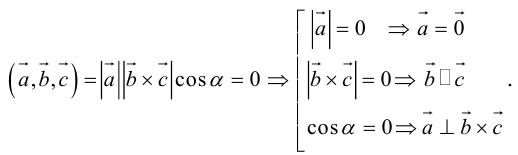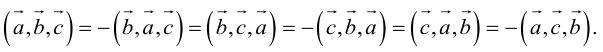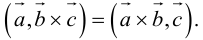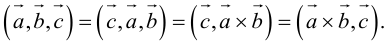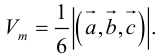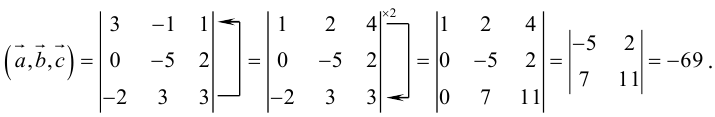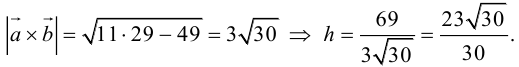Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Нахождение координат вектора
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | AB = x — Ax; By — Ay> |
| Для трехмерных задач | AB = x — Ax; By — Ay; Bz — Az> |
| Для n-мерных векторов | AB = 1 — A1; B2 — A2; . Bn — An> |
Примеры задач
Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .
Задание 2
Определим координаты точки B вектора , если координаты точки .
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = AB x + Ax = 6 + 2 = 8.
By = AB y + Ay = 14 + 5 = 19.
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx — Ax; By — Ay} |
| Для трехмерных задач | AB = {Bx — Ax; By — Ay; Bz — Az} |
| Для n-мерных векторов | AB = {B1 — A1; B2 — A2; … Bn — An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Содержание:
- Формула
- Примеры нахождения координат вектора
Формула
Чтобы найти координаты вектора $overline {A B}$, если заданы координаты его начала и конца,
необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно
координаты $Aleft(x_{A} ; y_{A}right)$ и $Bleft(x_{B} ; y_{B}right)$, то координаты вектора $overline {A B}$ вычисляются по формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)$$
Если точки заданы в пространстве и имеют координаты
$Aleft(x_{A} ; y_{A} ; z_{A}right)$ и $Bleft(x_{B} ; y_{B} ; z_{B}right)$ соответственно, то координаты вектора
$overline {A B}$ вычисляются по следующей формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)$$
Примеры нахождения координат вектора
Пример
Задание. Даны точки
$A(5 ; 1)$ и $B(4 ;-3)$. Найти координаты векторов
$overline {A B}$ и
$overline {B A}$
Решение. Точки заданны на плоскости, поэтому координаты вектора
$overline {A B}$ вычислим по формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)$$
Подставляя координаты заданных точек, получим:
$$overline{A B}=(4-5 ;-3-1)=(-1 ;-4)$$
Для нахождения вектора $overline {B A}$ исходная формула примет вид:
$$overline{B A}=left(x_{A}-x_{B} ; y_{A}-y_{B}right)$$
то есть
$$overline{B A}=(5-4 ; 1-(-3))=(1 ; 4)$$
Ответ. $overline{A B}=(-1 ;-4), overline{B A}=(1 ; 4)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки
$A(4 ; 3 ; 2)$, $B(-3 ; 2 ;-1)$ и $C(-1 ; 0 ; 1)$ . Найти координаты вектора
$overline {A B}$,
$overline {C B}$ .
Решение. Точки заданны в пространстве, поэтому для нахождения координат искомых векторов будем пользоваться формулой
$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)$
Подставляя заданные координаты, получим:
$$overline{A B}=(-3-4 ; 2-3 ;-1-2)=(-7 ;-1 ;-3)$$
Для вектора $overline {C B}$ имеем:
$overline{C B}=left(x_{B}-x_{C} ; y_{B}-y_{C} ; z_{B}-z_{C}right)$
$overline{C B}=(-3-(-1) ; 2-0 ;-1-1)=(-2 ; 2 ;-2)$
Ответ. $overline{A B}=(-7 ;-1 ;-3), overline{C B}=(-2 ; 2 ;-2)$
Читать дальше: как найти направляющие косинусы вектора.
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
«Координаты точки и координаты вектора. Как найти координаты вектора» 👇
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ — единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$
Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$
$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$
Следовательно
$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а
$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$
Значит
$koverline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.
Решение.
$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
Векторная алгебра
Векторная алгебра — это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая — конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор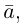
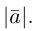
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 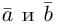
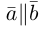
Аналогично, векторы а и b называются ортогональными (обозначение 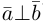
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
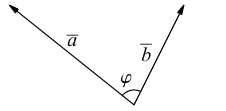
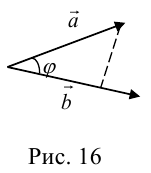
Углом между векторами 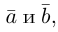
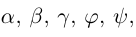
Два ненулевых вектора 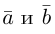
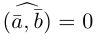
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 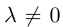
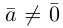
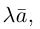
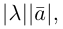
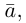
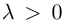
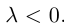
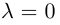
В частности, вектор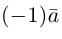
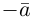
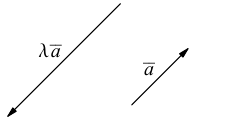
Если 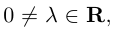
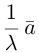
Из приведенного определения сразу же следует, что коллинеарные векторы 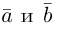
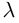
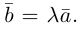
взять число 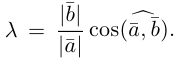
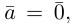
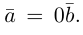
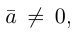
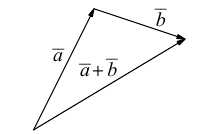
b) Сложение векторов.
Суммой двух векторов 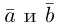
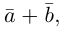
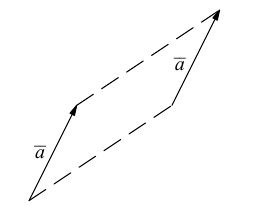
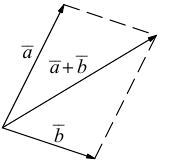
или по равносильному ему правилу параллелограмма
Вектор 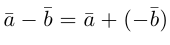
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 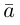
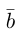
Геометрически очевидны следующие свойства проекции:
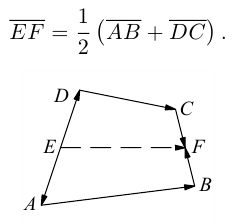
Пример №1
Пусть Е и F — середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 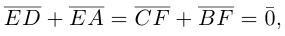
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 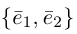
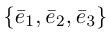
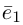
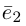
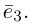
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 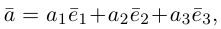
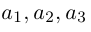
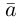
Приведем геометрическое доказательство этого утверждения.
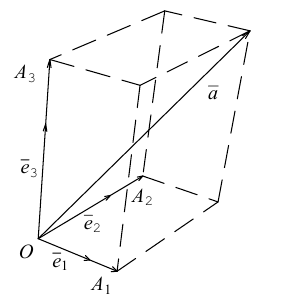
Вектор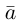
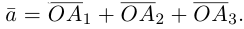
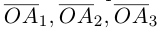
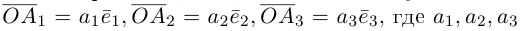
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 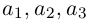
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 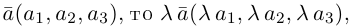
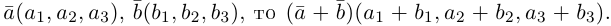
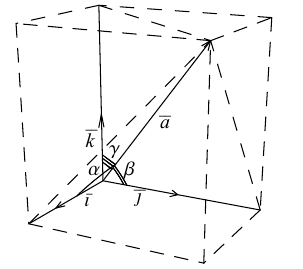
Рассмотрим теперь ортонормированный базис 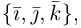
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 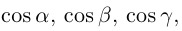
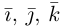
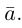
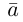
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 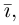
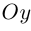
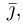
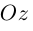
В выбранной системе координат координаты радиуса-вектора 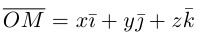
Если известны координаты начальной 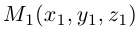
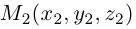
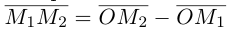
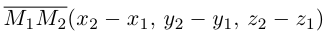
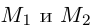
Найдем теперь координаты точки М, делящей отрезок с концами в точках 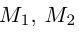
отношении 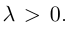
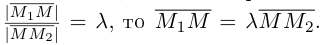
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
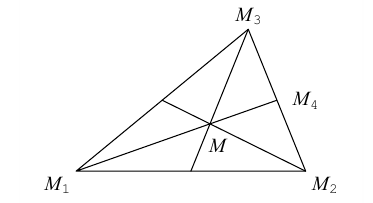
Пример №2
Треугольник задан координатами своих вершин 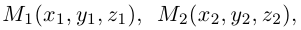
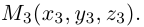
Пусть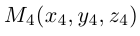
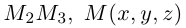
По известному свойству точки пересечения медиан 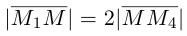
Подставив сюда найденные координаты точки 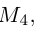
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 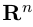
обладающая тем свойством, что любой вектор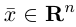
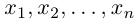
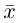
В качестве базиса в 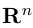
так как, очевидно, любой вектор 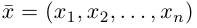
Скалярное произведение векторов
Определение: Скалярным произведением векторов 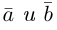
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое — из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 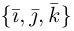
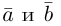
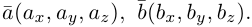
перемножим векторы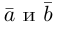
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
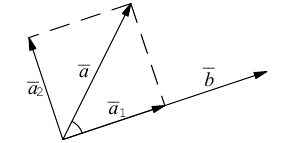
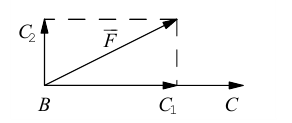
Пример №3
Разложить вектор 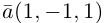
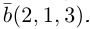
Решение.
Из чертежа следует, что 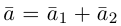
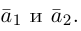
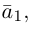
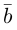
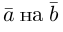
Тогда вторая ортогональная составляющая вектора 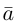
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 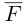
Найдем работу этой силы. Для этого разложим вектор силы 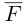
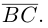
Составляющая 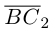
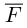
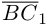
Окончательно, работа силы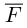
Замечание. Скалярным произведением векторов 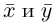
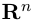
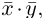
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 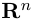
Длиной вектора 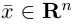
Векторы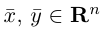
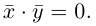
составляют ортонормированный базис пространства 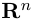
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 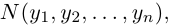
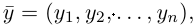
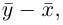
Таким образом переопределенное пространство 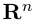
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R». Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
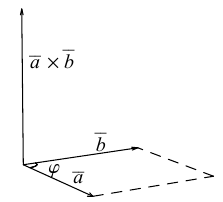
Определение: Векторным произведением некоялинеарных векторов 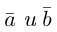

Из этого определения следует, что площадь параллелограмма, построенного на векторах 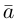
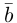

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 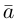
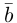
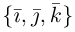
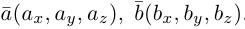
раскроем скобки в векторном произведении 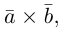
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
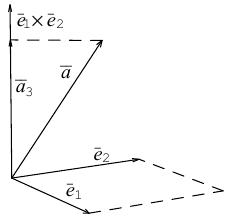
Пример №4
Найти составляющую вектора 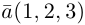
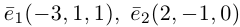
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 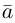

Переходим к вычислениям:
Тогда
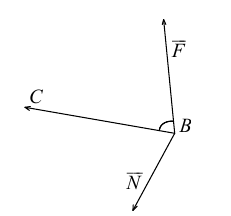
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 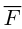
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 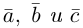
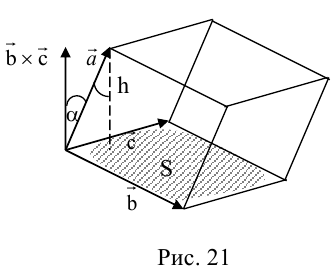
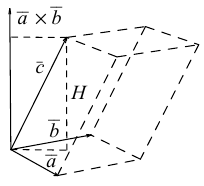
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 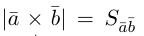
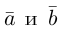
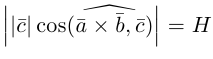
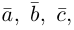
— объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 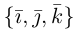
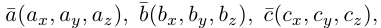
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 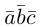
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 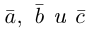
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 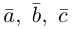
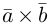
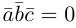
Следствие. Три вектора 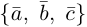
Заметим, кроме того, что, если 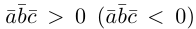
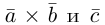
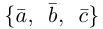
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 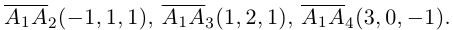
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 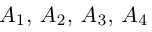
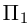
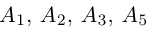
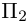
так как первая и третья строки в определителе пропорциональны. Плоскости 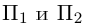
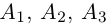
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
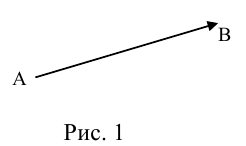
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 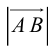
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
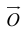
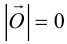
Определение: Векторы 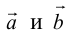
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 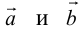
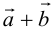
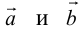
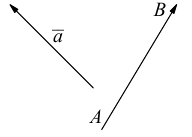
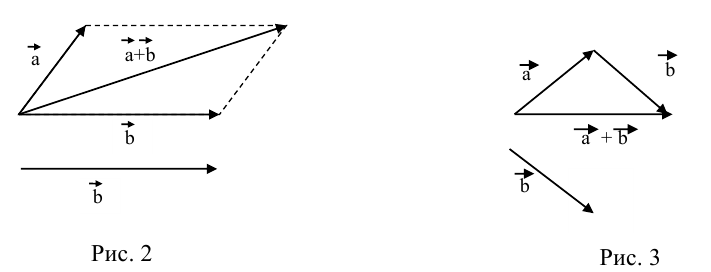
б) Правило треугольника (рис. 3): начало 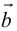
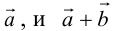
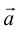
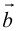
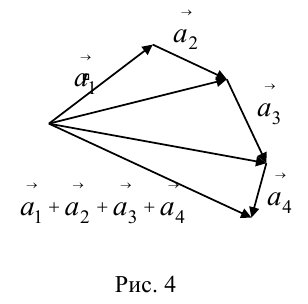
в) Правило сложения нескольких векторов (рис. 4).
Вектор 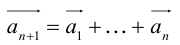
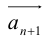
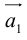
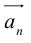
Умножение на число
Определение: Произведением вектора 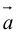
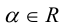
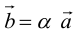
а) 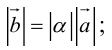
б) 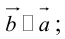
в)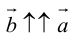
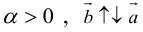
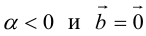
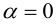
Произведение 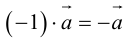
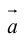
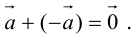
Определение: Разностью 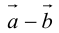
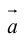
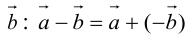
Начала 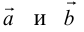
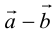
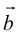
Свойства линейных операций
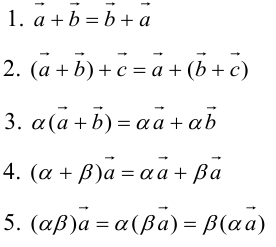
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: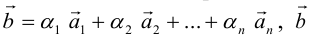
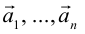
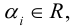
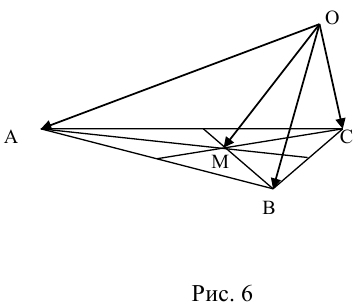
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 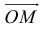
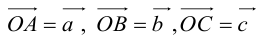
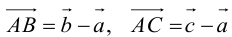
По правилу треугольника 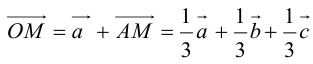
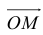
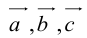
Теорема: Пусть 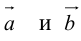
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 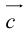
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
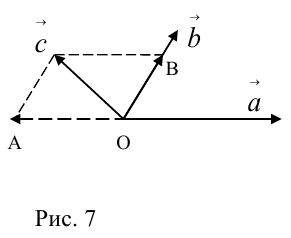
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 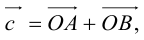
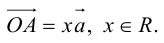
Докажем единственность разложения. Предположим, что 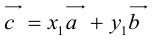
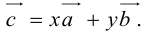
Если 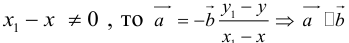
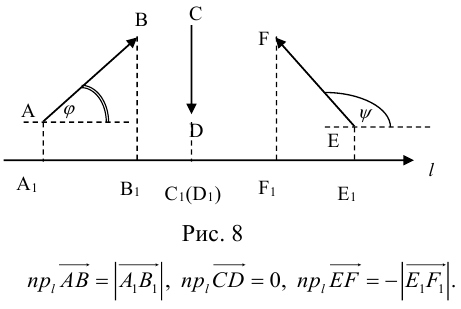
Теорема: Пусть 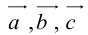
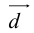
причем единственным образом.
Представление вектора 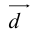
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 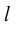
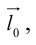
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 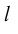
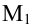
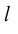
Определение: Ортогональной проекцией вектора 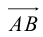
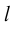
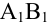
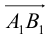
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
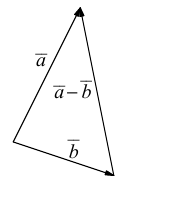
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
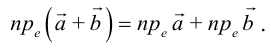
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 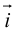
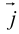

Аналогично в пространственной системе OXYZ 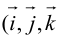
– разложение 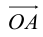
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 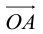
Определение: Координатами вектора 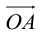
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 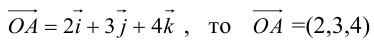
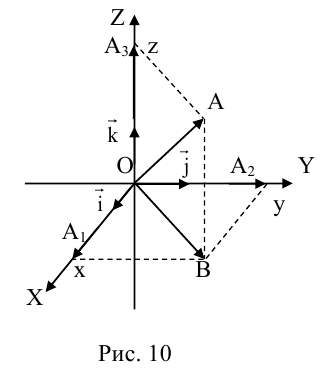
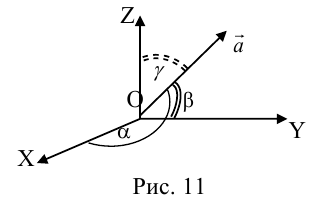
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 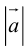
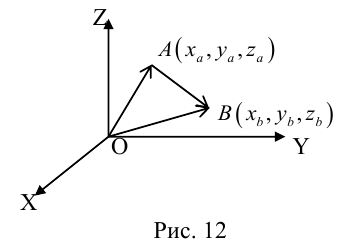
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
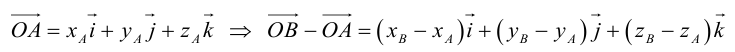
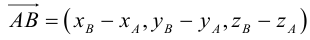
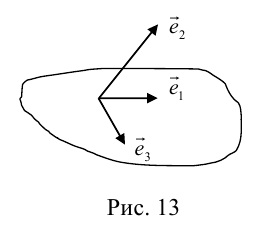
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 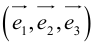
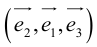
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 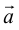
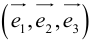
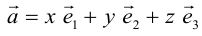
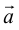
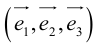
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 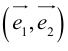
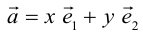
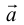
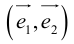
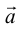
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
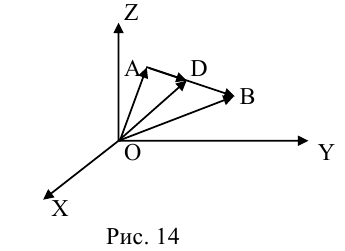
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 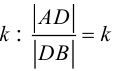
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
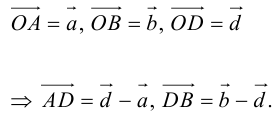
Так как 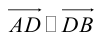
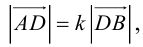
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
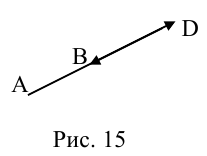
ЗАМЕЧАНИЕ 2. Если k < 0, 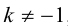
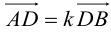
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 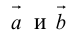
Скалярное произведение обозначается так: 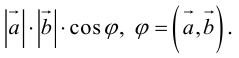
Так как 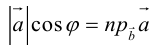
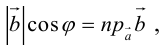
Свойства скалярного произведения
1.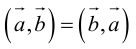
2.
Доказательство:
3.
Доказательство:
а) 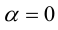
б)
в) 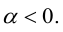
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 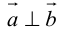
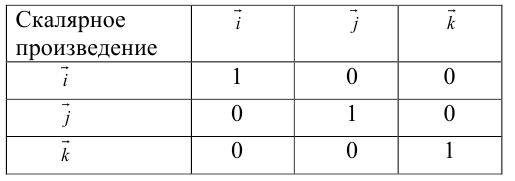
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 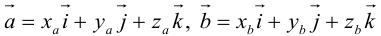
Таким образом,
Пример №8
Найти, при каком значении x векторы 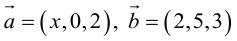
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 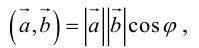
то
Найдем координаты векторов 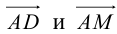
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 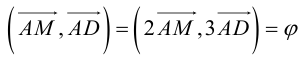
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 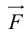
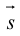
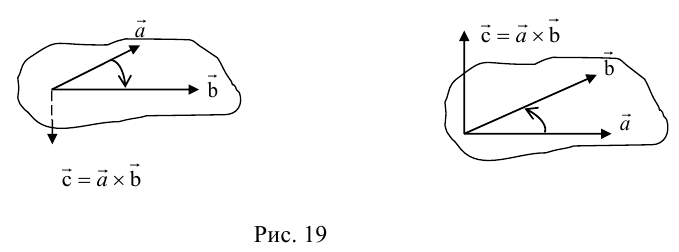
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 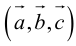
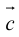
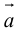
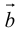
Определение: Векторным произведением вектора 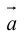
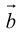
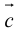
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 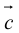
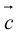
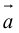
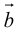
Свойства векторного произведения
1.
Доказательство:
а)пусть 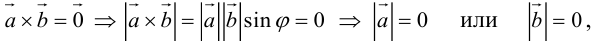
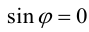
Его направление не определено, поэтому можно считать, что 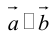
б)пусть
2. 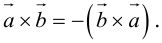
Доказательство: По определению направления векторов 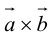
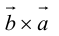
3.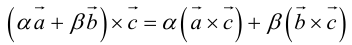
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 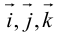
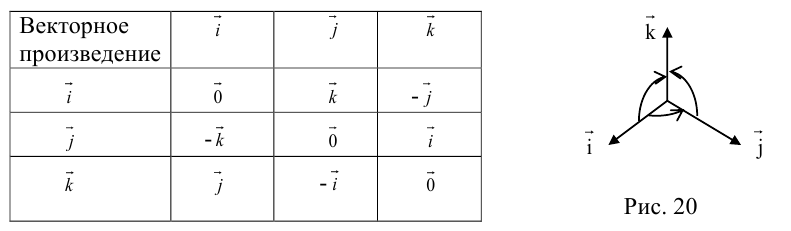
Пусть в некоторой пдск 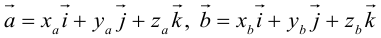
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
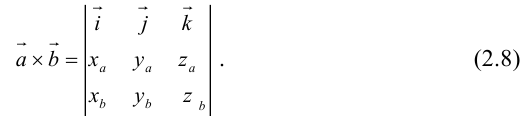
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 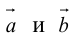
или
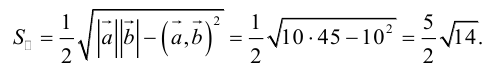
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 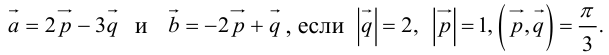
Так как 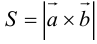
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 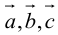
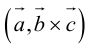
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
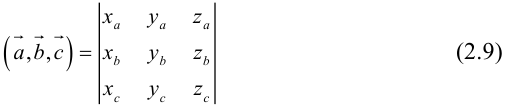
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
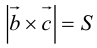
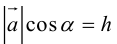
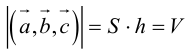
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 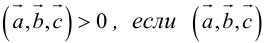
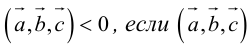
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 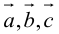
Доказательство: а) 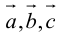
Если 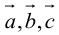
б)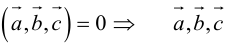
Во всех трех случаях 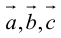
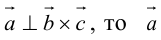
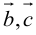
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
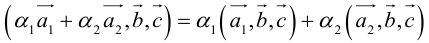
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
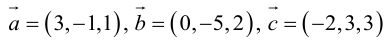
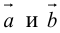
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 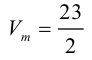

Чтобы найти высоту, воспользуемся формулой
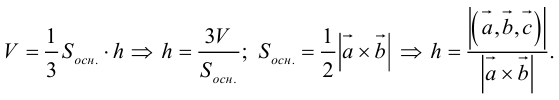
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика























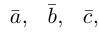
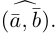
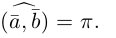
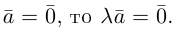
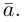
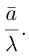
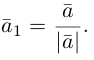
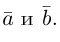
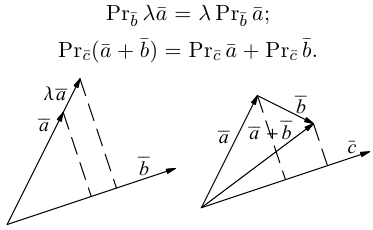
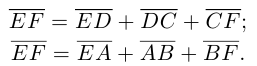
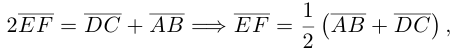
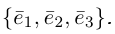
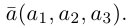
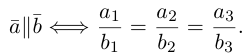
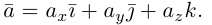
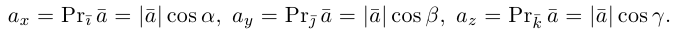
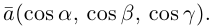
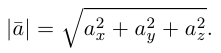
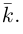

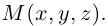
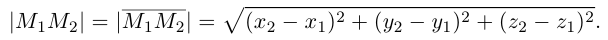
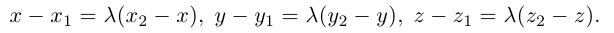
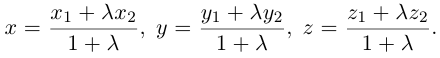
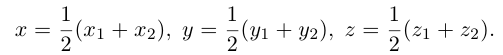
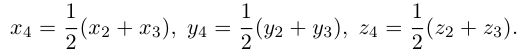
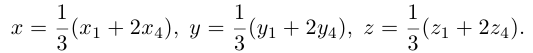
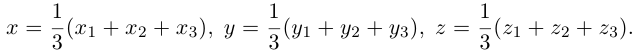


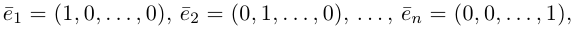
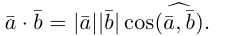
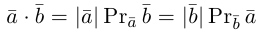
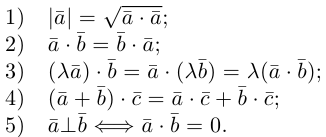
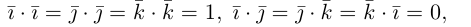
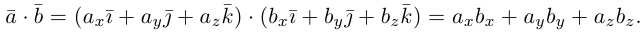
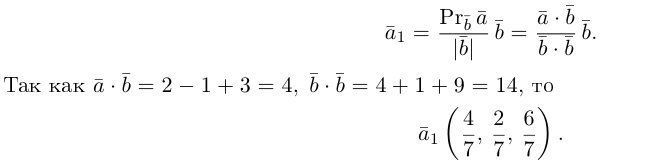
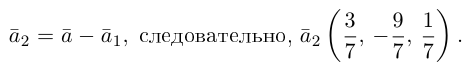
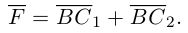
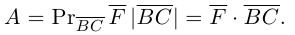
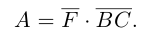
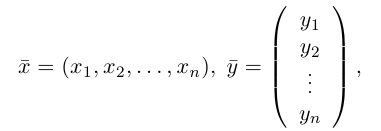
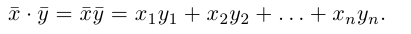
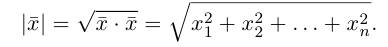
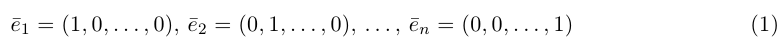
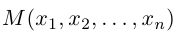

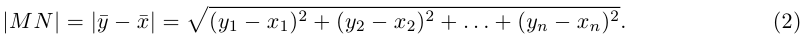
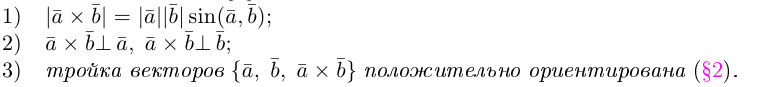
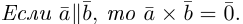
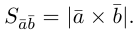
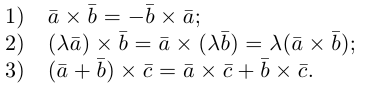
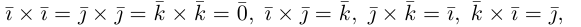
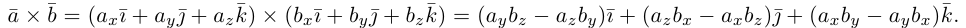
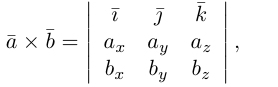
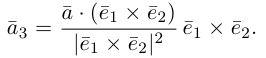
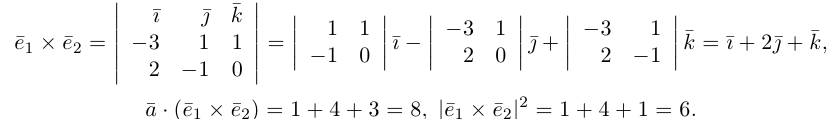
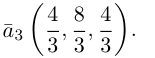
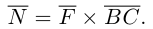
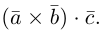
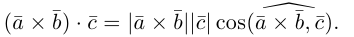
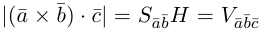
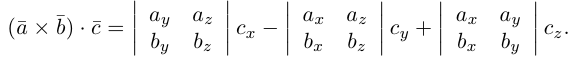
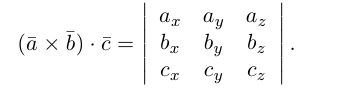
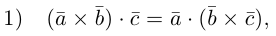
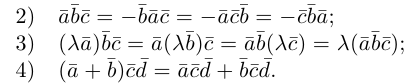
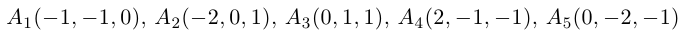
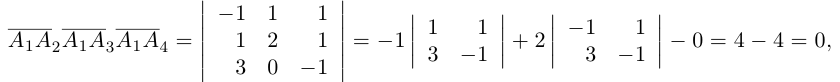
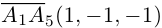
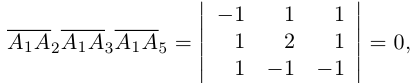
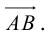
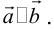

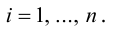
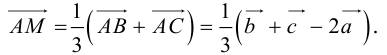
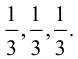
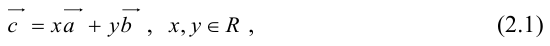
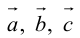 есть два коллинеарных, например:
есть два коллинеарных, например: 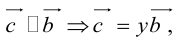
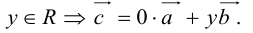
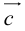 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 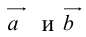 (рис. 7).
(рис. 7). 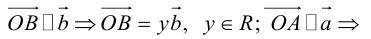
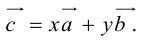
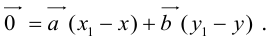
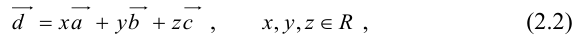
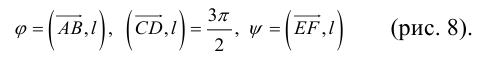
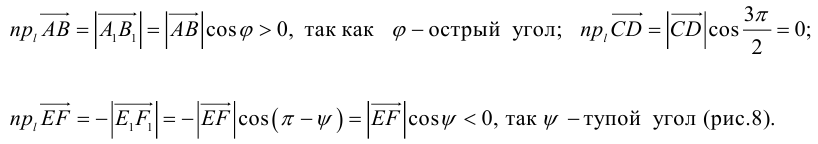
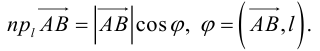
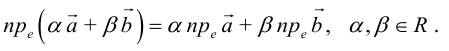
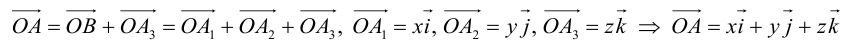
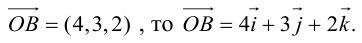
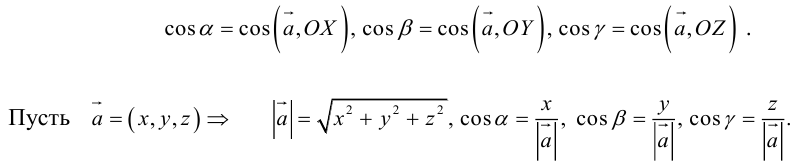
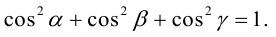
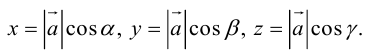
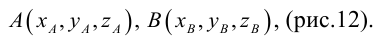
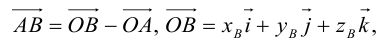
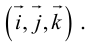
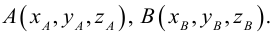

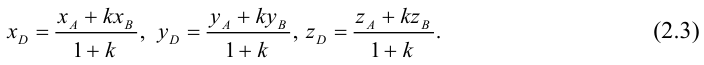
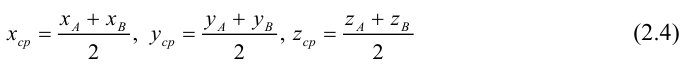
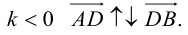
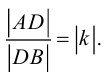
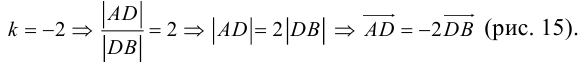
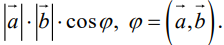
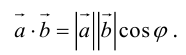
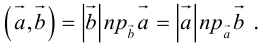
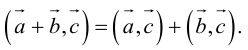
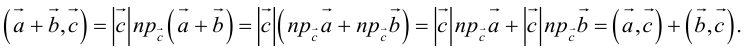
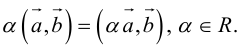
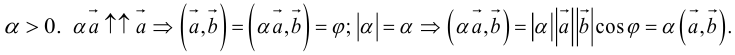
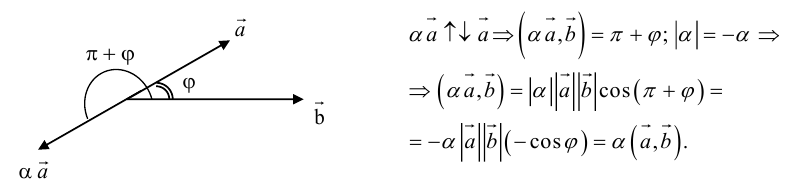
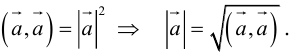
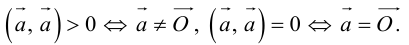
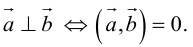
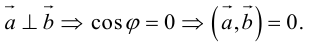
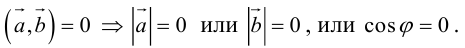
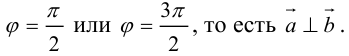
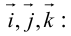
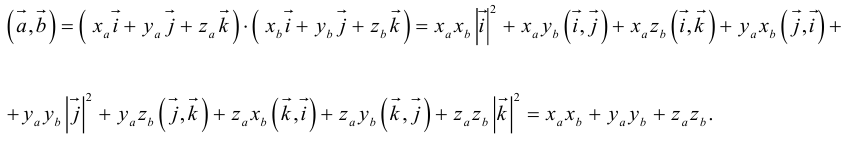

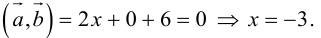
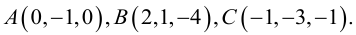

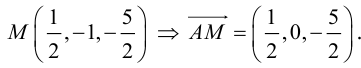
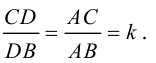
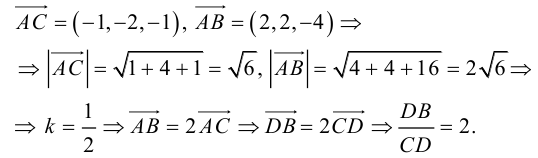
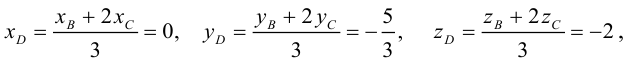
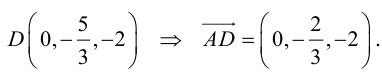
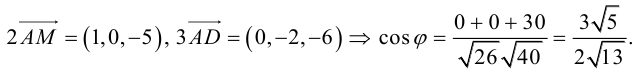
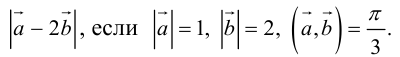
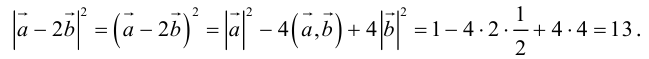
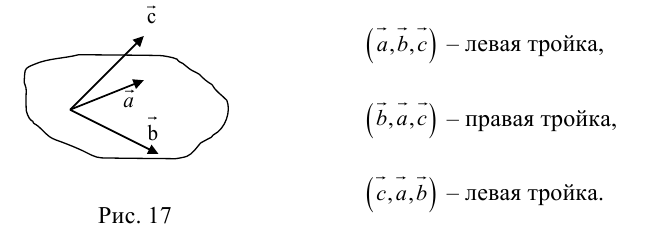
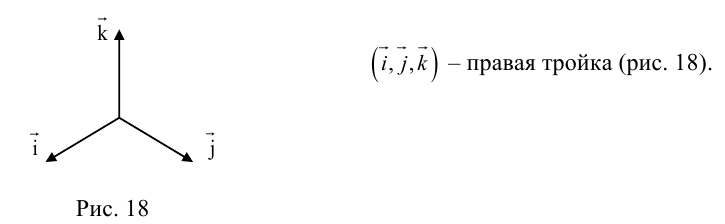
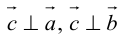 (
(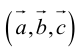 – правая.
– правая.