Лучший ответ
|
|
 |
|
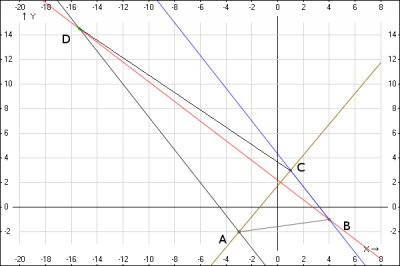
записать уравнение сторон трапеции с вершинами а( -2,2) b( -1,2) c(3,4) d(6,2) высшая математика
С высшей математикой тут явно перебор.
Это четыре прямые проходящие через соответствующие соседние вершины и имеющие область определения ограниченную координатой Х точек вершин. Попробуй сама их вывести. Это не сложно, если вспомнить уравнение прямой на плоскости проходящей через две заданные точки.
Чего-то вы напутали с координатами. Вот что получилось при построении (смотрите картинку). На трапецию никак не тянет.
Уравнение средней линии
Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?
Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.
Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.
1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.
М — середина отрезка AB, N — середина BC.
Составим уравнение прямой MN, например, в виде y=kx+b:
Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.
— середина отрезка AB. Составим уравнение прямой AC:
Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.
Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:
то есть уравнение прямой MN ищем в виде
Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:
Таким образом, уравнение прямой MN
Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.
Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).
Сначала следует определить основания данной трапеции.
Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.
Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),
Уравнение прямой BC: y= -2k+7.
Поскольку угловые коэффициенты прямых равны:
то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.
Составим уравнение прямой MN, M(-1/2;3), N(2;-2):
Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.
Значит уравнение MN ищем в виде y= -2x+b.
Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:
Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
A trapezoid is a type of quadrilateral with two parallel sides. A quadrilateral is a type of polygon with four sides. The sum of four internal angles of a quadrilateral is 360°. Centroid refers to the center point of any figure. It is also known as the geometric center. In a 2D coordinate system, the centroid is always measured with respect to the x-axis and y-axis. In a trapezoid, the centroid is also measured with respect to these two axes.
Centroid of a Trapezoid Formula
A centroid point is the center point of the trapezoid. Centroid is represented in the form of coordinates of the center point of a trapezoid. A horizontal or vertical line through the centroid point divides it into two equal parts. It means, for the height ‘h,’ a center point will be ‘h/2.’ Similarly, the other center point is calculated. These two points form the centroid.
The diagram of a trapezoid is shown below:
Centroid of a figure is given by:
C = [XC, YC]
Where,
XC is the point on the x-axis
YC is the point on the y-axis
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h is the height
p is the base
q is the opposite parallel side
Comparing the values, we get:
XC = h/2
YC =
Sample Problems
Question 1: Find the centroid of a trapezoid with a height of 4m and two parallel sides of 5m and 3m.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 4m
p = 5m
q = 3m
C = [4/2,
]
C = [2, 52/24]
C = [2, 2.17]
Thus, the centroid is [2, 2.17] or 2m with respect to the x-axis and 2.17m with respect to the y-axis.
Question 2: Find the centroid of a trapezoid with a height of 2cm and two parallel sides of 6cm and 4cm.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 2cm
p = 6cm
q = 4cm
C = [2/2,
]
C = [1, 32/30]
C = [1, 1.07]
Thus, the centroid is [1, 1.07] or 1cm with respect to the x-axis and 1.07cm with respect to the y-axis.
Question 3: Find the centroid of a trapezoid with a height of 10m and two parallel sides of 7m and 4m.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 10m
p = 7m
q = 4m
C = [10/2,
]
C = [5, 180/33]
C = [5, 5.45]
Thus, the centroid is [5, 5.45] or 5m with respect to the x-axis and 5.45m with respect to the y-axis.
Question 4: Find the centroid of a trapezoid with a height of 11cm and two parallel sides of 3cm and 2cm.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 1cm
p = 2cm
q = 3cm
C = [1/2,
]
C = [0.5, 7/15]
C = [0.5, 0.47]
Thus, the centroid is [0.5, 0.47] or 0.5cm with respect to x-axis and 0.47cm with respect to y-axis.
Question 5: Find the centroid of a trapezoid with a height of 8m and two parallel sides of 5m and 3m.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 8m
p = 5m
q = 3m
C = [8/2,
]
C = [4, 104/24]
C = [4, 4.33]
Thus, the centroid is [4, 4.33] or 4m with respect to the x-axis and 4.33m with respect to the y-axis.
Question 6: Find the centroid of a trapezoid with a height of 5m and two parallel sides of 7m and 9m.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 5m
p = 7m
q = 9m
C = [5/2,
]
C = [2.5, 115/48]
C = [2.5, 2.4]
Thus, the centroid is [2.5, 2.4] or 2.5m with respect to the x-axis and 2.4m with respect to the y-axis.
Question 7: Find the centroid of a trapezoid with a height of 20cm and two parallel sides of 15cm and 12cm.
Solution:
The formula to calculate the centroid of a trapezoid is given by:
C = [h/2,
]
Where,
h = height
p and q are the two parallel sides
h = 20cm
p = 15cm
q = 12cm
C = [20/2,
]
C = [10, 840/81]
C = [10, 10.37]
Thus, the centroid is [10, 10.37] or 10cm with respect to the x-axis and 10.37cm with respect to the y-axis.
Last Updated :
10 Feb, 2022
Like Article
Save Article
Если у меня есть трапеция, определяемая четырьмя точками (x1, y1), (x2, y2), (x3, y3), (x4, y4) (выбранной как (255, 0), (255, 235), (200, 35) и (200, 235) для примера) , и я произвольно делю его на разделы n на m , например так (простите за грубый рисунок):
Как мне найти координаты (x, y)?
Я пробовал дурачиться с наклоном линий, но мои математические навыки слишком ржавые, чтобы понять это. Любые идеи?
1 ответ
Лучший ответ
Для конкретного случая в соответствии с вашим примером это довольно просто.
Во-первых, местоположение x очень просто. Поскольку вертикали всегда будут параллельны оси y, x — это просто ширина x, деленная на количество секций:
x = x1+((x2-x1)/a*xa)
Где:
- x = координата результата
- x1, x2 = края трапеции
- a = количество секций
- xa = координата x в секциях
Примечание: я выбрал a, чтобы избежать путаницы с символом наклона: m.
Для y это немного сложнее. Сначала нам нужно найти координату, которая находится на верхней и нижней линиях трапеции. Для этого мы используем стандартное линейное уравнение:
y = mx+c
Найти m просто. Это просто Dy / Dx:
m = (y2-y1)/(x2-x1)
Чтобы получить c, мы просто подставляем x, y и m в формулу:
c = y-mx
Как только мы получим это, подставим ранее найденное значение x в формулу, чтобы получить координату y. Сделайте это дважды, чтобы получить точки в верхней и нижней строках:
1 A 2
x------------x--------------x
| | |
| xC |
| | |
x------------x--------------x
3 B 4
Все вместе (псевдокод):
coordinateFromSection (x1 y1 x2 y2 x3 y3 x4 y4 gridX gridY sectionX sectionY) {
xC = x1+((x2-x1)/gridX*sectionX)
// top line:
m = (y2-y1)/(x2-x1)
c = y1-(m*x1)
yA = m*xC + c
// bottom line:
m = (y4-y3)/(x4-x3)
c = y3-(m*x3)
yB = m*xC + c
// Find yC by dividing line AB by gridY
yC = yA+((yB-yA)/gridY*sectionY)
return (xC yC)
}
Все приведенные выше вычисления предполагают, что (0,0) находится в верхнем левом углу экрана.
3
slebetman
4 Мар 2013 в 08:51
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти координаты вершины
|
|||
|
Даны вершины А(-2;-2) В(5;-1) и точка С(2;3) трапеции АВСD (AD ПАРАЛЕЛЬНО ВС). Известно что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции чертеж((((
|
||
| Вернуться к началу |
|
||
|
Andy |
Заголовок сообщения: Re: Найти координаты вершины
|
|
mad_math писал(а): Если это школьная задача, то её не через уравнения прямых решают. mad_math, если не ошибаюсь, уравнение прямой, проходящей через две точки, в школе проходят. Но, конечно же, можно воспользоваться и сложением векторов. Пусть, однако, автор вопроса отзовётся — тогда разберёмся.
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Найти координаты вершины
|
|
Andy писал(а): mad_math, если не ошибаюсь, уравнение прямой, проходящей через две точки, в школе проходят. Да, но в курсе алгебры и мат.анализа, а не геометрии. В геометрии проходят координатный метод.
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Найти координаты вершины
|
|
Andy писал(а): но векторы-то в курсе геометрии проходят Да. Это и есть координатный метод. Andy писал(а): Впрочем, автор вопроса, похоже не интересуется нашим обсуждением. Этточно. Я даже не уверена, что автор вопроса не ошиблась разделом.
|
|
| Вернуться к началу |
|