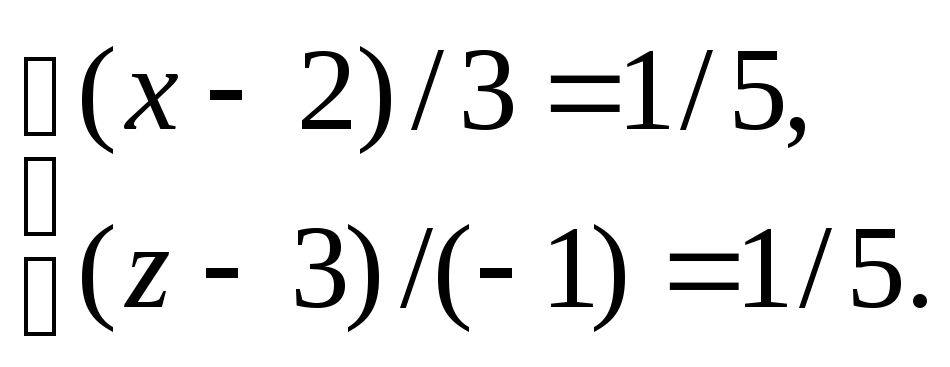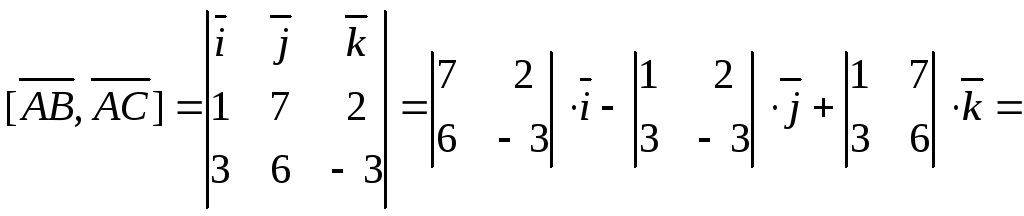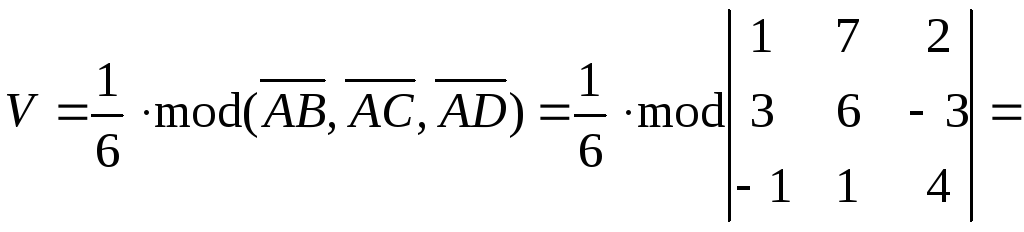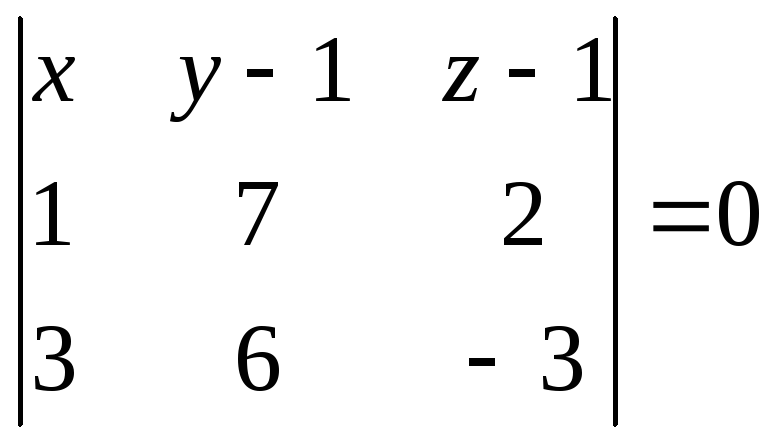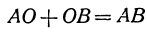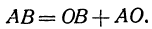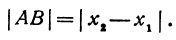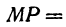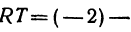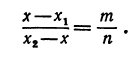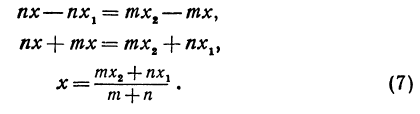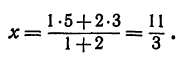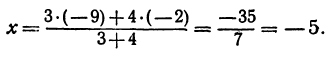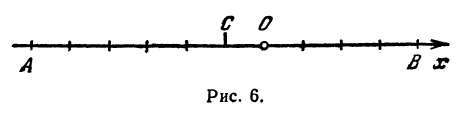Деление отрезка в данном отношении
Пусть даны точки
и
.
Требу-ется
найти координаты точки
,
делящей отрезок прямой, заключенный
между М1
и М2,
в отношении
,
(рис. 7.6).
Рис. 7.6
Рассмотрим
векторы
и
.
Они коллинеарны и одинаково направлены,
то есть могут отли-чаться только длиной.
По условию
,
поэтому
или
в координатной форме
.
Из
равенства этих двух векторов следует
равенство их соот-ветствующих координат:
,
,
Отсюда
,
,
,
В частности, если
точка М
делит отрезок М1М2
пополам, то
и
,
,
,
то есть координаты
точки, делящей отрезок пополам, равны
полусуммам соответствующих координат
концов отрезка.
Пример 7.12.
Найти
координаты точки М,
делящей по-полам отрезок прямой
,
заключенный между плоскостями
Oxz
и Оxу.
Решение.
Найдем точку пересечения прямой с
плоскостью
Oxz,
полагая в
уравнениях прямой
.
Тогда получим
или
Из
последней системы находим
,
.
Эти коор-динаты вместе с
определяют точку
Анало-гично, полагая в уравнениях прямой
,
имеем:
или
откуда
,
.
Получим
точку
пересечения прямой с плоскостью Оxу.
Зная
координаты концов
и
отрезка АВ,
по формулам деления отрезка пополам
определим координаты
точки М
– середины отрезка АВ:
;
;
Итак,
–
искомая
точка.
Пример
7.13.
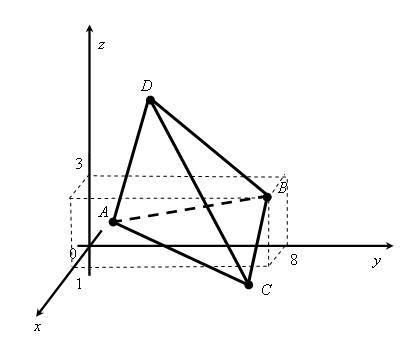
Даны координаты вершин пирамиды
,
,
,
.
Найти: 1) длины ребер АВ
и AC;
2) угол между ребрами АВ
и АС;
3) площадь грани АВС;
4) объем пирамиды ABCD;
5) уравнение прямой АВ;
6) уравнение плоскости АВС;
7) уравнение высоты пирамиды, опущенной
на грань АВС.
Сделать чертеж.
Решение
-
Длина
ребра AB
совпадает с длиной вектора
,
поэтому определим координаты векторов
и
,
.
Длина
вектора равна корню квадратному из
суммы квадратов его координат, то есть
-
Угол
между ребрами AB
и AC
совпадает с углом между векторами
и
,
который можно определить по формуле:
,
.
-
Грань
ABC
представляет собой треугольник, его
пло-щадь найдем через векторное
произведение:
так
как
.
-
Объем
пирамиды вычислим по формуле:
.
Здесь
-
Уравнение
прямой, проходящей через точки А,
В,
имеет вид:
,
то есть
.
-
Уравнение
плоскости ABC
определим из равенства
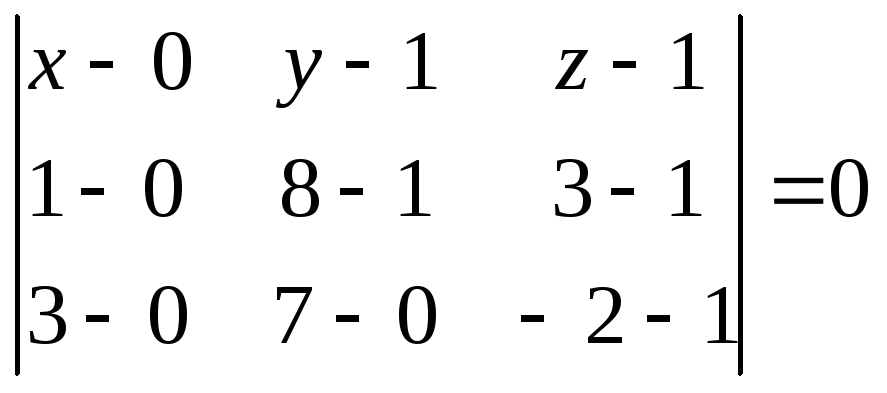
или
.
-
Так
как высота – это прямая, перпендикулярная
плос-кости ABC,
ее направляющим вектором будет
вектор-нормаль
плоскости
ABC,
тогда уравнение высоты имеет вид:
.
Выполним
чертеж (рис. 7.5).
Рис. 7.5
Тема 8. Функции. Теория пределов Понятие функции
В теме 5 мы уже
встречались с понятием функции, информация
о которой основывалась на материале из
школьного курса математики. Здесь это
понятие получит свое дальнейшее развитие.
Пусть на действительной
оси R
заданы два числовых множества
и
.
Определение.
Будем говорить, что на множестве X
задана функция
f
действительной переменной x,
если известен закон (отображение), по
которому каждому значению
по закону f
ставится в соответствие единственное
значение
и обозначается
.
Переменная x
называется аргументом функции f,
множество X
– областью определения функции,
переменная y
– значением функции или зависимой
переменной, а множество Y
– областью значений функции.
Замечание.
Область Y
значений функции обычно не указыва-ется,
так как множество принимаемых значений
функции определяет сам закон.
Допускаются
многозначные функции (то есть одному x
соответствует более одного значения
y).
Обычно эти случаи оговариваются особо.
Замечание.
Для обозначения функциональной
зависимос-ти вместо символа функции f
можно использовать любую дру-гую букву
(но не число) любого алфавита.
Определение.
Совокупность всех значений независимой
переменной х,
для которых функция
определена, назы-вается областью
определения,
или областью существования функции, и
обозначается
.
Определение.
Пусть задана функция
.
Тогда
называется значением
этой функции при
Пример 8.1.
Найти значения
функции
.
Решение.
Вычислим значения функции при заданных
значениях аргумента
;
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:
хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),
где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).
Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:
хС = (хА + хВ)/2, уС = (уА + уВ)/2.
Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.
1. Поиск координат середины некоторого отрезка, по заданным координатам его концов
Пример 1.
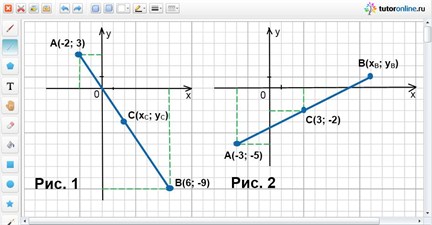
Точки А(-2; 3) и В(6; -9) – концы отрезка АВ. Найти точку С, являющиеся серединой отрезка АВ.
Решение.
В условии задачи задано, что хА = -2; хВ = 6; уА = 3 и уВ = -9. Требуется найти С(хС ; уС).
Применяя формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
хС = (-2 + 6)/2 = 2, уС = (3 + (-9))/2 = -3.
Таким образом, точка С, являющаяся серединой отрезка АВ, имеет координаты (-2; 3) (рис. 1).
2. Вычисление координат конца некоторого отрезка, зная координаты его середины и другого конца
Пример 2.
Одним концом отрезка АВ является точка А, с координатами (-3; -5), а его серединой точка С(3; -2). Вычислите координаты второго конца отрезка – точки В.
Решение.
По условию задачи становится ясно, что хА = -3; уА = -5; хС = 3 и уС = -2.
Подставив эти значения в формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
3 = (-3 + хВ)/2 и
-2 = (-5 + уВ)/2.
Решив первое уравнение относительно хВ и второе относительно уВ, найдем: хВ = 9 и уВ = 1, получается, что нужная точка В будет задаваться координатами (9; 1) (рис. 2).
3. Вычисление координат вершин некоторого треугольника по заданным координатам середин его сторон
Пример 3.
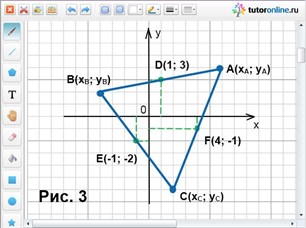
Серединами сторон треугольника АВС являются точки D(1; 3), E(-1; -2) и F(4; -1). Найти координаты вершин А, В и С данного треугольника.
Решение.
Пусть точка D и есть середина стороны АВ, точка Е – середина ВС и точка F – середина сторона АС (рис. 3). Необходимо найти точки А, В и С.
Обозначаем вершины треугольника через А(хА; уА), В(хВ; уВ) и С(хС; уС) и зная координаты точек D, Е и F, по формулам хС = (хА + хВ)/2, уС = (уА + уВ)/2 получим:
{1 = (хА + хВ)/2,
{-1 = (хВ + хС)/2,
{4 = (хА + хС)/2,
и
{3 = (уА + уВ)/2,
{-2 = (уВ + уС)/2,
{-1 = (уА + уС)/2.
Приведем уравнения к целому виду:
{хА + хВ = 2,
{хВ + хС = -2,
{хА + хС = 8,
и
{уА + уВ = 6,
{уВ + уС = -4,
{уА + уС = -2.
Решив системы, получим:
хА = 6; хВ = -4; хС = 2.
уА = 4; уВ = 2; уС = -6.
Точки А(6; 4), В(-4; 2) и С(2; -6) и есть необходимые вершины треугольника.
4. Вычисление координат точек, которые делят отрезок в определенном отношении, по заданным координатам концов этого отрезка
Пример 4.
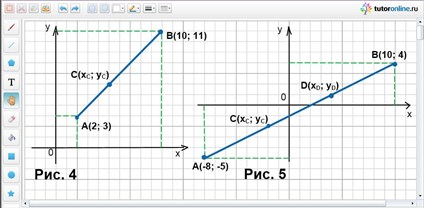
Отрезок АВ поделен точкой С в отношении 3 : 5 (считая от точки А к точке В). Концы отрезка АВ – точки А(2; 3) и В(10; 11). Найти точку С.
Решение.
В условии задачи сказано, что хА = 2; хВ = 10; уА = 3; уВ = 11; λ = АС/СВ = 3/5. Найти С(хС; уС) (рис. 4).
по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (2 + 3/5 · 10) / (1 + 3/5) = 5 и уС = (3 + 3/5 · 11) / (1 + 3/5) = 6. Таким образом, имеем С(5; 6).
Выполним проверку: АС = 3√2, СВ = 5√2, λ = АС/СВ = 3√2/5√2 = 3/5.
Замечание. В условии задачи указано, что деление отрезка производится в заданном отношении от точки А к точке В. Если бы это не уточнялось, то задача имела бы два решения. Второе решение: деление отрезка от точки В к точке А.
Пример 5.
Некоторый отрезок АВ разделен в отношении 2 : 3 : 5 (считая от точки А к точке В), его концы – есть точки с координатами А(-11; 1) и В(9; 11). Найти точки деления данного отрезка.
Решение.
Обозначим точки деления отрезка от А к В через С и D. В условии задачи дано, что
хА = -11; хВ = 9; уА = 1; уВ = 11. Найти С(хС; уС) и D(хD; уD), если АС : СD : DB = 2 : 3 : 5.
Точка С делит отрезок АВ в отношении λ = АС/СВ = 2/(3 + 5) = 2/8 = 1/4.
По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (-11 + ¼ · 9) / (1 + 1/4) = -7 и уС = (1 + ¼ · 11) / (1 + 1/4) = 3.
Таким образом, С(-7; 3).
Точка D – есть середина отрезка АВ. Применив формулы хD = (хА + хВ)/2, уD = (уА + уВ)/2, найдем:
хD = (-11 + 9)/2 = -1, уD = (1 + 11)/2 = 6. Значит, D имеет координаты (-1; 6).
5. Вычисление координат точек, которые делят отрезок, если заданы координаты концов этого отрезка и число частей, на которые этот отрезок разделен
Пример 6.
Концы отрезка – точки А(-8; -5) и В(10; 4). Найти точки С и D, которые делят этот отрезок на три равные части.
Решение.
Из условия задачи известно, что хА = -8; хВ = 10; уА = -5; уВ = 4 и n = 3. Найдем С(хС; уС) и D(хD; уD) (рис. 5).
Найдем точку С. Она делит отрезок АВ в отношении λ = 1/2. Деление производим от точки А к точке В. По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) имеем:
хС = (-8 + ½ · 10) / (1 + 1/2) = -2 и уС = (-5 + ½ · 4) / (1 + 1/2) = -2. Таким образом, С(-2; -2).
Деление отрезка СВ выполняется в отношении 1 : 1, поэтому используем формулы
хD = (хА + хВ)/2, уD = (уА + уВ)/2:
хD = (-2 + 10)/2 = 4, уD = (-2 + 4)/2 = 1. Таким образом, D(4; 1).
Точки деления С(-2; -2) и D(4; 1).
Замечание: Точку D можно найти, производя деление отрезок АВ в отношении 2 : 1. В таком случае надо будет снова применить формулы хD = (хА + λхВ) / (1 + λ), уD = (уА + λуВ) / (1 + λ).
Пример 7.
Точки А(5; -6) и В(-5; 9) – концами отрезка. Найти точки, которые поделят данный отрезок на пять равных частей.
Решение.
Пусть последовательные точки деления от А к В будут С(хС; уС), D(хD; уD), Е(хE; уE) и F(хF; уF). В условия задачи сказано, что хА = 5; хВ = -5; уА = -6; уВ = 9 и n = 5.
Найдем по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) точку С. Она делит отрезок АВ в отношении λ = 1/4:
хС = (5 + 1/4 · (-5)) / (1 + 1/4) = 3 и уС = (-6 + 1/4 · 9) / (1 + 1/4) = -3, получаем, что точка С имеет координаты (3; -3).
Деление отрезка АВ точкой D производится в отношении 2 : 3 (т.е. λ = 2/3), поэтому:
xD = (5 + 2/3 · (-5)) / (1 + 2/3) = 1 и уD = (-6 + 2/3 · 9) / (1 + 2/3) = 0, значит D(1; 0).
Найдем точку Е. Она делит отрезок АВ в отношении λ = 2/3:
XЕ = (5 + 3/2 · (-5)) / (1 + 3/2) = -1 и уЕ = (-6 + 3/2 · 9) / (1 + 3/2) = 3. Таким образом, Е(-1; 3).
Точка F делит отрезок АВ в отношении λ = 4/1, поэтому:
XF = (5 + 4 · (-5)) / (1 + 4) = -3 и уF = (-6 + 4 · 9) / (1 + 4) = 6, F(-3; 6).
Точки деления С(-2; -2); D(4; 1); Е(-1; 3) и F(-3; 6).
Остались вопросы? Не знаете, как решить задачу на деление отрезка?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Координаты на прямой:
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:
Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число 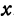
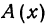
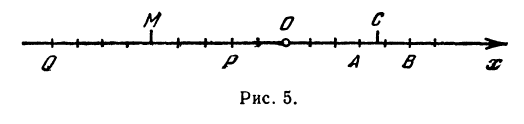
Указанные на рис. 4 точки имеют следующие координаты: 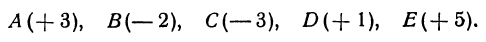
Если даны точки 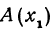
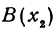
т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
- Заказать решение задач по высшей математике
Пример:
Если даны точки 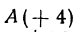
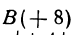
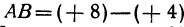
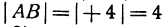
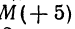
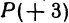
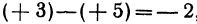
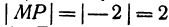
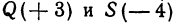
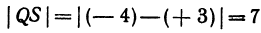
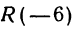
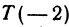
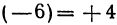
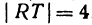
Пример:
Начало отрезка АВ находится в точке 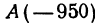
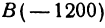
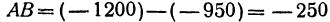
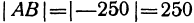
Пример:
На координатной оси даны две точки: 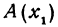
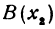
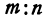
Обозначая координату искомой точки С через 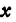
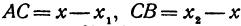
Решая последнее уравнение относительно 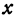
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка 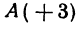
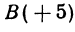
Решение:
Здесь 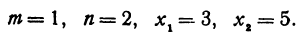
Пример:
Найти точку 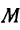
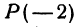
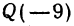
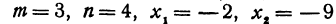
Решение:
Если 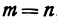
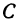
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками 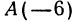
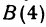
Решение:
Применяя формулу (8), получим, 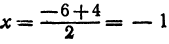
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
1) Координаты вектора равны разности соответствующих координат точек его конца и начала ab{х2-х1;y2-y1}
В нашем случае вектор АВ имеет координаты АВ{3-1;6-(-2)} или АВ{2;8}.
Вектор СВ имеет координаты СВ{5-3;(-2-6)} или СВ{2;-8}.
Ответ: АВ{2;8}, СВ{2;-8}.
2)А координаты середины отрезка AB найдем по формуле
М = (Аx + Вx)/2, y = (Аy + Вy)/2.
В нашем случае Хм(1+3)/2=2, Yм=(-2+6)/2=2. Ответ: М(2;2)