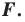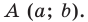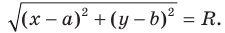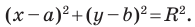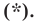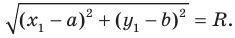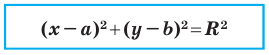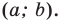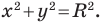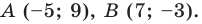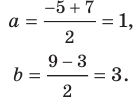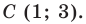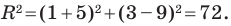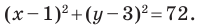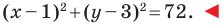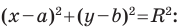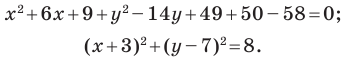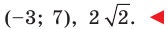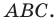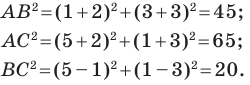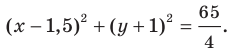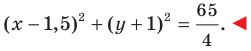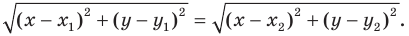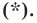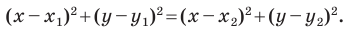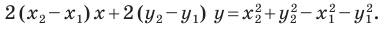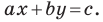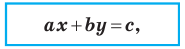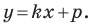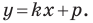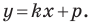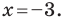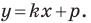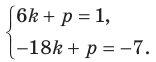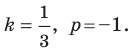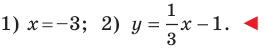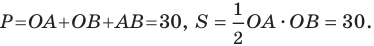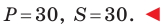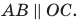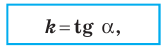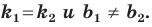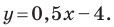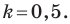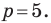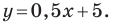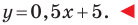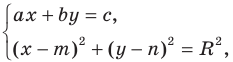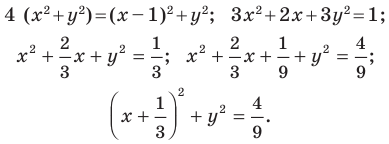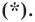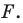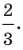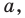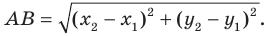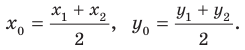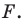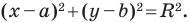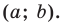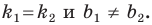Определение.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc — za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
На этой странице можно рассчитать координаты середины отрезка как на плоскости, так и в пространстве. Введите координаты точек и получите ответ, а также подробное решение с помощью наших онлайн-калькуляторов.
Задача нахождения координат середины отрезка довольно часто возникает при решении задач, связанных с нахождением средней линии, медианы а также других вычислениях. На нашем сайте также можно рассчитать длину отрезка, заданного координатами.
Середина отрезка — точка, расположенная на отрезке на равном расстоянии от его конечных точек.
Формула для нахождения координат середины отрезка на плоскости
{x_c=dfrac{x_a + x_b}{2}; ; y_c=dfrac{y_a + y_b}{2}}
xa и ya — координаты первой точки A,
xb и yb — координаты второй точки B,
xc и yc — координаты середины отрезка (точка C).
Формула для нахождения координат середины отрезка в пространстве
{x_c=dfrac{x_a + x_b}{2}; ; y_c=dfrac{y_a + y_b}{2}; ; z_c=dfrac{z_a + z_b}{2}}
xa, ya и za — координаты первой точки A,
xb, yb и zb— координаты второй точки B,
xc, yc и zc — координаты середины отрезка (точка C).
Примеры задач на вычисление середины отрезка
Задача 1
Найдите координаты середины отрезка АВ,если А(-2,3) и В(6,-3).
Решение
Подставим координаты концов отрезка в формулы.
x_c=dfrac{x_a + x_b}{2} = dfrac{-2 + 6}{2} = dfrac{4}{2} = 2
y_c=dfrac{y_a + y_b}{2} = dfrac{3 + (-3)}{2} = dfrac{0}{2} = 0
Мы получили координаты середины отрезка — C(2, 0).
Ответ: C(2, 0)
Калькулятор середины отрезка поможет проверить результат.
Задача 2
Дано: A(1, -1, 2), B(3, 1, -2). Найдите координаты середины отрезка AB.
Решение
Воспользуемся формулами координат середины отрезка в пространстве, подставив в них значение координат концов отрезка.
x_c=dfrac{x_a + x_b}{2} = dfrac{1 + 3}{2} = dfrac{4}{2} = 2
y_c=dfrac{y_a + y_b}{2} = dfrac{-1 + 1}{2} = dfrac{0}{2} = 0
z_c=dfrac{z_a + z_b}{2} = dfrac{2 + (-2)}{2} = dfrac{0}{2} = 0
Мы получили координаты середины отрезка — C(2, 0, 0).
Ответ: C(2, 0, 0)
Проверка
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
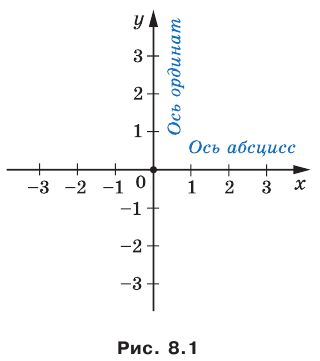
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 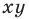
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 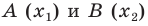
Научимся находить расстояние между точками 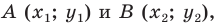
Рассмотрим случай, когда отрезок 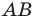
Через точки 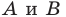
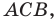
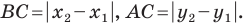
Тогда формулу расстояния между точками 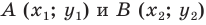
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 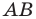
Пусть 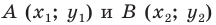
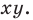
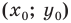
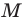
Рассмотрим случай, когда отрезок 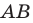
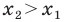
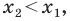
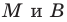
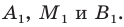
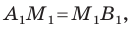
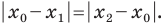
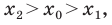
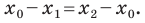

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 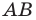
Пример №1
Докажите, что треугольник с вершинами в точках 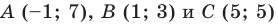
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 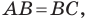
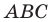
Поскольку 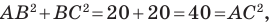
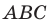
Пример №2
Точка 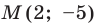
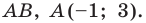
Решение:
Обозначим 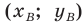
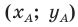
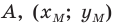
Поскольку 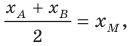
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 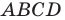
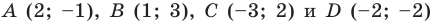
Решение:
Пусть точка 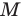
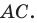
Следовательно,
Пусть точка 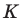
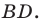
Следовательно,
Таким образом, точки 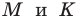
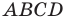
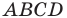
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 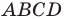
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 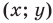
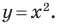
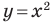
Определение. Уравнением фигуры 
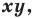
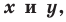
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
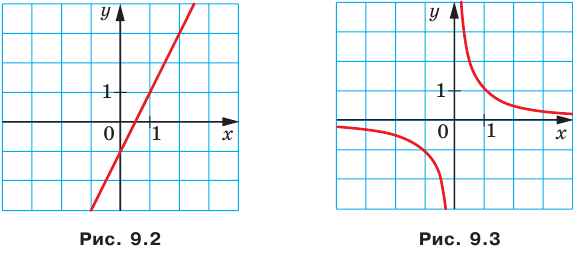
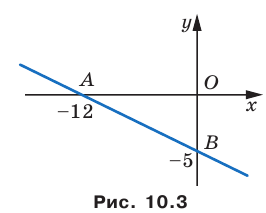
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 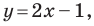
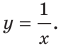
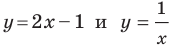
Если данное уравнение является уравнением фигуры 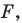
Пользуясь этими соображениями, выведем уравнение окружности радиуса 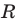
Пусть 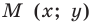
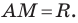
Отсюда
Мы показали, что координаты 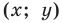
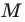
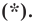
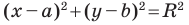
Пусть пара чисел 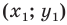
Тогда 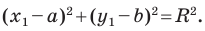
Это равенство показывает, что точка 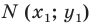
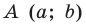
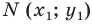
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 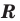
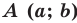
Верно и такое утверждение: любое уравнение вида 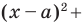
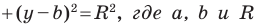
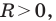
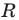
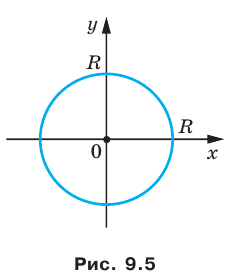
Если центром окружности является начало координат (рис. 9.5), то 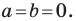
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 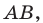
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 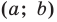
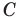
Следовательно,
Радиус окружности 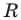
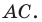
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 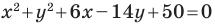
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 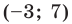
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 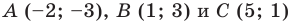
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 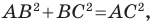
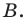
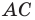
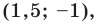
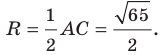
Ответ:
Уравнение прямой
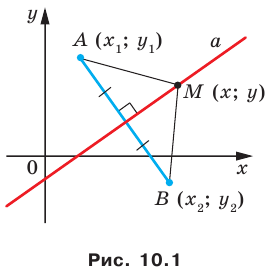
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 
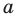
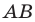
Пусть 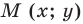
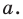
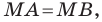
Мы показали, что координаты 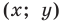
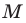
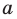
Теперь покажем, что любое решение уравнения 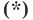
Пусть 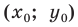
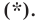
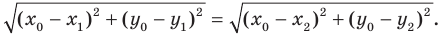
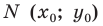
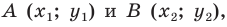
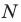
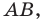
Итак, мы доказали, что уравнение 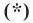
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 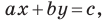
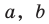
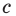
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 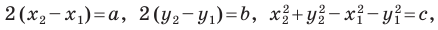
Поскольку точки 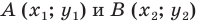
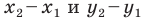
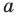
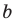
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 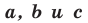
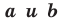
Верно и такое утверждение: любое уравнение вида 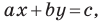
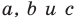
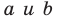
Если 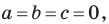
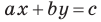
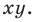
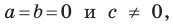
Из курса алгебры 7 класса вы знаете, что уравнение вида 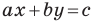
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 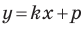
Перепишем уравнение 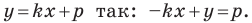
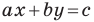
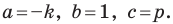
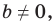
А любую ли прямую на плоскости можно задать уравнением вида 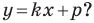
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 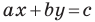
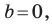
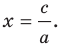
Если 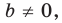
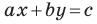
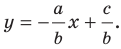
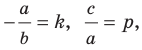
Следовательно, если 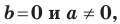
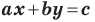
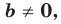
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 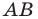
2) Поскольку данные точки имеют разные абсциссы, то прямая 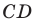
Подставив координаты точек 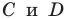
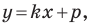
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 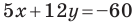
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 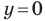
С осью ординат: при 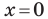
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 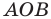
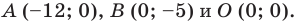
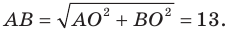
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 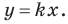
Покажем, что прямые 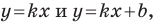
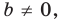
Точки 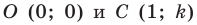
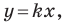
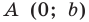
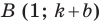
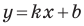
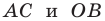
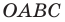
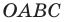
Теперь мы можем сделать такой вывод: если 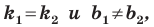
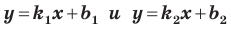
Пусть прямая 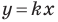
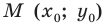
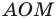
Если прямая 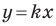
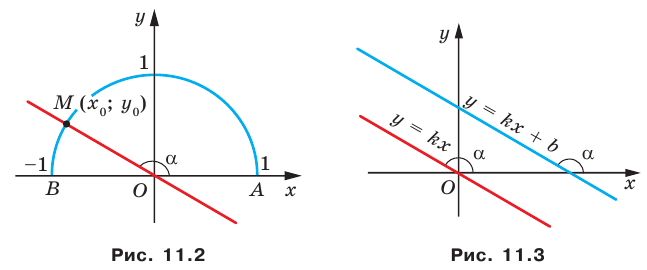
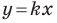
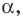
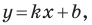
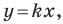
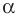
Рассмотрим прямую 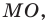
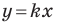
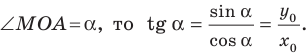
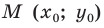
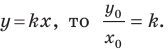
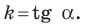
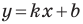
где 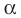
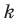
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 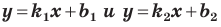
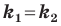
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 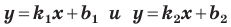
Пример №9
Составьте уравнение прямой, которая проходит через точку 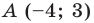
Решение:
Пусть уравнение искомой прямой 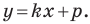
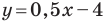
Следовательно, искомое уравнение имеет вид 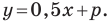
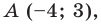
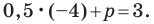
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 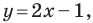
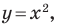
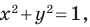
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 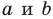
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 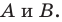
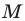
Это серединный перпендикуляр отрезка 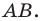
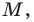
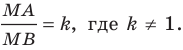
Плоскость, на которой отмечены точки 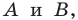
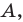
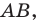
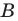
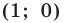
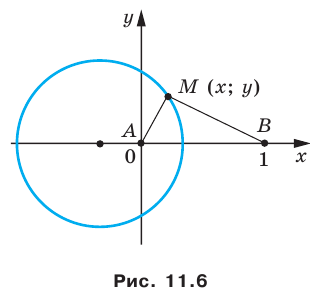
Пусть 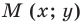
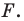
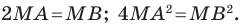
Следовательно, если точка 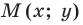
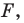
Пусть 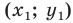
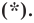
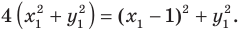
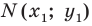
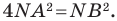
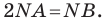
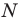
Таким образом, уравнением фигуры 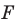
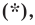
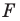
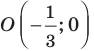
Мы решили задачу для частного случая, когда 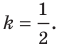
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 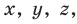
Справочный материал
Расстояние между двумя точками
Расстояние между точками 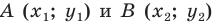
Координаты середины отрезка
Координаты 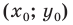
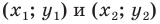
Уравнение фигуры
Уравнением фигуры 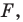
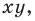
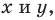
1) если точка принадлежит фигуре 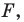
2) любое решение 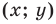
Уравнение окружности
Уравнение окружности радиуса 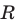
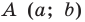
Любое уравнение вида 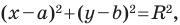
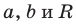
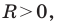
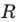
Уравнение прямой
Уравнение прямой имеет вид 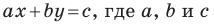
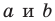
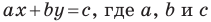
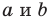
Если 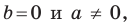
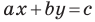
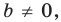
Угловой коэффициент прямой
Коэффициент 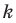
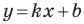
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 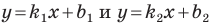
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Отрезок – часть прямой (или множество точек, расположенных на одной прямой), ограниченная двумя точками с определенными параметрами в двухмерной системе координат.
То есть, отрезок АВ имеет координаты:
• А (x1; y1);
• В (x2;y2).
Координаты середины отрезка – точки (С) – вычисляются по формуле: сумму абсцисс (Х1+Х2) и ординат (Y1 + Y2) точек А и В, поделить пополам. Соответственно, в трехмерной системе добавляются координаты оси (Z).
Нахождение середины отрезка очень важно для решения геометрических задач, доказательства теорем.Чтобы не рассчитывать данные по формулам, определяя середину отрезка, проще воспользоваться онлайн-калькулятором. В соответствующие поля вводятся данные X, Y, Z и вычисляются координаты точки, которая является серединой отрезка, расположенного на плоскости или в трехмерном пространстве.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Координаты середины отрезка
Содержание:
- Что такое середина отрезка
-
Правила нахождения координат середины отрезка, формулы
- Середина отрезка на координатной прямой
- Середина отрезка на плоскости
- Середина отрезка в пространстве
- Метод с использованием координат радиус-векторов концов отрезка
- Примеры решения задач
Что такое середина отрезка
Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.
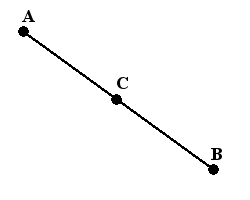
Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.
Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
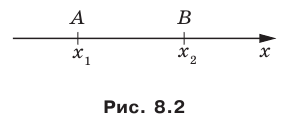
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
(left|ACright|=left|CBright|)
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
(left|ACright|=left|CBright|Leftrightarrowleft|x_C-x_Aright|=left|x_B-x_Cright|)
Опустим знак модуля и получим справедливость двух выражений:
(x_C-x_A=x_B-x_C)
(x_C-x_A=-left(x_B-x_Cright))
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
(x_C=frac{x_A+x_B}2)
Следствием второго равенства будет следующее утверждение:
(x_A=x_B)
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
(x_C=frac{x_A+x_B}2)
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
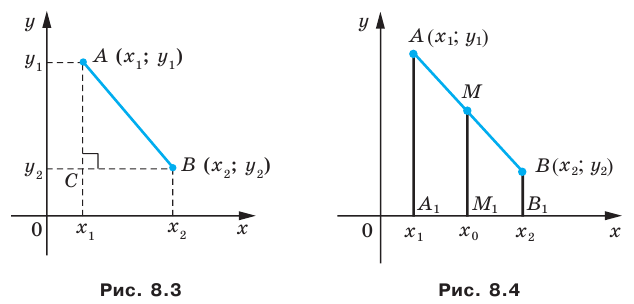
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
(A_xC_x=C_xB_x)
(A_yC_y=C_yB_y)
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
(x_C=frac{x_A+x_B}2)
(y_C=frac{y_A+y_B}2)
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2right))
Середина отрезка в пространстве
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz; Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
(left|A_xC_xright|=left|C_xB_xright|)
(left|A_yC_yright|=left|C_yB_yright|)
(left|A_zC_zright|=left|C_zB_zright|)
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2,;frac{z_A+z_B}2right))
Метод с использованием координат радиус-векторов концов отрезка
Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.
Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(xA,yA) и B(xB,yB), а также C, делящая пополам отрезок, ограниченный A и B.
По определению действий над вектором в геометрии:
((1);overrightarrow{OC}=frac12timesleft(overrightarrow{OA}+overrightarrow{OB}right))
В рассматриваемой ситуации в точке C пересекаются диагонали параллелограмма с основаниями: (overrightarrow{OA},;overrightarrow{OB}
).
Это значит, что С — это центр диагоналей.
Поскольку координаты радиус вектора совпадают с координатами точки, имеем: (overrightarrow{OA}=left(x_A,;y_Aright),;overrightarrow{OB}=left(x_B,;y_Bright)
).
Произведем подстановку в формулу (1):
(overrightarrow{OC}=frac12timesleft(overrightarrow{OA}+overrightarrow{OB}right)=left(frac{x_A+x_B}2,;frac{y_A+y_B}2right)
).
Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:
(left(frac{x_A+x_B}2,;frac{y_A+y_B}2right))
По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2,;frac{z_A+z_B}2right))
Примеры решения задач
Задача № 1
Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.
Решение:
Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:
(x_O=frac{x_A+x_B}2=frac{5+1}2=frac62=3)
(y_O=frac{y_A+y_B}2=frac{4+left(-2right)}2=frac{4-2}2=frac22=1)
Точка O имеет координаты (3,1).
Ответ: (3,1).
Задача № 2
Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.
Решение:
Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:
(x_М=frac{x_В+x_С}2=frac{-3+2}2=frac{-1}2=-0,5)
(y_М=frac{y_В+y_С}2=frac{1+4}2=frac52=2,5)
Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками:
(AM=sqrt{left(x_M-x_Aright)^2+left(y_M-y_Aright)^2}=sqrt{left(-0,5-7right)^2+left(-2,5-3right)^2}=sqrt{-7,5^2+left(-5,5right)^2}=sqrt{56,25+30,25}=sqrt{86,5}
).
Ответ: √86,5.

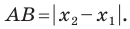
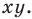
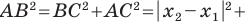
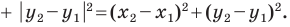

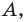
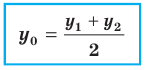
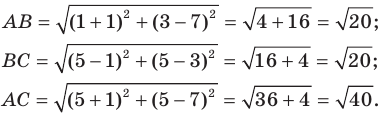

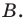
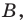
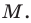
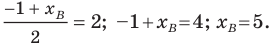
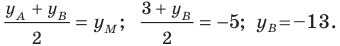
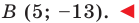
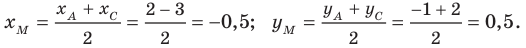
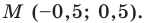
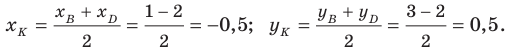
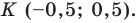
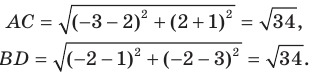

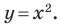
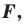 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;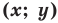 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре