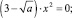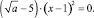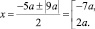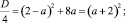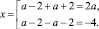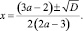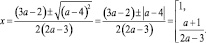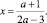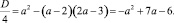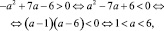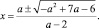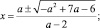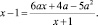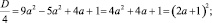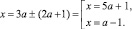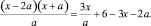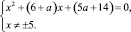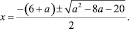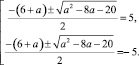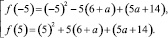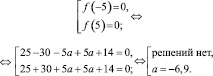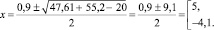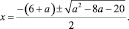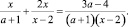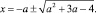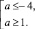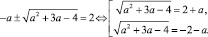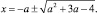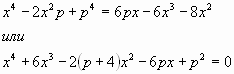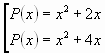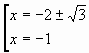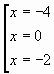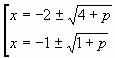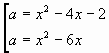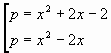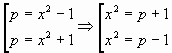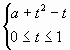К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.
Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:
у = kx, где x, y – переменные, k – параметр;
у = kx + b, где x, y – переменные, k и b – параметр;
аx2 + bх + с = 0, где x – переменные, а, b и с – параметр.
Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).
Задачи с параметром можно условно разделить на два типа:
а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.
б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.
Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.
Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:
1) -6a будет больше 3a, если а отрицательное число;
2) -6а = 3а в случае, когда а = 0;
3) -6а будет меньше, чем 3а, если а – число положительное 0.
Решение и будет являться ответом.
Линейные уравнения с параметром
Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.
При решении таких уравнений могут быть случаи:
1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.
2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.
3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.
Алгоритм решения такого типа уравнений:
1. Определить «контрольные» значения параметра.
2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
4. Записать ответ можно в следующем виде:
Ответ:
1) при … (значения параметра), уравнение имеет корни …;
2) при … (значения параметра), в уравнении корней нет.
Пример 1.
Решить уравнение с параметром |6 – x| = a.
Решение.
Легко видеть, что здесь a ≥ 0.
По правилу модуля 6 – x = ±a, выразим х:
x = 6 ± a.
Ответ: х = 6 ± a, где a ≥ 0.
Пример 2.
Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.
Решение.
Раскроем скобки: aх – а + 2х – 2 = 0
Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.
Ответ: х = 1 при а ≠ -2 и х € R при а = -2.
Пример 3.
Решить уравнение x/a + 1 = а + х относительно переменной х.
Решение.
Если а = 0, то преобразуем уравнение к виду а + х = а2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.
Если а ≠ 1, то последнее уравнение примет вид х = -а.
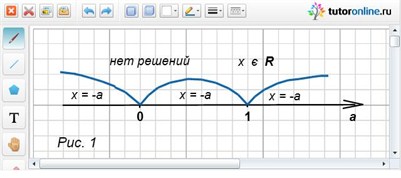
Данное решение можно проиллюстрировать на координатной прямой (рис. 1)
Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.
Графический метод
Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.
Пример 4.
Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?
Решение.
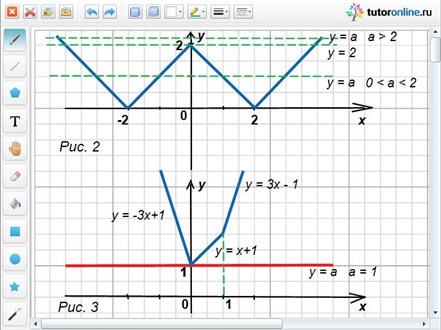
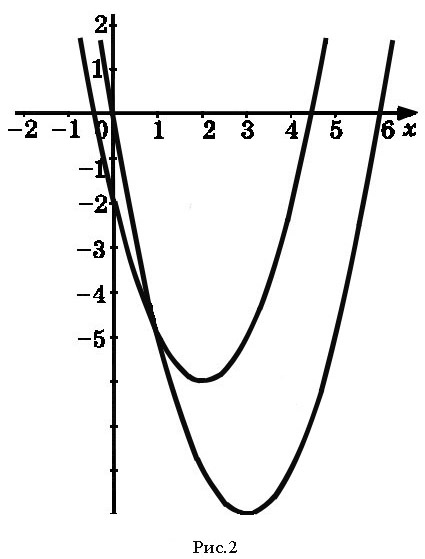
Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).
На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.
Ответ: корней у уравнения не будет, если а < 0; два корня будет в случае, если a > 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 < a < 2.
Пример 5.
При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?
Решение.
Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:
{-3x + 1, при x < 0,
y = {x + 1, при 0 ≤ x ≤ 1,
{3x – 1, при x > 1.
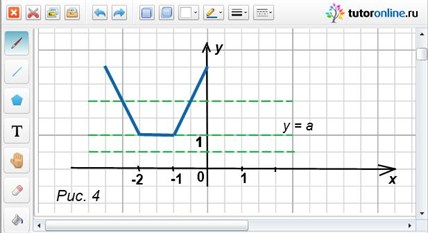
На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.
Ответ: а = 1.
Пример 6.
Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?
Решение.
График функции y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4).
Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.
Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Методика обучения решению квадратных уравнений с параметром
Разделы: Математика
Решение задач с параметром вызывает затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках недостаточно.
Цели разработки темы
- формирование устойчивого интереса к познавательному процессу при изучении математики и оценка возможности овладения предметом с точки зрения дальнейшей перспективы;
- обеспечение прочного и сознательного усвоения учащимися системой математических знаний, умений и навыков;
- формирование качества мышления, характерного для математической деятельности и необходимые человеку для жизни в современном обществе;
- выявление и развитие математических способностей учащихся.
- Задачи разработки темы:
- показать универсальные алгоритмы для решения квадратных уравнений с параметром;
- научить приемам решения различного класса задач с параметром, способствовать овладению технических и интеллектуальных математических умений на уровне свободного их использования;
- использование новых современных педагогических технологий обучения.
В математике параметр – это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи (“параметр” с греческого “parametron” – отмеривающий)..
Если ставится задача для каждого значения параметра а из некоторого числового множества А решить уравнение F(х;а)= 0 относительно х, то это уравнение называют уравнением с переменной х и параметром а, а множество А – областью изменения параметра. Под областью определения уравнения F(х;а)=0 с параметром а понимаются такие системы значений х и а, при которых F(х;а) имеет смысл. Все значения параметра а, при которых F(х;а) не имеет смысла, включать в число значений параметра, при которых уравнение не имеет решений. Под областью изменения параметра (если не сделано специальных оговорок) берется множество всех действительных чисел, а задачу решения уравнения с параметром формулировать следующим образом: решить уравнение F(х;а)=0 (с переменной х и параметром а) – это значит на множестве действительных чисел решить семейство уравнений, получающихся из данного уравнения при всех действительных значениях параметра или установить, что решений нет.
В связи с тем, что выписать каждое уравнение из бесконечного семейства уравнений невозможно, но каждое уравнение семейства должно быть решено, следовательно, необходимо по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств. Для разбиения множества значений параметра на подмножества, удобно пользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра называются контрольными.
1. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ
Задачи с параметрами можно разделить на два больших класса:
- задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение;
- задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям.
В зависимости от типа задачи изменяется и вид ответа. В первом случае в решении и ответе должны быть рассмотрены все возможные значения параметров. Если хотя бы одно значение какого-либо параметра не исследовано, решение задачи не может быть признано полным.
Во втором случае в ответе перечисляются только те значения параметра, при которых выполнены условия задачи, а при решении подобных задач обычно решать заданное уравнение нет необходимости.
Уравнение вида Ах 2 + Вх + С= 0 , где А, В, С — выражения, зависимые от параметра, х – переменная — называется квадратным уравнением с параметром.
Уравнение вида ах 2 +вх+с=0, где 
В зависимости от значения дискриминанта возможны три случая:
D > 0. Данное квадратное уравнение имеет два действительных корня
D=0. Данное уравнение имеет корень двойной кратности 
D 2 +2кх+с=0 со вторым коэффициентом (в=2к) четным, для нахождения корней удобно пользоваться формулами: 

№ 1.1. Определите все значения параметра а при которых уравнение ах 2 +2(а+1)х+а+3=0 имеет два неравных корня.
Если а=0, то имеем 0·х 2 +2(0+1)х+0+3=0, 2х+3=0 — данное уравнение является линейным, х=-1,5 – единственный корень. Итак, а=0 не удовлетворяет условию задачи.
Если а?0, то уравнение имеет два различных корня, когда дискриминант 
Найдем
Если а=0, то имеем 2·0·х 2 -4(0+1)х+4·0+1=0, -4х+1=0 — данное уравнение является линейным, х=0,25 – единственный корень. Итак, а=0 удовлетворяет условию задачи.
Если а 


С учетом а=0, запишем ответ: а=-0,5, а=0, а=2.
№ 1.3. При каких значениях параметра а квадратное уравнение (5а-1)х 2 -(5а+2)х+3а-2=0 не имеет корней?
Если 5а-1=0,а=0,2, то имеем (5*0,2-1)х 2 -(5*0,2+2)х+3*0,2-2=0,
-3х-1,4=0 — данное уравнение является линейным, х = 
Итак, а=0,2 не удовлетворяет условию задачи.
Если а 



№ 1.4. Определите все значения параметра а при которых уравнение (2а-1)х 2 +ах+2а-3=0 имеет не более одного решения.
Если 2а-1=0,а=0,5, то имеем (2·0,5-1)х 2 +0,5·х+2·0,5-3=0, 0,5х-2=0 — данное уравнение является линейным, х=4 — единственный корень.
Итак, а=0,5 удовлетворяет условию задачи.
Если а 

Найдем D=а 2 -4(2a-1)(2а-3)=-15a 2 +32a-12, -15a 2 +32a-12
15a 2 -32a+12?0, а1=




С учетом а 

С учетом а=0,5, запишем ответ: 
2. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ.
Квадратное уравнение ах 2 +вх+с=0, где а 
Общая схема решения неполных квадратных уравнений с параметрами.
ах 2 =0, где а 

Следовательно, уравнение имеет два совпадающих корня, равных нулю.
Если а=0, то х — любое действительное число.
ах 2 +с=0, где а









№ 2.1. При каких значениях параметра а оба корня уравнения 2х 2 +(3а 2 -|а|)х-а 2 -3а=0 равны нулю?
Оба корня квадратного уравнения равны нулю, когда
№ 2.2. При каких значениях параметра а, корни уравнения 2 х 2 -(5а-3)х+1=0 равны по модулю, но противоположны по знаку?
Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда 5а-3=0,а=0,6, но с учетом того, что имеем уравнение 2х 2 +1=0, х 2 =-0,5, которое корней не имеет. Ответ: 
№ 2.3. При каких значениях параметра а один из двух различных корней уравнения 3х 2 +х+2а-3=0 равен нулю?
Параметр должен удовлетворять условию: 2а-3=0, а=1,5. Ответ: а=1,5.
№ 2.4. При каких значениях параметра а корни уравнения 3х 2 +(а 2 -4а)х+а-1=0 равны по модулю, но противоположны по знаку?
Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда:

№ 2.5. Решить относительно х неполное квадратное уравнение х 2 -2а+1=а.
х 2 =а+2а-1; х 2 =3а-1.
Если 3а-1=0, а= 
Если 3а-1 0. а>

Ответ: при а

3. ИССЛЕДОВАНИЕ И РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ.
№ 3.1. Исследовать и решить уравнение с параметром х 2 –2(а-1)х+2а+1=0.
Найдем дискриминант: 




1) При а-1=0, а=1 имеем линейное уравнение 4х-1=0, х=
2) При а 
D1 = (а+1) 2 -(а–1)(2а-2)=а 2 +2а+1-а 2 +2а+а-2=5а-1.
D1>0. 5а-1>0, а>


D1=0. 5а-1=0, а=

х 2 +2х-8–ах+4а=0; х 2 +(2-а)х+4а-8=0. Уравнение является квадратным.
Найдем дискриминант: D=(2-а) 2 -4(4а-8)=4-4а+а 2 -16а+32= а 2 -20а+36.
D>0. а 2 20а+36>0, (а-18)(а -2)>0, а 18, то уравнение имеет два действительных корня 
D=0. (а-18)(а-2)=0, а=2, то 

D 2 равен 1, то уравнение принимает вид х 2 +px+q, где p и q — некоторые числа называется приведенным квадратным уравнением.
Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
ах 2 +вх+с=0, где х1 и х2 – корни квадратного уравнения, то
Справедливо утверждение, обратное теореме Виета.
Теорема: Если числа p и q таковы, что их сумма равна -p, а произведение равно q. то эти числа являются корнями уравнения х 2 +px+q=0.
№ 4.1. При каком значении параметра а сумма обратных величин действительных корней уравнения 2х 2 -2ах+а 2 -2=0 равна 
Пусть х1 и х2 – корни квадратного уравнения, по условию 
По теореме Виета: 
Найдем дискриминант квадратного уравнения:
Имеем: 
№ 4.2. В уравнении (а 2 -5а+3)х 2 +(3а-1)х+2=0 определите а так, чтобы один из корней был вдвое больше другого.
Пусть х1 и х2 – корни квадратного уравнения, по условию х1 =2 х2. Заметим, что кратное сравнение выполняется только для положительных чисел.
По теореме Виета и условию задачи имеем систему:
Составим и решим уравнение:
Можно вычислить дискриминант данного уравнения, а затем проверить, удовлетворяет ли данное значение параметра а условию, что дискриминант неотрицателен, а так же, что корни положительны. Однако в данной задаче значительно проще сделать проверку, подставив это значение а в исходное уравнение.
При 
№ 4.3. Найти все значения параметра а, при которых квадратное уравнение (а+2)х 2 –ах-а=0 имеет два корня, расположенных на числовой прямой симметрично относительно точки х=1.
При а+2=0, а=-2, то 2х+2=0, х=-1 – единственное решение, следовательно данное значение а не удовлетворяет условию задачи.
При а
По теореме Виета имеем:
Решим первое уравнение системы: 2(а+2)=а, а=-4.
Найдем дискриминант данного квадратного уравнения:
Данное значение а=-4 удовлетворяет полученным значениям. Ответ: а=-4.
Ответ: при а = — 4.
- ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
- Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Минск; “Аверсэв”. 2005.
- Амелькин В. В., Рабцевич В. Л. Задачи с параметрами. Минск; “Асар”. 1996.
- Данкова И. Н., Бондаренко Т. Е., Емелина Л. Л., Плетнева О. К.Предпрофильная подготовка учащихся 9 классов по математике. Москва; “5 за знания”.2006.
- Литвиненко В. Н., Мордкович А. Г.. Практикум по элементарной математике. Москва; “Просвещение”.1991.
- Родионов Е. М. Решение задач с параметрами. Москва; “Русь – 90”. 1995.
- Студенецкая В. Н., Сагателова Л. С. Математика 8 – 9классы: сборник элективных курсов. Волгоград; “Учитель”. 2006.
- Шарыгин И. Ф. Решение задач. Москва; “Просвещение”. 1994.
- Шахмейстер А. Х. Уравнения и неравенства с параметрами. Санкт-Петербург; “Петроглиф”. 2006.
Контрольное значение в уравнении с параметром
решение ЗАДАЧ С ПАРАМЕТРАМИ
Глава І
Глава ІІ
Факультативные занятия
Понятие о параметрах. Контрольные значения параметра. Постановка задач с параметрами
Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|=a–1 не следует неотрицательность значений выражения a–1, и если a–1
Что означает «решить задачу с параметром»?
Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
Решение уравнений с параметрами
Решение уравнений с параметрами
Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами.
В этом уравнении х – неизвестное, a, b,c – коэффициенты, которые могут принимать различные числовые значения. Заданные таким образом коэффициенты называются параметрами.
Одно уравнение с параметрами задает множество уравнений (для всех возможных значений параметров).
–102–1000y=
это все уравнения, которые задает уравнение с параметрами ax+b=c.
Решить уравнение с параметрами – это значит:
1. Указать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров.
2. Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение определяет корень уравнения.
Обратимся к уже приведенному уравнению с параметрами ax+b=c и решим его.
Если а¹0, то 
Если а=0, то получаем b=c, если это действительно так, то корнем уравнения является любое действительное число, если же b¹c, то уравнение решений не имеет.
Таким образом, мы получили:
при а¹0, 
при а=0 и b=c, х – любое действительное число;
при а=0 и b¹c, уравнение корней не имеет.
В процессе решения этого уравнения мы выделили значение параметра а=0, при котором происходит качественное изменение уравнения, такое значение параметра мы в дальнейшем будем называть «контрольным». В зависимости от того, какое уравнение мы имеем, «контрольные» значения параметра находятся по-разному. Рассмотрим различные типы уравнений и укажем способ нахождения «контрольных»значений параметра.
I. Линейные уравнения с параметром и уравнения, приводимые к линейным
В таких уравнениях «контрольными» значениями параметров, как правило, являются значения, обращающие в нуль коэффициенты при х.
Пример 1. Решить уравнение с параметром: 2а(а–2)х=а–2
1. «Контрольными» значениями являются значения, удовлетворяющие условию:
решим это уравнение относительно переменной а.
2. Решим первоначальное уравнение при «контрольных» значениях параметра.
При а=0 имеем 0×х=–2, но это не имеет место ни при каких действительных значениях х, то есть в этом случае уравнение корней не имеет.
При а=2 имеем 0×х=0, это справедливо при любом значении х, значит, корнем уравнения является любое действительное число х.
3. Решим первоначальное уравнение, в случае, когда а¹0 и а¹2, тогда 2а(а–2)¹0 и обе части уравнения можно поделить на 2а(а–2), получим:


Ответ: при а=0, корней нет;
при а=2, корень – любое действительное число;
при а¹0, а¹2, 
Можно представить алгоритм решения такого типа уравнений.
1. Определить «контрольные» значения параметра.
2. Решить уравнение относительно х, при контрольных значениях параметра.
3. Решить уравнение относительно х, при значениях, отличных от «контрольных».
4. Записать ответ в виде:
Ответ: 1) при значениях параметра. , уравнение имеет корни. ;
2) при значениях параметра. , уравнение имеет корни. ;
3) при значениях параметра. , уравнение корней не имеет.
Пример 2. Решить уравнение с параметром
1. Найдем контрольные значения параметра
2. Решим уравнение при а=1
0×х=(1+2×1–3) Û 0×х=0 Þ х – любое действительное число.
3. Решим уравнение при а¹1
а2–2а+1¹0 Þ
разложим числитель и знаменатель дроби на множители
так как а¹1, дробь можно сократить
4. Ответ: 1) при а=1, х – любое действительное;
2) при а¹1, 
Пример 3. Решить уравнение с параметром
1. Так как параметр а стоит в знаменателе, то а обязательно должно быть отлично от нуля. При а¹0 приведем это уравнение к стандартному виду линейного уравнения, для чего обе части умножим на а.
найдем «контрольные» значения а
2. Решим уравнение при а=2
это равенство не имеет места ни при каких значениях х.
3. Решим уравнение при а¹2
2–а¹0 Þ 
4. Ответ: 1) при а=2, корней нет;
2) при а¹0, а¹2, 
3) при а=0 уравнение не имеет смысла.
Пример 4. Решить уравнение с параметром
1. Так как параметр а стоит в знаменателе дроби, то чтобы уравнение имело смысл, а+2 обязательно должно быть отлично от нуля
так как х стоит в знаменателе дроби, то х¹0. Преобразуем уравнение
так как х¹0 и а¹–2, уравнение равносильно уравнению
найдем контрольные значения параметра
2. Решим уравнение при а=–3.
при любом х равенство места не имеет
так как х¹0, то проверим, нет ли значений а, при которых х=0, для этого приравняем полученную дробь к нулю


поэтому, чтобы уравнение имело смысл 
4. Ответ: 1) при а=–3, а=–2, 
2) при а¹–2, а¹–3, 

II. Квадратные уравнения с параметром и уравнения, приводимые к квадратным
В таких уравнениях в качестве «контрольных» берут обычно значения параметра, обращающие в нуль коэффициент при х2, так как в этом случае уравнение становится линейным, а также значение параметра, обращающие в нуль дискриминант уравнения, так как от значения дискриминанта зависит число действительных корней квадратного уравнения.
Пример 5. Решить уравнение с параметром
1. Найдем значения параметра, обращающие в нуль коэффициент при х
2. Решим уравнение при а=1
0×х2+2(2×1+1)х+4×1+3=0 Û 6х+7=0 Û 
3. Найдем значения параметра, обращающие в нуль дискриминант уравнения
4(5а+4)=0 Û 
4. Решим уравнение при 


9х2+6х+1=0 Û (3х+1)2=0 Û 
5. Решим уравнение при а¹1, 
7. Записать ответ.
Пример 6. Решить уравнение с параметром
1. Так как а стоит в знаменателе дроби, то уравнение имеет смысл только при а¹0. В знаменателе стоят и выражения а2х–2а и 2–ах, которые тоже должны быть отличны от нуля
а2х–2а¹0 Û а(ах–2)¹0 Û а¹0, ах–2¹0 Û а¹0, 
2–ах¹0 Û 
Таким образом, мы видим, что 
2. Решим уравнение при а¹0,


3. Найдем значения параметра, обращающие в нуль коэффициент при х2
4. Решим уравнение (*) при а=1
сразу проверим, не совпадает ли х с
а=1 Þ 
5. Найдем значение параметра, обращающего в нуль дискриминант уравнения (*)
но при этом значении параметра уравнение не имеет смысла.
Замечаем, что так как D=4а2>0 при любом значении а¹0, поэтому уравнение (*) имеет два действительных корня при а¹1, найдем их


Проверим, чтобы

Найдем чему равен х2 при а=–2



6. Ответ: 1) а=0 уравнение не имеет смысла;
3) а¹0, а¹–2, 
4) а=–2, 
Пример 7. При каких значениях р корни уравнения х2+6х+р+3=0 будут отрицательными?
1. Квадратное уравнение имеет действительные корни при условии D³0.
Найдем дискриминант этого уравнения и найдем значения параметра, удовлетворяющие этому условию
2. При p£6 корни квадратного уравнения вычисляются по формулам
3. Найдем значения р, для которых х1
http://sites.google.com/site/reseniezadacsparametrami/ponatie-o-parametrah-kontrolnye-znacenia-parametra-postanovka-zadac-s-parametrami
http://pandia.ru/text/80/014/39350.php
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Романова Т.Е.
1
Романов П.Ю.
1
1 ФГБОУ ВО «Магнитогорский государственный технический университет им. Г.И. Носова»
В статье предпринята попытка реализовать теорию поэтапного формирования умственных действий в процессе обучения школьников решению задач с параметрами. На основе разработанной авторами системы задач предлагается методика построения ориентировочной основы решения параметрических задач. Предлагаемая последовательность задач, составленная с учетом сформулированных авторами требований, способствует активному участию школьников в построении ориентировочной основы решения задач данного типа. Разнообразные задачи позволяют корректировать и совершенствовать ориентировочную основу в зависимости от сложности квадратных уравнений с параметрами и уравнений, к ним сводимым. При этом создаваемые учащимися приемы поиска контрольных значений параметров, включенные в ориентировочную основу действий, позволяют избежать громоздких математических вычислений, формируя исследовательские умения школьников и подготавливая их к осуществлению исследовательской деятельности.
задачи с параметрами
ориентировочная основа деятельности
контрольные значения параметра
1. Романов П.Ю. Технология воспитания педагога-исследователя в системе непрерывного образования // Научные труды МПГУ. Серия: Естественные науки. – 2001. – С. 290–294.
2. Романов П.Ю., Романова Т.Е. Решение задач с параметрами // Математика. Первое сентября. – 2001. – № 12. – С. 13–15.
3. Романов П.Ю., Романова Т.Е. Роль графической интерпретации результатов решения задач с параметрами в организации исследовательской деятельности учащихся // Современные проблемы обучения математике в школе / ред. Е.И. Жилина. – Магнитогорск, 2000. – С. 84–90.
4. Романов П.Ю., Романова Т.Е. Системный подход в обучении учащихся написанию уравнения касательной к графику функции // Систематизация и обобщения при обучении школьников математике / под ред. Е.И. Жилиной. – Магнитогорск, 1998. – С. 36–41.
5. Романова Т.Е. Исследование систем линейных уравнений с двумя неизвестными и параметром // Педагогические аспекты математического образования / под ред. П.Ю. Романова. – Магнитогорск, 2011. – С. 112–117.
6. Романова Т.Е. Решение уравнений и неравенств первой степени. Уравнения и неравенства, содержащие переменную под знаком модуля: учебное пособие. – Магнитогорск, 2004. – 63 с.
Задачи с параметрами уверенно вошли в материалы государственной итоговой аттестации и единого государственного экзамена по математике. Их решение вызывает немалые трудности у учащихся, которые могут быть объяснены отсутствием в ныне действующих учебниках четких методических указаний по решению задач данного класса.
Психологов всегда интересовал процесс усвоения знаний и умений учащимися. Как правильно организовать работу по усвоению знаний и умений учащимися? Ответить на этот вопрос позволила теория поэтапного формирования умственных действий П.Я. Гальперина.
Классно-урочная форма обучения, на наш взгляд, позволяет организовывать следующие этапы данной теории: ориентировка школьников в материале и способах работы с ним; осуществление пошагового контроля за усвоением каждого действия каждым школьником в ходе решения задачи; переход от пошагового контроля школьников к их самоконтролю [4].
Приведем примеры разработанных нами систем заданий по теме «Квадратные уравнения с параметрами» [2]. При их составлении мы руководствовались тем, что:
– число задач, входящих в систему, должно быть достаточным для организации каждого из этапов теории;
– сложность задач в системе должна нарастать постепенно;
– последовательность задач должна способствовать активному участию школьников в моделировании ориентировочной основы формируемого действия.
Изучение данной темы необходимо начать с рассмотрения неполных квадратных уравнений с параметрами.
Задание 1. При всех значениях параметра а решить уравнения:
1) ax2 = 0;
2) (a – 2)(x – 1)2 = 0;
3)
4)
Далее переходим к решению приведенных квадратных уравнений, числовое значение дискриминанта которых представляет собой квадрат целого числа.
Задание 2. При всех значениях параметра а решить уравнение
x2 + 5ax = 14a2.
x2 + 5ax – 14a2 = 0; D = 25a2 + 56a2 = 81a2;
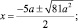
Ответ: при всех действительных значениях параметра а уравнение имеет корни x = –7a и x = 2a.
Задание 3. При всех значениях параметра а решить уравнения:
1) x2 = –6ax – 8a2;
2) x2 – 18a2 = 3ax;
3) x2 + 8ax + 7a2 = 0;
4) x2 – 15a2 = 2ax.
Следующим этапом решения квадратных уравнений с параметром является решение уравнений, дискриминант которых есть полный квадрат некоторого двучлена.
Задание 4. При всех значениях параметра а решить уравнение
x2 + (4 – 2a)x = 8a.
x2 + (4 – 2a)x – 8a = 0;
x2 + 2(2 – a)x – 8a = 0;
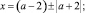
Ответ: при всех действительных значениях параметра а уравнение имеет корни x = 2a и x = –4.
Решение вышепредставленных уравнений позволяет составить ориентировочную основу действий (ООД) для решения квадратных уравнений с параметрами данного типа.
ООД решения квадратных уравнений с параметрами
• Привести уравнение к стандартному виду.
• Найти дискриминант квадратного уравнения.
• Найти контрольное значение параметра, исследуя дискриминант.
• Найти корни уравнения при контрольном значении параметра.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Развертка по параметру позволяет систематизировать, обобщить и интерпретировать полученные результаты [3]. Далее учащиеся должны познакомиться с новым для них приемом решения квадратных уравнений – понижения степени. Овладевая им, учащиеся начинают понимать, что при определенных значениях параметра, квадратное уравнение приобретает статус линейного, решение которых учащимся известно [5, 6].
Задание 5. При всех значениях параметра а решить уравнение
(2a – 3)x2 + a + 1 = (3a – 2)x.
Для решения данного уравнения воспользуемся приемом понижения степени. Приравняем к нулю коэффициент при x2 и найдем значение параметра а, при котором квадратное уравнение превращается в линейное:
2a – 3 = 0; a = 1,5.
При a = 1,5 исходное уравнение принимает вид
–(3•1,5 – 2)x + 1,5 + 1 = 0,
откуда x = 1.
Найдем корни уравнения
(2a – 3)x2 – (3a – 2)x + a + 1 = 0
для всех a — 0:
D = (3a – 2)2 – 4(2a – 3)(a + 1);
D = a2 – 8a + 16; D = (a – 4)2;
Анализируя значения дискриминанта, получаем контрольное значение параметра a = 4. Для a = 4 исходное уравнение имеет корень четной кратности x = 1.
Если a ≠ 1,5 и a≠ 4, то
Ответ: a = 1,5; a = 4: x = 1;
a ≠ 1,5 a ≠ 4: x = 1,
Если при решении задания 5 дискриминант представлял собой полный квадрат двучлена, то уравнение задания 6 не обладает данным преимуществом. Поэтому при его решении необходимо провести полное исследование дискриминанта (квадратного трехчлена).
Задание 6. При всех значениях параметра а решить уравнение
(a – 2)x2 – 2ax = 3 – 2a.
Преобразуем уравнение к стандартному виду
(a – 2)x2 – 2ax + 2a – 3 = 0
и применим к нему прием понижения степени.
Если a – 2 = 0, то a = 2, и уравнение принимает вид –4x + 1 = 0, откуда x = 0,25.
Если a ≠ 2, то
Исследуем дискриминант:
1. Если
то уравнение имеет два корня. Получили два новых контрольных значения параметра а: и
Если a = 1, то уравнение принимает вид
x2 + 2x + 1 = 0,
откуда x = –1.
Если a = 6, то уравнение принимает вид
4×2 – 12x + 5 = 0,
откуда x = 1,5.
Если 1 < a < 6, то
2. Если
(a – 1)(a – 6) > 0,
то уравнение не имеет корней.
Ответы: a = 1: x = –1; a = 2: x = 0,25;
a = 6: x = 1,5;
1 < a < 2 и 2 < a < 6:
a < 1 и a > 6: решений нет.
Овладение новым приемом решения квадратных уравнений ставит вопрос о корректировке ООД решения квадратных уравнений с параметрами.
ООД решения квадратных уравнений с параметрами
• Привести уравнение к стандартному виду.
• Найти контрольные значения параметра, используя прием понижения степени уравнения.
• Найти корни уравнения при этом значении параметра.
• Найти дискриминант квадратного уравнения.
• Найти контрольное значение параметра, исследуя дискриминант.
• Найти корни уравнения при новых контрольных значениях параметра.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Усвоить ориентировочную основу решения полных квадратных уравнений с параметрами можно при помощи уравнений задания 7.
Задание 7. При всех значениях параметра а решить уравнения:
1) ax2 + (a + 1)x + 1 = 0;
2) (a – 1)x2 + 1 = 2x + a;
3) (b – 2)x2 + 3b +2 = 4bx;
4) ax2 = (a + 1)x + 1 + 2a.
Далее переходим к рассмотрению дробно-рациональных уравнений с параметрами, решение которых сводится к решению квадратных уравнений. При решении уравнений данного вида необходимо с самого начала указывать значения параметра и переменной, при которых уравнение имеет смысл. Знание области допустимых значений переменной и параметра позволяет в дальнейшем исследовать корни уравнения.
Изучение дробно-рациональных уравнений начинаем с уравнений, числитель которых представляет собой квадратный трехчлен в самом «хорошем случае» – его дискриминант является полным квадратом.
Задание 8. При всех значениях параметра а решить уравнение
Укажем область допустимых значений переменной х: x ≠ –1.
Преобразуем уравнение к стандартному виду
x2 – 6ax + 5a2 – 4a – 1 = 0
и найдем его корни:
Найденные корни должны быть отличны от нуля, то есть 5a + 1 ≠–1 или a – 1 ≠ –1. Откуда a ≠ –0,4, a ≠ 0.
Найденные значения параметра а представляют собой его контрольные значения. При них исходное уравнение имеет один корень x = 1 или x = –1,4.
Ответ:
a ≠ –0,4: x = –1,4;
a ≠ 0: x = 1;
a ≠ –0,4, a ≠ 0: x = 5a + 1; x = a – 1.
Задание 9. При всех значениях параметра а решить уравнение
Решение данного уравнения требует ограничений на параметр: a ≠ 0. При этом условии исходное уравнение равносильно уравнению
x2 – (2a – 3)x – 6a = 0.
Решая его, находим, что x = 3 или x = –2a. Записываем ответ.
Ответ:
a = 0: решений нет;
a ≠ 0: x = 3; x = –2a.
Далее знакомим учащихся с решением дробно-рациональных уравнений, решение которых сводится к квадратному уравнению с дискриминантом, не являющимся полным квадратом. Учащиеся понимают, что в этом случае корень из дискриминанта не извлекается, и они сталкиваются с необходимостью решать иррациональные уравнения, что довольно трудоемко, особенно для детей, которые по возрастным показателям еще не владеют техникой их решения. В этом случае на помощь может прийти прием, ведущий к цели более коротким и технически простым путем.
Задание 10. При всех значениях параметра а решить уравнение
Запишем ограничения на значения переменной x: x ≠ ±5. После необходимых преобразований, перейдем к системе, равносильной исходному уравнению:
Дискриминант квадратного трехчлена, стоящего в левой части уравнения, равен
D = 36 + 12a + a2 – 4(5a + 14) = a2 – 8a – 20.
Так что для того, чтобы уравнение имело корни, необходимо, чтобы a2 – 8a – 20 ≠ 0. Последнее неравенство выполняется для a ≠ –2 или a ≠ 10.
При остальных значениях параметра а квадратное уравнение решений не имеет и, тем более, не имеет решений исходное уравнение.
Итак, при a ≠ –2 или a ≠ 10 квадратное уравнение имеет два корня
Исключим посторонние корни. Для этого найдем значения параметра а, при которых х будет равняться 5 или –5:
Выполнение данных условий требует решения четырех иррациональных уравнений.
Выйти из затруднительного положения позволяет следующее рассуждение: каждое значение параметра задает свое, соответствующее только этому значению параметру, уравнение. Естественно, что каждое уравнение, в свою очередь, предполагает свой «набор» корней. Значит, справедливо и обратное: определенному значению переменной х соответствует «свое» значение параметра а.
Поэтому вычислим значения квадратного трехчлена в «запрещенных» точках:
Тогда
Итак, если a = –6,9, то
Но x = 5 не является корнем, следовательно, остается корень x = –4,1.
Для завершения решения, найдем корни уравнения в контрольных точках a = –2 и a = 10: если a = –2, то x = –2; если a = 10, то x = –8.
Ответ:
a = –6,9: x = –4,1;
a = –2: x = –2;
a = 10: x = –8;
–2 < a < 10: решений нет;
a < –6,9; –6,9 < a < –2; a > 10:
В свете рассмотренных дробно-рациональных уравнений с параметрами внесем дополнения в ориентировочную основу решения уравнений, сводимых к квадратным.
ООД решения дробно-рациональных уравнений с параметрами
• Найти области допустимых значений переменной и параметра.
• Привести уравнение к стандартному виду.
• Найти контрольное значение параметра, используя прием понижения степени уравнения.
• Найти корни уравнения при этом значении параметра.
• Найти дискриминант квадратного уравнения.
• Найти контрольные значения параметра, исследуя дискриминант.
• Найти корни уравнения при новых контрольных значениях параметра.
• Найти контрольные значения параметра по области допустимых значений переменной, используя прием подстановки «запрещенных» значений переменной в формулу корней квадратного уравнения.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Составленная ориентировочная основа решения квадратных уравнений и уравнений, к ним сводимых, позволяет выделить приемы нахождения контрольных значений параметра, от знания которых зависит решение уравнения:
1. Нахождение области допустимых значений параметра.
2. Использование приема понижения степени уравнения.
3. Исследование дискриминанта.
4. Исключение посторонних корней уравнения по области допустимых значений переменной (прием подстановки «запрещенных» значений переменной в формулу корней квадратного уравнения).
Рассмотрим решение дробно-рационального уравнения с параметром, сводимого к квадратному, которое сочетает в себе использование всех выделенных приемов нахождения контрольных значений параметра.
Задание 11. При всех значениях параметра а решить уравнение
Областью допустимых значений переменной являются все x ≠ 2, параметра – все a ≠ –1.
При a = –1 уравнение не имеет смысла, а значит, не имеет решений.
Преобразуем уравнение к виду
x2 + 2ax + 4 – 3a = 0
и найдем его корни, отличные от 2. Дискриминант квадратного трехчлена, стоящего в левой части уравнения, равен
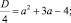
Естественно, для того чтобы уравнение имело решения, дискриминант должен быть неотрицательным:
a2 + 3a – 4 ≥ 0,
откуда
Получили новые контрольные значения параметра а: a = –4 и a = 1.
Если a = –4, то x = 4. Если a = 1, то x = –1.
Составим уравнение, позволяющее найти те значения параметра а, при которых переменная х принимает значение 2:
Видим, что для нахождения контрольных значений параметра а, при которых корни уравнения принимают статус «запрещенных», необходимо решить два иррациональных уравнения. Чтобы избежать этого, воспользуемся рассмотренным выше приемом и найдем новые контрольные значения параметра а, подставив в уравнение
x2 + 2ax + 4 – 3a = 0,
«запрещенные» значения переменной x:
22 + 2a•2 + 4 – 3a = 0,
откуда a = –8. Систематизируем полученные решения и запишем ответ.
Ответ:
a = –8: x = 14;
a = –4: x = 4;
a = 1: x = –1;
–4 < a < 1, a ≠ –1: решений нет;
a ≠ –8, –4 < a, a > 1:
Предлагаемая методика построения ООД позволяет обучить школьников решению целого класса задач с параметрами, а совместное выделение приема нахождения контрольных значений готовит учащихся к осуществлению исследовательской деятельности, освоению профессионально значимых умений [1].
Библиографическая ссылка
Романова Т.Е., Романов П.Ю. ИСПОЛЬЗОВАНИЕ ПРИЕМОВ НАХОЖДЕНИЯ КОНТРОЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРИ ПОСТРОЕНИИ ОРИЕНТИРОВОЧНОЙ ОСНОВЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ // Современные наукоемкие технологии. – 2016. – № 12-1.
– С. 186-191;
URL: https://top-technologies.ru/ru/article/view?id=36499 (дата обращения: 27.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Уравнениями с параметром называются уравнения,
у которых коэффициенты заданы не конкретными
числовыми значениями, а обозначены буквами.
Решить уравнение с параметром – это значит:
а) исследовать, при каких значениях параметров
уравнение имеет корни и при каких не имеет;
б) выяснить количество корней при различных
значениях параметров;
в) найти все выражения для корней.
Уравнения с параметром весьма различны по
структуре:
Моя работа посвящена отысканию метода решения
уравнений с параметрами вида
F(xn; p2) =0
В основе этого метода лежит взгляд на параметр,
как на переменную, т.е. уравнение F(xn;p?)=0
можно рассматривать как квадратное относительно
параметра р.
Задача 1. Пусть нужно решить уравнение с
параметром
Преобразуем данное уравнение
Это уравнение 4-й степени относительно х, причём
содержит и
. Как его решить?
Но заметим, что это уравнение является
квадратным относительно , т.е. вида
. Применим наш метод:
1. Перепишем уравнение в виде
, т.е.
рассмотрим его как квадратное относительно .
2. Найдем корни уравнения по формуле корней
квадратного уравнения:
3. Далее используем графический метод. В системе
координат
построим параболы ,
и
,
4. Найдём точки пересечения графиков функций.
Для этого приравняем
, отсюда
, т.е. точка
пересечения единственная .
5. По рисунку видно, что горизонтальная прямая
не имеет общих точек с параболами, если она
проходит ниже , т.е.
при данное
уравнение не имеет корней
при
уравнение имеет единственный корень
при
уравнение имеет два корня т.к. прямая имеет две точки
пересечения с параболой , отсюда
,
,
при и
— три корня
при
при
при и
уравнение
имеет четыре корня
Этот метод не является универсальным, но во
многих случаях является весьма результативным и
позволяет решать уравнения повышенной
сложности, второй степени и выше.
Задача 2. Определить число корней уравнения
в зависимости от параметра а х4-10х3-2(а-11)х2+2(5а
+ 6)х +2а + а2 =0 (1)
Решение. Уравнение является квадратным
относительно параметра а. Перепишем (1) в виде (2)
Найдём дискриминант
Решая уравнение (2), находим
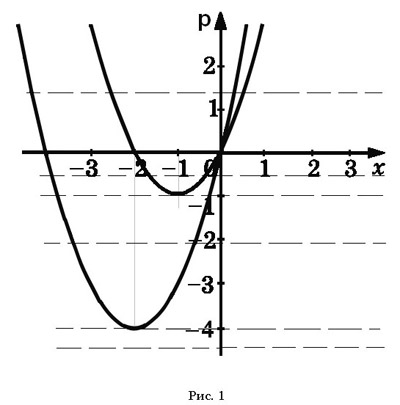
Построим в системе координат (х; а) графики
функций
и (рис 2)
Найдем точки пересечения графиков функций. Для
этого приравняем отсюда
. Далее рассуждая аналогично, как и в
задаче 1, получим
Ответ: если , уравнение корней не имеет;
если один
корень;
если ,
уравнение имеет два корня;
если три
корня;
если —
четыре корня.
Задача 3. Найти все значения параметра р,
при которых уравнение (3)
имеет ровно три решения.
Решении. Уравнение (3) является квадратным
относительно р. Перепишем его в виде
Найдем корни уравнения
В системе координат (х; р) построим параболы
и
(рис.2)
Данное уравнение имеет три решения при тех
значениях параметра р, при которых
горизонтальная прямая имеет три точки
пересечения с параболами. Таким образом,
уравнение (3) имеет три решения в следующих
случаях:
1) прямая проходит через вершину одной параболы
и пересекает другую в двух точках. Это возможно,
когда т.е.
при
уравнение имеет три решения;
2) прямая проходит через точку пересечения
парабол. Найдём абсциссу точки пересечения
парабол, для этого решим уравнение
Если то
т.е. при
прямая
пересекает параболы в трех точках, значит,
исходное уравнение имеет три корня.
Ответ:
Задача 4. При каких значениях параметра а
существует единственная пара (х; у),
удовлетворяющая уравнению
(4)
Решение: Уравнение – квадратное
относительно х.
(5)
1. Контрольным значением параметра является
число , при
котором уравнение (5) примет вид отсюда
. Видно, что в этом случае
решениями уравнения будут все пары , т.е. при
исходное уравнение имеет
бесконечное множество решений.
2. Пусть .
Дискриминант уравнения (5)
Если т.е.
, то
, исходное
уравнение имеет решение только тогда, когда , а
— единственное решение.
Если же ,
исходное уравнение относительно х имеет
решение при любом у.
Ответ: .
Задача 5. Решите уравнение
(6)
относительно х
Решение. Уравнение является квадратным
относительно р. Перепишем уравнение (6) в виде
(7)
Дискриминант квадратного уравнения (7)
Решая (7), получим
Здесь возможны случаи.
1. Уравнение (6) имеет четыре корня, если
Решая систему, получаем . Таким образом, при
уравнение (6) имеет четыре
корня ,
2. Уравнение (6) имеет три корня, если
Решая систему, получим Значит, при
уравнение (6) имеет три корня
3. Уравнение (6) имеет два корня, если
Решая систему, получим , значит, при этих значениях
параметра р уравнение (6) имеет два корня
4. Уравнение (6) имеет один корень, если
Решая систему, получим . Следовательно, при
решением уравнения (6)
будет .
5. Уравнение (5) не имеет корней, если
Ответ: если — корней нет;
если
если ;
если
если
Этот метод не является универсальным, но во
многих случаях является весьма результативным и
позволяет решать уравнения повышенной
сложности. Иногда трудно предвидеть будет ли
применение этого метода результативным, но такие
уравнения существуют и поэтому его надо знать.
Например, с помощью этого метода можно решить
следующие уравнения:
из
сборника для подготовки к ЕГЭ.
из
сборника Сканави
и другие.
Решение уравнений с параметрами
Зверяка Светлана Усманбаевна, преподаватель математики ОП «Луганский профессиональный торгово-кулинарный колледж ЛНУ имени Тараса Шевченко», специалист І категории
Коробова Елена, обучающаяся 68 группы ОП «ЛПТКК ЛНУ им. Тараса Шевченко»
«Метод решения хорош,
если с самого начала мы можем предвидеть –
и далее подтвердить это, — что,
следуя этому методу, мы достигнем цели.»
Г. Лейбниц
В повседневной жизни мы очень часто сталкиваемся с понятием параметра: параметр загрузки в Windows 10, параметры бытовых приборов, параметры автомобиля. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др… Исследование многих жизненных процессов осуществляется с помощью параметров. Например, состояние больного определяется с помощью параметров температуры, давления. Для оценки состояния спортсмена в качестве параметра используется частота сердечных сокращений. Положение движущегося тела в пространстве определяется параметром времени. В изолированном сосуде данного объема давление газа характеризуется параметром температуры.
Толковый словарь определяет параметр как величину, характеризующую какое-нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999). Рассмотрение параметров — это всегда выбор. Перед выбором мы стоим и в различных жизненных ситуациях.
Вспомним сказку. В чистом поле стоит столб, а настолбу написаны слова: «Кто поедет от столба сего прямо, тот будет голоден и холоден; кто поедет в правую сторону, тот будет здрав и жив, а конь его будет мертв; а кто поедет в левую сторону, тот сам будет убит, а конь его жив и здрав останется!» Иван-царевич прочел эту надпись и поехал в правую сторону, держа на уме: хоть конь его и убит будет, зато сам жив останется и со временем сможет достать себе другого коня. (“Иван-царевич и серый волк” Русская народная сказка).
Но это в сказке, а что же собой представляет параметр в математике? Какую роль он играет при решении уравнений? Какими методами решаются уравнения с параметрами?
Актуальность данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдаче государственной итоговой аттестации и на вступительных экзаменах в высшие учебные заведения.
Цель данной работы систематизировать уравнения, содержащие параметр, и составить алгоритм их решения с учетом свойств различных функций.
Для достижения поставленной цели необходимо решить следующие задачи:
1) дать определения понятиям «уравнение с параметрами»;
2) показать принцип решения данных уравнений на общих случаях;
3) показать решение уравнений с параметрами, связанных со свойствами линейной, квадратичной, рациональной и иррациональной функциями, используя различные методы.
4) составить алгоритм решения уравнений с параметрами, с учетом свойств различных функций.
Для выполнения поставленной цели были использованы следующие методы: изучение и анализ литературы разного типа, работа в группах на уроках алгебры и факультативных занятиях по математике, апробация полученных результатов на уроках математики.
Объектом исследовательской работы было решение уравнений с параметрами, связанных со свойствами выше представленных функций.
Мы выбрали эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, была ставлена цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Данная работа поможет понять другим ученикам, как решаются уравнения с параметрами, применяя аналитический и графического методы, узнать о происхождении таких уравнений. В работе приводятся теоретические основы решения уравнений, содержащих параметр. Рассмотривается аналитический и графический способы решения основных видов уравнений, содержащих параметр.
В работе рассмотрены часто встречающиеся типы уравнений, и, надеемся, что знания, полученные нами в процессе работы, помогут при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на ГИА. В первой части изложен наиболее стандартный, аналитический способ решения уравнений, а во второй – графический.
Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ,
СОДЕРЖАЩИХ ПАРАМЕТР
Основной принцип решения параметрических уравнений можно сформулировать так: необходимо разбить область изменения параметра на участки, такие, что при изменении параметра в каждом из них получающиеся уравнения можно решить одним и тем же методом. Отдельно для каждого участка находятся корни уравнения, выраженные через значения параметра, используемые для этого приемы в точности таковы, как и при решении уравнений с постоянными коэффициентами. Поскольку каждый из методов представляет собой последовательность определенных действий, которые могут выполняться по-разному в зависимости от значений параметра, то выбранные первоначально участки его изменения в процессе решения могут дробиться с тем, чтобы на каждом из них рассуждения проводились единообразно. Ответ задачи состоит из списка участков изменения параметра с указанием для каждого участка всех корней уравнения.
Для разбиения множества значений параметра на участки удобно воспользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра будем называть контрольными.
Основное, что нужно усвоить при решении таких уравнений. Параметр – это буква, которая «никому ничем не обязана» и может принимать любые допустимые значения. Поэтому с ней нужно необходимость осторожно, даже деликатно, помня, что это фиксированное, но неизвестным числом.
2.1. История возникновения уравнений с параметром
Задачи на уравнения с параметром встречались уже в астрономическом трактате «Ариабхаттиам», составленном в 499г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
В уравнении коэффициенты, кроме параметра a, могут быть и отрицательными.
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений с параметром а. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е.
2) «Квадраты равны числу», т. е.
3) «Корни равны числу», т. е
4) «Квадраты и числа равны корням», т. е.
5) «Квадраты и корни равны числу», т. е.
6) «Корни и числа равны квадратам», т. е.
Формулы решения квадратных уравнений по Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи.
Вывод формулы решения квадратного уравнения с параметром в общем виде имеется у Виета, однако Виета признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принял современный вид.
История возникновения графического метода далеко уходит в древние века. Исследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. При таком характере не оставалось места изучению количественных зависимостей, речь шла лишь о качествах предметов и их связях друг с другом.
Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им «линией интенсивностей» или «линией верхнего края» (график соответствующей функциональной зависимости). Оресм изучал даже «плоскостные» и «телесные» качества, т.е. функции, зависящие от двух или трех переменных.
Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: Равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств.
Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.
Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций — неотъемлемая часть истории современной алгебры и геометрии.
Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический.
2.2. Теорема Виета
Теорема, выражающая связь между параметрами, коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. Следующим образом: «Если b + d, умноженное на α минус α2, равно bc, то α равно b и равно d».
Чтобы понять Виета, следует вспомнить, что α, как и всякая гласная буква, означала у него неизвестное (наше х), гласные же b, d – коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает:
Если имеет место
(α + b)x – x2 = αb,
Т. е. x2 — (α –b)x + αb =0,
то x1 = α, x2 = b.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виета установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
2.3. Аналитический метод решения задач с параметрами.
2.3.1. Линейные уравнения с параметрами
Уравнение вида , где – некоторые постоянные, называется линейным уравнением.
Если , то линейное уравнение имеет единственный корень: .
Если , переписав исходное уравнение в виде , легко видеть, что любое х является решением линейного уравнения.
Если а, то линейное уравнение не имеет корней.
Класс линейных уравнений с параметром выделяется с помощью двух характеристик:
1. В уравнении переменная х находится в первой степени;
2. При помощи равносильных преобразований на области допустимых значений параметра уравнение приводится к стандартному виду
Основываясь на основные свойства линейной функции, можно составить алгоритм решения. В зависимости от вида уравнения некоторые пункты его могут быть опущены (Приложение 1).
Пример 1.
Решить уравнение: , если а– параметр.
1. Область допустимых значений параметра – вся числовая прямая.
2. Приведем уравнение к виду.
3. Контрольными являются те значения параметра, при которых коэффициент при х обращается в нуль. Такими значениями будут.
4. Если , то уравнение примет вид . Это уравнение не имеет корней.
Если , то уравнение примет вид . Корнем этого уравнения является любое действительное число.
5. Если , то , .
Ответ: если , то корней нет;
если , то ;
если , то .
Пример 2.
Решить уравнение: , если а– параметр.
1. Область допустимых значений параметра – вся числовая прямая.
2. Приведем уравнение к виду .
3. Контрольные значения параметра: .
4. Если , то уравнение примет вид . Это уравнение не имеет корней.
Если , то уравнение примет вид. Корнем этого уравнения является любое действительное число.
5. Если , то .
Ответ: если , то корней нет;
если , то ;
если , то .
Пример 3.
Решить уравнение:
-
Область допустимых значений параметра – вся числовая прямая.
-
Приведем уравнение к виду
-
Контрольные значения параметра: .
-
если , то уравнение принимает вид , x
-
если , то уравнение имеет один корень
,
Ответ: если , то
если , то
2.3.2. Квадратные уравнения, содержащие параметр
Класс уравнений второй степени с параметрами определяется с помощью двух характеристик:
1. Переменная х в уравнении находится в первой и второй степенях;
2. При помощи равносильных преобразований на области допустимых значений параметра уравнение приводится к стандартному виду
.
Контрольные значения параметра определяются дискриминантом D. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из типов:
-
Если , то уравнение имеет два корня:
-
Если , то уравнение имеет один корень кратности два или два равных корня
-
Если , то уравнение не имеет действительных корней.
Тогда решением всякого уравнения с параметром не выше второй степени осуществляется по следующим этапам:
-
На числовой прямой отмечаются все контрольные значения параметра, для которых соответствующие частные уравнения не определены.
-
На области допустимых значений параметра исходного уравнения при помощи равносильных преобразований приводится к виду .
-
Выделяют множество контрольных значений параметра, для которых .
Если уравнение имеет конечное множество решений, то для каждого найденного контрольного значения параметра соответствующее частное уравнение решается отдельно. Проводится классификация частных уравнений по первым трем типам.
На бесконечном множестве решений уравнения проводится решение уравнения , выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых и , соответствует третий тип не особых частных уравнений.
-
Выделяются контрольные значения параметра, для которых дискриминант обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный корень .
-
Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков определяется знак дискриминанта.
Множеству значений параметра, для которых и, соответствует тип не особых частных уравнений, не имеющих решений, для значений параметра из множества, где и , частные уравнения имеют два различных действительных корня [Горнштейн, П.И. Задачи с параметрами: учеб.пособие/ П.И. Горнштейн, В.Б. Полонский, М.С. Якир – Киев, 1992.],[5],[19].
Из этого следует алгоритм решения квадратных уравнений с параметрами. В зависимости от вида уравнения некоторые пункты его могут быть опущены (Приложение 2)
Пример4.
Решить уравнение: .
-
Область допустимых значений параметра – вся числовая прямая.
-
Контрольным значением параметра является .
при уравнение будет линейное
при уравнение будет квадратным
-
Если , то уравнение примет вид . Отсюда .
-
При уравнение является квадратным. Найдем дискриминант уравнения:
.
-
Контрольное значение параметра
-
Если .
-
Оценим знак дискриминанта
+ +
— 0,8 1
-
Если и действительных корней нет.
Если .
Ответ:
, то корней нет;
;
.
Пример 5.
Решить уравнение
-
Область допустимых значений параметра – вся числовая прямая.
-
Контрольное значение параметра .
-
Если , то уравнение будет линейным и примет вид
-
Если , то уравнение будет квадратным с дискриминантом
-
Контрольное значение параметра .
-
Если
-
Оценим знак дискриминанта
+ + +
0 1
-
Если
Ответ: если ;
если ;
если.
Пример 6.
Решить уравнение:
-
Область допустимых значений параметра – вся числовая прямая.
-
Контрольное значение параметра.
-
Если , то уравнение будет линейным и примет вид
-
Если , то получим квадратное уравнение с дискриминантом
-
Контрольные значения параметра
-
Если получаем ,
если
-
Оценим знак дискриминанта
– + + –
1 2 6
-
Если 1< а < 2 и 2< а < 6 , то дискриминант положителен и уравнение имеет два корня
-
Если уравнение корней не имеет.
Ответ: если , то корней нет;
если
если
если ;
если
если ;
если, то корней нет.
Пример 7.
Сколько корней может иметь при различных значениях параметра b уравнение ?
-
Область допустимых значений параметра – вся числовая прямая.
-
Приведем уравнение к виду .
-
Контрольное значение параметра: .
-
Если и уравнение имеет один корень.
-
Оценим знак дискриминанта
+ –
0,25
-
Если и уравнение не имеет корней.
Если и уравнение имеет два различных корня.
Ответ: уравнение имеет два различных корня, при — один корень, при уравнение не имеет корней.
Обобщив простейшие случаи соотношения между двумя корнями квадратного уравнения, образуем математические модели (Приложение 3).
2.3.3. Рациональные уравнения, содержащие параметр,
сводящиеся к линейным
Процесс решения рациональных уравнений протекает по обычной схеме. Данное уравнение заменяется целым, путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решают известным способом целое уравнение, исключая посторонние корни, то есть числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы посторонние корни исключить, требуется находить значение параметра, обращающее общий знаменатель в нуль, то есть решать соответствующие уравнения относительно параметра [Горнштейн, П.И. Задачи с параметрами: учеб.пособие/ П.И. Горнштейн, В.Б. Полонский, М.С. Якир – Киев, 1992.].
Пример 8.
Решить уравнение: .
-
Область допустимых значений:
-
Контрольное значение параметра
-
При , уравнение не имеет корней.
-
Если,то:.
-
Найдем дискриминант уравнения.
-
Находим корни уравнения:.
-
При приведении к общему знаменателю, расширилась область определения уравнения, что могло привести к появлению посторонних корней. Поэтому необходима проверка.
Проверка. Исключим из найденных значений хтакие, при которых
.
Если
Таким образом, при посторонний корень уравнения.
Если
Таким образом, при —посторонний корень уравнения.
Если .
Таким образом, при посторонний корень уравнения.
Если .
Таким образом, при —посторонний корень уравнения.
При получаем;
При
.
Ответ:
2.3.4. Иррациональные уравнения, содержащие параметр
Главными особенностями при решении уравнений такого типа являются:
-
ограничение области определения неизвестной х, так как она меняется в зависимости от значения параметра.
-
в решении уравнений вида при возведении в квадрат необходимо учитывать знак и проводить проверку корней.
При рассмотрении всех особых случаев и возведении обеих частей иррационального уравнения в квадрат мы переходим к решению квадратного уравнения с параметром.
Рассмотрим несколько примеров и попробуем заметить эти особенности при решении [Горнштейн, П.И. Задачи с параметрами: учеб.пособие/ П.И. Горнштейн, В.Б. Полонский, М.С. Якир – Киев, 1992.].
Пример 9.
Решить уравнение:.
-
Перепишем исходное уравнение в виде:
-
Возведем в квадрат обе части иррационального уравнения с последующей проверкой полученных решений.
3.Контрольное значение параметра Особое значение: а = 0,5.
Отсюда:
-
при
-
при ;
-
при уравнение не имеет решений.
Проверка:
-
при подстановке в уравнение, равносильное исходному, получим неверное равенство. Значит, не является решением уравнения.
-
при подстановке в получим:
Так как левая часть равенства отрицательна, то х2 не удовлетворяет исходному уравнению.
-
Подставим в уравнение:
Проведя равносильные преобразования, получим:
Если , то можно возвести полученное равенство в квадрат:
.
Имеем истинное равенство при условии, что .
Это условие выполняется, если . Так как равенство истинно при может быть корнем уравнения при а > 0,5, следовательно, х1– корень уравнения при а≥1.
Ответ.
-
при а ≥ 1 х = 0,5∙(1 + );
-
приа<1 уравнение не имеет решений.
2.4. Графически метод решения задач с параметрами.
График функции — понятие, которое даёт представление о геометрическом образе функции, т. е. это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:точка (x,y) располагается (или находится) на графике функции f тогда и только тогда, когда y=f(x).
Таким образом, функция может быть адекватно описана своим графиком.
Графический метод решение уравнений с параметром на первый взгляд очень прост. Необходимо построить график данной функции, рассечь его прямыми найти точки пересечения и выписать ответ. Однако, он имеет ряд особенностей, основанных на нахождении всех точек данной плоскости, координаты которых удовлетворяют заданному в условии соотношению. При этом используются различные системы координат: (хОу), (хОа), (аОх). Их выбор обусловлен особенностями уравнения и простотой построения графиков.
При графическом решении уравнения с параметром необходимо:
-
Найти область определения уравнения, т.е. область допустимых значений неизвестного и параметра, при которых уравнение может иметь решения.
-
Выразить параметр как функцию от x:
-
В системе координат (хОу) построить графики функций и для тех значений х, которые входят в область определения уравнения.
-
Определить точки пересечения прямой с графиком функции .
Возможны ситуации:
-
Прямая не пересекает график . Следовательно, при данном значении а исходное уравнение решений не имеет.
-
Прямая пересекает график в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.
Пример 10.
Решить уравнение:
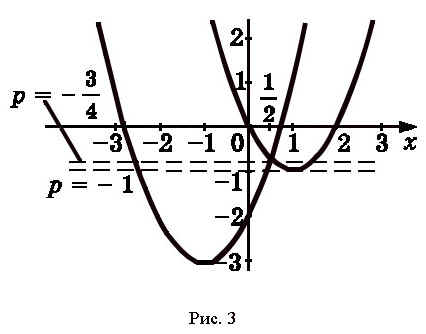
Решением данного уравнения будут точки пересечения графиков (Парабола у = х2, смещенная вверх на одну единицу) и (Прямая, параллельная оси Ох)
В зависимости от параметра а, уравнение имеет несколько решений:
если а < 0, прямая у = а не пересекает график у = х2 + 1;
если0 ≤ а < 1 прямая у = а не пересекает параболу;
если а = 1 парабола и прямая имеют единственную точку пересечения;
при а > 1 таких точек пересечения две.
Ответ: а < 1 – корней нет,
а = 1 – единственный корень,
а > 1 – два корня.
Пример 11.
Найти все значения а, при каждом из которых уравнение имеет восемь различных решений.
Решение: 1 способ. ,
Построим графики функций при и .
Графиком первой функции является семейство парабол с вершинами, расположенных на оси Оу: у=0, и т.д. (в зависимости от k=0,1,2,3,4,…).
Графиком второй функции является прямая, параллельная осиОх.
По графику определяем, что восемь решений (точек пересечения) возможно в том случае, если прямая расположена выше прямойно ниже прямой . Следовательно, , .
При ,
при .
Ответ: ,
Решение: 2 способ. , Заметим, что параметр а может принимать как положительные, так и отрицательные значения, но не равен нулю.
Построим график функции при у>0 , т.е. или (полуокружность с центром в начале координат) . Графиком второй функции при является семейство прямых, параллельных осиОх, проходящих через точки с ординатами у=0, , , , и т.д.
Рассмотрим полуокружность радиуса r=a. Если радиус , то полуокружность пересекает серию прямых в восьми точках. Аналогично рассуждаем для случаяа<0.
Ответ: ,
Пример 12.
Найти число решений уравнения .
Решение: Заметим, что х не равно нулю. Умножим обе части уравнения на. Получим
Построим график функции .
Графиком функции является прямая, параллельная осиОх.
Анализируя графическую иллюстрацию, понятно, что при а=0 одно решение, т.к. одна точка пересечения (не забываем, что х не равен нулю). При а=1 две точки пересечения графика функции и прямой, а значит и два решения. При а<0 получается одна точка пересечения, как и при а>1. Если же , то график функции и прямая имеют три точки пересечения.
Ответ: при, одно решение,
при два решения, при три решения.
Таким образом, графический метод обладает целым рядом преимуществ перед аналитическим: он более нагляден и понятен в случаях, когда необходимо ответить на качественный вопрос или провести анализ множества решений. Однако следует помнить, что универсальных методов и приёмов, пригодных для любой математической задачи, не существует. Поэтому, приступая к анализу того или иного уравнения, необходимо выбрать наиболее эффективный из возможных способов его решения.
ВЫВОДЫ
Изучив данную тему, можем сделать вывод. Параметр – это буква, которая «никому ничем не обязана» и может принимать любые допустимые значения. Структура решений уравнения зависит от значений параметра; те или иные аспекты этой зависимости и предстоит выяснять в каждой конкретной задаче. Для этого нужно использовать различные формы и методы решения, с учетом свойств каждой конкретной функции.
Как известно, очень узкий класс уравнений решаются по формулам. Это линейные, квадратные, кубические уравнения. Для решения других уравнений используется метод замены переменной или метод разложения на множители. Данные методы позволяют рационально решать сложные уравнения, а порой являются и единственными способами. Для того, чтобы овладеть этими методами, необходимо иметь прочные навыки по стандартным методам, преобразованиям, знать много теоретического материала и дополнительно решать.
Исследовав данную тему, мы пришли к выводу, что нет определённой структуры при решении уравнений с параметрами. Формы и методы решения определяются для каждого задания индивидуально, анализируя конкретную функцию и ее свойства. Поэтому ход решения определяется видом функции, линейной или квадратичной. Рациональные и иррациональные уравнения, путем математических преобразований, сводятся к решению линейных или квадратных. Только в иррациональных не следует забывать о посторонних корнях, обязательно делается проверка.
Графический метод очень удобен, когда выведение параметра, приводит определенной функцию, т.е. явно выражена a=const.
Выведенные алгоритмы решения уравнений были опробованы на уроках математики и факультативных занятиях. Их применение существенно сократило время, затраченное на решения.
Используя алгоритмы решения, представленный в данной работе, на уроках математики и при самостоятельной подготовке к сдаче государственную итоговую аттестацию и ГИА, учащиеся смогут быстро находить рациональные решения уравнений с параметрами.
Работа над данной темой была интересной и познавательной. Изучив методы решения уравнений с параметрами, мы обогатили свой опыт:
• новыми научными понятиями;
• узнали методы, которые выходят за рамки школьной программы;
• углубили и расширили свои знания.
Работа над проектом позволила приобрести опыт выполнения научной работы.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
Горнштейн, П.И. Задачи с параметрами: учеб.пособие/ П.И. Горнштейн, В.Б. Полонский, М.С. Якир – Киев, 1992.
-
Дорофеев, Г.В. Квадратный трехчлен в задачах. – Львов: Квантор, 1991.
-
Здоровенко, М.Ю. Учимся решать задачи с параметрами: рациональные уравнения и неравенства./ М.Ю. Здоровенко, В.М. Караулов – Киров, 1999.
-
Ястребинецкий Г.А. Задачи с параметрами: Книга для учителя. – М.: Просвещение, 1986.
-
Горбачев, В.И. Общие методы решения уравнений и неравенств с параметрами не выше второй степени / В.И. Горбачев// Математика в школе – 2000. — №2. – С. 61-68.
-
Джиоев, Н.Д. Нахождение графическим способом числа решений уравнений с параметром / Н.Д. Джиоев // Математика в школе – 1996. — №2. – С. 54-57.
-
Евсеева, А.И. Уравнения с параметрами / А.И. Евсеева // Математика в школе – 2003. — №7. – С. 10-17.
-
Епифанова, Т.Н. Графические методы решения задач с параметрами / Т.Н. Епифанова// Математика в школе – 2003. — №7. – С. 17-20.
-
Кожухов, С.К. Об одном классе параметрических задач / С.К. Кожухов // Математика в школе – 1996. — №3. – С. 45-49.
-
Кожухов, С.К. Различные способы решения задач с параметром / С.К. Кожухов // Математика в школе – 1998. — №6. – С. 9-12.
-
Кормихин, А.А. Об уравнениях с параметром / А.А. Кормихин // Математика в школе – 1994. — №1. – С. 33-35.
-
Кочерова, К.С. Об уравнениях с параметром и модулем (графический способ решения) / К.С. Кочерова// Математика в школе – 1995. — №2. – С. 2-4.
-
Мещерякова, Г.П. Задачи с параметрами, сводящиеся к квадратным уравнениям / Г.П. Мещерякова // Математика в школе – 2001. — №5. – С. 60-62.
-
Мещерякова, Г.П. Функционально-графический метод решения задач с параметром / Г.П. Мещерякова // Математика в школе – 1999. — №6. – С. 69-71.
-
Постникова, С.Я. Уравнения с параметрами на факультативных занятиях / С.Я. Постникова// Математика в школе – 2002. -№ 8. – С. 45-46.
-
Потапов, М.К., Шевкин А.В. О решении уравнений вида / М.К. Потапов// Математика в школе – 2003. -№8. – С. 12-14.
-
Ратников. Н.П. От уравнения с параметром – к графику, задающему параметр / Н.П. Ратников // Математика в школе – 1990. — №3. – С. 80.
-
Теоретические основы решения уравнений с параметрами/[Электронный ресурс]. – Режим доступа: http://parametry.narod.ru/uravneniya.html
-
Заслонкина Л. С. Задачи с параметрами // Библиотека к журналу математика в школах Украины – Х.: Основа, 2012.
-
Уравнения и неравенства с параметрами: количество решений/[Электронный ресурс]. – Режим доступа:http://abkov.ru/ege/2011-mys/C5-2011-Kornv.pdf
ПРИЛОЖЕНИЯ
Приложение 1
Алгоритм решения линейных уравнений с параметрами:
1. Найти область допустимых значений параметра.
2. Привести уравнение к стандартному виду.
3. Найти контрольные значения параметра.
4. Решить частные уравнения для контрольных значений параметра .
5. Для остальных значений параметра найти общие решения по формуле
6. Записать ответ.
В зависимости от вида уравнения некоторые пункты алгоритма могут быть опущены.
Приложение 2
Алгоритм решения квадратных уравнений с параметрами:
-
Найти область допустимых значений параметра.
-
Привести уравнение к стандартному виду.
-
Найти контрольные значения параметра из уравнения .
-
На множестве без найденных контрольных значений параметра составить квадратное уравнение и найти его дискриминантD.
-
Найти контрольные значения параметра из уравнения D = 0.
-
Решить частные уравнения для контрольных значений параметра.
-
На выделенных промежутках значений параметра оценить знак D.
-
Решить частные уравнения, не имеющие решений и имеющие два различных действительных корня.
-
Записать ответ.