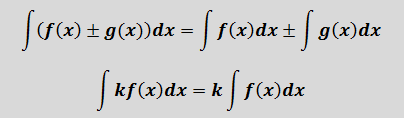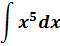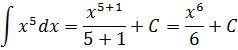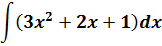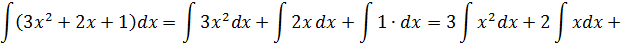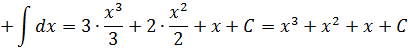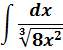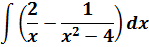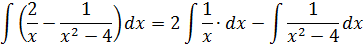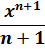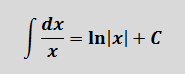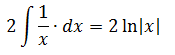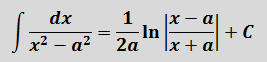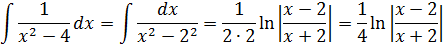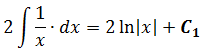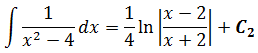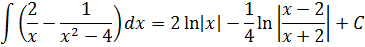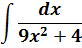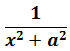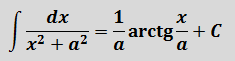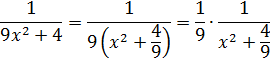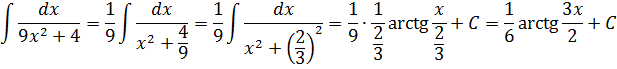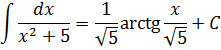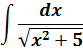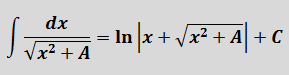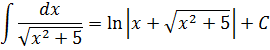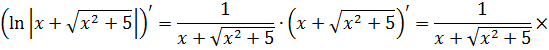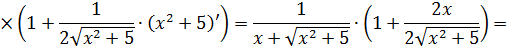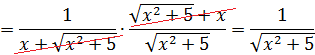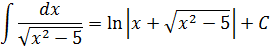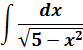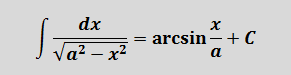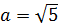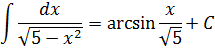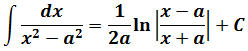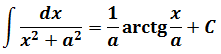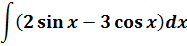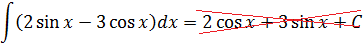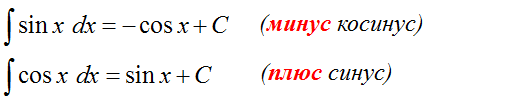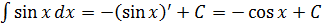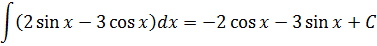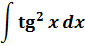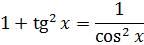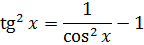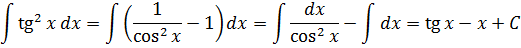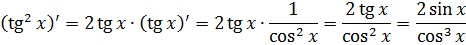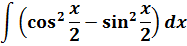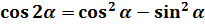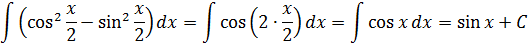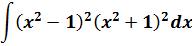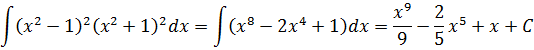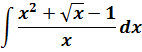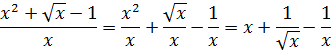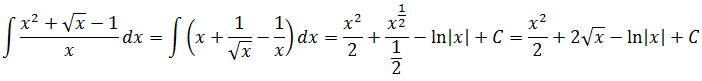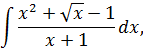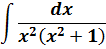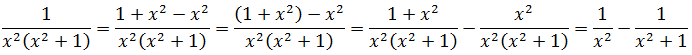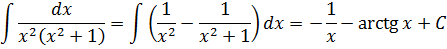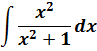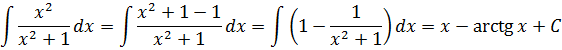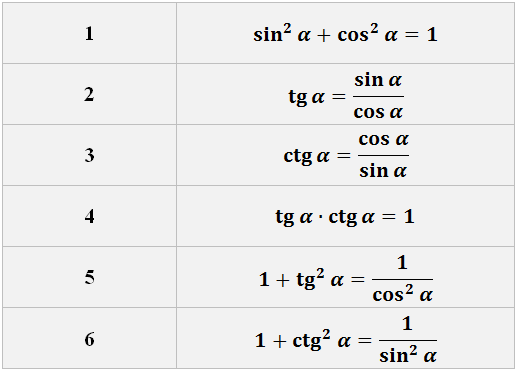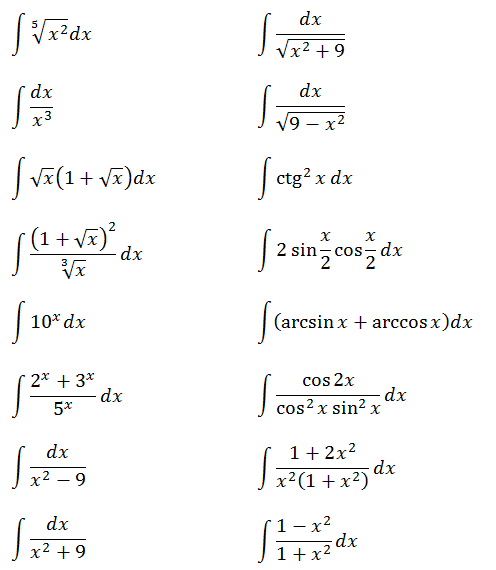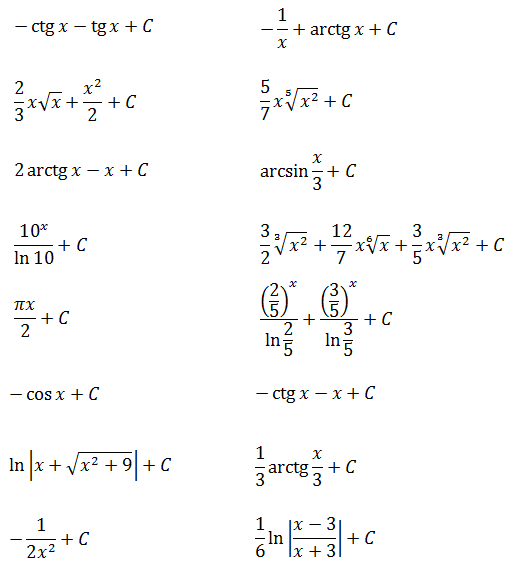Содержание
- Обратное свойство
- Неопределенный интеграл
- Другие значения постоянной интеграции
- Как рассчитывается постоянная интегрирования?
- Примеры
- Пример 1
- Пример 2
- Пример 3
- Предлагаемые упражнения
- Упражнение 1
- Упражнение 2.
- Упражнение 3.
- Упражнение 4.
- Ссылки
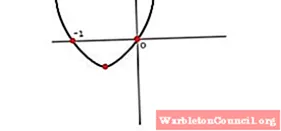
В постоянная интеграции Это дополнительная ценность для вычисления первообразных или интегралов, она служит для представления решений, составляющих примитив функции. Он выражает внутреннюю неоднозначность, когда любая функция имеет бесконечное количество примитивов.
Например, если мы возьмем функцию: f (x) = 2x + 1 и получим ее первообразную:
∫ (2x + 1) dx = х2 + х + C ; куда C это постоянная интеграции и графически представляет вертикальный переход между бесконечными возможностями примитива. Правильно сказать, что (x2 + x) есть а примитивов f (x).
Таким же образом вы можете определить (x2 + х + C ) как примитив f (x).
Обратное свойство
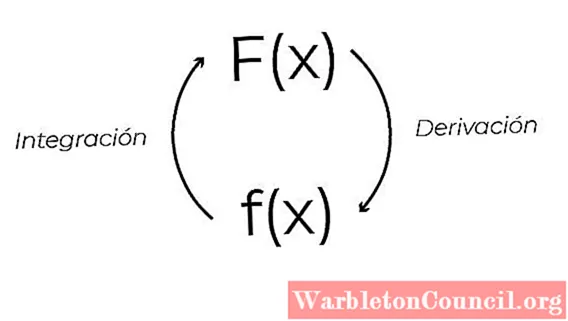
Можно отметить, что при выводе выражения (x2 + x), мы получаем функцию f (x) = 2x + 1. Это связано с обратным свойством, существующим между выводом и интегрированием функций. Это свойство позволяет получать формулы интегрирования, начиная с дифференцирования. Это позволяет проверять интегралы через те же производные.
Однако (x2 + x) — не единственная функция, производная которой равна (2x + 1).
- d (Икс2 + х) / dx = 2x + 1
- d (Икс2 + х + 1) / dx = 2x + 1
- d (Икс2 + х + 2) / dx = 2x + 1
- d (Икс2 + х + 3) / dx = 2x + 1
- d (Икс2 + х + C) / dx = 2x + 1
Где 1, 2, 3 и 4 представляют конкретные примитивы f (x) = 2x + 1. В то время как 5 представляет неопределенный или примитивный интеграл f (x) = 2x + 1.
Примитивы функции получаются посредством первичного или интегрального процесса. Где F будет примитивом f, если верно следующее
- у = ∫ f (x) dx= F (х) + С; C = постоянная интеграции
- F ’(x) = f (x)
Можно видеть, что функция имеет единственную производную, в отличие от ее бесконечных примитивов, полученных в результате интегрирования.
Неопределенный интеграл
∫ f (x) dx = F (x) + C
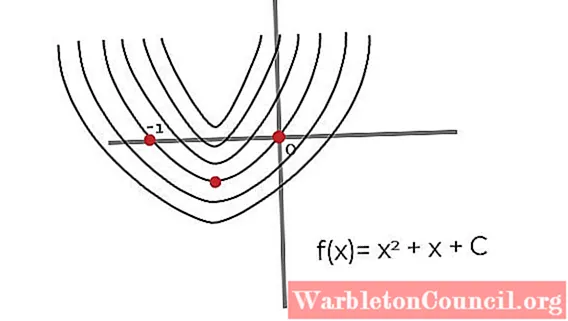
Он соответствует семейству кривых с одинаковым рисунком, которые испытывают несоответствие в значениях изображений каждой точки (x, y). Каждая функция, отвечающая этому шаблону, будет отдельным примитивом, а набор всех функций известен как неопределенный интеграл.
Ценность постоянная интеграции именно он отличает каждую функцию на практике.
В постоянная интеграции предлагает вертикальный сдвиг на всех графиках, которые представляют примитивы функции. Где наблюдается параллелизм между ними, и то, что C это значение смещения.
Согласно общепринятой практике постоянная интеграции он обозначается буквой «C» после добавления, хотя на практике не имеет значения, добавляется или вычитается константа. Его реальную ценность можно найти разными способами в зависимости от первоначальные условия.
Другие значения постоянной интеграции
Уже говорилось о том, как постоянная интеграции применяется в отрасли интегральное исчисление; Представление семейства кривых, определяющих неопределенный интеграл. Но многие другие науки и отрасли приписывают очень интересные и практические ценности постоянная интегрирования, которые способствовали развитию множества исследований.
в физический константа интегрирования может принимать несколько значений в зависимости от характера данных. Очень распространенный пример — знание функции V (т) который представляет собой скорость частицы в зависимости от времени t. Известно, что при вычислении примитива V (t) функция получается R (t) который представляет собой позиция частицы против времени.
В постоянная интеграции он будет представлять значение начальной позиции, то есть в момент t = 0.
Аналогично, если функция известна В) который представляет собой ускорение частицы против времени. Примитив A (t) приведет к функции V (t), где постоянная интеграции будет значением начальной скорости V0.
в экономия, получая посредством интегрирования примитив функции стоимости. В постоянная интеграции будут представлять собой постоянные затраты. И так много других приложений, заслуживающих дифференциального и интегрального исчисления.
Как рассчитывается постоянная интегрирования?
Для расчета постоянная интегрирования, всегда будет необходимо знать первоначальные условия. Которые отвечают за определение того, какой из возможных примитивов является соответствующим.
Во многих приложениях он рассматривается как независимая переменная в момент времени (t), где постоянная C принимает значения, которые определяют первоначальные условия конкретного случая.
Если взять исходный пример: ∫ (2x + 1) dx = x2 + х + C
Допустимое начальное условие может заключаться в том, что график проходит через определенную координату. Например, известно, что примитив (x2 + х + C) проходит через точку (1, 2)
F (х) = х2 + х + C; это общее решение
F (1) = 2
Подставим в это равенство общее решение
F (1) = (1)2 + (1) + С = 2
Отсюда легко следует, что C = 0
Таким образом, соответствующий примитив для этого случая есть F (х) = х2 + х
Есть несколько типов числовых упражнений, которые работают с константы интегрирования. Фактически, дифференциальное и интегральное исчисление не перестают применяться в современных исследованиях. Их можно найти на разных академических уровнях; от первоначального расчета, через физику, химию, биологию, экономику и другие.
Это также видно при изучении дифференциальные уравнения, где постоянная интеграции Он может принимать разные значения и решения, это связано с многочисленными производными и интеграциями, которые выполняются в этом вопросе.
Примеры
Пример 1
- Пушка высотой 30 метров стреляет вертикально вверх. Известно, что начальная скорость снаряда составляет 25 м / с. Принимать решение:
- Функция, определяющая положение снаряда по времени.
- Время полета или момент, когда частица падает на землю.
Известно, что при прямолинейном движении, равномерно изменяющемся, ускорение является постоянной величиной. Это случай запуска снаряда, где ускорение будет равным гравитации.
g = — 10 м / с2
Также известно, что ускорение — это вторая производная от положения, что указывает на двойное интегрирование в разрешении упражнения, таким образом, получая два константы интегрирования.
А (т) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
Начальные условия упражнения указывают на то, что начальная скорость равна V0 = 25 м / с. Это скорость в момент времени t = 0. Таким образом выполняется следующее:
V (0) = 25 = -10 (0) + C1 Y C1= 25
С определенной функцией скорости
V (t) = -10t + 25; Сходство с формулой MRUV (VF = V0 + а х т)
Аналогичным образом мы продолжаем интегрировать функцию скорости, чтобы получить выражение, определяющее положение:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5t2 + 25т + C2
R (t) = -5t2 + 25т + C2 (примитив позиции)
Начальное положение R (0) = 30 м известно. Затем вычисляется конкретный примитив снаряда.
R (0) = 30 м = -5 (0)2 + 25(0) + C2 . куда C2 = 30
Первый раздел разрешен, так как R (t) = -5t2 + 25т + 30 ; Это выражение гомологично формуле смещения в MRUV R (t) = R0 + V0т — гт2/2
Для второго раздела необходимо решить квадратное уравнение: -5t2 + 25т + 30 = 0
Поскольку это заставляет частицу достигнуть земли (позиция = 0)
Фактически, уравнение 2-й степени дает нам 2 решения T: {6, -1}. Значение t = -1 игнорируется, потому что это единицы времени, домен которых не включает отрицательные числа.
Таким образом решается второй участок, где время полета равно 6 секундам.
Пример 2
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (x) = 4; f ‘(2) = 2; f (0) = 7
Когда информация о второй производной f ’’ (x) = 4, начинается процесс антидеривации.
f ’(x) = ∫f’ ’(x) dx
∫4 dx = 4x + C1
Затем, зная условие f ‘(2) = 2, переходим:
4 (2) + С1 = 2
C1 = -6 и f ’(x) = 4x — 8
Проделайте то же самое для второго постоянная интеграции
f (x) = ∫f ’(x) dx
∫ (4x — 
Начальное условие f (0) = 7 известно и приступаем:
2(0)2 — 8 (0) + С2 = 7
C2 = 7 и f (x) = 2x2 — 8x + 7
- f ’’ (x) = x2 ; f ‘(0) = 6; f (0) = 3
Аналогично предыдущей задаче мы определяем первые производные и исходную функцию из начальных условий.
f ’(x) = ∫f’ ’(x) dx
∫ (х2) dx = (x3/ 3) + С1
При условии f ‘(0) = 6 переходим:
( 03/ 3) + С1 = 6; куда1 = 6 и f ’(x) = (x3/3 ) + 6
Затем второй постоянная интеграции
f (x) = ∫f ’(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + С2
Начальное условие f (0) = 3 известно и приступаем:
[(0)4/ 12] + 6 (0) + C2 = 3; куда2 = 3
Таким образом, мы получаем примитивное частное
f (x) = (Икс4/ 12) + 6x + 3
Пример 3
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = 2x — 2, который проходит через точку (3, 2)
Важно помнить, что производные относятся к наклону линии, касательной к кривой в данной точке. Где некорректно предполагать, что график производной касается указанной точки, поскольку она принадлежит графику примитивной функции.
Таким образом, мы выражаем дифференциальное уравнение следующим образом:
dy = (2х — 2) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (2x — 2) dx
у = х2 — 2x + C
Применение начального условия:
2 = (3)2 — 2 (3) + С
С = -1
Получается: f (х) = х2 — 2х — 1
- dy / dx = 3x2 — 1, который проходит через точку (0, 2)
Выразим дифференциальное уравнение следующим образом:
dy = (3x2 — 1) дх ; тогда при применении критериев предотвращения вывода мы имеем:
∫dy = ∫ (3x2 — 1) дх
у = х3 — х + С
Применение начального условия:
2 = (0)2 — 2 (0) + С
С = 2
Получается: f (х) = х3 — х + 2
Предлагаемые упражнения
Упражнение 1
- Найдите примитив f (x), удовлетворяющий начальным условиям:
- f » (х) = х; f ‘(3) = 1; f (2) = 5
- е » (х) = х + 1; f ‘(2) = 2; f (0) = 1
- f » (x) = 1; f ‘(2) = 3; f (1) = 10
- е » (х) = -х; f ‘(5) = 1; f (1) = -8
Упражнение 2.
- Воздушный шар, поднимающийся со скоростью 16 футов / с, сбрасывает мешок с песком с высоты 64 футов над уровнем земли.
- Определите время полета
- Что будет вектор VF когда я упаду на пол?
Упражнение 3.
- На рисунке показан график ускорения-времени автомобиля, движущегося в положительном направлении оси x. Автомобиль двигался с постоянной скоростью 54 км / ч, когда водитель нажал на тормоза и остановился за 10 секунд. Определите:
- Начальный разгон автомобиля
- Скорость автомобиля при t = 5с
- Смещение автомобиля при торможении
Упражнение 4.
- Определите примитивные функции с учетом производных и точки на графике:
- dy / dx = x, проходящий через точку (-1, 4)
- dy / dx = -x2 +1, который проходит через точку (0, 0)
- dy / dx = -x + 1, который проходит через точку (-2, 2)
Ссылки
- Интегральное исчисление. Неопределенный интеграл и методы интегрирования. Уилсон, Веласкес Бастидас. Университет Магдалены 2014
- Стюарт, Дж. (2001). Расчет переменной. Ранние трансцендентальные. Мексика: Thomson Learning.
- Хименес, Р. (2011). Математика VI. Интегральное исчисление. Мексика: Pearson Education.
- Физика И. Мак Гроу Хилл
From Wikipedia, the free encyclopedia
In calculus, the constant of integration, often denoted by 




More specifically, if a function 








Origin[edit]
The derivative of any constant function is zero. Once one has found one antiderivative 



Let 




To prove this, notice that ![[F(x)-G(x)]'=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf7a4d471877352525d86a56c595661d3061ae30)




Choose a real number 


thereby showing that 
Two facts are crucial in this proof. First, the real line is connected. If the real line were not connected, we would not always be able to integrate from our fixed a to any given x. For example, if we were to ask for functions defined on the union of intervals [0,1] and [2,3], and if a were 0, then it would not be possible to integrate from 0 to 3, because the function is not defined between 1 and 2. Here, there will be two constants, one for each connected component of the domain. In general, by replacing constants with locally constant functions, we can extend this theorem to disconnected domains. For example, there are two constants of integration for 

Second, 













For example, suppose one wants to find antiderivatives of 





It turns out that adding and subtracting constants is the only flexibility we have in finding different antiderivatives of the same function. That is, all antiderivatives are the same up to a constant. To express this fact for 
Replacing 




Necessity[edit]
At first glance, it may seem that the constant is unnecessary, since it can be set to zero. Furthermore, when evaluating definite integrals using the fundamental theorem of calculus, the constant will always cancel with itself.
However, trying to set the constant to zero does not always make sense. For example, 
So setting 
Another problem with setting 



This restriction can be rephrased in the language of differential equations. Finding an indefinite integral of a function 



There is another justification, coming from abstract algebra. The space of all (suitable) real-valued functions on the real numbers is a vector space, and the differential operator 


References[edit]
- ^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 0-495-01166-5.
- ^ Larson, Ron; Edwards, Bruce H. (2009). Calculus (9th ed.). Brooks/Cole. ISBN 0-547-16702-4.
- ^ «Definition of constant of integration | Dictionary.com». www.dictionary.com. Retrieved 2020-08-14.
- ^ Weisstein, Eric W. «Constant of Integration». mathworld.wolfram.com. Retrieved 2020-08-14.
- ^ «Reader Survey: log|x| + C«, Tom Leinster, The n-category Café, March 19, 2012
- ^
-
Download as E-Book -
Report an issue
Постоянная интегрирования
Функция с первообразной $F(x)$, имеет бесконечно много первообразных. По формуле:
$F(x)+C$
!
Запомните
постоянная интегрирования $C$, является произвольным настоящим числом ($Cinmathbb{R}$) и это очень важно для неопределенных интегралов.
i
Объяснение
Если взять производную, то константа $C$ исчезнет (правило константы).
Независимо от $C$, таким образом, все функции преобразуются в начальную функцию при взятии производной, которая соответствует определению первообразной.
Например
Установите три первообразных от $f(x)=x^2$.
- $F(x)=frac13x^3$, так как $F'(x)=x^2=f(x)$
- $F(x)=frac13x^3+2$, так как $F'(x)=x^2=f(x)$
- $F(x)=frac13x^3-4$, так как $F'(x)=x^2=f(x)$
i
Подсказка
Так как, постоянная интегрирования — это любое число, то добавим несколько констант интегрирования ($C_1+C_2+C_3=C$) в результате получается еще одно произвольное число, которое можно снова рассматривать как константу интегрирования.
Чтобы сэкономить бумагу, обычно добавляют $C$, но только в конце при расчете с помощью неопределенного интеграла.
Содержание:
- Формула
- Примеры вычисления интеграла константы
Формула
Интеграл константы равен произведению этой константы на переменную интегрирования плюс постоянная интегрирования.
Этот факт получается на основании
свойств неопределенного интеграла, а именно, что константу
можно выносить за знак интеграла и знак интеграла уничтожает знак дифференциала.
Примеры вычисления интеграла константы
Пример
Задание. Найти неопределенный интеграл $int 2dx$
Решение. Согласно формуле имеем, что
$$int 2 d x=2 x+C$$
Ответ. $int 2 d x=2 x+C$
Пример
Задание. Найти интеграл $int (pi — 1)dx$
Решение. Искомый интеграл равен
$$int(pi-1) d x=(pi-1) x+C$$
Ответ. $int(pi-1) d x=(pi-1) x+C$
Читать дальше: интеграл степенной функции.
И снова здравствуйте, друзья!
Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров. 
Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:
1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.
2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).
3) Таблица производных и правила дифференцирования.
Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. 
4) Методы интегрирования.
Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:
– метод подведения функции под знак дифференциала,
– метод замены переменной,
– метод интегрирования по частям.
О каждом из них — в отдельных уроках.
А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)
Прежде всего, это таблица интегралов:
Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):
Что ж, необходимая снаряга подготовлена. Пора в путь! 
Прямое применение таблицы
В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:
1) Смотрим в таблицу и ищем нужную формулу (формулы);
2) Применяем свойства линейности (где требуется);
3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!);
4) Записываем ответ.
Итак, поехали.)
Пример 1
Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:
Готово. 
Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.
Пример 2
Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. 
Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…
Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)
Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:
Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)
Следующий примерчик будет чуть покруче.
Пример 3
Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:
Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.
Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно «забиваем». 
А пока наш взор обращён на подынтегральную функцию
Не очень похоже на степенную функцию, но это она. 
А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:
В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:
Заменяем дроби степенями с отрицательными показателями;
Заменяем корни степенями с дробными показателями.
А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.
И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.
Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!
Пример 4
Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:
Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x-1.
Традиционная наша формула для первообразной степенной функции
здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:
Тогда, согласно этой формуле, первая дробь проинтегрируется так:
А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с «высоким» логарифмом:
Константа «а» в этой формуле равна двойке: a=2.
Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…)
Например, после первого интегрирования я должен был бы написать:
После второго интегрирования:
Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:
С1-С2
И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой «С». Вот так:
С1-С2 = С
Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:
Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)
Запоминаем:
При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.
Следующий пример тоже с дробью. Для разминки.)
Пример 5
В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:
Это самая последняя, восьмая формула. С арктангенсом. 
Вот эта:
И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х2 никакого коэффициента нету, а у нас — девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)
А новая дробь — уже нужная нам табличная функция под номером 8! Здесь а2=4/9. Или а=2/3.
Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:
Вот такой ответ. Этот пример, с коэффициентом перед х2, я специально так подобрал. Чтобы ясно было, что делать в таких случаях. 
Например:
Здесь а2 = 5, поэтому само «а» будет «корень из пяти». В общем, вы поняли.)
А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:
Пример 6
В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с «длинным» логарифмом:
Число А у нас — пятёрка. Подставляем в формулу и получаем:
И все дела. Это ответ. Да-да, так просто!)
Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?
Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):
Всё честно. 
Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус. 
Например:
Важно! В случае минуса, на первом месте под корнем должно стоять именно х2, а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!
Пример 7
Под корнем снова минус, но х2 с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:
А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а2!
Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:
И теперь пример решается в одно действие. 
Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…
Бонус:
В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.
В формуле №7
в знаменателе подынтегральной функции стоит разность квадратов х2 — а2. Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).
А вот в формуле №8
в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x2+a2 неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.
А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)
Пример 8
Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали. 
Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!
Да, (sin x)’ = cos x и (cos x)’ = —sin x.
Но!
Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:
Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.
Например, мы ещё со школы знаем, что производная синуса равна косинусу:
(sin x)’ = cos x.
Тогда для интеграла от того же синуса будет справедливо:
И всё.) С косинусом то же самое.
Исправляем теперь наш пример:
Предварительные элементарные преобразования подынтегральной функции
До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)
Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)
А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. 
Применение формул тригонометрии
Продолжим развлекаться с тригонометрией.
Пример 9
Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:
Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:
Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!
Смотрите:
А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:
И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.
А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. 
Пример 10
Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:
Вот и применяем эту формулу к нашей подынтегральной функции. В роли «альфа» у нас х/2.
Получаем:
Эффект потрясающий, правда?
Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)
Разберём ещё парочку типовых преобразований.
Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.
Обычные банальные школьные преобразования. Но порой только они и спасают, да.)
Пример 11
Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!
(x2 — 1)2(x2 + 1)2 = ((x2 — 1)(x2 + 1))2 = ((x2)2 — 12)2 = (x4 — 1)2 = x8 — 2x4 + 1
А теперь считаем:
И все дела.)
Пример 12
Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:
Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)
Интегрируем сумму степенных функций. По табличке.)
Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:
то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.
Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)
В некоторых случаях преобразования в дробях ещё более хитрые.
Пример 13
А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x2 в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс! 
И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):
Ну, что тут можно сказать? Вау!
Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.
Пример 14
Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:
Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби — один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.
Подытожим сегодняшний урок.
Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.
Несколько практических советов.
1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе — одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.
2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества:
Может очень крупно повезти. А может и нет…
3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
(a-b)(a+b) = a2-b2
и так далее…
4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.
Ну что, друзья? Я вижу, интегралы вам начинают нравиться. 
Что? Не знаете, как интегрировать арксинус/арккосинус? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)
Ответы (в беспорядке):
Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!
А у меня на сегодня всё. Успехов!


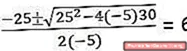



![{displaystyle {begin{aligned}{frac {d}{dx}}[sin(x)+C]&={frac {d}{dx}}sin(x)+{frac {d}{dx}}C\&=cos(x)+0\&=cos(x)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a1f94e2f3c827cbd77d0648f1d7532f57f3a35)