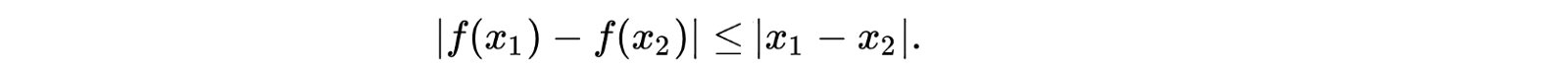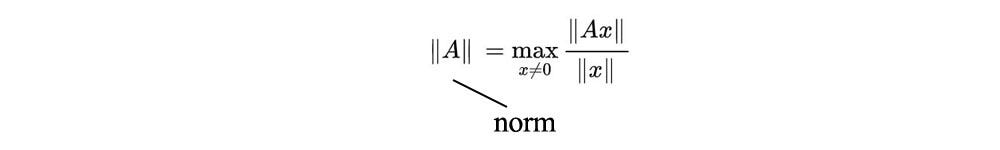Как найти константу липшица

From Wikipedia, the free encyclopedia

In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the Lipschitz constant of the function (and is related to the modulus of uniform continuity). For instance, every function that is defined on an interval and has bounded first derivative is Lipschitz continuous.^[1]

In the theory of differential equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to an initial value problem. A special type of Lipschitz continuity, called contraction, is used in the Banach fixed-point theorem.^[2]

We have the following chain of strict inclusions for functions over a closed and bounded non-trivial interval of the real line:

Continuously differentiable ⊂ Lipschitz continuous ⊂ -Hölder continuous,

where . We also have

Lipschitz continuous ⊂ absolutely continuous ⊂ uniformly continuous.

Definitions[edit]

Given two metric spaces (X, d_X) and (Y, d_Y), where d_X denotes the metric on the set X and d_Y is the metric on set Y, a function f : X → Y is called Lipschitz continuous if there exists a real constant K ≥ 0 such that, for all x₁ and x₂ in X,

^[3]

Any such K is referred to as a Lipschitz constant for the function f and f may also be referred to as K-Lipschitz. The smallest constant is sometimes called the (best) Lipschitz constant^[4] of f or the dilation or dilatation^{[5]: p. 9, Definition 1.4.1 [6][7]} of f. If K = 1 the function is called a short map, and if 0 ≤ K < 1 and f maps a metric space to itself, the function is called a contraction.

In particular, a real-valued function f : R → R is called Lipschitz continuous if there exists a positive real constant K such that, for all real x₁ and x₂,

In this case, Y is the set of real numbers R with the standard metric d_Y(y₁, y₂) = |y₁ − y₂|, and X is a subset of R.

In general, the inequality is (trivially) satisfied if x₁ = x₂. Otherwise, one can equivalently define a function to be Lipschitz continuous if and only if there exists a constant K ≥ 0 such that, for all x₁ ≠ x₂,

For real-valued functions of several real variables, this holds if and only if the absolute value of the slopes of all secant lines are bounded by K. The set of lines of slope K passing through a point on the graph of the function forms a circular cone, and a function is Lipschitz if and only if the graph of the function everywhere lies completely outside of this cone (see figure).

A function is called locally Lipschitz continuous if for every x in X there exists a neighborhood U of x such that f restricted to U is Lipschitz continuous. Equivalently, if X is a locally compact metric space, then f is locally Lipschitz if and only if it is Lipschitz continuous on every compact subset of X. In spaces that are not locally compact, this is a necessary but not a sufficient condition.

More generally, a function f defined on X is said to be Hölder continuous or to satisfy a Hölder condition of order α > 0 on X if there exists a constant M ≥ 0 such that

for all x and y in X. Sometimes a Hölder condition of order α is also called a uniform Lipschitz condition of order α > 0.

For a real number K ≥ 1, if

then f is called K-bilipschitz (also written K-bi-Lipschitz). We say f is bilipschitz or bi-Lipschitz to mean there exists such a K. A bilipschitz mapping is injective, and is in fact a homeomorphism onto its image. A bilipschitz function is the same thing as an injective Lipschitz function whose inverse function is also Lipschitz.

Examples[edit]

Lipschitz continuous functions that are everywhere differentiable

• The function defined for all real numbers is Lipschitz continuous with the Lipschitz constant K = 1, because it is everywhere differentiable and the absolute value of the derivative is bounded above by 1. See the first property listed below under «Properties».
• Likewise, the sine function is Lipschitz continuous because its derivative, the cosine function, is bounded above by 1 in absolute value.

Lipschitz continuous functions that are not everywhere differentiable

• The function defined on the reals is Lipschitz continuous with the Lipschitz constant equal to 1, by the reverse triangle inequality. More generally, a norm on a vector space is Lipschitz continuous with respect to the associated metric, with the Lipschitz constant equal to 1.

Lipschitz continuous functions that are everywhere differentiable but not continuously differentiable

Continuous functions that are not (globally) Lipschitz continuous

• The function f(x) = √x defined on [0, 1] is not Lipschitz continuous. This function becomes infinitely steep as x approaches 0 since its derivative becomes infinite. However, it is uniformly continuous,^[8] and both Hölder continuous of class C^{0, α} for α ≤ 1/2 and also absolutely continuous on [0, 1] (both of which imply the former).

Differentiable functions that are not (locally) Lipschitz continuous

• The function f defined by f(0) = 0 and f(x) = x^3/2sin(1/x) for 0<x≤1 gives an example of a function that is differentiable on a compact set while not locally Lipschitz because its derivative function is not bounded. See also the first property below.

Analytic functions that are not (globally) Lipschitz continuous

• The exponential function becomes arbitrarily steep as x → ∞, and therefore is not globally Lipschitz continuous, despite being an analytic function.
• The function f(x) = x² with domain all real numbers is not Lipschitz continuous. This function becomes arbitrarily steep as x approaches infinity. It is however locally Lipschitz continuous.

Properties[edit]

• An everywhere differentiable function g : R → R is Lipschitz continuous (with K = sup |g′(x)|) if and only if it has bounded first derivative; one direction follows from the mean value theorem. In particular, any continuously differentiable function is locally Lipschitz, as continuous functions are locally bounded so its gradient is locally bounded as well.
• A Lipschitz function g : R → R is absolutely continuous and therefore is differentiable almost everywhere, that is, differentiable at every point outside a set of Lebesgue measure zero. Its derivative is essentially bounded in magnitude by the Lipschitz constant, and for a < b, the difference g(b) − g(a) is equal to the integral of the derivative g′ on the interval [a, b].
  • Conversely, if f : I → R is absolutely continuous and thus differentiable almost everywhere, and satisfies |f′(x)| ≤ K for almost all x in I, then f is Lipschitz continuous with Lipschitz constant at most K.
  • More generally, Rademacher’s theorem extends the differentiability result to Lipschitz mappings between Euclidean spaces: a Lipschitz map f : U → R^m, where U is an open set in Rⁿ, is almost everywhere differentiable. Moreover, if K is the best Lipschitz constant of f, then whenever the total derivative Df exists.^{[citation needed]}
• For a differentiable Lipschitz map the inequality holds for the best Lipschitz constant of . If the domain is convex then in fact .^{[further explanation needed]}
• Suppose that {f_n} is a sequence of Lipschitz continuous mappings between two metric spaces, and that all f_n have Lipschitz constant bounded by some K. If f_n converges to a mapping f uniformly, then f is also Lipschitz, with Lipschitz constant bounded by the same K. In particular, this implies that the set of real-valued functions on a compact metric space with a particular bound for the Lipschitz constant is a closed and convex subset of the Banach space of continuous functions. This result does not hold for sequences in which the functions may have unbounded Lipschitz constants, however. In fact, the space of all Lipschitz functions on a compact metric space is a subalgebra of the Banach space of continuous functions, and thus dense in it, an elementary consequence of the Stone–Weierstrass theorem (or as a consequence of Weierstrass approximation theorem, because every polynomial is locally Lipschitz continuous).
• Every Lipschitz continuous map is uniformly continuous, and hence a fortiori continuous. More generally, a set of functions with bounded Lipschitz constant forms an equicontinuous set. The Arzelà–Ascoli theorem implies that if {f_n} is a uniformly bounded sequence of functions with bounded Lipschitz constant, then it has a convergent subsequence. By the result of the previous paragraph, the limit function is also Lipschitz, with the same bound for the Lipschitz constant. In particular the set of all real-valued Lipschitz functions on a compact metric space X having Lipschitz constant ≤ K  is a locally compact convex subset of the Banach space C(X).
• For a family of Lipschitz continuous functions f_α with common constant, the function (and ) is Lipschitz continuous as well, with the same Lipschitz constant, provided it assumes a finite value at least at a point.
• If U is a subset of the metric space M and f : U → R is a Lipschitz continuous function, there always exist Lipschitz continuous maps M → R which extend f and have the same Lipschitz constant as f (see also Kirszbraun theorem). An extension is provided by

where k is a Lipschitz constant for f on U.

Lipschitz manifolds[edit]

A Lipschitz structure on a topological manifold is defined using an atlas of charts whose transition maps are bilipschitz; this is possible because bilipschitz maps form a pseudogroup. Such a structure allows one to define locally Lipschitz maps between such manifolds, similarly to how one defines smooth maps between smooth manifolds: if M and N are Lipschitz manifolds, then a function is locally Lipschitz if and only if for every pair of coordinate charts and , where U and V are open sets in the corresponding Euclidean spaces, the composition

is locally Lipschitz. This definition does not rely on defining a metric on M or N.^[9]

This structure is intermediate between that of a piecewise-linear manifold and a topological manifold: a PL structure gives rise to a unique Lipschitz structure.^[10] While Lipschitz manifolds are closely related to topological manifolds, Rademacher’s theorem allows one to do analysis, yielding various applications.^[9]

One-sided Lipschitz[edit]

Let F(x) be an upper semi-continuous function of x, and that F(x) is a closed, convex set for all x. Then F is one-sided Lipschitz^[11] if

for some C and for all x₁ and x₂.

It is possible that the function F could have a very large Lipschitz constant but a moderately sized, or even negative, one-sided Lipschitz constant. For example, the function

has Lipschitz constant K = 50 and a one-sided Lipschitz constant C = 0. An example which is one-sided Lipschitz but not Lipschitz continuous is F(x) = e^−x, with C = 0.

See also[edit]

References[edit]

Сообщения без ответов | Активные темы

Автор	Сообщение
	Заголовок сообщения: Методы нахождения константы Липшица Добавлено: 01 фев 2011, 23:41
Начинающий Зарегистрирован: 14 сен 2010, 08:04 Сообщений: 22 Cпасибо сказано: 0 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Люди добрые, прошу Вас дать мне совет, посоветоваться, помочь, Какие существуют методы нахождения Липшицевой функции, и константы Липпшица. Прошу Вас помочь. Препод сказал, что существует литература нахождения константы Липшица и Липшицевой функции. И я не знаю , где искать. Помогите, пожалуйста. Очень Вас прошу.
Вернуться к началу

Prokop	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 02 фев 2011, 10:00
	Странный вопрос. Функция называется функцией Липшица в ограниченной области [math]Omega[/math], если она удовлетворяет условию Липшица. Условие Липшица состоит в том, что должно выполняться неравенство [math]|f(x)-f(y)|leqslant L|x-y|[/math] для всех [math]x,y in Omega[/math], [math]|x|[/math] — норма, [math]L[/math] — константа, которую называют константой Липшица. Если функция дифференцируема, то [math]Lleqslantsup|f'(x)|[/math] В общем случае, найти константу Липшица для конкретной функции — это работа.
Вернуться к началу

fara	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 02 фев 2011, 10:40
	Спасибо большое за ответ. Дано ду 1 порядка. Нужно найти константу липщица, чтобы сразу определить область, где будет находиться решение (диффур не решаем). То ли препод меня путает, то ли что….
Вернуться к началу

fara	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 02 фев 2011, 20:56
	Например, задача такая. Найти константу Липшица для [math]f(x,y)[/math] [math]f(x,y)=xy^2, x in [0,1], y’=f(x,y)[/math] Как видно из этой задачи , нужно найти константу Липшица, то есть область существования решения. И я Вас очень прошу помочь, какие методы оценки Липшица существуют, чтобы определить область, где решения находятся. Может литературу какую-н посоветуйте. Так как я не знаю….. Помогите, пожалуйста. Спасибо за внимание.
Вернуться к началу

Prokop	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 02 фев 2011, 22:18
	Условие Липшица по переменной [math]y[/math] требуется для единственности решения задачи Коши. Посмотрите книгу Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. (там уже на 23 стр. об этом говорится). Для Вашего уравнения областью существования и единственности решения задачи Коши является прямоугольник вида [math][0,1]times(-K,K)[/math], где [math]K>0[/math] — произвольное число. В самом деле по теореме Пеано надо доказать, что на этом множестве выполняется условие Липшица по переменной [math]y[/math]. Оценим разность [math]|f(x,y_2)-f(x,y_1)|=x,|y_2^2-y_1^2|=x,|y_2+y_1|cdot|y_2-y_1|leqslant2Kcdot|y_2-y_1|[/math] Так получаем требуемое неравенство на прямоугольнике.
Вернуться к началу

fara	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 04 фев 2011, 23:39
	Prokop, спасибо Вам огромное за заботу. Вы, очевидно, вычисляли по правилу треугольника? Просто мне надо прогу создать, чтобы находила липшевую константу. И я прошу методы, которые позволяют это сделать. Короче моя цель найти K из [math]|f(x,y+Delta y)-f(x,y)|<=K|Delta y|[/math] то есть в интерпретации нашего уравнения, получаем [math]|x(y+Delta)^2-xy^2|=x|(Delta y)^2|leqslantldots[/math] Дальше не знаю, помогите, пожалуйста…( не знаю чем [math]Delta y[/math] ограничен, как найти…, чем он ограничен.) Спасибо огромное за помощь….
Вернуться к началу

fara	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 05 фев 2011, 18:58
	Цитата: 1.Класс функций — правых частей. Под этим понимается: как задаются области определения и сами функции (аналитически, таблично и т.п.) Функции [math]y'(s)=f(s,y(s)), y(0)=C[/math] Функции задаются аналитически, область определения функции -отрезок [math][0,1][/math] Функции непрерывные, гладкие. Цитата: 2. Точность вычислений (нельзя же перебрать все точки) -задаем e сами, допустим. Цитата: 3. Формулировка самой задачи. Как можно, не решая дифференциальное уравнение, найти область, в которой будет находиться решение. Это мне нужно определения области D. Код: 3. Форма вывода результатов задачи. Поставляем в порядковый отрезок, в радиус сходимости. Чтобы проверить, удовлетворяет ли начальное приближение к уравнению. Мы находим приближения к точному решению. Остановка метода либо по точности, либо по итерации. То есть решаем диффур итерационным методом. Помогите, я правда не знаю…… Что делать!!!!! Вопрос, какие методы нахождения константы Липшица существуют?
Вернуться к началу

Prokop	Заголовок сообщения: Re: Методы нахождения константы Липшица Добавлено: 05 фев 2011, 20:40
	1. Функция [math]fleft( {x,y} right)[/math] — функция 2-х переменных. Какая область изменения по переменной [math]y[/math]? В примере [math]y in left( { — infty ,infty } right)[/math]. Если функция гладкая по переменной [math]y[/math], то для оценки константы Липшица на всей области достаточно найти оценку для частной производной функции по переменной [math]y[/math]. Так, например. в Вашем примере [math]fleft( {x,y} right) = xy^2[/math] и [math]left| {frac{{partial fleft( {x,y} right)}}{{partial y}}} right| = left| {2xy} right| leqslant 2left| y right|[/math] при [math]0<x<1[/math]. Если мы рассматриваем область, ограниченную по переменной [math]y[/math], [math]left| y right| leqslant K[/math], то константа Липшица не превосходит [math]2K[/math]. 3. Что такое область нахождения решения? Есть понятие области существования и единственности решения задачи Коши. Конец Вашего поста я совершенно не понял. В качестве метода нахождения константы Липшица для гладкой функции можно взять нахождение максимума модуля частной производной по переменной [math]y[/math].
Вернуться к началу

Пример 1.8. Доказать, что из выпуклости функции f (x) на отрезке [a, b]

следует ее унимодальность на [a, b] , если ограничиваться только

Применение некоторых методов одномерной минимизации возможно только в том случае, если скорость изменения целевой функции f (x) на любых участках отрезка [a, b] ограничена некоторым числом, одним и тем же для всех участков. В

этом случае говорят, что f (x) удовлетворяет на отрезке [a, b] условию Липшица.

Целевые функции большинства практических задач оптимизации таким свойством обладают.

1.Если неравенство (1.7) выполняется с константой L , то оно справедливо и для всех L′ > L . Поэтому для функции, удовлетворяющей условию Липшица, существует бесконечное множество констант L из (1.7). При использовании алгоритмов минимизации, включающих L как параметр, наилучшие результаты достигаются, как правило, если в качестве L берется минимальная из констант Липшица.

2.Из условия (1.7) сразу следует непрерывность f (x) на отрезке [a, b] .

Поэтому, согласно теореме Вейерштрасса, функция f (x) , удовлетворяющая на отрезке [a, b] условию Липшица, имеет на нем хотя бы одну точку минимума, хотя не является, вообще говоря, унимодальной.

14

3. Условие (1.7) означает, что модуль углового коэффициента любой хорды графика f (x) не превосходит L . Переходя в (1.7) к пределу при x′− x′′ → 0 ,

убеждаемся, что если в некоторой точке существует касательная к графику f (x) , то

k=1,1

1,6

5

4. Если функция f (x) имеет на отрезке [a, b] непрерывную производную, то

15

1.6. Классическая минимизация функции одной переменной

Из математического анализа известны следующие условия локального экстремума функции f (x) , дифференцируемой достаточное количество раз.

1.Если функция f (x) дифференцируема в точке ~x и достигает в ней локального экстремума, то f ′(~x ) = 0 (необходимое условие экстремума).

2.Пусть функция f (x) n раз дифференцируема в точке ~x и в этой точке все

(достаточные условия экстремума).

16

Перечисленные условия позволяют предложить следующий путь решения задачи минимизации (1.5):

1. с помощью условия 1 находим все точки возможного экстремума функции f (x) на интервале (a, b) , т.е. корни уравнения

(стационарные точки функции f (x) , принадлежащие интервалу (a,b) );

2.найденные стационарные точки исследуем в соответствии с условием 2, выделяя из них только точки локальных минимумов f (x) ;

3.значения f (x) в точках локальных минимумов и на концах отрезка [a, b]

сравниваем между собой. Наименьшему из этих значений соответствует точка глобального минимума f (x) на [a, b] .

Применение условия 2 требует вычисления высших производных функции f (x) , поэтому в большинстве случаев бывает проще сравнить значения f (x) во

всех стационарных точках, не интересуясь их характером. С учетом этого можно

■

17

GAN уязвим для коллапса режима и нестабильности обучения. В этой статье мы рассмотрим спектральную нормализацию для решения этих проблем. Однако, чтобы понять спектральную нормализацию, нам нужно сначала рассмотреть WGAN. Обсуждение будет включать математические концепции, с которыми люди могут не быть знакомы. Сначала мы представим условия, а позже сделаем их доступными.

Теоретически, когда сгенерированное распределение в GAN и реальное распределение не пересекаются, градиент функции стоимости будет состоять из областей исчезнувшего и взрывающегося градиента — красная линия ниже.

WGAN утверждает, что расстояние Вассерштейна будет лучшей функцией затрат, поскольку оно имеет более плавный градиент (синяя линия) для лучшего обучения. На практике при правильной настройке ванильный GAN может генерировать высококачественные изображения, но коллапс режима остается важной проблемой. И настоящая проблема для расстояния Вассерштейна состоит в том, как его эффективно вычислить. Одна из возможностей — применить ограничение Липшица для вычисления расстояния Вассерштейна. WGAN применяет простое отсечение для обеспечения ограничения 1-Липшица. WGAN-GP применяет ограничение с помощью более сложной схемы для исправления некоторых из наблюдаемых проблем в WGAN (подробности о WGAN и WGAN-GP можно найти здесь).

Спектральная нормализация — это нормализация веса, которая стабилизирует тренировку дискриминатора. Он управляет константой Липшица дискриминатора, чтобы смягчить проблему взрывающегося градиента и проблему коллапса режима. Этот подход будет менее вычислительным по сравнению с WGAN-GP и обеспечит хорошее покрытие режима.

Расстояние землеройного (EM) / метрическая система Вассерштейна

Давайте кратко рассмотрим расстояние Вассерштейна. Во-первых, мы хотим переместить 6 прямоугольников слева внизу в места справа, отмеченные пунктирным квадратом. Для блока №1 переместим его из позиции 1 в позицию 7. Стоимость перемещения определяется как расстояние перемещения. Таким образом, чтобы переместить ящик №1 в ячейку 7, стоимость равна 6.

Однако есть несколько способов переместить эти поля. Назовем план перемещения i γ ᵢ. Например, в первом плане γ₁ ниже мы перемещаем 2 ящика из местоположения 1 в местоположение 10. Ниже мы показываем два разных плана, стоимость перемещения каждого из которых составляет 42.

Однако не все транспортные планы имеют одинаковую стоимость. Расстояние Вассерштайна (или расстояние EM) — это стоимость самого дешевого транспортного плана. В приведенном ниже примере расстояние Вассерштейна (минимальная стоимость) равно двум.

Формализация расстояния Вассерштейна может быть легко расширена с дискретного пространства на непрерывное как:

Вернемся еще раз к нашему примеру. Каждая ячейка таблицы (x, y) ниже соответствует количеству блоков, перемещающихся из позиции x в y. После нормализации значения ячейки до значения вероятности стоимость перемещения для γ ₁ вычисляется как:

Расстояние Вассерштейна находит расстояние для самого дешевого плана.

Для любого действующего плана γ его поля должны равняться p (x) и p (y ) соответственно.

Например,

В непрерывном пространстве

∏ — это наборы действительных планов, поля которых равны p (x) и p (y). соответственно. γ — один из этих планов, который моделирует совместное распределение вероятностей для x и y. Мы хотим найти в ∏ тот, который имеет самую низкую стоимость.

Теперь давайте рассмотрим ограничение Липшица.

Липшицева преемственность

Действительная функция f: R → R является липшицевой, если

для ∀ реальных значений x ₁ и x ₂. Интуитивно понятно, что непрерывная функция Липшица ограничивает скорость изменения f.

Если мы соединим вместе f (x ₁) и f (x ₂), его наклон будет иметь абсолютное значение всегда меньше, чем K, который называется константой Липшица функции. Если функция имеет ограниченные первые производные, она липшицева.

Его константа Липшица равна максимальной абсолютной величине производных.

Для функции sin модуль ее производной всегда ограничен 1, и поэтому она липшицева. Постоянная Липшица равна единице. Интуитивно, непрерывность Липшица ограничивает градиенты и полезна для смягчения градиентных взрывов в глубоком обучении.

Графически мы можем построить двойной конус с наклоном K и — K. Если мы переместим его начало по графу, граф всегда останется вне конуса.

Расстояние Вассерштайна

Первоначальная формулировка расстояния Вассерштейна обычно неразрешима. К счастью, используя двойственность Канторовича-Рубинштейна, мы можем упростить расчет из

to

где sup — наименьшая верхняя граница. Нам нужно найти f, который является 1-липшицевой функцией, которая следует ограничению

и максимизирует

В следующих нескольких разделах мы попытаемся дать высокоуровневое доказательство без утомительных математических терминов. Но эти разделы не являются обязательными для чтения.

Двойная проблема (необязательно)

Давайте изучим проблему двойственности в контексте линейной алгебры. В оптимизации мы можем связать двойную проблему с основной проблемой.

Согласно теореме слабой двойственности, z (cᵀx) является нижней границей v (z ≤ v). Таким образом, двойственная задача устанавливает верхнюю оценку прямой задачи.

Сильная двойственность утверждает, что оптимальное решение прямой и двойственной задач одинаково (z * = v *). Однако эта сильная двойственность верна только для специальных условий. Задачи оптимизации, которые можно представить в виде линейной алгебры, действительно обладают сильной двойственностью (доказательство). Итак, если первичную задачу решить сложно, мы проверяем, может ли дуал быть проще. Это приводит к двойственности Канторовича-Рубинштейна.

Двойственность Канторовича-Рубинштейна (необязательно)

Итак, давайте применим это к нахождению расстояния Вассерштейна. Наша основная и двойная проблема будет в форме:

Первичный

с участием

Это сложно решить, и давайте попробуем вместо этого решить двойственную,

с участием

Целью является максимальное увеличение f ᵀ P r + g ᵀ P g при сохранении ограничения f ( xᵢ) + g (xⱼ) ≤ D ᵢⱼ.

Поскольку P r и P g неотрицательны, имеет смысл выбрать максимально возможное значение для g для максимизации цели , т.е. g = -f вместо g ‹- f. Без дополнительных доказательств мы обычно хотим g = -f. Наши ограничения становятся

То есть мы хотим ограничить изменение скорости нашей функции. Следовательно, чтобы решить двойственную задачу, нам нужно, чтобы f было липшицевым ограничением.

WGAN

Чтобы найти расстояние Вассерштейна, мы максимизируем двойственную задачу с ограничением, что f является 1-липшицевым.

Термин P r f и P g f становится ожидаемым значением для f (x), взятым из распределения P r и P g соответственно.

Графически мы хотим, чтобы f имел высокое значение, если P r ≥ Pg (P θ ниже) и низкое значение, если P g ›P r.

В GAN мы обучаем дискриминатор и генератор с функциями стоимости, указанными ниже.

В WGAN мы обучаем функцию Липшица f.

Мы оптимизируем w критика f с помощью расстояния Вассерштейна, используя цель.

Чтобы обеспечить соблюдение ограничения Липшица, WGAN просто обрезает значение w.

Алгоритм WGAN

Вот алгоритм WGAN.

Однако, как указано в исследовательской статье:

Отсечение веса — явно ужасный способ наложить ограничение Липшица. Если параметр отсечения большой, то может потребоваться много времени, чтобы любые веса достигли своего предела, что затрудняет обучение критика до оптимальности. Если отсечение небольшое, это может легко привести к исчезновению градиентов при большом количестве слоев… и мы застряли на отсечении веса из-за его простоты и уже хорошей производительности.

Настроить значение c сложно. Найти правильное значение сложно. Небольшое изменение может значительно изменить норму градиента. Кроме того, некоторые исследователи полагают, что улучшение качества изображения в WGAN обходится дорого за разнообразие режимов. WGAN-GP вводит штраф за градиент, чтобы обеспечить соблюдение ограничения Липшица. Однако это увеличивает сложность вычислений.

Спектральная норма

Норма матрицы или спектральная норма определяется как:

По сути, он измеряет, насколько матрица A может растянуть вектор x.

Согласно СВД, матрицу можно разложить как:

куда

U и V выбраны как ортогональные (UᵀU = I) собственные векторы AAᵀ и AᵀA соответственно. И AAᵀ, и AᵀA имеют одинаковые положительные собственные значения. S содержит квадратный корень из этих собственных значений, который называется сингулярными значениями.

Спектральная норма σ (A) — это максимальное сингулярное значение матрицы A (доказательство).

Спектральная нормализация

Давайте построим глубокую сеть со следующей формулировкой.

Для каждого слоя L выводится y = Ax, за которым следует функция активации a, скажем, ReLU.

Константа Липшица (или норма Липшица) функции g может быть вычислена с ее производной как:

Константа Липшица для g = Ax — это спектральная норма W.

Константа Липшица для RELU равна 1, так как ее максимальный наклон равен единице.

Следовательно, константа Липшица для всей глубокой сети f равна

Спектральная нормализация нормализует вес для каждого слоя со спектральной нормой σ (W), так что константа Липшица для каждого слоя, а также всей сети равна единице.

С помощью спектральной нормализации мы можем перенормировать вес всякий раз, когда он обновляется. Это создает сеть, которая смягчает проблемы градиентного взрыва. Но как мы можем вычислить σ (W) эффективно, ведь поиск собственных векторов обходится дорого.

Итерация мощности

k степень A с собственным вектором u довольно легко вычислить.

Мы можем выразить вектор v в линейную комбинацию собственных векторов A и легко вычислить его k -ю степень с помощью A.

Рассмотрим u как собственные векторы A. Мы можем переупорядочить эти собственные векторы так, чтобы u₁ был собственным вектором с наивысшим собственным значением (доминирующим собственным вектором). Вектор b можно разложить на собственные векторы A. Подойдет k -я степень A с v:

Начиная с b₀ с использованием следующей итерации, b сходится к кратному доминирующему собственному вектору. Короче говоря, мы можем начать со случайного вектора b₀. Умножая его на A, мы можем аппроксимировать доминантный собственный вектор.

Та же концепция может быть реализована с помощью итеративного вычисления u и v следующим образом (где A теперь записывается как W).

В SGD изменение W невелико на каждой итерации. Следовательно, изменение спектральной нормы также невелико. Следовательно, спектральная нормализация может повторно использовать значение u из предыдущей итерации. Действительно, вместо того, чтобы выполнять несколько итераций в степенной итерации, требуется только одна итерация, т.е. мы вычисляем уравнения 20 и 21, приведенные ниже, только один раз за обновление. Это значительно снижает вычислительную сложность. Вот последний алгоритм применения спектральной нормализации.

Мысли

Документ о спектральной нормализации предлагает математический анализ эффективности этого метода нормализации по сравнению с другими в разделах 2.3, 3 и приложениях D, E и F. Его нелегко понять, но я рекомендую людям прочитать его, если вы хотите его изучить. подробнее.

Источники и ссылки

Спектральная нормализация для генеративных состязательных сетей

Вассерштейн ГАН и двойственность Канторовича-Рубинштейна

Степенной метод аппроксимации собственных значений

спектральная нормализация стала проще

Что такое функции Липшица?

Названная в честь Рудольфа Липшица, функция называется k-липшицевой, если ее первые производные ограничены некоторой константой k. Минимальное значение для такого k называется константой Липшица функции. Такая функция имеет интересные свойства, среди которых:

Это означает, что если x1 и x2 близки друг к другу, то их прогнозы f (x1) и f (x2) также будут близкими. Поскольку нейронные сети приближают функции, мы сосредоточимся на 1-липшицевых сетях.

Почему константа Липшица сетей имеет значение

Такие сети находят множество применений в современном машинном обучении: доказано, что они устойчивы к злоумышленникам [1].

Состязательная атака — это нахождение x2 (изображения гиббона), близкого к нашему исходному x1 (изображение панды), так что их прогнозы f (x1) и f (x2) отличается. Основная проблема заключается в том, что добавленный шум при построении такого состязательного примера очень мал. Управление константой Липшица сети оказывает большое влияние на надежность противостояния: чем ниже константа Липшица, тем больше шума требуется для построения состязательного примера. Не стесняйтесь видеть это мягкое введение в состязательную надежность, чтобы узнать больше по этой теме.

Но это не единственное использование сетей Липшица: они также используются при оценке расстояния Вассерштейна. Метрика Вассерштейна позволяет измерить расстояние между двумя распределениями. Вычисление этой метрики требует оптимизации 1-липшицевых сетей. Это особенно используется в Wasserstein-GAN [2].

Различные уровни ограничений Липшица

Предыдущее уравнение говорит нам, что градиент нашей функции не более равен 1. Но применение этого ограничения не обязательно означает, что градиент фактически достигнет 1 в какой-то момент.

В зависимости от варианта использования нам могут потребоваться разные уровни липшицевых ограничений:

• «Мягкое» ограничение 1-Липшица: мы заставляем функцию градиента быть близкой к единице и равной единице в среднем. В этом случае градиент может быть больше единицы в некоторых конкретных точках входной области. Использование таких ограничений во время обучения не гарантирует, что конечные сети будут 1-липшицевыми, но позволяют упорядочить обучение.
• «Жесткое» ограничение 1-Липшица: принуждение градиента быть меньше или равным единице в каждой точке входной области. В некоторых точках градиент может быть меньше единицы. Это используется при борьбе с надежностью противостояния.
• «Градиент, равный единице почти везде»: заставляет градиент быть равным 1 почти везде. Этот конкретный класс сетей не подходит для традиционного машинного обучения. Однако это необходимо при работе с оценкой расстояния Вассерштейна [3].

Мы сосредоточимся на последних двух уровнях ограничений.

Как мы применяем эти ограничения к нейронным сетям

Известно, что вычисление константы Липшица нейронной сети является NP-трудной задачей. Однако было предложено несколько методов для обеспечения соблюдения таких «жестких» ограничений во время обучения. Большинство этих методов основаны на ограничении константы Липшица для каждого слоя, и затем можно использовать следующее свойство композиции:

Для линейных слоев, таких как плотные слои, есть множество способов достижения этого свойства, например, ограничение веса или нормализация.

Теперь мы рассмотрим существующие методы для плотных слоев. Напомним определение плотного слоя как линейного оператора, состоящего из нелинейной функции активации:

Сначала мы сосредоточимся на линейном ядре K. Позже мы увидим, как включить функции активации и как распространить эти методы на другие типы слоев.

Отсечение веса

Это наивный метод обеспечения ограничения Липшица на уровне каждого линейного слоя. Например, плотный слой с m входами и n выходами является 1-липшицевым, если все веса отсекаются в пределах следующего интервала:

Этого достаточно, чтобы гарантировать, что константа Липшица слоя меньше 1. Однако на практике градиент для точек обучающих данных обычно намного меньше 1. Это потому, что единственный способ иметь градиент, равный 1 в некоторых Дело в том, чтобы установить для всех весов их значения отсечения, что очень ограничительно. Другими словами, это означает, что сети, обученные при таких ограничениях, имеют константу Липшица меньше 1, но многие 1-липшицевы сети не удовлетворяют этому ограничению.

Можем ли мы тогда найти ограничение без таких недостатков?

Спектральная нормализация

Этот метод устраняет ограничения ограничения веса за счет использования спектральной нормализации. Математически этот тип нормализации основан на разложении по сингулярным числам:

Поскольку центральная матрица диагональна, и поскольку U и V не влияют на градиент K, тогда мы можем сказать, что градиент K ограничен:

Если мы разделим все веса на наибольшее значение сигмы, градиент будет ограничен единицей:

Такая нормализация дает очень сильные гарантии:

• Градиент не может быть больше 1.
• Во входной области существует такой набор точек, что градиент будет равен 1.

Более того, наибольшее сингулярное значение может быть быстро вычислено с помощью метода степенных итераций [4].

Он также предоставляет формальный способ выразить ограничение «градиент почти везде равен 1»:

Это ограничение также может быть получено на практике с помощью алгоритма ортонормировки Бьорка [5]

А как насчет функций активации?

Чтобы получить 1-липшицевую нейронную сеть, используемые функции активации также должны быть 1-липшицевыми. Большинство из них уже являются 1-липшицевыми: ReLU ELU, sigmoid, tanh, logSigmoid… Некоторые из них должны быть правильно параметризованы, например, leakyRelu, PReLU… наконец, некоторые вообще не являются 1-липшицевыми.

А как насчет других слоев?

Применение свойства композиции к слоям требует, чтобы каждый слой соблюдал ограничение 1-Липшица. Мы показали примеры нормализации для плотных слоев, но применимо ли это к любому типу слоя?

Слои свертки: кто-то может подумать, что нормализации ядра сверточного слоя (путем отсечения или спектральной нормализации) достаточно, но есть загвоздка: слои свертки используют заполнение, шаг, расширение … Все эти операции влияют на норму вывода, тем самым изменяя константу Липшица слоя. Чтобы поймать это явление, можно рассчитать поправочный коэффициент с учетом этих параметров [6].

Объединение слоев. Эти слои можно рассматривать как частный случай сверток, поэтому мы также можем применить поправочный коэффициент.

Норма пакетной обработки: при изменении масштаба этот уровень не ограничен. Кроме того, обучение с ограничением 1-липшица снижает потребность в таких слоях. Его использование было бы полезно только для исправления смещения, возникающего после каждого слоя, что также можно сделать, установив параметр use_bias для каждого слоя.

Исключение: он позволяет своего рода регуляризацию, переключая на нулевую часть выходных данных слоя. Однако при выводе применяется масштабный коэффициент для компенсации коэффициента отсева, который нарушает свойство Липшица.

k-липшицевские нейронные сети стали проще с DEEL-LIP

DEEL-LIP — это библиотека, построенная на Tensorflow, которая расширяет обычные элементы Keras, такие как слои, инициализаторы или активации, позволяя пользователю легко создавать 1-липшицевы сети. Предусмотренные слои используют спектральную нормализацию и / или ортонормировку Бьорка. При необходимости рассчитывается и применяется соответствующий поправочный коэффициент.

Как это использовать?

Во-первых, библиотеку можно установить с помощью pip

Теперь следующий код демонстрирует, как построить и скомпилировать нейронные сети с DEEL-LIP. Он очень похож на стандартный код Keras.

DEEL-LIP был разработан, чтобы быть простым в использовании для пользователей Keras:

• DEEL-LIP следует той же структуре пакета, что и Tensorflow / Keras.
• Все элементы (слои, активации, инициализаторы…) совместимы со стандартными элементами Keras.
• Когда слой переопределяет стандартный элемент Keras, он реализует тот же интерфейс с теми же параметрами. Единственное отличие заключается в параметре, который контролирует постоянную Липшица слоя.

Что важно при работе со слоями Липшица?

Поскольку константа Липшица сети является произведением констант каждого слоя, каждый отдельный слой должен соблюдать ограничение Липшица. Добавление одного слоя, который не удовлетворяет ограничению Липшица, достаточно, чтобы нарушить ограничение Липшица для всей сети.

Для удобства использования любой слой, импортированный из DEEL-LIP, безопасен: если вы можете импортировать его, вы можете его использовать. Это также верно для параметров слоев: неправильные настройки (например, нарушение ограничения Липшица) на слое вызовут ошибку.

Полный список доступных слоев можно найти в документации.

Каковы накладные расходы во время обратного распространения ошибки / вывода?

Во время обратного распространения ошибки нормализация весов добавляет накладные расходы на каждой итерации. Однако алгоритм спектральной нормализации добавляется непосредственно в график во время обратного распространения ошибки. Это называется дифференцируемым ограничением, которое дает гораздо более эффективные шаги оптимизации.

Во время вывода никаких накладных расходов не добавляется: нормализация обязательна только во время обратного распространения ошибки. DEEL-LIP предоставляет функцию экспорта, которую можно использовать для создания стандартной модели Keras из модели с глубокими губами. Затем каждый слой Dense или Conv2D преобразуется в стандартный слой Keras. Экспортируя модели, можно использовать сети, обученные с помощью DEEL-LIP, для вывода, даже не требуя установки DEEL-LIP.

Выводы

Липшицевы сети с ограничениями — это нейронные сети с ограниченными производными. У них есть много приложений, начиная от состязательной устойчивости и заканчивая оценкой расстояния Вассерштейна. Существуют различные способы обеспечения соблюдения таких ограничений. Спектральная нормализация и ортонормализация Бьорка являются одними из наиболее эффективных методов, библиотека DEEL-LIP обеспечивает простой способ обучения и использования этих ограниченных слоев.

Спасибо за прочтение!

использованная литература

[1] Мустафа Сиссе, Петр Бояновски, Эдуард Граве, Ян Дофин, Николя Усунье. Сети Парсевала: повышение устойчивости к примерам состязательности. ArXiv: 1704.08847 [stat.ML]
[2] Мартин Арджовски, Сумит Чинтала, Леон Ботту. Вассерштейн ГАН. ArXiv: 1701.07875 [stat.ML]
[3] Седрик Виллани. Оптимальный транспорт: старый и новый. Grundlehren der Mathematischen Wissenschaften. Springer Berlin Heidelberg, 2008.
[4] Википедия: метод степенных итераций
[5] Джем Анил, Джеймс Лукас, Роджер Гросс. Сортировка приближения функции Липшица. ArXiv: 1811.05381 [cs.LG]
[6] Матье Серрюрье, Франк Мамале, Альберто Гонсалес-Санс, Тибо Буассен, Жан-Мишель Лубес, Эустазио дель Баррио. Достижение надежности классификации с помощью оптимального транспорта с регуляризацией шарниров. ArXiv: 2006.06520 [cs.LG]