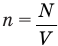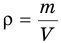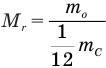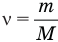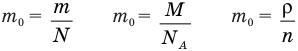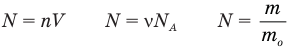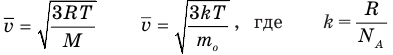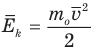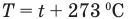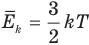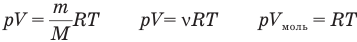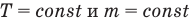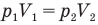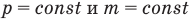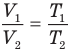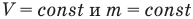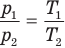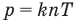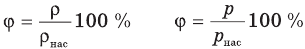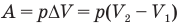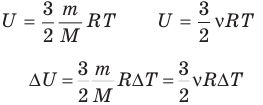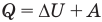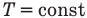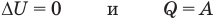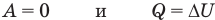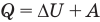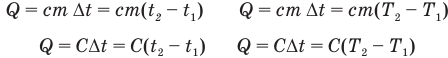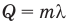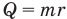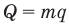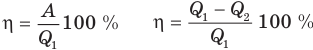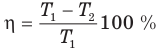Как найти концентрацию молекул газа через плотность - AvtoShod.ru

Формулы молекулярной физики

Формула концентрации молекул

Здесь n — концентрация , N — количество молекул (безразмерное), V — объем .

Формула плотности

Здесь — плотность вещества , m — масса вещества (кг), V — объем .

Формула относительной молекулярной массы

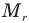
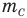
Здесь — относительная молекулярная масса (безразмерная), — масса одной молекулы (кг), — масса атома углерода (кг).

Формула количества вещества (количества молей)

Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).

Формулы массы одной молекулы

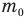
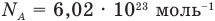
Здесь — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), — число Авогадро, — плотность вещества , n — концентрация молекул .

Формулы количества молекул

Здесь A — количество молекул (безразмерное), п — концентрация молекул , V— объем , v — количество вещества (количество молей) (моль), — число Авогадро , m — масса вещества (кг), — масса одной молекулы.

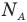
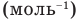
Формулы средней квадратичной скорости молекул

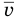
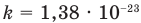
Здесь — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), Дж/К — постоянная Больцмана, — масса одной молекулы (кг).

Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па), — масса одной молекулы (кг), n — концентрация молекул , — средняя квадратичная скорость молекул (м/с), — средняя кинетическая энергия молекул (Дж).

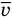
Формула средней кинетической энергии молекул

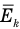
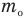
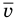
Здесь — средняя кинетическая энергия молекул (Дж), — масса одной молекулы (кг), — средняя квадратичная скорость молекул (м/с).

Связь шкал Цельсия и Кельвина

Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.

Связь средней кинетической энергии молекул идеального газа с абсолютной температурой

Здесь — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).

У равнение состояния идеального газа — уравнение Клапейрона — Менделеева

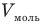
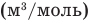
Здесь р — давление газа (Па), V — объем , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), — объем моля .

Объединенный газовый закон — уравнение Клапейрона

при

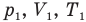
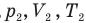
Здесь — давление (Па), объем и абсолютная температура (К) газа в первом состоянии, — давление (Па), объем и абсолютная температура (К) газа во втором состоянии.

Закон Бойля — Мариотта (изотермический процесс)

при

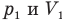
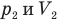
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), — давление (Па) и объем газа в первом состоянии, — давление (Па) и объем газа во втором состоянии.

Закон Гей-Люссака (изобарный процесс)

при

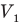
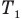
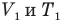
Здесь р — давление газа (Па), m — масса газа (кг), и — объем и абсолютная температура (К) газа в первом состоянии, — объем и абсолютная температура (К) газа во втором состоянии.

Закон Шарля

при

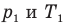
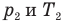
Здесь V — объем газа , m — масса газа (кг), — давление (Па) и абсолютная температура (К) газа в первом состоянии, — давление (Па) и абсолютная температура (К) газа во втором состоянии.

Связь давления идеального газа с концентрацией его молекул и температурой

Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа , абсолютная температура Т (К).

Формулы относительной влажности

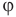
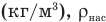
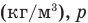
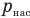
Здесь — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре — плотность насыщенного водяного пара при той же температуре — давление водяного пара в воздухе при данной температуре (Па), — давление насыщенного водяного пара в воздухе при той же температуре (Па).

Работа при изобарном изменении объема газа

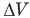
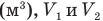
Здесь А — работа (Дж), р — давление газа (Па), — изменение объема газа — соответственно начальный и конечный объемы газа .

Внутренняя энергия идеального одноатомного газа

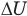
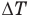
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), — изменение внутренней энергии (Дж), — изменение температуры (К).

Первый закон термодинамики

Здесь Q — количество теплоты, переданное термодинамической системе (Дж), — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)

Применение первого закона термодинамики к термодинамическим процессам

к изотермическому: при

к изохорному: при V = const

к изобарному: при р = const

к адиабатному: при Q = 0

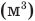
Здесь Т — абсолютная температура (К), — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем , р — давление (Па).

Формулы количества теплоты при нагревании или охлаждении тел

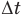
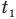
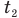
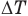
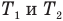
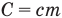
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), — изменение температуры тела по шкале Цельсия, и — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, — изменение абсолютной температуры тела (К), — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), — теплоемкость тела (Дж/К).

Формула количества теплоты при плавлении или кристаллизации

Здесь Q — количество теплоты (Дж), т — масса тела (кг), 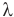— удельная теплота плавления вещества (Дж/кг).

Формула количества теплоты при парообразовании или конденсации

Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).

Формула количества теплоты при сгорании топлива

Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).

Коэффициент полезного действия теплового двигателя

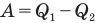
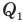
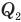
Здесь — коэффициент полезного действия (безразмерный или в %), — работа, совершенная двигателем (Дж), — количество теплоты, полученное рабочим веществом от нагревателя (Дж), — количество теплоты, отданное рабочим веществом холодильнику (Дж).

Коэффициент полезного действия идеального теплового двигателя

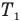
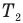
Здесь — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), — абсолютная температура нагревателя (К), — абсолютная температура холодильника(К).

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Источник

Смесь кислорода и азота
при температуре T = 290 K и давлении p = 5,8 кПа имеет плотность ρ = 0,40 кг/м³ .
Определите концентрацию молекул кислорода в смеси.

Решение.

Давление смеси газов,
согласно закону Дальтона, равно сумме парциальных давлений.

Эти давления найдем из
уравнения Клапейрона-Менделеева.

Где ρ₁ и ρ₂
– парциальные плотности кислорода и азота, т.е. плотности, которые имели бы
газы, если бы каждый из них отдельности занимал весь этот объем.

Так как из основного
уравления молекулярно-кинетической теории следует, что p
= nkT, уравнения (1) можно записать в следующем виде.

Подставим их в
равенство (2).

Концентрация молекул
смеси газов равна сумме концентрация компонентов.

Решая совместо
уравнения уравнения (3) и (4), находим концентрацию молекул кислорода.

Ответ: n₁ =
5,9•10²⁵ м^-3 .

Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.

Источник

Условие задачи:

Найти концентрацию молекул газа, у которого средняя квадратичная скорость молекул равна 500 м/с при температуре 300 К. Плотность газа 0,27 кг/м³.

Задача №4.1.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(upsilon_{кв}=500) м/с, (T=300) К, (rho=0,27) кг/м³, (n-?)

Решение задачи:

Запишем основное уравнение молекулярно-кинетической теории идеального газа:

[p = frac{1}{3}{m_0}nupsilon _{кв}^2]

Распишем в этой формуле концентрацию (n) как отношение числа молекул (N) к объему газа (V):

[p = frac{1}{3}frac{{{m_0}N}}{V}upsilon _{кв}^2]

По смыслу произведение (m_0N) равно массе газа (m), тогда:

[p = frac{1}{3}frac{m}{V}upsilon _{кв}^2]

Отношение массы газа (m) к объему газа (V) – это плотность газа (rho), поэтому:

[p = frac{1}{3}rho upsilon _{кв}^2;;;;(1)]

Также запишем формулу связи давления идеального газа (p) с концентрацией молекул газа (n) и абсолютной температурой (T):

[p = nkT;;;;(2)]

Приравняем формулы (1) и (2), далее выразим искомую концентрацию (n):

[frac{1}{3}rho upsilon _{кв}^2 = nkT]

[n = frac{{rho upsilon _{кв}^2}}{{3kT}}]

Произведем вычисления:

[n = frac{{0,27 cdot {{500}^2}}}{{3 cdot 1,38 cdot {{10}^{ – 23}} cdot 300}} = 5,43 cdot {10^{24}};м^{-3}]

Ответ: 5,43·10²⁴ м^-3.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.36 Энергия поступательного движения, которой обладают все молекулы газа, находящегося
4.1.38 В первом сосуде находится азот, во втором – водород. Чему равно отношение давления
4.1.39 В сосуде вместимостью 2 м3 находится 2,4 кг газа. Под каким давлением находится газ

Источник

Решение: давление смеси газов подчиняется закону Дальтона:

p = p₁ +p₂,

давление азота: p₁ = n₁kT, n₁ – искомая концентрация азота, давление водорода: p₂ = n₂kT, n₂ – искомая концентрация водорода, k = 1,38∙10^-23 Дж/К – постоянная Больцмана. Получаем:

p = (n₁ + n₂)kT . (1)

С другой стороны нам известна плотность смеси, которая равна:

[ rho =frac{{{m}_{1}}+{{m}_{2}}}{V}=frac{{{m}_{1}}}{V}+frac{{{m}_{2}}}{V}=rho {}_{1}+{{rho }_{2}}, ]

Плотность можно связать с концентрацией: концентрация – число частиц в единице объёма, умножив её на массу частицы (молекулы), мы получим массу единицы объема, т.е. плотность:

[ rho =ncdot {{m}_{0}}=ncdot frac{M}{{{N}_{a}}}, ]

M – молярная масса, N_a = 6,02∙10²³моль ^-1 – постоянная Авогадро. Получаем (2):

[ rho =frac{1}{{{N}_{a}}}left( n{}_{1}cdot {{M}_{1}}+{{n}_{2}}cdot {{M}_{2}} right), ]

Получили систему двух уравнений (1) и (2), решая их совместно, например получим так:

[ {{n}_{1}}=frac{p}{kT}-{{n}_{2}}, ]
[ {{n}_{2}}=frac{rho {{N}_{a}}-frac{p{{M}_{1}}}{kT}}{{{M}_{2}}-{{M}_{1}}}. ]

Ответ: n₁ = 2,55∙10²⁴, n₂ = 3,95∙10²⁵.

Источник

Основное уравнение молекулярно-кинетической теории:

где

– давление
газа,

– концентрация
молекул,
–
масса одной молекулы,

–
средняя квадратичная скорость одной
молекулы,
—
плотность газа,
–абсолютная
температура,

–
постоянная
Больцмана.

Средняя
кинетическая энергия поступательного
движения одной молекулы:

Изопроцессы
(газовые законы) –
для
:

1)
— изотермический:;

2)
—
изобарный:;

3)
—
изохорный:

Уравнение
Менделеева-Клапейрона:

где

–
объём газа,

– масса газа,

– молярная масса;
)
– универсальная
газовая постоянная.

Количество
вещества:

где

– общее число молекул;

– постоянная Авогадро.

Скорости
молекул:

—
средняя квадратичная,

—
средняя арифметическая,

—
наиболее вероятная.

Нормальные
условия:

—
объём
одного моля газа.

Примеры решения задач

Задача
1.
Смесь кислорода и азота при температуре
t=27⁰С
находится под давлением Р=2,3·10²Па.
Масса кислорода составляет 75% от общей
массы смеси. Определите концентрацию
молекул каждого из газов.

Дано:

Т=300
К;

Р=2,3·10²Па;

m₁=0,75
m;

М₁=0,032
кг/моль;

М₂=0,028
кг/моль.

Решение:

Смесь
газов принимаем за идеальный газ,
описываемый уравнением Менделеева–
Клапейрона:

,

(1)

где

—

(2) концентрация смеси газов;

–
концентрациямолекул
кислорода,
–
концентрация молекул

азота;–
постоянная Больцмана.

n₁— ?n₂— ?

Из
выражений (1) и (2) имеем:

.

(3)

Выразим
концентрацию n₁
через концентрацию n₂.

По
условию задачи масса кислорода:

m₁
= 0,75 m
,
(4)

где
m
– масса смеси.

Массу
кислорода можно выразить также через
концентрацию n₁
и объем газа:

m₁
=
,
(5)

где
М₁
–
молярная масса кислорода;
N_A
– число Авогадро;
V
– объем газа.

Приравняв
правые части выражений (4) и (5), получим:

.
(6)

Масса
азота m₂=0,25m,
или иначе
.
Приравняв значенияm₂
из последних двух формул, найдем:

.
(7)

Из
выражений (6) и (7) имеем:

.
(8)

Подставив
в формулу (3) значение n₂из
последнего выражения, получим n₁
=.
После подстановки значений и вычисленияn₁=
0,40·10²³
1/м³,
n₂=
0,15·10²³(1/м³).

Ответ:
n₁=
0,40·10²³
1/м³,
n₂=
0,15·10²³(1/м³).

Задача
2.
В
закрытом сосуде объемом V=1
м³находится
m₁=1кг
азота и m₂=1,5
кг воды. Определите давление в сосуде
при температуре t=600⁰С,
зная, что при этой температуре вся вода
превратится в пар.

Дано:

V=1
м³;

m₁=1
кг;

m₂=1,5
кг;

Т=873К;

M₁=0,028
кг/моль;

M₂=0,018
кг/моль.

Решение:

По
закону Дальтона давление в сосуде
после превращения воды в пар:

Р=Р₁+Р₂
, (1)

где
Р₁
— давление азота, Р₂
– давление водяного пара. Состояние
азота в сосуде определяется уравнением
Менделеева — Клапейрона:

(2)

где
M₁
– молярная масса азота, R
–
универсальная газовая постоянная.
Аналогично для водяного пара:

,
(3)

где
M₂
– молярная масса водяного пара.

Р
— ?

Из
уравнений (2) и (3) имеем:
,.
После подстановки давленийР₁
и
Р₂
в
выражение
(1)
имеем
Используя числовые значения, получим:

Р
=
8,62·10⁵Па.

Ответ:
Р =
8,62·10⁵Па.

Задача
3.
Определите
число молекул воздуха в аудитории
объемом V=180
м³
при температуре t=22⁰С
и давлении Р=0,98·10⁵
Па. Какова концентрация молекул воздуха
при этих условиях?

Дано:

V=180
м³;

Т=295
К;

Р=0,98·
10⁵
Па;

Решение:

Число
молей воздуха в аудитории:

(1)

где
– N_A
—
число Авогадро, m
– масса воздуха в аудитории, М
–
молярная масса воздуха.

Из
выражения (1):

N
=
.
(2)

N
— ? , n — ?

Число
молей воздуха в аудитории можно выразить,
используя уравнение Клапейрона-Менделеева

откудаПосле
подстановки
из последней формулы в выражение (2)
получим:

.
(3)

Используя
числовые значения, определим N
=
0,43·10²⁸.
Проверим единицы измерения правой части
выражения (3)
. Концентрацию (число молекул в единице
объема) определим по формуле:

.
После
подстановки:
n=0,24·10²⁶.

Ответ:
N =
0,43·10²⁸,
n=0,24·10²⁶.

Задача
4.
Определите
среднюю квадратичную скорость молекул
некоторого газа, плотность которого
при давлении Р=1,1·10⁵Па
равна ρ=0,024.
Какова масса одного моля этого газа,
если значениеплотности
дано для температуры 27⁰С?