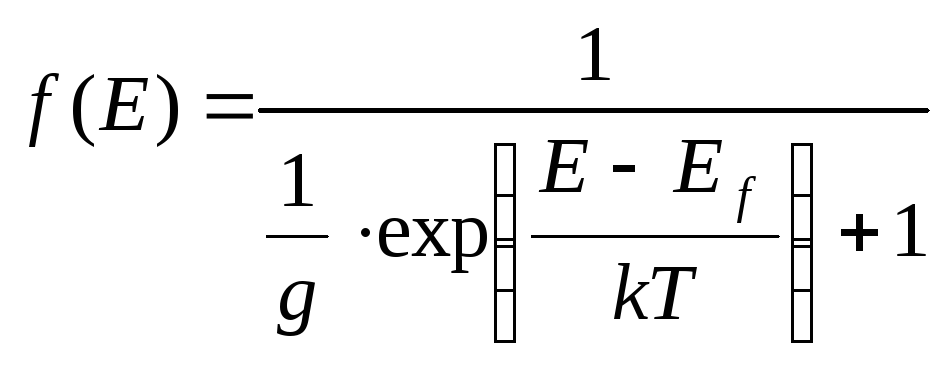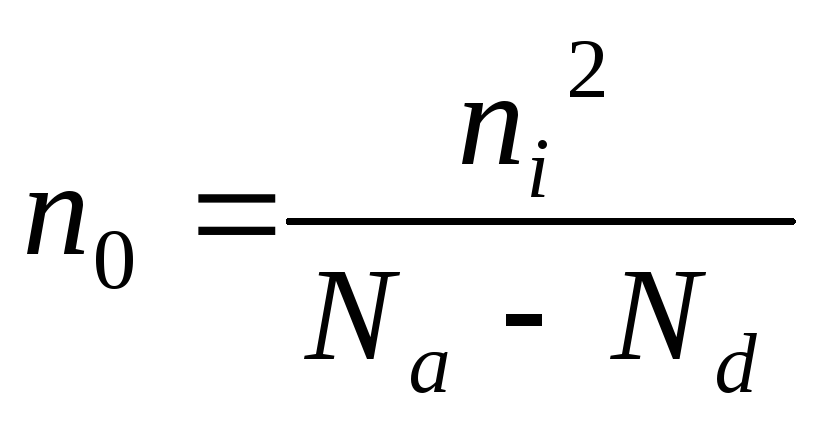Концентрация электронов и дырок в кремнии в состоянии термодинамического равновесия после легирования его атомами сурьмы
Страницы работы
Содержание работы
1 Постановка задачи
Определить концентрацию
электронов и дырок в кремнии в состоянии термодинамического равновесия после
легирования его атомами сурьмы с концентрацией м-3
. Определить концентрацию носителей после легирования атомами бора с
концетрацией м-3 при Т=300К.
2 Краткие
теоретические сведения
Концентрация свободных
электронов в зоне проводимости невырожденного примесного полупроводника определяется
выражением:
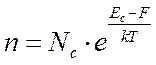
где — энергия уровня Ферми,
— энергия дна зоны проводимости,
— эффективная
плотность квантовых состояний в зоне проводимости.
Аналогично концентрация
свободных дырок в валентной зоне невырожденного примесного полупроводника будет
равняться:
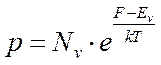
(2)
где —
эффективная плотность квантовых состояний в валентной зоне,
— энергия потолка валентной зоны,
— энергия уровня Ферми,
Энергию любого уровня
можно выразить через потенциал электрического поля:
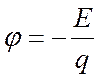
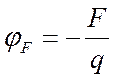
(3)
где — заряд электрона.
С учётом выражения (3)
формулы (1) и (2) можно переписать в виде:
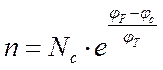
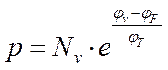
(5)
где —
температурный потенциал
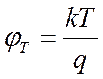
(6)
— потенциал уровня Ферми,
— потенциалы дна зоны проводимости и потолка валентной зоны
соответственно. Разница этих потенциалов равна ширине запрещённой зоны:
. (7)
Потенциал уровня Ферми
для невырожденного полупроводника определяется выражением:
для n-области:
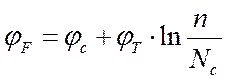
для p-области:
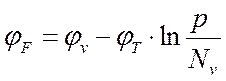
3 Математическое
моделирование для примесного полупроводника
3.1 Легирование кремния
атомами сурьмы
Валентность кремния 4,
валентность сурьмы 5, следовательно, сурьма является донором, Nд=м-3. Т. к.
сурьма донор, то полупроводник n-типа,
следовательно, основные носители заряда электроны, неосновные — дырки.
При Т=300К практически
все атомы примеси ионизированы, т. е. .
Концентрацию дырок можно
найти по выражению (5). Учитывая соотношения (7) и (8), получим:
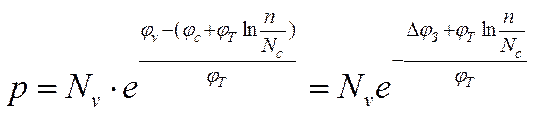
Исследуем данную
зависимость от температуры.
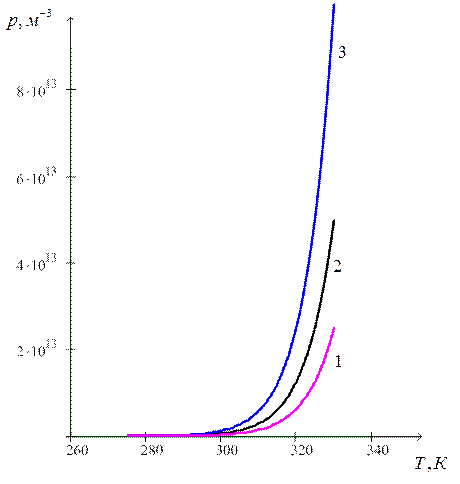
Рисунок-1 Зависимость концентрации неосновных
носителей(р) от температуры(Т) в кремнии
согласно формуле (10) после легирования его атомами сурьмы с концентрацией:1 – , 2 –
, 3 –
.
Вычислим
концентрацию дырок при Т=300К:
,
,
,
,
.
Получим:
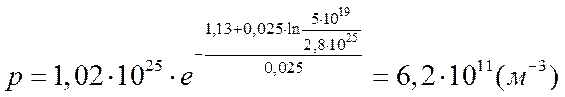
При легирование кремния
атомами сурьмы концентрация основных носителей(электронов) будет практически
постоянной и равной концентрации донорной примеси. Концентрация же неосновных
носителей(в данном случае, дырок) будет быстро возрастать с ростом температуры,
как видно из рис.1, но на несколько порядков отставать от основных. Причём чем
больше концентрация атомов сурьмы, тем меньше концентрация неосновных
носителей.
3.2 Легирование кремния
атомами бора
Валентность бора 3, бор
– акцепторная примесь, Nа =2*1018 м-3.
Т. к. бор – акцептор, то после легирования его атомами образца кремния получаем
полупроводник p-типа, где основные носители заряда
— дырки, неосновные — электроны.
При температуре Т=300К
практически все атомы примеси ионизированы, т. е. .
Концентрацию дырок можно
найти по выражению (4). Учитывая соотношения (7) и (9), получим:
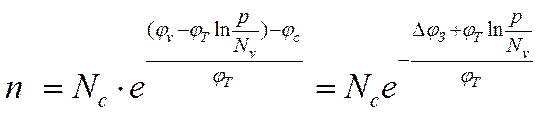
Исследуем данную
зависимость от температуры.
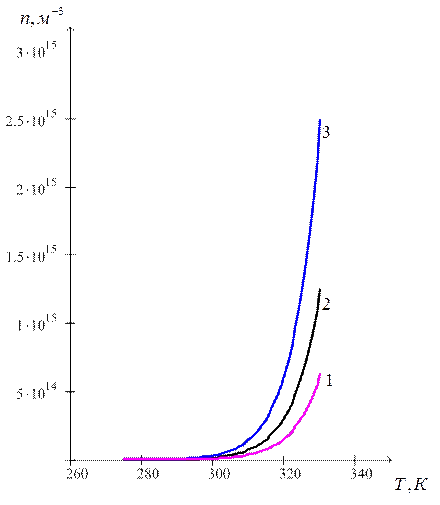
Рисунок-1 Зависимость концентрации неосновных
носителей(n) от температуры(Т) в кремнии согласно формуле (11) после легирования его атомами бора с
концентрацией:1 – , 2 –
, 3 –
.
Вычислим
концентрацию электронов при Т=300К:
,
,
,
,
.
Получим:
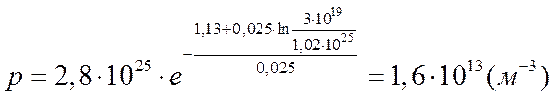
При легирование кремния
атомами бора концентрация основных носителей(дырок) будет практически
постоянной и равной концентрации акцепторной примеси. Концентрация же
неосновных носителей(в данном случае, электронов) будет быстро возрастать с
ростом температуры, как видно из рис.2, но на несколько порядков отставать от
основных. Причём чем больше концентрация атомов бора, тем меньше концентрация неосновных
носителей.
Похожие материалы
- Эффект резонанса, при котором прогрессирующе увеличивается напряжение
- Исследование однофазных выпрямителей в среде Multisim. Однофазный однополупериодный выпрямитель
- Схемотехнический уровень проектирования ЭС. Интегрированные библиотеки
Информация о работе
Тип:
Отчеты по лабораторным работам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
СЕМИНАР 1
Статистика
электронов и дырок
Единицы
измерения в системе СИ:
Основные: м кг с А К
Производные: Дж Вт Кл В Ом Ф
Дж = м*кг/с = A*B*c
= 1 Вт*с
1 Вт = 1 Дж/с 1 эВ = 1.6*10-19
Дж
φt
= k*T/e
= 25.8 мВ (при 300 К) = 4.14*10-21
Дж
1 мкм = 10-4
см = 10-6
м 1 нм = 10-7
см = 10-9
м
Приближенные
вычисления:
— ln
10 = 2.3 ln
1015
= 15*ln
10 = 15*2.3 = 34.5
— exp 1 = 2.718, exp 10 =
2.2*104,
exp 20 = 4.85*108
Физические
постоянные:
h
= 6.62*10-34
Дж*с k
= 1.38*10-23
Дж/К e
= 1.6*10-19 Кл
m
= 9.1*10-31
кг
ε0
= 8.86*10-14
Ф/см εε0
= 1.1 пФ/см (для Si)
εdε0
= 0.4 пФ/см (для SiO2)
Свойства полупроводников
|
п/п |
Eg, |
ni, |
Подвижность |
ε |
|
Si |
1.12 |
1.5*1010 |
1500 |
11.9 |
|
Ge |
0.66 |
2.5*1013 |
3900 / 1900 |
16 |
|
GaAs |
1.43 |
1.8*106 |
8500 / 400 |
10.9 |
|
Марка подложки |
Материал |
Проводимость |
Удельное |
Концентрация |
|
КДБ-10 |
Si |
дырочная |
10 |
Na |
|
КЭФ-4.5 |
Si |
электронная |
4.5 |
Nd |
Теоретические сведения
Зонная диаграмма полупроводника
Функция распределения Ферми-Дирака
g
– фактор вырождения примесного уровня;
g
=1 для собственного полупроводника,
g
= 2 для донорного примесного уровня
(электрон на одном уровне может иметь
два значения спина)
В полупроводнике выделяют следующие
концентрации:
— Nd
– полная концентрация донорной примеси,
Nd+
— концентрация ионизированных доноров
— Na
– полная концентрация
акцепторной примеси, Nа+
— концентрация ионизированных акцепторов
— n
– концентрация электронов,
— р – концентрация дырок
Справедливо уравнение
электронейтральности и формулы для
концентраций:
n0
+ Na—
= p0
+ Nd+
,
=
2.83*1019
см-3
(для Si,
300 К)
,
=
1.02*1019
см-3
(для Si,
300 К)
mc
= 1.08*m,
mv
= 0.56*m
— Закон действия масс для невырожденных
п/п
ЗАДАЧА 1
Для собственного полупроводника
найти вероятность заполнения электроном
уровня на дне Ес при T=0
и 300 К. Считать что при 300 К уровень Ферми
(Ef)
расположен по середине Еg
(E-Ef
= Eg/2)
Решение:
Используем функцию распределения
Ферми-Дирака
При расчете можно считать,
что энергия выражается в вольтах, а
вместо kT
использовать φt
= 25.8 мВ

1.86*10-10
ЗАДАЧА 2
Вычислить
положение уровня Ферми (Ef)
в собственном Si
при T=300K
Решение: В
собственном полупроводнике нет примесей.
Из уравнения электронейтральности
следует, что n
= p.
Используя формулы для концентраций:
ЗАДАЧА 3
Найти
концентрацию электронов и дырок в
кремнии при Т=300К, если концентрация
донорной примеси Nd
= 1016
cм-3,
Nа
= 0. Считать примесь полностью ионизованной.
Решение: Уравнение электронейтральности
при полной ионизации примеси имеет вид:
n0
+ Na
= p0
+ Nd
Из закона действия масс: p0
= ni2/n0
Составляем квадратное
уравнение: n02-(Nd-Na)*n0-ni2=0
Решение:

см-3 p0
= 2.25*104
см-3
МОЖНО СЧИТАТЬ, ЧТО ПРИ Nа
= 0: n0
= Nd,
p0
= ni2/Nd
ЗАДАЧА 4
Рассчитать концентрацию
электронов и дырок в кремнии с концентрацией
примеси Nа
= 1016
см-3,
Nd
= 3*1015
см-3,
Т=300 К
Решение:

см-3
n0
= ni2/Na
= 3.2*104
см-3
МОЖНО СЧИТАТЬ ЧТО:
ЗАДАЧА 5
Образец кремния n-типа
находится в состоянии термодинамического
равновесия при T=300K.
Параметры образца:
-
ρ = 5 Ом*см
-
μn
= 1600 μp
= 600 [см2/(В*с)] -
ni
=
1.4*1010
см-3,
Nc
= 1019
см-3 -
Ec
—
Ed
= 0.05 эВ
Найти:
-
Концентрацию электронов и дырок
-
Положение уровня Ферми
-
Вероятность того, что донорный уровень
занят или свободен
Решение:
-
ρ = 1/σ
-
σ = e(μn
n
+ μp
p) -
n*p
= ni2 -
σ
= e( μn
n +
μp
ni2/n
)

см-3
р = 2.5*105
см-3
2.
,
находим Ec-Ef
= 0.244 эВ
3. Так как Ec
— Ed
= 0.05 эВ, то Ed
— Ef
= 0.194 эВ и вероятность заполнения донорного
уровня определяется функцией распределения
Ферми-Дирака

ЗАДАЧА 6
Найти удельное сопротивление
(ρ) собственного Si
при 300 К.
Решение:
ρ
= 1/σ
σ
= e(μn
n +
μp
p) = e
μp
ni
(B+1)
B=μn
/ μp
=2.5
ρ
= 1.2 *106
Ом*см
Соседние файлы в папке SemTE
- #
- #
- #
- #
- #
- #
Определить концентрацию свободных электронов и дырок в чистом кремнии и указать положение уровня Ферми.






Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№1 Задача 159. Определить концентрацию свободных электронов и дырок в чистом кремнии и указать положение уровня Ферми.
Решение. Концентрацию носителей в собственном полупроводнике можно определить по формуле: , где – эффективная плотность состояний для электронов в зоне проводимости; где – эффективная плотность состояний для дырок в валентной
- Для плоскости, изображённой на рисунке, найти: 1) индексы Миллера; 2) направление нормали; 3) наименьшие отрезки, отсекаемые данной плоскостью на осях координат.
- Для плоскости, изображенной на рисунке, найти: 1) индексы Миллера; 2) направление нормали; 3) наименьшие отрезки, отсекаемые данной плоскостью на осях координат.
- Концентрация свободных электронов натрия 3∙1028 м-3. Найдите скорость электронов на уровне Ферми при абсолютном нуле температуры.
- Цезий имеет плотность ρ = 1,90∙103¬ кг/м3. Определить энергию Ферми в эВ у электронов проводимости цезия. Определить также среднюю кинетическую энергию электронов в предположении, что полная энергия Ферми в образце, содержащем N электронов, равна EF = N.
1.16, б). И для валентных электронов, чтобы переместится в зону проводимости, энергетические уровни вблизи нижней границы недоступны. Следовательно, электронам валентной зоны труднее перейти в зону проводимости и в результате в материале существует меньшее число дырок. И уровень Ферми у тт-полупроводника (уровень с вероятностью заполнения 1/2) сдвинут к зоне проводимости, показывая, что много энергетических уровней уже занято (заполнено) электронами доноров, и меньшее число дырок образовано в валентной зоне. Точно так же и в случае р-полупроводника электроны из валентной зоны заполняют акцепторные уровни. И в результате в материале мало электронов в зоне проводимости. Следовательно, в р-полупроводннках уровень Ферми сдвинут к валентной зоне (см.
рнс. 1.12, б). Как уровень Ферми зависит от температуры в и- и р-полупроводниках? Когда температура полупроводника увеличивается, число пар электрон — дырка, образованных за счет тепловой энергии, будет расти. При дальнейшем повышении температуры, число таких электронно-дырочных пар еще более увеличится и мажоритарная сущность электронов (в и-полупроводнике) и дырок (в р-полупроводнике) начнет исчезать, т. е. легированный полупроводник начнет смещаться в сторону собственного полупроводника. Следовательно, при повышении температуры уровень Ферми будет сдвигаться к середине запрещенной зоны (к положению уровня Ферми в собственном полупроводнике).
Это справедливо как для и-, так и для Р-полупроводников. Разумеется, температура не имеет значительного влияния на уровень Ферми в чистом (собственном) полупроводнике и он будет оставаться в середине запрещенной зоны. 1.9.
Заключение Квантованные энергетические уровни изолированных атомов приводят к зонной структуре в твердых телах. Зонная структура — ключ к пониманию электрических свойств вещества, и именно разница в зонных структурах металлов, полупроводников и диэлектриков обусловливает различные величины злектропроводности. Зонная структура полупроводников определяется существованием двух типов носителей заряда — дырок и электронов. Легируя полупроводники, можно управлять концентрацией электронов и дырок. Легирование — — это добавление рассчитанного количества известной примеси (легирующей добавки) в кристалл чистого полупроводника.
Легируя трехвалентными атомами (например, бора), можно создать дополнительные дырки в кремнии или германии, которые имеют по четыре валентных электрона. Атомы примеси внедряются в кристаллическую решетку, становятся отрицательными ионами и остаются в узлах кристаллической решетки исходного материала. Легирование не нарушает электрической нейтральности кристалла. Аналогично, при легировании кремния атомами с пятью электронами валентности (например бор) создаются дополнительные электроны.
Атомы примеси заменяют некоторые атомы кремния, каждый атом примеси отдает один дополнительный электрон и остается в виде положительного иона в узле кристаллической решетки полупроводника. Уровень Ферми является важным параметром и характеризует концентрацию носителей заряда в кристалле.
В чистом (собственном) полупроводнике уровень Ферми лежит в середине запрещенной зоны. Он смещается, оставаясь в запрещенной зоне при обычном легировании (не выРождающем полупроводник). Вод влиянием слабого и среднего электрического поля в полупроводнике свободные носители движутся с постоянной скоростью дрейфа. движение носителей под воздействием электрического поля выражается термином «подвижность», обозначаемой и и определяемой как скорость на единицу электрического поля.
На подвижность влияет рассеивание подвижных ~арядов при их взаимодействии с кристаллической решеткой. 2 — 2890 ~~~34 Глава 1. Введение в полупроводники Примеры Пример 1.1. Собственное удельное сопротивление германия при 300 К равно 50 Ом . см. Найти концентрацию собственных носителей в полупроводнике.
Подвижности электрона и дырки соответственно равны р„ = 3900 смэ/(В с), рр — — 1900 смэ/(В с). Решение. Удельная проводимость (о) или удельное сопротивление (р) полупроводника выражаются как и = 1/Р = упРо + ДРРр. В собственном полупроводнике и = р = пь Следовательно, = 1/Ре = упе(Р + Рв) или 1 и;— 2,1 1013 3, р; х д х (и„+рр) 50 х 1,6 х 10-1в(3900+1900) Пример 1.2. Чему равна концентрация доноров в и-германии с сопротивлением 2 Ом см? Подвижность электронов равна 4000 смэ/В с. Решение. Для и-полупроводника удельное сопротивление р найдем из равенства 1 — =о = упр„. Р Так как концентрация электронов и равна концентрации доноров Мо, имеем о 1 д?о— др„рдр„(2 х 1,6 х 10 — 1е х 4000) ‘ Мо = 7,8 х 10ы атомов/смв. Пример 1.3.
Найти концентрацию дырок и электронов в р-кремнии с удельным сопротивлением 120 Ом см. Подвижность дырок и электронов кремния рр — — 500 смэ/В с и р„= 1300 смэ/В с, а концентрация собственных носителей пв = 1 5 ‘ 1010 см-3 Решение.
Для р-Я! удельное сопротивление выражается как 1 — = опрр. Р Отсюда 1 1 р (рдр ) (120 х 1,6 х 10 — 1в х 500) или р~и10м см э пр .р зи) Концентрация электронов в р-о1 2 и = — ‘ = (1,5 х 10’е)~/10’~ = 2,2 х 10е см з; р п=22х10 см з. Пример 1.4. В кристалле и-Я (ширина запрещенной зоны = 1,1 эВ) уровень Ферми должен быть на 0,1 эВ ниже дна зоны проводимости. Концентрация собственных носителей пл = 1,5 10~с см з.
Найти концентрацию донора. Эффективные массы дырки и электрона принять равными. Решение. Для и-полупроводника положение уровня Ферми (Еу„) выражается как Еу„= ‘ » + (3/4) ЙТ 1п — ~ + — 1п Если т„= тр, имеем /Уп’1 Еу„= уровень Ферми собственного полупроводника+ яТ1п ~ — ( ~,( (в середине запрещенной зоны, Еу,). И далее имеем: Еу„— Еу; = МТ1п | — ), (Ел/2 — 0,1 эВ) = МТ1п ~ — ) . и, Так как ширина запрещенной зоны кремния равна 1,1 эВ, имеем 0,45 = яТ1п Подставляя МТ = с эВ при 300 К, получаем Мп =6,5 х10т х 1,5 х10’е = 9,7х10’7 10гз см з.
ПРимеР 1.5. Показать, что если для полупроводника при данной температуре концентрация электронов п будет равна и;(рр/р„)’~~, то его проводимость будет минимальна. Здесь п; — плотность собственных носителей, пр и р„— соответственно подвижность дырок и электронов. Решение. В общем виде проводимость полупроводника выражается как о = д(пр„+ ррт). Подставляя р = п~/и, полу ~аем ( 36 Глава 1. Введение в полупроводники Дифференцируя это равенство, получаем до/ди = о(рг + поир( — 1/и~)).
Проводимость будет минимальна при условии до/дп = О. Приравнивая выражение нулю, получаем искомый результат: и = и;(рр/и„) 7 . Пример 1.6. В кремнии концентрация собственных носителей и; = 10’в см з и концентрация донорной примеси АР~> = 10го см з.
Посредством инжекции в полупроводнике образованы дополнительные носители. Вычислить отношение концентрации дырок (р) к концентрации электронов (и) в точке, в которой плотность концентрации дополнительных носителей равна 10гв см з. Также оценить вызванное инжекцией увеличение р и п в процентах. Решение. Для и-полупроводника с АРр = 10го см з равновесная концентрация электронов по = 10го см з (потому что Агп = и). Равновесная концентрация дырок равна ро = пг/по = 10зг/10го = 10гг см з.
В условии задачи дано, что концентрация дополнительных носителей (как электронов, так и дырок) в результате инжекции стала равной 101в см з. Следовательно, в точке инжекции суммарная концентрация электронов становится п = 10го + 10зз = ПП х 10зз см — з Аналогично для концентрации дырок, 10гг + 101в 10гв см — з Получим отношение р/п = 0,01. Процент увеличения концентрации дырок (неосновных носителей) х100=, х100= —, х100=10з%, а процент увеличения концентрации электронов (основных носителей) ! — ~(101 х 10гз — 10″) 1 ~ х100= х100=0,01х100=1%.
по ~ ~ 10го Дополнительная литература по теме 1. Яее8ег В,. Яеппсопг(цсФог РЬув)св, Ярг)п8ег, 1982. 2. Яге Я.М. РЬувкв оГ Яеш(сопе1пс$ог 1)еч)сев, Ж11еу, 1981. 3. ВачЫ К. Реггу аш1 ЛопаФЬап Р. В1ге), Е1ес1гошс Ма$ег(а( апе( 11еч)сев, Асас1еппс Ргевв, 2001. 4. Япп1Ь В.А. Яеш(сове)пс1огв, СазпЬгЫ8е, 1978. Зд 373 ВОПРОСЫ 1.1. Как дырка проводит электрический ток? 1,2.
Какие свойства полупроводников ставят их в класс важнейших материалов для производства электронных приборов? 1.3. Какие различия в зонных структурах металлов, диэлектриков и полупроводников? 1.4. Чем объясняется уменыпение удельной проводимости полупроводника и удельного сопротивления металла с ростом температуры? 1.5. Как обосновать, что донорные уровни в полупроводнике и-типа расположены на доли электронвольта ниже зоны проводимости? 1.6. Нарисуйте график зависимости уровня Ферми в полупроводнике р-типа от температуры. Проанализируйте график. 1.?.
Концентрация неосновных носителей в р-полупроводнике падает ниже концентрации собственных носителей при той же температуре. Обсудите. 1.8. Характеристики р- или и-полупроводников при повышенных температу- рах (скажем, около 400К) близки к характеристикам нелегированного по- лупроводника. Объясните, почему. Задачи 1.1. На 10в атомов исходного материала — германия — добавили один атом мышьяка.
Сколько дырок и электронов стало доступно для проводимости при 300К? Концентрация собственных носителей германия при 300 К равна 2,5 х 101в см в (у Ое — 4,41 х 10ээ атомов в см з). Ответ: и = 4,41 х 10м см в, р = 1,42 х 10м см 1.2. Чему равна концентрация доноров в и-Ое с удельным сопротивлением 4 Ом см при 300 К? Подвижности носителей заряда р„= 4000 смэ/В с, рр = 2000 см~/В с.
Отвеин Яп = 3,9 х 10’~ см в. 1.3. Найдите концентрации дырок и электронов в р-кремнии с удельным сопротивлением 240 Ом см. Концентрации носителей заряда р .=- 500 смэ/В . с и рв = 1300 смэ/В с, концентрация собственных носителей и; = 1,5 х х101в см в. Ответ:р=бх10’всм вии=4,5х10 см в. 14 Удельное сопротивление образца кремния 50 Ом. см при 300 К. Рассчи таите концентрацию дырок, если кремний р-типа, и концентрацию электронов, если кремний и-типа. рр — — 500 смэ/В с и рв = 1300 смэ/В . с. Ошввт: концентрадая дырок = 2,5 х 10м см в; кояпентрвлия электронов = 10м см в. ~~( 38 Глава 1.
Введение е полупроводники 1.5. Покажите, что при заданной температуре, если концентрация дырок равна 1!э р=и; то проводимость полупроводника будет минимальна. 1.6. Требуется, чтобы в кристалле р-кремния уровень Ферми был расположен на 0,2 эВ выше валентной зоны. Рассчитайте требуемую концентрацию акцептора в материале.
Концентрация собственных носителей и; = 1,5 х х 10’о см э и ширина запрещенной зоны Яд — — 1,1 эВ. Примите эффективные массы электрона и дырки равными. Ответ: Хл = 1,8 х 10’в см в. 1.7. Кристалл германия имеет концентрацию собственных носителей и; = 10’э см е и концентрацию акцепторов ДРл = 101е см э. Процессом ннжекции в полупроводнике образованы дополнительные носители. Определить отношение концентрации электронов (и) к концентрации дырок (р) в точке, в которой плотность дополнительных носителей равна 101в см е.
Работа добавлена на сайт samzan.net: 2016-03-13
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
Задачи по полупроводникам
1. Вычислить собственную концентрацию носителей заряда в кремнии при T=300K, если ширина его запрещенной зоны Eg=1,12еВ, а эффективные массы носителей заряда mn=1,05m0, mp=0,56m0, где m0 – масса свободного электрона.
Решение.
Концентрация собственных носителей заряда рассчитывается по формуле:
где Nc – эффективная плотность состояний в зоне проводимости,
Nv – эффективная плотность состояний в валентной зоне.
Рассчитаем эффективные плотности: Nc=2,69·1019 см-3, Nv=1,05·1019 см-3.
Подставим эти значения в формулу концентрации собственных носителей заряда.
Ответ: ni=6.45·109 см-3, Nc=2,69·1019 см-3, Nv=1,05·1019 см-3.
2. Уровень Ферми в кремнии при 300 К расположен на 0,2 еВ ниже дна зоны проводимости. Рассчитайте равновесную концентрацию электронов и дырок в этом полупроводнике, если ширина его запрещенной зоны = 1,12 еВ, а эффективные массы носителей заряда mn=1,05m0, mp=0,56m0, где m0 – масса свободного электрона.
Решение.
Равновесная концентрация электронов в зоне проводимости:
По условию задачи Ec – EF = 0,2 эВ.
При помощи соотношения действующих масс ni2= np найдем равновесную концентрацию неосновных носителей заряда:
p= ni2/n
Произведем вычисления.
Ответ: Nc=2,69·1019 см-3, n = 1,17·1016 см-3, p = 3,55·103 см-3.
3. При исследовании температурной зависимости концентрации носителей заряда для чистого кремния в области собственной электропроводности получены следующие результаты: T1=463 К собственная концентрация ni1=1020 м-3, а при T2=781 К ni2=1023 м-3. Н основании этих данных рассчитать ширину запрещенной зоны при T=300 К, если коэффициент ее температурного изменения b=-2.84·10-4 эВ/К.
Решение.
Отношение концентраций при температурах T1 и T2 равна:
Eg = Δ — bT
Отсюда
Ответ: Δ = 2,0227 эВ, Eg = 2,1 эВ.
4. На сколько процентов изменится коэффициент диффузии электронов в невырожденном полупроводнике при повышении температуры на 10%, если подвижность электронов изменяется пропорционально Т-1,5.
Решение.
Коэффициент диффузии электронов вычисляется по формуле:
Преобразуем второе выражение с учетом соотношений:
T2 = 1,1T1
Найдем отношение второго коэффициента диффузии к первому и получим результат:
5. Образец собственного кремния имеет удельное сопротивление 2000 Омм при комнатной температуре и концентрацию электронов проводимости ni=1,4·1016 м-3. Определить удельное сопротивление образца легированного акцепторной примесью с концентрацией 1021 и 1023 м-3. Предположите, что подвижность дырок остается одинаковой как для собственного, так и для примесного кремния и равной μp= 0,25μn.
Решение.
Удельное сопротивление полупроводника обратно пропорционально электропроводности:
Из этой формулы найдем подвижность электронов.
μn= 0,178
μp= 0,25μn= 0,0445
Теперь найдем удельное сопротивление данного образца:
Ответ: μn= 0,178, μp= 0,0445, ρ1= 13,5 Ом·м.
6. Определить при какой концентрации примесей удельная проводимость при температуре 300 К имеет наименьшее значение. Найти отношение собственной удельной проводимости к минимальной при той же температуре. Собственная концентрация носителей при этой температуре ni= 2,1·1019 м-3, подвижность электронов μn= 0,39 м2/(В·с), подвижность дырок μp=0,19 м2/(В·с).
Решение.
Удельная проводимость выражается формулой:
Так как np = ni2 , следовательно,
Продифференцируем это выражение:
Это выражение имеет минимум при:
т.е. когда
или
тогда
Удельная проводимость у собственного полупроводника:
Минимальная удельная проводимость полупроводника:
Отношение собственной удельной проводимости к минимальной:
Концентрация дырок:
Ответ: σi =1,95 См/м, σ =1,83 См/м, σi /σ =1,07, p =3·1019 м-3.
7. Вычислить время жизни неосновных носителей заряда в полупроводнике, если их установившаяся концентрация при воздействии источника возбуждения составляет 1020 м-3, а начальная скорость уменьшения избыточной концентрации при отключении источника 7,1·1023 м-3 с-1. Найти избыточную концентрацию Δn через время t=2мс после выключения источника возбуждения.
Решение.
Зависимость концентрации избыточных носителей заряда от времени выражается соотношением:
Δn0 – избыточная концентрация носителей заряда в момент выключения источника возбуждения,
τ – время жизни носителей.
Продифференцируем по t:
где τn — время жизни неосновных носителей заряда. Начальная скорость при t=0 равна 7,1·1023 м-3 с-1:
Отсюда:
Избыточная концентрация через t=2с:
Ответ: τn = 140 мкс, Δn = 8,7·1019 м-3.
8. В толстом образце германия равномерно по объему генерируются электронно-дырочные пары. Найти скорость поверхностной рекомбинации, если концентрация неравновесных дырок на поверхности образца в 4 раза меньше, чем в объеме; Lp=0,2 см, τp=10-3 с.
Решение.
Запишем уравнение непрерывности:
Граничные условия таковы:
Решение уравнения имеет вид:
Из граничных условий C2 = 0.
Так что:
Найдем отношение полученных величин:
Откуда выведем скорость поверхностной рекомбинации:
Ответ: s = 600 см/с.