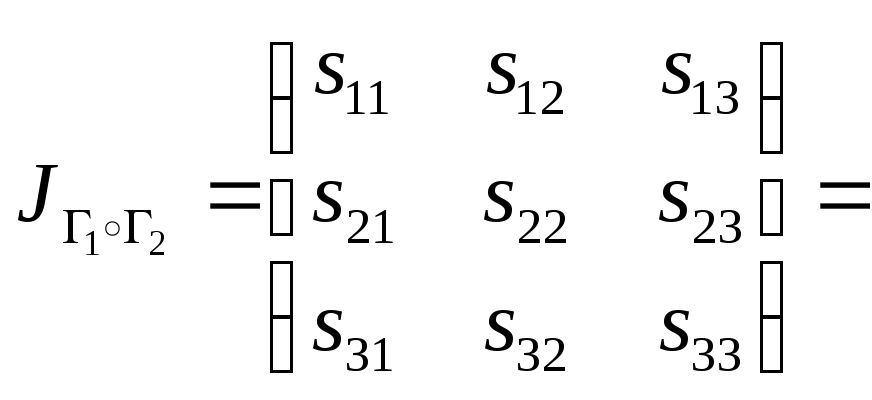
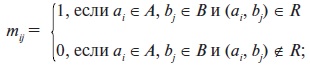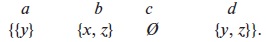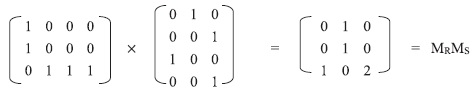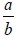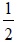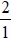Операции над соответствиями на множествах
Поскольку соответствия можно считать множествами, то все операции над множествами (пересечение, объединение, разность, дополнение и т.д.) можно применить и к соответствиям. Заметим, что, говоря о дополнении соответствия из в
, мы имеем в виду дополнение до универсального соответствия из
в
, т.е. до декартова произведения
. Естественно, что и равенство соответствий можно трактовать как равенство множеств.
В то же время на соответствия можно распространить операции, определяемые для отображений. Мы рассмотрим здесь две такие операции.
Композиция соответствии. Следуя аналогии с композицией отображнений, композицией (произведением) соответствий и
называют соответствие
(1.3)
Поясним построение композиции двух соответствий. Обратимся сначала к отображениям (как частным случаям соответствий). Пусть заданы отображения (возможно, частичные): из
в
и
из
в
. Композиция
определяется как отображение из
в
, задаваемое формулой
. Тем самым задается график отображения
, т.е. множество упорядоченных пар
, таких, что
. При этом упорядоченная пара
будет принадлежать графику отображения
, если и только если найдется элемент
, такой, что
и
. Таким образом, график композиции отображений
и
есть
(1.4)
Необходимо заметить, что запись означает
, т.е. отображения в композиции пишутся в порядке, обратном тому, в каком они применяются. Мы же будем везде использовать запись
, полагая, что
и порядок записи отображений в композиции совпадает с порядком их применения. Это обусловлено тем, что композиция отображений определяется нами как частный случай композиции соответствий, при записи которой естественным оказывается именно такой порядок.
Легко видеть, что (1.4) есть частный случай (1.3). Отметим, что при построении композиции отображений обычно предполагают, что пересечение области значений отображения и области определения отображения
не пусто
, поскольку в противном случае композиция была бы пуста. Для отображений, не являющихся частичными,
, так как
. Поэтому в данном случае пересечение
всегда не пусто.
Полезно отметить также, что если и
— биекции, то и композиция их тоже будет биекцией.
Вернемся к рассмотрению композиции соответствий . Полагая, что область определения
соответствия
не пуста, возьмем произвольный элемент
. Пусть сечение
соответствия
не пусто и найдется такой элемент
, что сечение
также не пусто. Тогда непустое множество
будет подмножеством сечения соответствия
в точке
. Сечением соответствия
в точке
будет непустое в силу сделанных предположений множество всех таких упорядоченных пар
, что
, а
для некоторого
. Говоря неформально, нужно перебрать все элементы
из сечения
. Таким образом, различие в построении композиции соответствий и композиции отображений заключается в том, что «промежуточный» элемент z в общем случае не единственный и каждому такому элементу также ставится в соответствие не единственный элемент
.
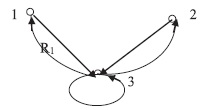
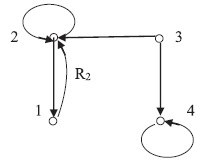
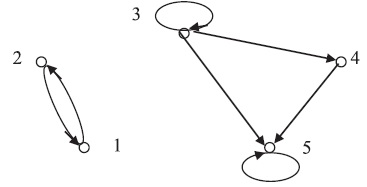
Пример 1.8. Соответствие возьмем из примера 1.3. Соответствие
зададим как соответствие из множества программ
в множество заказчиков программного обеспечения
. Пусть
Рассмотрим процесс построения композиции соответствий и
. Начнем с элемента
. Имеем
Отсюда получаем сечение композиции по элементу
Рассуждая аналогично, получим и
.
Построение графа композиции проиллюстрировано на рис. 1.3.
Отметим, что область определения композиции соответствий содержится в области определения первого соответствия, а область значений композиции соответствий — в области значений второго соответствия. Из приведенных рассуждений следует, что для того, чтобы композиция соответствий была отлична от пустого соответствия, необходимо и достаточно, чтобы пересечение области значений первого соответствия и области определения второго соответствия было не пусто.
К определению композиции соответствий можно подойти с более общих позиций. Пусть и
. При этом на множества
и
априори не накладывается никаких органичений. Композиция
соответствий
и
в этом случае также определяется соотношением (1.3). Чтобы такая композиция была отлична от пустого соответствия, необходимо и достаточно выполнение условия
. В частности,
всякий раз, когда
.
Пример 1.9. Рассмотрим соответствие из множества
в множество
и соответствие
из множества
в множество
. В данном случае
, но
, поскольку
Заметим, что композиция соответствий и
не коммутативна, т.е. в общем случае
, поскольку
, а
.
Композиция бинарного отношения на множестве
Бинарное отношение на множестве является частным случаем соответствия. Для двух бинарных отношении и
, заданных на множестве
, их композиция
(1.3) как соответствий является бинарным отношением на том же множестве
. В этом случае говорят о композиции бинарных отношений на множестве
.
Композицию бинарного отношения
на некотором множестве с самим собой называют квадратом бинарного отношения
и обозначают
.
Рассмотрим пример построения композиции бинарных отношений на множестве и покажем, что в общем случае для двух бинарных отношений и
также имеет место неравенство
, хотя обе композиции, в отличие от аналогичных композиций двух произвольных соответствий, заданы на одном и том же множестве.
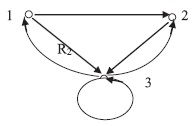
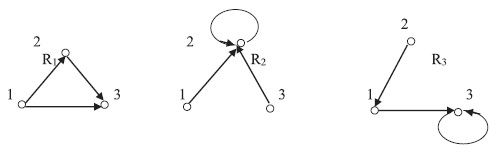
Пример 1.10. а. Зададим на множестве бинарные отношения
и найдем композицию
, если
.
Имеем и
. Следовательно,
. Далее
и
. Так как
, то в итоге получим
. Построение композиции проиллюстрировано на рис. 1.4,а.
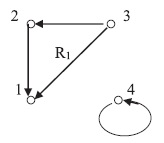
Найдем композицию . Поскольку
, а
, то
. Аналогично
, а
, поэтому
. Далее
, поэтому
, а
и
. Построение композиции проиллюстрировано на рис. 1.4,б.
Легко видеть, что .
б. Пусть отношение на множестве действительных чисел определено как функция
. Найдем квадрат этого отношения (линейной функции от одного переменного).
Согласно (1.4), это будет функция , такая, что
, то есть
. Это тоже линейная функция, но с другими коэффициентами.
Свойства композиции соответствий
Приведем некоторые свойства композиции соответствий:
1) ;
2) для любого соответствия имеет место
;
3) ;
4) для любого бинарного отношения на множестве имеет место равенство
.
Эти свойства нетрудно доказать методом двух включений. Рассмотрим в качестве примера доказательство свойства 3. Пусть некоторая упорядоченная пара принадлежит композиции
. Тогда, согласно (1.3), найдется такой элемент
, что
и
. Последнее означает, что
или
. Таким образом, для элемента
имеем
и
или
и
. Первая альтернатива имеет место при
, а вторая — при
, что означает
. Тем самым включение
доказано.
Доказательство включения запишем коротко, используя логическую символику:
В данном случае доказательства двух включений не совсем симметричны: элементы и
во второй части доказательства не обязаны совпадать.
Замечание 1.4. В тождестве, выражающем свойство 3, нельзя вместо объединения поставить пересечение, так как в этом случае тождество нарушатся. Можно доказать, что сохранится лишь включение
а обратное включение в общем случае не имеет места.
Анализ свойств 2 и 4 показывает, что роль пустого соответствия аналогична роли нуля при умножении чисел, а диагональ множества играет роль, аналогичную роли единицы, на множестве всех бинарных отношений на
.
Обратное соответствие и его свойства
Соответствие, обратное к соответствию , есть соответствие из
в
, обозначаемое
и равное, по определению,
.
Для соответствия из примера 1.3
Обратное соответствие обладает следующими легко проверяемыми свойствами:
1) ;
2) .
Для бинарного отношения на множестве
обратное соответствие есть бинарное отношение на том же множестве. В этом случае говорят о бинарном отношении
на множестве
, обратном к
.
Заметим, что соответствия и
в общем случае не совпадают. Даже для бинарного отношения
на множестве
, а также
и
.
Например, для бинарного отношения на множестве
графы самого отношения, обратного отношения
, композиций
и
представлены на рис. 1.5.
Если — отображение, то оно является соответствием. Обратное к
соответствие из
в
в общем случае не является отображением. Действительно, соответствие
, обратное к
, состоит из всех упорядоченных пар вида
. Поскольку в общем случае могут найтись такие два различных элемента
и
, что
, то соответствие
в общем случае не будет функционально по второй компоненте и поэтому не будет отображением. Если отображение
инъективно, то обратное соответствие есть частичное отображение из
в
. Если отображение
биективно, то обратное соответствие является отображением из
в
, причем имеют место равенства
Отображение в этом случае называют отображением, обратным к
.
Ограничение соответствия
Пусть — соответствие из
в
и
. Ограничением соответствия
на подмножества
и
(или
-ограничением соответствия
) называется соответствие из
в
, обозначаемое
, такое, что
Таким образом, -ограничение соответствия
есть «то же самое» соответствие
, но из последнего берутся только упорядоченные пары, первая компонента которых принадлежит подмножеству
, а вторая — подмножеству
. Можно записать
Так, «малый» арксинус, т.е. функция , есть ограничение «большого» арксинуса
, который является соответствием на подмножества
и
.
Рассмотрим некоторые важные частные случаи ограничений соответствий (в частности, бинарных отношений и отображений).
Всякое -ограничение соответствия
будем называть сужением соответствия
на подмножество
(коротко — C-сужением соответствия
), а всякое
-ограничение соответствия
— строгим сужением соответствия
на подмножество
(строгим C-сужением соответствия р). C-сужения соответствия
будем обозначать
, а строгое сужение —
соответственно.
Полезно заметить, что для любого отображения строгое сужение
есть сюръекция
на
. Если, сверх этого,
является инъекцией, то
есть биекция
на
. Допуская некоторую вольность речи, можно сказать, что любое отображение сюръективно отображает свою область определения на свою область значений, в частности, любая инъекция устанавливает взаимно однозначное соответствие между областью определения и областью значений. Так, функция
сюръективно отображает множество
всех действительных чисел на отрезок
, а любая показательная функция биективно отображает
на подмножество всех положительных действительных чисел.
Для бинарного отношения и любого подмножества
(M,M)-ограничение бинарного отношения называют ограничением бинарного отношения
на подмножество
и обозначают
. Можно записать
.
Рассмотрим, например, отношение естественного порядка на множестве действительных чисел. Тогда отношение
есть ограничение этого порядка на подмножество целых чисел. Но ни в коем случае нельзя путать это отношение с
-сужением отношения
! Это последнее состоит из всех таких упорядоченных пар
, что
и
, т.е. вторая компонента пары может быть произвольным действительным числом, не меньшим заданного целого
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение 2.5.
Композицией
бинарных отношений
и
,
заданных на множестве,
называют отношениетакое, что
|
|
(2.4) |
Примечание. В
формуле (2.4) использованы символы ««,
««,
««,
««.
Все эти символы взяты из математической
логики, которая рассматривается в главе
4. Однако многим эти символы известны
из школьного курса математики. Символназывают квантором всеобщности, он
заменяет слова «любой», «всякий»,
«каждый». Символ– квантор существования, его читают
как «существует», «найдется».
Символзаменяет слова «…тогда и только
тогда…», «…если и только если…»,
символзаменяет соединительные союзы «и»,
«а», «но» и пр. Так предложение
с этими символами в формуле (2.4) можно
прочитать следующим образом: «Для
любого элементаиз множества
и любого элемента
из этого же множества справедливо
утверждение: паратогда и только тогда, когда во множестве
найдется такой элемент
,
чтои
«.
Если во множестве
имеется элемент
,
через который осуществляется связь
между элементамии
в композиции отношений
,
то элементбудем называтьэлементом
посредником,
а саму связь между
и
–опосредованной
связью.
Пусть
={a,b,c}.
Отношения
и
заданы матрицами:
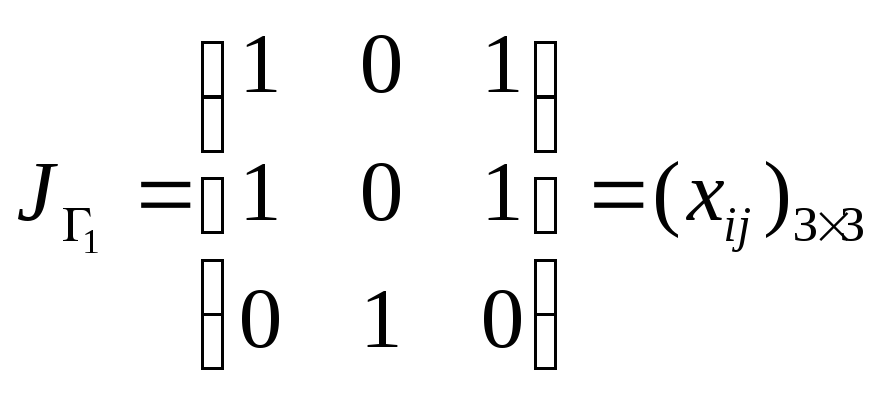

Найдем композицию
.
Для этого выполним следующую
последовательность действий:
1) используя матрицы
и
,
запишем графики отношений
и
:
,
;
2
построим графы отношений
и
и объединим их (рис. 2.2);
Примечание1. Графы
и
построены в виде двудольных графов,
причем входы графа
являются выходами графа
.
Примечание 2. Пути
в объединении графов
и
ведут от элементов множества
к их образам в отношении
,
и далее к образам в отношении
.
3) выпишем все пути,
ведущие от элементов a,
b
и c
к их образам в отношении
,
а также промежуточные элементы в этих
путях, посредством которых осуществляются
связи в отношении.
Результат представим в виде таблицы:
|
Пути |
Элементы, |
Элементы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) запишем график
отношения
и построим его граф (рис. 2.3).
Рассмотрим вопрос
об отыскании элементов композиции
отношений
и
,
не прибегая к графам.
Пусть



,
и
.
Задача состоит в том, чтобы найти способ
вычисления элементовматрицы
.
1. Найдем
.
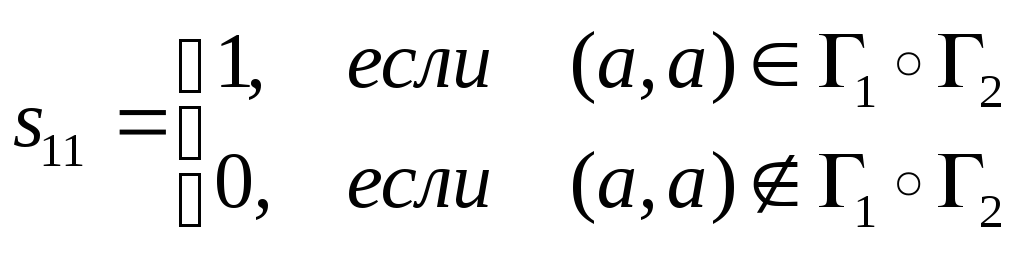
(см. определение 2.4). В свою очередь по
формуле (2.4), пара
тогда и только тогда, когда во множестве
найдется такой элемент
,
чтои
.
Рассмотрим эти включения для всех
возможных значений.
1)
;
,
так как=1;
,
так как=0.
Следовательно,
не является
элементом множества
,
который осуществляет опосредованную
связь междуи
в композиции отношений
.
Вывод о том, чтоне является
элементом посредником в паре
,
символически можно записать так:.
2)
;
,
так как=0;
,
так как=0.
Следовательно,
не является
элементом посредником в паре
и
.
3)
;
,
так как=1;
,
так как=1.
Следовательно,
осуществляет
опосредованную связь в паре
и
.
Таким образом, во
множестве
найден элемент
,
осуществляющий опосредованную связь
между элементами парыв композиции отношений
.
Следовательно,.
Последнее равенство
можно рассматривать как результат
умножения первой строки матрицы
на первый столбец матрицы
,
в которых умножение элементов матрицы
выполняется по правилу логического
умножения, а сложение произведений –
по правилу операции максимум (см. формулы
(1.8), (1.10)).
2. Найдем
,
воспользовавшись выводом, сделанным в
п. 1.

=.
Равенство
означает, что во множестве
есть элемент посредник
,
осуществляющий связь между элементами
парыв композиции отношений
.
Покажем, что это действительно так.
1)
является элементом посредником, поскольку
и
;
2)
не является элементом посредником, так
каки
;
3)
также не является элементом посредником,
поскольку,
но.
Аналогично находим
все элементы матрицы


элемент посредник
–
;

элемент посредник
–
;

элемент посредник
–
;

элемент посредник
–
;
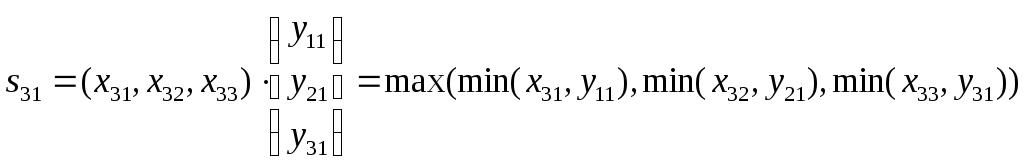
опосредованных
связей между
и
нет,
;

опосредованных
связей между
и
нет,
;

элемент посредник
–
.
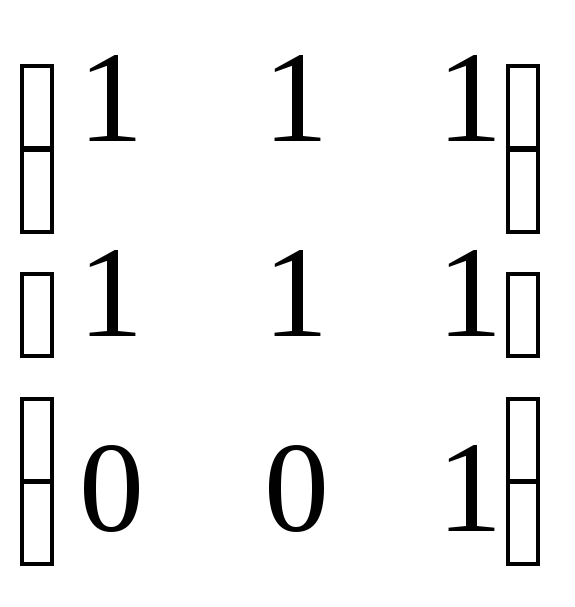
Таким образом,
матрица
имеет вид
Обобщением
проделанных операций являются формулы
(2.5) и (2.6), которые позволяют вычислять
матрицы композиций бинарных отношений
на произвольном множестве
:
|
|
(2.5) |
где
– число элементов множества
,
– матрица отношения
,
– матрица отношения
,
– матрица отношения
,
элементыкоторой находят по формуле (2.6):
|
|
(2.6) |
Рассмотрим
композицию
,
когда=
=
.
В этом случае естественно обозначить=
.
Учитывая формулу (2.5), получаем:.
Примеры.
1. Пусть
и
на множестве.
Найдем матрицу композиции
.

Для любой строки
матрицы
и соответствующей строки
матрицы
выполняются неравенства
(см. определение (1.5) и формулу (1.3)). Все
строки матрицыне меньше отношенующих строк матрицы
.
Будем считать, что в таком случае.
Очевидно, что из неравенстваследует
.
В матрице
учтены все связи между элементами
множества,
определяемые отношением,
в матрице– все дополнительные опосредованные
связи между элементами того же множества.
Неравенствоозначает, чтокаждая опосредованная
связь покрывается непосредственной
связью, т.е. в отношенииучтены все опосредованные связи.
2.
,


,
,
,
– строки матриц
и
.
Имеем неравенства:,
.
Строкии
несравнимы между собой.
В матрице
записаны все непосредственные связи,
определяемые отношением,
в матрице– дополнительные опосредованные связи
в этом же отношении.
Проанализируем неравенства
и
строк, соответствующих элементам
.
1)
означает, что опосредованная связь
(
–
элемент посредник) не покрывается
непосредственной связью меду этими
элементами в отношении:
,
но.
2)
говорит о том, что связь
только непосредственная, элемент
посредник, осуществляющий эту связь в
композиции отношений, отсутствует:,
но.
3)
,
означает, что связьявляется только опосредованной (
– элемент посредник):
,
но.
Таким образом, если строки
и
матриц
и
несравнимы или
,
то опосредованные связи между элементами
множества покрываются непосредственными
связями лишь частично или не покрываются
совсем.
Из рассмотренных
примеров делаем вывод.
Вывод. Если
в отношении
непосредственные связи между элементами
множествапокрывают все опосредованные связи
между его элементами, тои
.
Соседние файлы в папке учебник
- #
- #
- #
- #
- #
- #
- #
Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические и информационные объекты, процессы их функционирования. К числу последних я отношу, например, базы данных (реляционные базы данных (РеБД)). Не менее важной считаю область принятия решений, которая состоит из двух основных статистической и алгебраической, основанной целиком на теории отношений. Образовательный уровень специалистов в этой теории близок к нулю.
Откройте учебник по специализации и там увидите в лучшем случае об эквивалентностях, которые авторами трактуются весьма своеобразно. Одного защитившегося уже ДТН спрашиваю: Вы рассматриваете отношение эквивалентности на указывая ни носителя отношения, ни конкретного отношения, как оно у Вас выглядит в записи? Ответ: как выглядит — обыкновенно. Выясняется, что он обо всем этом имеет весьма смутное представление.
Публикаций по проектированию РеБД, кроме иностранных статей назвать затрудняюсь. В 90-х годах был оппонентом, писал отзыв на диссертацию, где рассматривались и иерархические, и сетевые, и реляционные БД. Но как-то год, полтора назад опять на отзыв пришла работа, автор пишет уже только о РеБД, о нормализации отношений БД, но теоретической новизны не показал. Во многих ВУЗах читается курс о базах данных, но не о том, как их создать, создать СУБД, а как правило, о том как эксплуатировать готовую (зарубежную) БД.
Преп. состав не готов научить специалистов IТ-шников создавать отечественные СУБД, ОS, языки программирования, я уж не говорю о БИС, СБИС, заказных БИС. Здесь, по-видимому, поезд ушел давно и надолго. Так что напрасно надуваются у некоторых щеки от гордости (читай снобизма) это видно по комментариям к чужим публикациям, покажите сами, что можете, а не балуйтесь никчемными переводами и перепевками чужого ради предмета гордости — «рейтинга» и «кармы». Сказывается не только отсутствие креатива, но простой образованности и воспитания.
Вторая предметная область неразрывно, связанная с отношениями, — принятие решений. Каждый из нас постоянно занят этим. Мы без решения осознанного или неосознанного пальцем не пошевелим. Мало кто понимает, а еще меньше пишет о решениях. В основе решения любого ЛПР (лица, принимающего решение) лежит предпочтение альтернатив. А моделью предпочтения как раз и является такой тип отношений, который назван «пространством отношений предпочтения». Но кто их изучает. Когда я пришел к «специалисту» по отношениям с вопросом о количестве отношений каждого типа, он не зная ответа, «убил» встречным вопросом, а зачем это Вам?
Понятие отношения
Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров, по-видимому, не приводили.
В моей памяти есть несколько на всю жизнь запомнившихся примеров. Об отображениях и об отношениях. Расскажу вначале об отображениях. Имеется два ведерка с краской. В одном белая в другом — черная. И есть коробка с кубиками (очень много). Грани имеют рельефные номера. Сколькими способами можно раскрасить грани кубиков в два цвета? Ответ неожиданный — столькими, сколько 6-разрядных двоичных чисел, или 26 = 64. Поясню подробнее ф: 2→6 отображаются 2 объекта в 6. Каждая строчка таблицы- дискретное отображение фi.
Построим таблицу с 6 колонками и краскам сопоставим число белая — нуль, черная — единица, а граням кубика колонки. Начинаем с того, что все 6 граней белые — это 6-мерный нулевой вектор. Вторая строчка одна грань черная, т. е. младший разряд заполнен 1. и так до исчерпания 6-разрядных двоичных чисел. Кубики ставим в общий длинный ряд. У каждого из них как бы появился номер от 0 до 63.
Теперь отображение наоборот. Пачка листов бумаги (много) и 6 красок (фломастеры).
Фломастерами разного цвета надо пометить обе стороны бумажных листов. Сколько листов потребуется. Ответ f: 6 → 2 или 62 =36. Речь идет о произвольных отображениях.
Перейдем к отношениям. Начнем с абстрактного множества — носителя отношения
А ={a1, a2, a3, …, an}.
О нем почитать можно здесь. Для лучшего понимания сократим множество до 3 элементов, т.е. А ={a1, a2, a3}. Теперь выполним декартово умножение А×А =А2,
А×А={(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)}.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Вначале простенький пример.
Пример 1. Задано множество А ={a,b,c,d} из 4-х элементов. Выписать все его подмножества. В(А) ={Ø};{a};{b};{c};{d};{ab};{ac};{ad};{bc};{bd};{cd};{abc};{abd};{acd};{bcd};{abcd}; 24 = 16 подмножеств. Это булеан В(А) множества А и в него включено пустое подмножество.
Подмножества будут содержать из А×А разное количество элементов (пар): одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество (Ø). Сколько же получилось подмножеств? Много, а именно 29= 512 элементов.
Определение. Любое подмножество декартова произведения (у нас квадрата) множества называется отношением. Заметим, в произведении используется одно и то же множество. Если множества разные, возникает не отношение, а соответствие.
Если декартово произведение из двух сомножителей, то отношение бинарное, если из 3-х -тернарное, из 4-х — тетрарное, из n — n-арное. Арность — число мест в отношении. Отношениям дают имена прописных букв R,H, P, S… Остановимся подробно на бинарных отношениях (БО), так как они играют очень важную роль в теории отношений. Собственно к бинарным отношениям могут быть сведены все остальные.
Символ отношения ставится слева от элементов R(x, y) или между ними x R y; х, у є А.
Определение Множество всех подмножеств множества А называется булеаном. Наш булеан состоит из 2|А×А| элементов, здесь|А×А| — мощность множества.
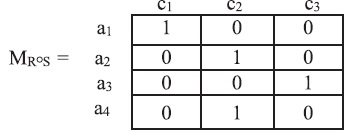
Отношения можно задавать в разном представлении над А={a1,a2,a3,a4}:
- перечислением элементов; R1={(a1,a2),(a1,a3),(a2,a3)(a2,a4)(a3,a2)(a3,a4}
- двоичным n = 16-разрядным вектором; <0110001101010000>;
- матрицей;
Рисунок 1.2. а)Матрица 4×4 бинарного отношения б) нумерация клеток Матрицы
Здесь используются номера клеток, заполненные единицами на рис. 1б)
— Векторное представление. Двоичный вектор для представления бинарного отношения формируется из элементов {0,1} следующим образом:
Рассмотренный пример задания отношения в векторной форме будет иметь следующий вид:
— Представление графом. Поставим в соответствие элементам множества
А ={x1,x2,z3,…,xn} точки на плоскости, т.е. вершины графа G = [Q, R].
Проведем в графе дугу от (xi) к (xj) тогда и только тогда, когда пара (xi,xj) є R (при i = j дуга (xi,xi) превращается в петлю при вершине (xi). Пример (рис. 1а) представления бинарного отношения A[4×4] графом изображен на рис.2.2.
Рисунок 2.2. Представление отношения ориентированным графом
Каталог бинарных отношений (n = 3)
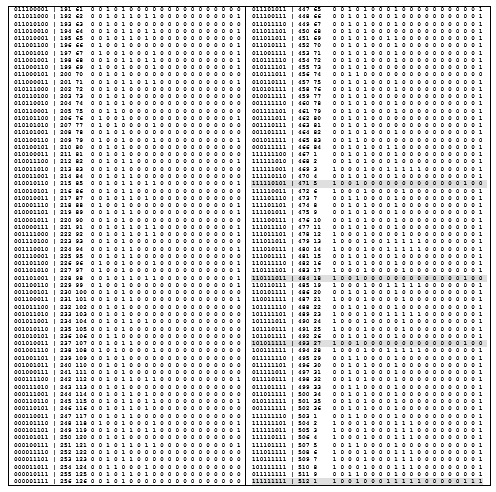
Большое видится на расстоянии. Чтобы почувствовать отношения их разнообразие, мощность мне пришлось вручную создать каталог бинарных отношений над множеством из 3-х элементов, который включил все (боле 500 отношений) отношения. После этого «дошло» или «зашло»об отношениях.
Очевидно, что в каталог войдут 23×3 = 29 отношений, и каждое из них снабдим набором присущих им свойств. Ниже (табл. 3) приводится полный список всех 512 отношений над множеством А, |A| = 3, из трех элементов. Приводятся также результаты подсчета количества отношений (табл. 2), представленных сочетаниями номеров клеток декартова квадрата 3×3, различных подклассов для различных значений мощности множества-носителя (n = 3). Для каждого отношения указаны его основные свойства и принадлежность типу (табл. 3). Сокращения, используемые в каталоге раскрываются таблицей 2
Таблица 2. Количественные характеристики каталога при разных n
Сущность производимых операций с отношениями и их технику удобно пояснять на примерах, которые особенно просты и понятны для бинарных отношений. В операциях могут участвовать, два и/или более отношений. Операции, выполняемые над отдельными отношениями – унарные операции. Например, операции обращения (получение обратного) отношения, взятие дополнения, сужение (ограничение) отношения. Как пользоваться каталогом поясним примером примером.
Пример 2. Рассмотрим строку Nпр =14 таблицы каталога. Она имеет вид
Первые 9 символов строки (справа от равенства) — это двоичный вектор, соответствующий сочетанию из 9 по 2, а именно, номер первой клетки (отсчет слева направо) номер 5-й клетки матрицы бинарного отношения, т.е. элементы а1а1= а2а2 =1. Это сочетание имеет порядковый номер Ncч = 4 и сквозной номер Nпр = 14 в списке всех отношений. В остальных позициях этой строки стоят либо нули, либо единицы. Нули свидетельствуют об отсутствии свойства, соответствующего названию колонки нуля, а единицы – наличие такого свойства у рассматриваемого отношения.
Свойства и количественные характеристики отношений
Рассмотрим наиболее важные свойства отношений, которые позволят в дальнейшем выделить типы (классы) отношений, применяющиеся в реляционных базах данных в теории выбора и принятия решений и других приложениях. Далее будем обозначать отношение символом [R,Ω]. R- имя отношения, Ω — множество-носитель отношения.
1. Рефлексивность. Отношение [R,Ω] называется рефлексивным, если каждый элемент множества находится в отношении R сам с собой (рис. 2.3). Граф рефлексивного БО имеет во всех вершинах петли (дуги), а матрица отношения содержит (Е) единичную главную диагональ.
Рисунок 2.3. Рефлексивное отношение
2. Антирефлексивность. Отношение [R,Ω] называется антирефлексивным, если ни один элемент из множества не находится в отношении R сам с собой (рис. 2.4). Антирефлексивные отношения называют строгими.
Рисунок 2.4. Антирефлексивное отношение
3. Частичная рефлексивность. Отношение [R,Ω] называется частично
рефлексивным, если один или более элементов из множества не находится в отношении R сам с собой (рис. 2.5).
4. Симметричность. Отношение [R,Ω] называется симметричным, если вместе с упорядоченной парой (х, у) отношение содержит и упорядоченную пару (у, х) (рис. 2.6).
5. Антисимметричность. Отношение [R,Ω] называется антисимметричным, если, если для всякой упорядоченной пары (х, у) є R упорядоченная пара
(у, х)єR, только в случае х = у. Для таких отношений R∩R-1 ⊆ E (рис. 2.7).
6. Асимметричность. Отношение [R,Ω] называется асимметричным, если оно антирефлексивно и для всякой упорядоченной пары (х, у) є R упорядоченная пара (у, х) ∉ R, для отношений R ∩ R-1 = Ø (рис. 2.8).
7. Транзитивность. Отношение [R,Ω] называется транзитивным, если для всяких упорядоченных пар (х, у),(у, z) є R, в отношении R найдется упорядоченная пара (х, z) є R или если R×R⊆R (рис. 2.9).
8. Цикличность. Отношение [R,Ω] называется циклическим, если для его элементов {x1, x2, z3,…, xn} найдется подмножество элементов {xi,xi+1,…xr,…,xj,xi}, для которого можно выписать последовательность xiRxi+1R…RxjRxi. Такая последовательность называется циклом или контуром (рис. 2.10).
9. Ацикличность. Отношения, в которых отсутствуют контуры называются, ациклическими. Для ациклических отношений выполняется соотношение Rk∩R = Ø для любого k > 1 (рис. 2.11).
10. Полнота (связность). Отношение [R,Ω] называется полным (связным), если для любых двух элементов (у, z) є Ω один из них находится в отношении с другим (рис 2.12). Линейность. Линейные отношения – это минимально полные отношения.
Рисунок 2.12. Линейное отношение
Итак, нами установлено, что отношения, как математические объекты, обладают определенными свойствами, определение которых приведены ранее. В следующем пункте рассмотрим существо и проявление некоторых свойств:
- Рефлексивность х є А (хRx).
- Антирефлексивность х є А ¬(хRx).
- Симметричность х, у є А (хRy→yRx).
- Антисимметричность (xRy & yRx→x = y).
- Транзитивность; х, у, z є А(хRy & yRz →xRz).
- Цикличность; х, у є А; .
- Полнота x,y є А (xRy, yRx);
- Связность (x ≠ y→ xRy, yRx).
- Линейность x,y є А (xRy, yRx).
Анализ пространства отношений представляет сложную задачу теории и, надо отметить, далек от завершения. К основным результатам следует отнести выделение подмножеств отношений, образующих полные пространства отношений со всеми вытекающими из этого следствиями.
Количественные соотношения таких дискретных пространств представляют большой как
теоретический, так и практический интерес. Ниже рассматриваются некоторые аспекты количественных характеристик, связанных со свойствами отношений разных типов.
Операции над отношениями
Как и большинстве систем счисления с отношениями выполняются операции:
- унарные;
- бинарные;
- n-арные.
Ниже приведены таблицы булева ⊕ сложения и умножения & двух переменных x1 и x2, сложение по mod 2 и суммирование двоичных чисел:
Выше было введено понятие бинарного отношения, как подмножества упорядоченных пар декартова произведения множеств, а также были рассмотрены свойства отношений. Кроме того, были упомянуты бинарные отношения и матричное представление отношений. Рассмотрим теперь понятие отношения более подробно, кроме того, рассмотрим основные операции бинарных отношений, наиболее важные из всего их множества для отношений.
Для них должны выполняться следующие условия:
- арность операндов в операции должна совпадать;
- результатом операции должно быть отношение той же арности.
Для бинарных и n-арных отношений должно быть выполнено: область прибытия первого операнда должна совпадать с областью отправления второго операнда.
Унарные операции над отношениями
Обращение отношений. Обратным к отношению R называется отношение R-1, определяемое условием xR-1y<=>yRx. Более корректно эту операцию следовало бы назвать псевдообращением, так как р·р-1 ≠ Е = Δ.
Пусть отношение Р записано в форме перечисления входящих в него упорядоченных пар. Если в каждой паре поменять местами компоненты, то новые пары образуют отношение P-1, которое называют обратным к Р.
Обратное отношение к отношению P – такое отношение, которое образовано парами (ai aj), для которых (aj ai) є P-1. Для отношений в матричной форме обратные отношения получаются путем транспонирования матрицы Р.
9. Двойственное отношение (Pd) к отношению Р – отношение, образованное всеми теми парами, которые принадлежат универсальному отношению и не принадлежат обратному отношению (дополнение к обратному):
Pd = {(ai aj) | ((ai aj) єA×A) & (ai aj)∉
P
-1)} =(A×A) P-1.
Двойственное и обратное отношения в совокупности содержат все пары декартова произведения A×A и не имеют общих пар, они также как и отношения Р и
P
образуют разбиение A×A
Заметим, что ни для какого отношения Р не выполняется Р= Pd.
Сужение (РА1). Отношение [R1, A1] называется сужением отношения [R, A] на множество Ω1, если Ω1⊆ Ω и R1=R∩Ω1×Ω1. Отношение РА1 на множестве А1 ⊆ А – отношение РА1 на множестве А1, образованное всеми теми парами, которые принадлежат отношению Р и одновременно входят в состав декартова произведения А1 × А1. Другими словами, РА1 – пересечение отношений Р и А1×А1. Пусть А1 = {a1, a3, a4}, тогда для отношений Р и Q в матричной форме отношения сужения будут иметь вид:
Бинарные операции
Операции, требующие не менее двух отношений – n-арные (n-местные). В таких операциях могут участвовать отношения только одинаковой арности. Примеры таких операций: пересечение, объединение, разность, симметрическая разность отношений и некоторые другие. Если в операции используется более чем два отношения, то она выполняется последовательно для двух первых, а затем для итогового отношения и третьего и т.д.
Иначе говоря, эти операции определены для двух отношений. При операциях над отношениями предполагается, что области задания отношений (операндов и результата) совпадают, арности отношений совпадают, и результатом операции снова является отношение той же арности. В качестве примеров будем рассматривать операции над бинарными отношениями P и Q, заданными на дискретном множестве
А = {a1, a2, a3, a4} булевыми матрицами (нули в матрицу, как правило, не вписываются):
1. Пересечение (P ∩ Q) – отношение, образованное всеми теми парами элементов из А, которые входят в оба отношения, т.е. общие для P и Q,
P ∩ Q = {(ai aj) | ((ai aj) є P) & ((ai aj) є Q)}.
Матрица отношения P ∩ Q получается как булево пересечение матриц P и Q:
При отсутствии таких общих пар говорят, что пересечение отношений пусто, т.е. оно является нуль-отношением. Пересечением отношений R1 и R2 (R1∩R2 ) называется отношение, определяемое пересечением соответствующих подмножеств из А×А.
2. Объединение (PUQ). Объединением отношений R1 и R2 (R1UR2 ) называется отношение, определяемое объединением соответствующих подмножеств из А×А. Отношение, образованное всеми парами, составляющими или отношение P, или отношение Q, т.е. парами, принадлежащими хотя бы одному из отношений (связка ∨ — или объединительная)
P U Q = {(ai aj) | ((ai aj) є P) ∨ ( (ai aj) є Q)}.
Если в множестве А×А нет других пар, не вошедших в отношение PUQ, а пересечение их нулевое, то говорят, что отношения P и Q при объединении образуют полное отношение А×А, а их система – разбиение этого полного отношения. Объединение матриц отношений образуется как булева сумма матриц отношений:
3.Разность (PQ) – отношение, образованное теми парами из Р, которые не входят в отношение Q
PQ = {(ai aj) | ((ai aj) є P)&((ai aj)∉Q)}.
Разность для отношений в матричном представлении имеет вид
4. Умножение отношений. Упорядоченные пары, образующие отношения могут содержать одинаковые элементы, а могут и не содержать. Среди пар, имеющих в своем составе одинаковые элементы, выделим такие упорядоченные пары, которые назовем смежными (примыкающими) и которые имеют во второй паре 1-й элемент, а в первой паре 2-й элемент один и тот же. Определим произведение смежных пар как упорядоченную пару:
( ai ak)∙( ak aj) => (ai aj).
В терминах теории графов сказанное означает, что смежные пары образуют маршрут из точки (ai) в точку (aj) транзитом через точку (ak), состоящий из 2-х смежных дуг. Произведение этих дуг – третья дуга из точки (ai) в точку (aj), реализующая переход между крайними точками маршрута в том же направлении, минуя промежуточную точку (ak). Говорят, что дуга (ai aj) замыкает эти точки напрямую.
5. Симметрическая разность (P∆Q) – отношение, образованное теми парами, которые входят в объединение PUQ, но не входят в пересечение P∩Q. Другая форма определения объясняет название операции: P∆Q образовано теми упорядоченными парами, которые являются объединением разностей PQ и QP. Таким образом, выражение для симметрической разности записывается двумя разными способами:
P∆ Q = (PU Q)(P ∩ Q) = (PQ)U (QP).
Матрица симметрической разности имеет вид:
Из последней записи следует, что операция симметрической разности допускает перестановку операндов, т. е. коммутативна.
5. Композиция или произведение (P∙Q) – отношение, образованное всеми парами, для которых выполняется:
P∙Q = {(ai aj)|((ai ak) є P) & ((ak aj) є Q)}.
Другими словами, каждая упорядоченная пара в результирующем отношении есть результат умножения смежных пар, из которых 1-я пара принадлежит первому сомножителю-отношению, 2-я – второму сомножителю-отношению. Операция композиции не коммутативна.
Композиция (Р◦Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда существует Z є M такое, что (x, z) є P и (z, y) є Q.
При матричном представлении отношений матрица композиции отношений равна булеву произведению матриц исходных отношений:
Частный случай композиции отношений – квадрат отношения.
Можно показать, используя индукцию, что n-я степень отношения определяется рекуррентно по формуле:Pn=Pn-1◦Р, это означает, что пара (x,y) є Pn в том случае, когда в матрице Р существует цепочка элементов: такая, что (xi, xi+1)є P, 1<i<n–1.
Операция композиции обладает свойством ассоциативности (как произведение матриц).
Композиция отношений на множестве М – результат попарной композиции отношений при любой расстановке скобок. Область задания результата композиции при этом не меняется.
Композиция для булевых матриц отношений образуется в результате булева произведения матриц этих отношений.
Таблица 3. Каталог бинарных отношений (n = 3). Кликабельно
Литература
1. Авдошин С.М., Набебин А.А. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. -352 с.
2. Акимов О.Е. Дискретная математика.Логика, группы, графы- М.: Лаб.Баз. Зн., 2001. -352 с.
3. Андерсон Д.А. Дискретная математика и комбинаторика.- М.: Вильямс, 2003. -960 с.
4. Берлекэмп Э. Алгебраическая теория кодирования. -М.: Мир,1971.- 478 с.
5. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 1- СПб.: ВКА им. А.Ф. Можайского, 2015. -219 с.
6. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 2- СПб.: ВКА им. А.Ф. Можайского, 2017. -151 с.
7. Горенстейн Д. Конечные простые группы.Введение в их классификацию.-М.: Мир,1985.- 352 с.
8. Грэхем Р., Кнут Д., Пташник О. Конкретная математика.Основание информатики.-М.: Мир,1998.-703 с.
9. Дейт К. Введение в системы баз данных. -М.: Наука,1980. -463 с.
10. Елизаров В.П. Конечные кольца.- М.: Гелиос АРВ,2006. — 304 с.
Иванов Б.Н. Дискретная математика: алгоритмы и программы-М.: Лаб.Баз. Знаний., 2001. -280 с.
11. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения-М.: Вузовская книга, 2000.-280 с.
12. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.-М.: Наука, 1973.-832 с.
13. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.1 -М.: Мир,1988. — 430 с.
14. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.2 -М.: Мир,1988. — 392 с.
15. Ляпин Е.С., АйзенштатА.Я., Лесохин М.М., Упражнения по теории групп.-М.: Наука,1967.-264 с.
16. Мейер Д. Теория реляционных баз данных. -М.: Мир, 1987.- 608 с.
17. Муттер В.М. Основы помехоустойчивой телепередачи информации. -Л. Энергоатомиздат,1990.- 288 с.
18. Нагао М., Катаяма Т., Уэмура С. Структуры и базы данных. — М.: Мир, 1986. — 197 с.
19. Наумов А.Н. и др. Системы управления базами данных и знаний.-М.: Финансы и статистика,1991.-352 с.
20. Набебин А.А.Дискретная математика.- М.: Лаб.Баз. Знаний., 2001. -280 с.
21. Новиков Ф.А. Дискретная математика для программистов.- СПб.: Питер, 2000. -304 с.
22. Розенфельд Б.А. Многомерные пространства.-М.: Наука,1966.-648 с.
23. Ульман Дж. Основы систем баз данных. — М.: Финансы и статистика,1983.-334 с.
24. Холл М. Теория групп.-М.: Изд. ИЛ, 1962.- 468 с.
25. Шиханович Ю.А. Группы, кольца, решётки. — СПб.: Кирцидели,2006. — 368 с.
26. Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях: В 2-х ч Ч.2.-Мн.: Выш. шк., 1987. -256 с.
27. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел.- Минск: Дизайн ПРО,2000. -240 с.
From Wikipedia, the free encyclopedia
In the mathematics of binary relations, the composition of relations is the forming of a new binary relation R; S from two given binary relations R and S. In the calculus of relations, the composition of relations is called relative multiplication,[1] and its result is called a relative product.[2]: 40 Function composition is the special case of composition of relations where all relations involved are functions.
The word uncle indicates a compound relation: for a person to be an uncle, he must be the brother of a parent. In algebraic logic it is said that the relation of Uncle (


Beginning with Augustus De Morgan,[3] the traditional form of reasoning by syllogism has been subsumed by relational logical expressions and their composition.[4]
Definition[edit]
If 

their composition 
In other words, 





Notational variations[edit]
The semicolon as an infix notation for composition of relations dates back to Ernst Schroder’s textbook of 1895.[6] Gunther Schmidt has renewed the use of the semicolon, particularly in Relational Mathematics (2011).[2]: 40 [7] The use of semicolon coincides with the notation for function composition used (mostly by computer scientists) in category theory,[8] as well as the notation for dynamic conjunction within linguistic dynamic semantics.[9]
A small circle 


Further with the circle notation, subscripts may be used. Some authors[11] prefer to write 


The binary relations 

Properties[edit]
Composition in terms of matrices[edit]
Finite binary relations are represented by logical matrices. The entries of these matrices are either zero or one, depending on whether the relation represented is false or true for the row and column corresponding to compared objects. Working with such matrices involves the Boolean arithmetic with 

Heterogeneous relations[edit]
Consider a heterogeneous relation 








If for all 








In this case 
The composition 

Example[edit]
Let 




Since both 


The converse relation 




This matrix is symmetric, and represents a homogeneous relation on
Correspondingly, 

Vice versa, the question whether two given nations share a language can be answered using 
Schröder rules[edit]
For a given set 


In the calculus of relations[15] it is common to represent the complement of a set by an overbar: 
If 

Verbally, one equivalence can be obtained from another: select the first or second factor and transpose it; then complement the other two relations and permute them.[5]: 15–19
Though this transformation of an inclusion of a composition of relations was detailed by Ernst Schröder, in fact Augustus De Morgan first articulated the transformation as Theorem K in 1860.[4] He wrote[16]
With Schröder rules and complementation one can solve for an unknown relation 
For instance, by Schröder rule 



Quotients[edit]
Just as composition of relations is a type of multiplication resulting in a product, so some operations compare to division and produce quotients. Three quotients are exhibited here: left residual, right residual, and symmetric quotient. The left residual of two relations is defined presuming that they have the same domain (source), and the right residual presumes the same codomain (range, target). The symmetric quotient presumes two relations share a domain and a codomain.
Definitions:
Using Schröder’s rules, 





One can practice the logic of residuals with Sudoku.[further explanation needed]
Join: another form of composition[edit]
A fork operator 









Another form of composition of relations, which applies to general 

See also[edit]
- Demonic composition
- Friend of a friend – Human contact that exists because of a mutual friend
Notes[edit]
- ^ Bjarni Jónssen (1984) «Maximal Algebras of Binary Relations», in Contributions to Group Theory, K.I. Appel editor American Mathematical Society ISBN 978-0-8218-5035-0
- ^ a b c Gunther Schmidt (2011) Relational Mathematics, Encyclopedia of Mathematics and its Applications, vol. 132, Cambridge University Press ISBN 978-0-521-76268-7
- ^ A. De Morgan (1860) «On the Syllogism: IV and on the Logic of Relations»
- ^ a b Daniel D. Merrill (1990) Augustus De Morgan and the Logic of Relations, page 121, Kluwer Academic ISBN 9789400920477
- ^ a b c Gunther Schmidt & Thomas Ströhlein (1993) Relations and Graphs, Springer books
- ^ Ernst Schroder (1895) Algebra und Logik der Relative
- ^ Paul Taylor (1999). Practical Foundations of Mathematics. Cambridge University Press. p. 24. ISBN 978-0-521-63107-5. A free HTML version of the book is available at http://www.cs.man.ac.uk/~pt/Practical_Foundations/
- ^ Michael Barr & Charles Wells (1998) Category Theory for Computer Scientists Archived 2016-03-04 at the Wayback Machine, page 6, from McGill University
- ^ Rick Nouwen and others (2016) Dynamic Semantics §2.2, from Stanford Encyclopedia of Philosophy
- ^ John M. Howie (1995) Fundamentals of Semigroup Theory, page 16, LMS Monograph #12, Clarendon Press ISBN 0-19-851194-9
- ^ Kilp, Knauer & Mikhalev, p. 7
- ^ ISO/IEC 13568:2002(E), p. 23
- ^ Unicode character: Z Notation relational composition from FileFormat.info
- ^ Irving Copilowish (December 1948) «Matrix development of the calculus of relations», Journal of Symbolic Logic 13(4): 193–203 Jstor link, quote from page 203
- ^ Vaughn Pratt The Origins of the Calculus of Relations, from Stanford University
- ^ De Morgan indicated contraries by lower case, conversion as M−1, and inclusion with )), so his notation was
- ^ Gunther Schmidt and Michael Winter (2018): Relational Topology, page 26, Lecture Notes in Mathematics vol. 2208, Springer books, ISBN 978-3-319-74451-3
References[edit]
- M. Kilp, U. Knauer, A.V. Mikhalev (2000) Monoids, Acts and Categories with Applications to Wreath Products and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter,ISBN 3-11-015248-7.
Текущая страница: 6 (всего у книги 16 страниц) [доступный отрывок для чтения: 3 страниц]
2.4. Представление отношений
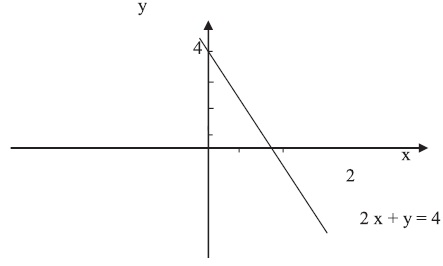
Как и множества, отношения можно изображать графически. Самый известный пример отношений дают уравнения. Рассмотрим отношение Р на множестве вещественных чисел R, т. е. Р является подмножеством множества R × R. Поскольку R2 представляет собой множество точек плоскости, то можно выразить Р через те точки плоскости, которые принадлежат Р. Обычно отношение Р состоит из всех пар вещественных чисел, которые обращают уравнение в ноль. Рассмотрим следующий пример.
Пример 2.5
Пусть имеется отношение Р, определяемое уравнением
2 x + y = 4.
Р содержит все пары (x, y), которые удовлетворяют уравнению. Графиком этого уравнения является прямая (рис. 2.2).
Рис. 2.2
Представление отношений для конечных множеств
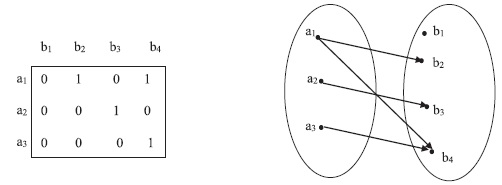
Пусть А и В два конечных множества. Отношение R между этими множествами можно представить:
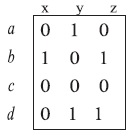
1) в виде прямоугольной матрицы из 0 и 1 – строки матрицы размечены элементами из А, а столбцы – элементами из В:
2) в виде двух непересекающихся дисков – один для множества А и другой для В. Если имеется отношение из А в В, то стрелка направлена от a к b, если (a, b) ∈ R.
Например, если A = {a1, a2, a3}, B = {b1, b2, b3, b4} и R = {(a1, b2), (a1, b4), (a2, b3), (a3, b4)}, то матрица отношений и стрелочная диаграмма для R показаны на рис. 2.3.
Рис. 2.3
Представление отношения в виде ориентированного графа
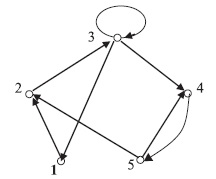
Имеется еще один способ представления отношений. Он используется, когда имеется отношение R для некоторого конечного множества А с самим собой. Пусть на множестве А = (1, 2, 3, 4, 5} имеется отношение
R = {(1, 2), (2, 3), (3, 1), (3, 3), (3, 4), (4, 5), (5, 2), (5, 4)}.
Поставим в соответствие каждому элементу множества А вершину графа, а каждой паре отношения – ориентированное ребро (дугу), при этом стрелка направлена от вершины, соответствующей первой паре, к вершине второй пары (рис. 2.4).
Рис. 2.4
2.5. Композиция отношений
Пусть имеются множества А, В и С, и пусть R отношение из А в В, а S отношение из В в С. Тогда R будет подмножеством А × В и S будет подмножеством В × С. Отношения R и S позволяют построить новое отношение из А в С, которое обозначается R ○ S и которое определяется как
а(R ○ S)с, если для некоторого b ∈ B выполняется аRb и bSc.
Другими словами,
R ○ S = {(a, c): когда существует b ∈ B, для которого (a, b) ∈ R и (b, c) ∈ S}.
Отношение R ○ S называется композициейR и S (или составным отношением). Иногда композиция обозначается просто RS.
Допустим, что R является отношением на множестве А, т. е. R является отношением из множества А в себя. Тогда R ○ R представляет композицию R с самим собой и иногда обозначается R2. Подобным же образом R3 = R2 ○ R = R ○ R ○ R и так далее для любого положительного n.
Из записи отношений R и S следует, что они применяются слева направо, сначала применяется R и затем S, однако иногда имеется в виду обратный порядок
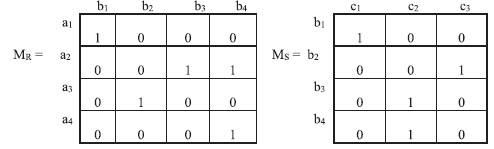
Пример 2.6. Пусть А = {a1, a2, a3, a4}, B = {b1, b2, b3, b4}, C = = {c1, c2, c3} и пусть
R = {(a1, b1), (a2, b3), (a2, b4), (a3, b2), (a4, b4)} и S = {(b1, c1), (b2, c3), (b3, c2), (b4, c2)}.
Рассмотрим стрелочную диаграмму.
На этой диаграмме имеется стрелка из a1 в b1 и затем из b1 в с1, т. е. имеется путь, который соединяет элемент a1 ∈ А с элементом с1 ∈ С. Другими словами,
a1(R ○ S)с1, поскольку a1Rb1 и b1Sс1.
Кроме этого, есть путь из a2 в с2, путь из a3 в с3 и путь из a4 в c2. Никаких других элементов из А, соединенных с С, нет и поэтому
R ○ S = {((a1, с1), (a2, с2), (a3,с3), (a4,c2)}.
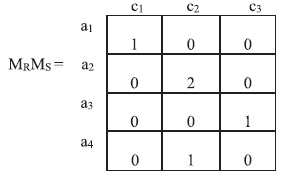
Композиция отношений и матрицы
Если имеются отношения R и S, тогда композицию R ○ S можно найти с помощью матриц. Обозначим через MR и MS матрицы отношений R и S соответственно.
Умножая матрицу MR на матрицу MS, мы получим матрицу M = MRMS, определяющую отношение R ○ S:
Все ненулевые элементы матрицы M определяют отношение R ○ S (можно просто заменить ненулевые элементы на 1 и получится матрица отношения R ○ S).
Композиция отношений ассоциативна (как ассоциативно и умножение матриц).
Теорема 2.1. Пусть A, B, C, D – некоторые множества, и пусть R отношение из А в В, S отношение из В в С и Т отношение из С в D. Тогда
(R ○ S) ○ T = R ○ (S ○ T).
Необходимо показать, что каждый элемент (каждая пара) отношения (R ○ S) ○ T принадлежит также и отношению R ○ (S ○ T). Возьмем пару (a, d) ∈ (R ○ S) ○ T. Тогда существует с в множестве С, что (a, c) ∈ R ○ S, и при этом (c, d) ∈ T, а так как (a, c) ∈ R ○ S, то существует и b в В, что (a, b) R и (b, c) ∈ S.
Поскольку (b, c) ∈ S и (c, d) ∈ T, то мы имеем (b, d)∈ S ○ T, а так как (a, b) ∈ R и (b, d) ∈ S ○ T, то тогда (a, d) ∈ R ○ (S ○ T). Поэтому (R ○ S) ○ T ⊆ R ○ (S ○ T). Аналогично можно показать и обратное включение R ○ (S ○ T) ⊆ (R ○ S) ○ T.
2.6. Свойства отношений
Отношение представляет собой подмножество произведения множеств. Изучение таких подмножеств оказывается очень продуктивным, если известны свойства, которыми могут обладать отношения. Пусть имеется множество А. Имеется пять важных свойств, которые определены на А.
Рефлексивность
Отношение R на множестве А является рефлексивным, если пара (a, a) ∈ R для каждого a ∈ A, или aRa для каждого a ∈ A. Отношение R не рефлексивно, если существует элемент a ∈ A, такой что (a, a) ∉ R.
Пример 2.7. Пусть на множестве А = {1, 2, 3, 4, 5} имеются следующие отношения:
R1 = { (1, 1), (2, 1), (2, 2), (3, 4), (4, 5)},
R2 = {1, 1), (1, 2), (2, 2)},
R3 = {(1, 1), (1, 2), (2, 2), (3, 3), (4, 4), (4, 5), (5, 5)},
R4 = Ø (пустое отношение),
R5 = A × A = U (универсальное отношение).
Определить, какие из этих отношений рефлексивны.
Рефлексивны только отношения R3 и R5, поскольку только они содержат все пять пар (1, 1), (2, 2), (3, 3), (4, 4), (5, 5). Пять, потому что в множестве А пять элементов.
Пример 2.8. Пусть имеются следующие отношения:
(а) отношение ≤ (меньше или равно) на множестве Z целых чисел,
(b) отношение = (равно) на множестве целых чисел,
(c) отношение
(перпендикулярно) на множестве прямых на плоскости,
(d) отношение делимости │ на множестве натуральных чисел N (a│b означает, что a делит b, т. е. существует такое натуральное x, что ax = b).
Определить, какие из этих отношений рефлексивны.
Отношение (c) не рефлексивно, поскольку прямая на плоскости неперпендикулярна сама себе. Остальные отношения рефлексивны.
Симметричность
Отношение R на множестве А является симметричным, если для каждой пары (a, b) ∈ R имеется пара (b, а) ∈ R, т. е. всякий раз, когда выполняется aRb, выполняется и bRа. Отношение R не симметрично, если существуют a∈А и b∈В, такие что (a, b) ∈ R, но (b, а) ∉ R.
Пример 2.9. Пусть А = {1, 2, 3} и отношения R представлены следующими орграфами (рис. 2.6 и 2.7). Симметричны ли эти отношения?
Рис. 2.6
Рис. 2.7
Отношение R1 на рис. 2.6 симметрично, а отношение R2 на рис. 2.7 не симметрично, поскольку для пары (1, 2) нет пары (2, 1).
Пример 2.10. Рассмотрим следующие отношения:
(a) отношение параллельности прямых на плоскости,
(b) отношение «учиться в одной группе» (для множества студентов университета),
(c) отношение «быть выше ростом» (для множества студентов университета),
(d) пусть А = {1, 2, 3, 4, 5} и отношение R означает, что если (a, b) ∈ R, то a + b является простым числом.
Определить, симметричны ли эти отношения.
(a) Отношение симметрично, поскольку если прямая a параллельна прямой b, то и прямая b будет параллельна прямой a.
(b) Отношение симметрично.
(c) Отношение не симметрично, если a выше ростом b, то b не выше чем а.
(d) Отношение симметрично, поскольку если a + b простое число, то и b + a простое число.
Антисимметричность
Отношение R на множестве А является антисимметричным, если для каждой пары (a, b) ∈ R имеется пара (b, а) ∈ R; только тогда, когда a = b, т. е. если aRb и bRа, то тогда a = b. Отношение R не антисимметрично, если существуют a ∈ А и b ∈ В, такие что (a, b) ∈ R и (b, а) ∈ R, но a ≠ b.
Пример 2.11. Пусть А = {1, 2, 3, 4} и отношения R1 и R2 представлены следующими орграфами (рис. 2.8 и 2.9). Антисимметричны ли эти отношения?
Рис. 2.8
Рис. 2.9
Отношение R1 на рис. 2.8 антисимметрично, а R2 на рис. 2.9 нет, потому что наряду с парой (1, 2) имеется пара (2, 1) и 1 ≠ 2.
Пример 2.12. Определить, какие из отношений антисимметричны:
(a) отношение ≤ (меньше или равно) на множестве целых чисел Z,
(b) отношение включения ⊆ на совокупности множеств,
(c) деление на множестве натуральных чисел N (m | n означает, что m является делителем n),
(d) пусть М – множество квадратных матриц порядка n с элементами из нулей и единиц. Пусть отношение R означает, что для матриц А, В ∈ M произведение А × В равно единичной матрице I, т. е. (А, В) ∈ R, если А × В = I.
(a) Отношение ≤ является антисимметричным, потому что если а ≤ b, то b ≤ a, только если a = b.
(b) Отношение включения ⊆ антисимметрично, потому что если А ⊆ В и В ⊆ А, то тогда А = В.
(c) Отношение деления на множестве натуральных чисел антисимметрично, поскольку m делит n (m | n) и n делит m (n | m) только тогда, когда m = n.
(d) Отношение R для матриц из М не является антисимметричным, потому что если А × В = I, то и В × А = I. Например:
Необходимо заметить, что отношения симметричности и антисимметричности не являются отрицанием одно другого. Если отношение не симметрично, то оно не обязательно должно быть антисимметричным, и наоборот. Например, пусть А = {1, 2, 3} и пусть отношение R1 = {(1, 1), (2, 2), (3, 3)}, а отношение R2 = {(1, 2), (2, 1), (2, 3)}. Тогда отношение R1 симметрично и антисимметрично, а отношение R2 не симметрично и не антисимметрично.
Транзитивность
Отношение R на множестве А транзитивно, если для каждых пар (a, b) ∈ R и (b, c) ∈ R, пара (a, c) ∈ R, т. е. если имеются aRb и dRc, то обязательно aRc. Отношение R не транзитивно, существуют такие элементы a, b, c ∈ A, что (a, b) ∈ R и (b, c) ∈ R, но пара (a, c) ∉ R.
Пример 2.13. Определить, какие из отношений транзитивны:
(a) пусть А = {1, 2, 3, 4} и R = {(1, 2),(1, 3), (2, 3), (4, 4)},
(b) пусть отношение R задано на множестве натуральных чисел N и означает (a, b) ∈ R, если a ≡ b (mod m) (числа a и b называются конгруэнтными по модулю m, если m является делителем (a—b), где m – целое число),
(с) отношения R1, R2, R3 на рис. 2.10.
Рис. 2.10
(a) Отношение R транзитивно.
(b) Отношение R транзитивно, потому что если a ≡ b (mod m) и b ≡ c (mod m), то тогда a ≡ с (mod m).
Например, пусть а = 3, b = 7, с = 11 и m = 4, тогда 3 ≡ 7(mod 4), 7 ≡ 11 (mod 4) и 3 ≡ 11 (mod 4), т. е. числа 3, 7 и 11 конгруэнтны по модулю 4, потому что все они имеют один и тот же остаток 3 при делении на 4.
(с) R1 и R2 – транзитивны, R3 не транзитивно.
2.7. Замыкание свойств
Пусть имеется множество А и семейство всех отношений на А, и пусть Р некоторое свойство этих отношений, например симметричность или транзитивность. Отношение со свойством Р называется Р-отношением. Отношение называется Р-замыканием некоторого отношения R на А (пишется P(R)), если оно является Р-отношением и R ⊆ P(R) ⊆ S, для каждого P-отношения S, содержащего R. Принято писать рефлексивное замыкание (R), симметричное замыкание (R), транзитивное замыкание (R), для рефлексивного, симметричного и транзитивного замыканий.
Отношение P(R) может, вообще говоря, и не существовать, однако в целях обобщения оно может быть всегда построено.
Обозначим
А = {(a, a): a ∈ A} диагональное отношение или отношение равенства на множестве А. Тогда замыкания отношений можно получать следующим образом.
Пусть R отношение на А, тогда:
1) R ∪
А является рефлексивным замыканием R;
2) R ∪ R-1 является симметричным замыканием R.
Пример 2.14. Рассмотрим следующее отношение R на А = {1, 2, 3, 4, 5 }.
R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 4), (3, 5), (5, 5) }.
Рефлексивное замыкание (R) = R ∪ {(2, 2), (3, 3), (4, 4)}.
Симметричное замыкание (R) = R ∪ {(3, 2), (4, 3), (5,3)}.
Нахождение транзитивного замыкания можно выполнить с помощью композиции отношений. Так, R2 = R ○ R, Rn = Rn-1 ○ R. Поскольку нахождение транзитивных замыканий отношения при большом числе элементов является весьма трудоемкой задачей(эквивалентной определению ориентированных путей в орграфе), то одним из способов ее решения оказывается возведение в степень матрицы отношений(матрицы смежности орграфа). Так, если R отношение на множестве А с n элементами, то транзитивное замыкание (R) = R ∪ R2 ∪ … Rn.
2.8. Отношение эквивалентности
Рассмотрим непустое множество S. Отношение R на S называется отношением эквивалентности, если R рефлексивно, симметрично и транзитивно.
1) для каждого a ∈ S, (a, a) ∈ R;
2) если (a, b) ∈ R, то (b, a) ∈ R;
3) если (a, b) ∈ R и (b, c) ∈ R, тогда (a, с) ∈ R.
Общая идея отношения эквивалентности состоит в том, что оно позволяет классифицировать объекты, которые в некотором смысле «похожи». Фактически, отношение равенства “—” на любом множестве S это отношение эквивалентности:
1) а = а для каждого a ∈ S.
2) если a = b, тогда b = a.
3) если a = b и b = c, тогда a = c.
Следует заметить, что отношение неравенства не является отношение эквивалентности. Например, 2 ≠ 3 и 3 ≠ 2, но 2 = 2.
Пример 2.15.
Пусть имеется множество треугольников на плоскости. Отношение конгруэнтности и подобия треугольников являются отношениями эквивалентности.
Классификация животных по видам. Отношение «в том же виде» есть отношение эквивалентности на множестве животных.
Отношение эквивалентности и разбиения
Разбиением Р множества S называется семейство {Ai} непустых подмножеств S со следующими свойствами:
1) каждый элемент а ∈ S, принадлежит к некоторому Аi;
2) если Аi ≠ Aj, тогда Ai ∩ Aj = Ø.
Иначе говоря, разбиение Р является разбиением S на непересекающиеся непустые подмножества.
Пусть R-отношение эквивалентности на множестве S. Для каждого а из S пусть [a] определяет множество элементов из S, с которыми а связано по отношению R, т. е.
[a] = {x: (a, x) ∈ R}
и называется классом эквивалентности а в S. Любой элемент из [a] называется представителем класса эквивалентности.
Семейство всех классов эквивалентности из S по отношению эквивалентности R обозначается как S / R и S / R = {[a]: a ∈ S}.
Пример 2.16.
(a) Пусть S = {1, 2, 3, 4, 5} и отношение
R = {(1, 1), (1, 2), (2, 1), (1, 3), (2, 2), (2, 3), (3, 2), (3,3), (3, 1), (4, 4), (4, 5), (5, 4), (5, 5)}.
Можно показать, что R рефлексивно, симметрично и транзитивно, т. е. является отношением эквивалентности. Найдем представителей каждого класса эквивалентности.
{1] = {1, 2, 3}, [2] = {1, 2, 3}, [3] = {1, 2, 3}, [4] = {4, 5}, [5]={4, 5}.
Классы [1] = [2] = [3] и [4] = [5] и S / R = {[1], [4] } являются разбиением S. В качестве представителей класса эквивалентности можно выбрать также либо {[1], [5]}, либо {2], [4]}, {[2], [5]} и т. д.
(b) Пусть R4 является отношением на множестве целых чисел Z и определяется как a ≡ b (mod 4), что читается «a конгруэнтно b по модулю 4» и означает, что разность a – b делится нацело на 4, или, иначе говоря, a при делении на 4 имеет такой же остаток, что и b при делении на 4. R4 является отношением эквивалентности на Z и порождает 4 класса эквивалентности в множестве Z / R4:
A0 = {…, – 8, – 4, 0, 4, 8, …},
A1 = {…, – 7, – 3, 1, 5, 9, …},
A2 = {…, – 6, – 2, 2, 6, 10, …},
A3 = {…, – 5, – 1, 3, 7, 11, …}.
2.9. Отношение частичного порядка
Отношение R на множестве S называется частично упорядоченным (или частичным порядком), если оно рефлексивно, антисимметрично и транзитивно.
1) Для каждого а ∈ S, (a, a) ∈ R.
2) Если (a, b) ∈ R и (b, a) ∈ R, то a = b.
3) Если (a, b) ∈ R и (b, c) ∈ R, то (a, c) ∈ R.
Множество, на котором определен частичный порядок R, называется частично упорядоченным множеством.
Пример 2.17.
(a) Отношение ≤ на множестве вещественных чисел R рефлексивно, антисимметрично и транзитивно, поэтому оно является отношением частичного порядка.
(b) Отношение включения множеств ⊆ является частичным порядком, поскольку выполняются все три свойства:
1) а ⊆ А, для любого множества А (рефлексивность);
2) если А ⊆ В и В ⊆ А, то тогда А = В (антисимметричность);
3) если А ⊆ В и В ⊆ С, то тогда А ⊆ С (транзитивность).
(с) Отношение «a делит b» является отношением частичного порядка на множестве положительных целых чисел N. Однако если это отношение определить на множестве целых чисел Z, то оно не будет отношением частичного порядка, поскольку нарушено свойство антисимметричности, например 5 | – 5 (5 является делителем – 5) и – 5 | 5 (и – 5 является делителем 5), но 5 × – 5.
Отношение R на множестве S называется называют частичным порядком, потому что оно может выполняться не для всех пар декартова произведения S × S. Если оно выполняется для всех пар, то тогда оно называется линейно упорядоченным, или цепью.
В примере 2.17(а) отношение не только частично упорядочено, но и является цепью. Отношение включения множеств (b) является частично упорядоченным, но не является цепью.
2.10. Решенные задачи
Произведение множеств
2.1. Даны множества A = {a, b, c}и B = {1, 2, 3 }. Найти декартово произведение следующих множеств
(a) А × В, (b) B × A, (c) A × A.
(a) Элементами А × В являются все упорядоченные пары (a, b), где a ∈ A и b ∈ B.
А × В = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3)}.
(b) Элементами B × A являются все упорядоченные пары (b, a), где b ∈ B и a ∈ A.
B × A = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)}.
(c) Элементами A × A являются все упорядоченные пары (x, y), где x, y ∈ A.
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}.
Число пар в каждом произведении равно произведению числа элементов обеих множеств этого произведения.
2.2. Доказать, что если А ⊆ Y и B ⊆ Z, то A × B ⊆ Y × Z.
Рассмотрим произвольную пару (a, b) из прямого произведения A × B, т. е. пусть (a, b) ∈ A × B. Тогда a ∈ A и b ∈ B. Поскольку А ⊆ Y, то тогда a ∈ Y, а поскольку B ⊆ Z, то тогда b ∈ Z. Из этого следует, что (a, b) ∈ Y × Z. Иначе говоря, любая пара из A × B принадлежит также и Y × Z, поэтому A × B ⊆ Y × Z.
2.3. Пусть A = {1, 2, 3}, B = {a, b, c, d}, C = {b, c, d, e}. Найти A × (B ∩ C) и (A × B) ∩ (A × C).
Найдем B ∩ C = {b, c, d}, тогда
A × (B ∩ C) = {(1, b), (1, c), (1, d), (2, b), (2, c), (2, d), (3, b), (3, c), (3, d)}.
Найдем далее.
A × B = {(1, a), (1, b), (1, c), (1, d), (2, a), (2, b), (2, c), (2, d), (3, a), (3, b), (3, c), (3, d)}.
A × C = {(1, b), (1, c), (1, d), (1, e), (2, b), (2, c), (2, d), (2, e), (3, b), (3, c), (3, d), (3, e)}.
Найдем теперь пересечение этих множеств.
(A × B) ∩ (A × C) = {(1, b), (1, c), (1, d), (2, b), (2, c), (2, d), (3, b), (3, c), (3, d)}.
2.4. Доказать, что декартово произведение множеств дистрибутивно относительно операции пересечения множеств
A × (B ∩ C) = (A × B) ∩ (A × C).
A × (B ∩ C) = {(x, y): x ∈ A и y ∈ B ∩ C} = {(x, y): x ∈ A, y ∈ B и x ∈ A, y ∈ C} = {(x, y): (x, y) ∈ A × B и (x, y) ∈ A × C} = (A × B) ∩ (A × C).
2.5. Доказать, что для любого непустого конечного множества А и универсального множества U выполняется
Ø × А = Ø.
Предположим противное, что Ø × А не пусто и имеется элемент (x, a) ∈ Ø × А. Тогда Ø × А = {(x, a): (x, a) ∈ Ø × А} = = {(x, a): x ∈ Ø и x ∈ A}. Это предположение приводит к противоречию, поскольку оказывается, что пустое множество Ø имеет элемент х, что невозможно. Поэтому Ø × А = Ø.
2.6. Все рассмотренные ранее отношения строились для пар элементов, т. е. были бинарными отношениями. Однако существуют отношения, образованные из большего числа элементов. Если таких элементов n, то отношения называют n-арными отношениями, т. е. для любого множества S подмножество произведения Sn называется n-арными отношением на S и, в частности, подмножество множества S3 называется тернарным отношением на S.
Пусть А = {1, 2, 3}, B = {4, 5, 6}, C = {7, 8}. Найти A × B × C.
Декартово произведение A × B × C содержит все упорядоченные тройки (a, b, c), где a ∈ A, b ∈ B и c ∈ C. Эти тройки представлены в виде дерева на рис. 2.11, при этом n(A × B × C) = n(A) · n(B) · n(C) = = 3 · 3 · 2 = 27.
Рис. 2.11
Отношения и их матрицы и графы
2.7. Пусть А = {1, 2, 3, 4} и B = {x, y, z}. Найти количество отношений из А в В.
Декартово произведение A × B имеет 4 × 3 = 12 элементов. Поэтому имеется 212 = 4096 подмножеств A × B и, следовательно, 4096 отношений из А в В.
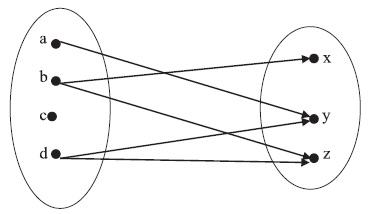
2.8. Имеется множество A = {a, b, c, d} и множество B = {x, y, z}, а также отношение R из А в В.
R = {(a, y), (b, x), (b, z), (d, y), (d, z)}.
(a) Нарисовать стрелочную диаграмму R.
(b) Найти матрицу отношения R.
(c) Найти обратное отношение R-1.
(d) Найти область определения и область значений R.
(e) Сечение по элементу d ∈ А отношения R.
(f) Фактор-множество множества В по отношению R.
(а) Стрелка из а ∈ А в b ∈ В должна присутствовать, если (a, b) ∈ R.
Рис. 2.12
(b) Строки матрицы определяются элементами из А, столбцы из В. Элемент матрицы, стоящий на пересечении i-й строки и j-го столбца равен 1, если определяемые им элементы ai ∈ А и bj ∈ В образуют пару (ai, bj) ∈ R и равен 0 в противном случае.
(с) Обратное отношение:
R-1 = {(y, a), (x, b), (z, b), (y, d), (z, d)}.
Чтобы получить диаграмму обратного отношения, надо поменять направления всех стрелок на противоположные на рис. 2.12.
(d) Область определения отношения R состоит из первых элементов всех пар, входящих в R, и это будет множество {a, b, d}. Область значений образована вторыми элементами пар для R, и это множество {x, y, z}.
(e) Сечением по элементу d ∈ А отношения R будет множество {y, z}.
(f) Фактормножество множества В по отношению R:
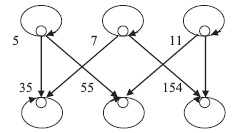
2.8. Имеется множество A = {5, 7, 11, 35, 55,154} и отношение R на А, которое означает, что «x делит y» и записывается обычно x | y. Иначе говоря, x делит y, если при делении y на x остаток равен 0, т. е. существует такое целое число z, называемое частным, что x · y = z.
(a) Записать R в виде упорядоченных пар.
(b) Нарисовать ориентированный граф отношения R.
(c) Найти обратное отношение R-1 и дать его словесное описание.
(a) Найдем все пары (x, y) ∈ R, в которых x является делителем y.
R = {(5, 5), ((5, 35), (5, 55), (7, 7), (7, 35), (7, 154), (11, 11), (11, 55), (11, 154), (35, 35), (55, 55), (154, 154)}.
(b) Орграф R представлен на рис. 2.13.
Рис. 2.13
(с) Обратное отношение состоит из пар:
R-1 = {(5, 5), ((35, 5), (55, 5), (7, 7), (35, 7), (154, 7), (11, 11), (55, 11), (154, 11), (35, 35), (55, 55), (154, 154)}. Словесное описание для (x, y) ∈ R-1 выражается следующим образом: «x кратно y».
2.9. Пусть R и S являются отношениями на X = {a, b, c}.
R = {(a, a), (a, b), (b, c), (a, c)}, S = {(a, a), (a, b), (b, a), (b, c), (b, b)}.
Найти (a) R ∩ S, R ∪ S, RC,
(b) R ○ S,
(c) S2 = S ○ S.
(a) Рассмотрим множество пар R и S и выберем пересечение и объединение из этих пар. Чтобы найти дополнение RC, необходимо знать универсальное множество, которым в данном случае является декартово произведение А × А.
R ∩ S = {(a, a), (a, b), (b, c)},
R ∪ S = {(a, a), (a, b), (b, c), (a, c), (b, a), (b, b)},
RC = {(b, a), (b, b), c, c), c, a)}.
(b) Для каждой пары (a, b) из R, найдем все пары (b, c) из S и получим все пары (а, c) ∈ R ○ S:
R ○ S = {(a, a), (a, b), (a, c)}.
(c) По аналогии с (b) для каждой пары (a, b) из R найдем все пары (b, c) также из R:
S2 = S ○ S = {(a, a), (a, b), (a, c)}.
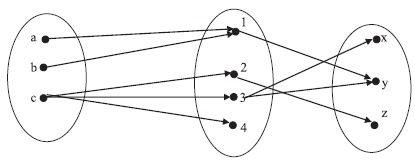
2.10. Дано: A = {a, b, c}, B = {1, 2, 3, 4}, C = {x, y, z}. Имеются отношения R и S из A в B и из B в C соответственно.
R = {(a, 1), (b, 1), (c, 2), (c, 3), (c,4)}, S = {(1,y), (2, z), (3, x), (4, z)}.
(а) Найти композицию отношений R ○ S.
(b) Найти матрицы MR,MS и MR ○ S для отношений R, S и R ○ S соответственно. Сравнить матрицу MR ○ S с матрицей произведения MR на MS.
(а) На рис. 2.14 показана стрелочная диаграмма отношений R и S. Чтобы найти композицию этих отношений, надо построить все пути для каждого элемента из множества А в множество С. Например, для элемента a существует путь a → 1 → y, поэтому (a, y) ∈ R ○ S.
Рис. 2.14
R ○ S={(a, y), (b, y), (c, x), (c, z)}.
Найдем матрицы для каждого из отношений R, S и R ○ S.
Найдем теперь произведение матриц MR и MS.
Матрицы MR ○ S и MRMS имеют одни и те же нулевые элементы, поэтому если в произведении матриц MRMS заменить все элементы большие 1 на 1, то мы получим матрицу композиции отношений MR ○ S.
Свойства отношений
2.11. Дано множество А = {1, 2, 3, 4, 5} и отношение R на А.
R = {(1, 2), (2, 1), (3, 3), (3, 4), (3, 5), (4, 5), (5, 5)}.
(a) Нарисовать орграф для R.
(b) Определить свойства R.
(a) Орграф представлен на рис. 2.15
Рис. 2.15
(b) R не рефлексивно, поскольку нет, например, пары (1, 1), т. е. (1, 1) ∉ R.
R не симметрично, например, (3, 4) ∈ R, но (4, 3) ∉ R.
R не антисимметрично, потому что (1, 2) ∈ R и (2, 1) ∈ R, но 1≠2.
R транзитивно, поскольку (3, 4) ∈ R, (4, 5) ∈ R и (3, 5) ∈ R.
2.12. Имеются следующие отношения на множестве A = {1, 2, 3, 4 }:
R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 2), (4, 4)},
S = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3), (3, 4), (4, 4)},
T = {(1, 2), (1, 3), (2, 2), (2, 3), (4, 3)},
Ø = пустое отношение,
A × A = универсальное отношение.
Определить, какие из этих отношений на А: (a) рефлексивны, (b) симметричны, (c) антисимметричны, (d) транзитивны.
(a) Рефлексивны только S и A × A. Отношение Ø не рефлексивно, R не рефлексивно, потому что не содержит пары (3, 3), T не рефлексивно, потому что нет пар (1, 1), (3, 3) и (4, 4).
(b) Симметричны отношения R, Ø и A × A. S не симметрично, потому что есть пара (1, 2), но нет пары (2, 1). По этой же причине не симметрично отношение T.
(c) Антисимметричны все отношения, кроме R, которое имеет (1, 2) ∈ R и (2, 1) ∈ R, но 1 ≠ 2.
(d) Транзитивны отношения T, Ø и A × A. R не транзитивно, потому что (1, 2) ∈ R и (2, 3) ∈ R, но (1, 3) ∉ R, S не транзитивно так как (1, 3) ∈ R и (3, 4) ∈ R, но (1, 4) ∉ R.
2.13. Пусть имеются следующие отношения на множестве N. Найти их свойства.
(a) (a, b) ∈ R1, если a ∈ N, b ∈ N и число (a + b) является четным.
(b) (a, b) ∈ R2, если a ∈ N, b ∈ N и число (a + b) является нечетным.
(c) (a, b) ∈ R3, если a ∈ N, b ∈ N и
является правильной дробью
(d) (a, b) ∈ R4, если a ∈ N, b ∈ N и a · b является степенью числа три.
(a) R1 рефлексивно, поскольку (а + а) = 2 · а и четно для любого а, симметрично, поскольку если (a + b) четно, то четно и (b + a). R1 не антисимметрично, так как 3 ≠ 5, но 3 + 5 = 5 + 3 = 8 и является четным числом. Транзитивность следует из того факта, что сумма любых двух четных чисел четна и сумма любых двух нечетных чисел также четна. Например, (1 + 3) четно и (3 + 5) четно и (1 + 5) также четно.
(b) R2 не рефлексивно, но симметрично, поскольку если (a + b) нечетно, то (b + a) также нечетно. R2 не антисимметрично, например (2 + 3) = 5 нечетно и (3 + 2) нечетно, но 2 ≠ 3. Отношение R2, кроме того, не транзитивно, например (2, 1) ∈ R2 и (1, 4) R2, но (2, 4) ∉ R2.
(c) R3 не рефлексивно, поскольку
= 1 и не является правильной дробью. Это отношение также не симметрично, если (1, 2) ∈ R3 поскольку
является правильной дробью, то (2, 1) ∉ R3, так как
не является правильной дробью. R3 антисимметрично, потому что для любых a ∈ N, b ∈ N, если (a, b) ∈ R3, то (b, a) ∉ R3. Отношение R3 транзитивно.
(d) Отношение R4 не рефлексивно, например 2 ∈ N, но (2, 2) ∉ R4, потому что 2 × 2 = 4 и не является степенью тройки R4 симметрично и транзитивно, но не антисимметрично.
2.14. Дать примеры отношений R на А = {1, 2, 3, 4} со следующими свойствами:
(a) R – антисимметрично, но не симметрично.
(b) R – антисимметрично и симметрично.
(c) R – только транзитивно.
Возможно несколько различных примеров для каждого случая. Ниже представлен один из возможных вариантов.
(a) R = {(1, 2), (1, 4), (2, 3)}.
(b) R = {(1, 1), (2, 2), (4, 4)}.
(c) R = {(1, 2), (1, 3), (1, 4), (2, 3), (3, 3), (4, 1)}.
2.15. Отношение R антисимметрично, если всякий раз, когда (a, b) ∈ R и (b, a) ∈ R, то тогда a = b. Следует ли из этого, что если отношение антисимметрично, то оно рефлексивно?
Нет не следует, потому что определение антисимметричности не требует, чтобы это условие выполнялось для всех пар отношения R.
2.16. Если отношение R транзитивно, то для всех a, b, c ∈ A таких, что если (a, b) ∈ R и (b, с) ∈ R, то тогда (a, с) ∈ R. Заменим с на а, тогда, по определению транзитивности, из того, что (a, b) ∈ R и (b, а) ∈ R следует, что (a, a) ∈ R и, значит, если отношение транзитивно, то оно и рефлексивно. В чем ошибка этого утверждения?
Ошибка в том, что все три элемента a, b, c ∈ A в определении транзитивности должны быть различны.
2.17. Дать пример двух симметричных отношений R и S на А = {1, 2, 3}, композиция которых R ○ S:
(a) симметрична,
(b) не симметрична.
(a) R = {(1,2), (2, 1), (3, 2), (2, 3)}, S = {(1, 1), (2, 2), (1, 3), (3, 1)}.
R ○ S = {(1,2), (2, 1), (3, 2), (2, 3)}.
(b) R = {1, 2), (2, 1)}, S={(2, 3), (3, 2)}.
R ○ S = {(1, 3)}.
2.18. Пусть R и S отношения на множестве А. Показать, что если T является пересечением этих отношений Т = R ∩ S и если отношения R и S симметричны и транзитивны, то отношение Т также симметрично и транзитивно.
Пусть имеется (a, b) ∈ T, тогда (a, b) ≈ ∈ R и (a, b) ∈ S и поскольку эти отношения симметричны, имеется пара (b, a) ∈ R и (b, a) ∈ S. Но тогда пара (b, a) ∈ T, поскольку Т представляет собой пересечение элементов S и T и поэтому Т также симметрично. Аналогично, если (a, b) ∈ T и (b, c) ∈ T, то (a, b) ∈ R и (b, c) ∈ R, а поскольку R транзитивно, то (a, c) ∈ R и также (a, c) ∈ S Поскольку Т является пересечением R ∩ S, то Т должно также содержать (a, c), т. е. (a, c) ∈ Т и, значит, Т транзитивно.
2.19. Пусть имеется множество A = {1, 2, 3, 4} и отношение R на A.
R = {(1, 2), (2, 2), (2, 3), (3, 4)}.
Найти:
(a) рефлексивное замыкание (R),
(b) симметричное замыкание (R),
(с) транзитивное замыкание (R).
(a) Для нахождения рефлексивного замыкания на R надо добавить те пары диагонального отношения, которых нет в R.
Рефлексивное замыкание R = R ∪ {(1, 1), (3, 3), (4, 4)} =
= {(1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4), (4, 4)}.
(b) Для симметричного замыкания надо добавить пары из R-1, которых нет в R.
Симметричное замыкание R = R ∪ {(2, 1), (3, 1), (4, 3)}.
(c) Транзитивное замыкание на R можно получить, если найти объединение R с R2, R3 и R4, поскольку А имеет 4 элемента.
R2 = R ○ R = {(1, 2), (1, 3), (2, 2), (2, 3), (2, 4)}.
R3 = R ○ R ○ R = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.
R4 = R ○ R ○ R ○ R = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.
Транзитивное замыкание R = R ∪ R2 ∪ R3 ∪ R4 =
= {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 4)}.
Отношение эквивалентности и разбиения