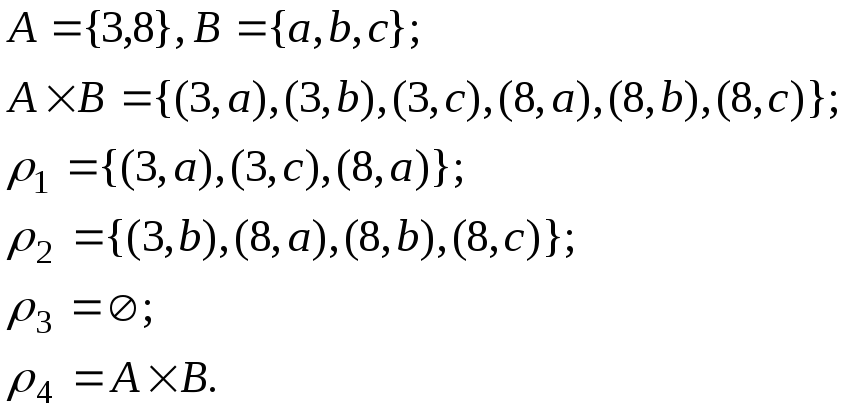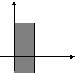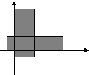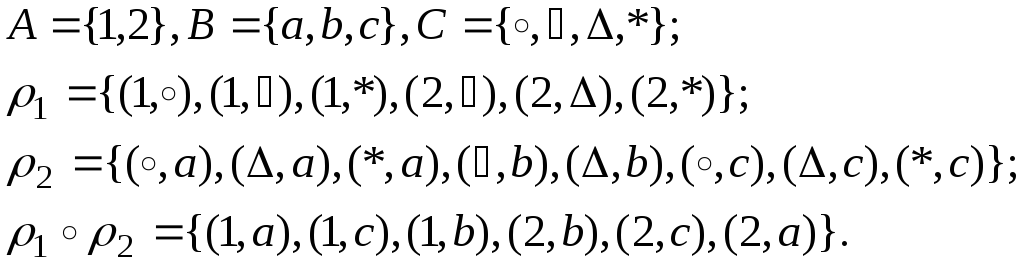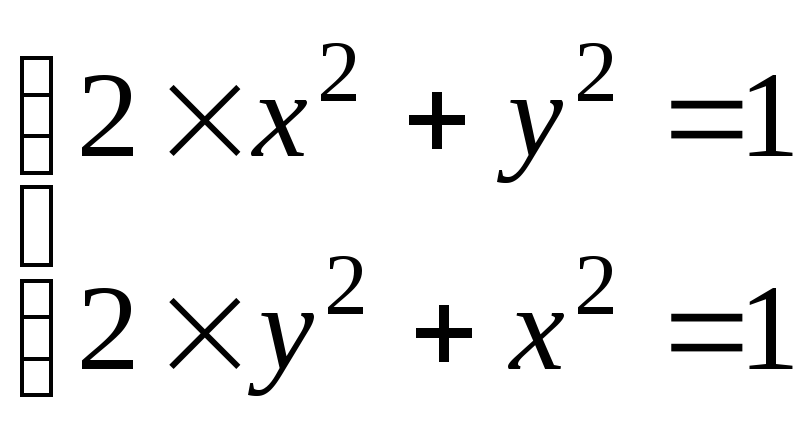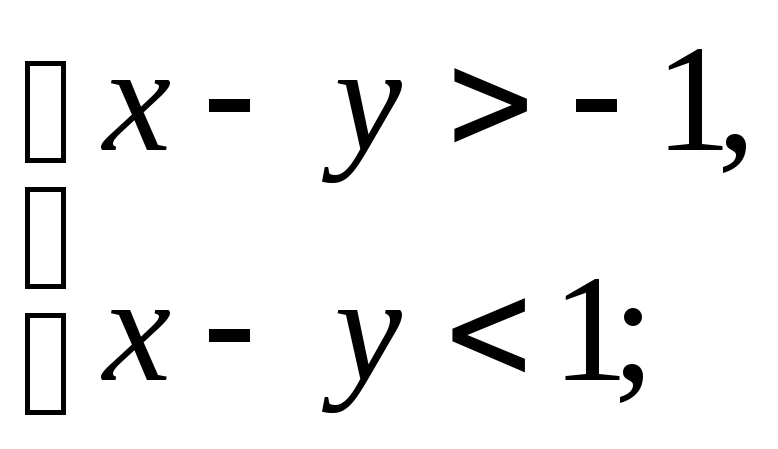Как найти композицию бинарных отношений

Операции над соответствиями на множествах

Поскольку соответствия можно считать множествами, то все операции над множествами (пересечение, объединение, разность, дополнение и т.д.) можно применить и к соответствиям. Заметим, что, говоря о дополнении соответствия из в , мы имеем в виду дополнение до универсального соответствия из в , т.е. до декартова произведения Atimes B . Естественно, что и равенство соответствий можно трактовать как равенство множеств.

В то же время на соответствия можно распространить операции, определяемые для отображений. Мы рассмотрим здесь две такие операции.

Композиция соответствии. Следуя аналогии с композицией отображнений, композицией (произведением) соответствий rhosubseteq Atimes B и sigmasubseteq Btimes C называют соответствие

rhocircsigma= bigl{(x,y)colon, (exists zin B)((x,z)inrho)land ((z,y)insigma)bigr}.

(1.3)

Поясним построение композиции двух соответствий. Обратимся сначала к отображениям (как частным случаям соответствий). Пусть заданы отображения (возможно, частичные): из в и из в . Композиция fcirc g определяется как отображение из в , задаваемое формулой y=g(f(x)) . Тем самым задается график отображения fcirc g , т.е. множество упорядоченных пар (x,y) , таких, что . При этом упорядоченная пара (x,y) будет принадлежать графику отображения fcirc g , если и только если найдется элемент zin b , такой, что z=f(x) и y=g(z) . Таким образом, график композиции отображений и есть

fcirc g=bigl{(x,y)colon, (exists z)(z=f(x),, y=g(z))bigr}= bigl{(x,y)colon, y=g(f(x))bigr}.

(1.4)

Необходимо заметить, что запись gcirc f(x) означает g(f(x)) , т.е. отображения в композиции пишутся в порядке, обратном тому, в каком они применяются. Мы же будем везде использовать запись fcirc g , полагая, что fcirc g(x)=g(f(x)) и порядок записи отображений в композиции совпадает с порядком их применения. Это обусловлено тем, что композиция отображений определяется нами как частный случай композиции соответствий, при записи которой естественным оказывается именно такой порядок.

Легко видеть, что (1.4) есть частный случай (1.3). Отметим, что при построении композиции отображений обычно предполагают, что пересечение области значений отображения и области определения отображения не пусто (R(f)cap D(g)ne varnothing) , поскольку в противном случае композиция была бы пуста. Для отображений, не являющихся частичными, R(f)subseteq D(g) , так как D(g)=B . Поэтому в данном случае пересечение R(f)cap D(g) всегда не пусто.

Полезно отметить также, что если и — биекции, то и композиция их тоже будет биекцией.

Вернемся к рассмотрению композиции соответствий rhocircsigma . Полагая, что область определения D(rho) соответствия rho не пуста, возьмем произвольный элемент xin D(rho) . Пусть сечение rho(x)subseteq B соответствия rho не пусто и найдется такой элемент zinrho(x) , что сечение sigma(z)subseteq C также не пусто. Тогда непустое множество {(x,t)colon, tinsigma(z)} будет подмножеством сечения соответствия rhocircsigma в точке . Сечением соответствия в точке будет непустое в силу сделанных предположений множество всех таких упорядоченных пар (x,t)in Atimes C , что xin D(rho) , а tinsigma(z) для некоторого zinrho(x) . Говоря неформально, нужно перебрать все элементы из сечения rho(x) . Таким образом, различие в построении композиции соответствий и композиции отображений заключается в том, что «промежуточный» элемент z в общем случае не единственный и каждому такому элементу также ставится в соответствие не единственный элемент yin C .

Пример 1.8. Соответствие rho возьмем из примера 1.3. Соответствие sigma зададим как соответствие из множества программ ${n_1,n_2 ,n_3, n_4, n_5}$ в множество заказчиков программного обеспечения ${Z_1,Z_2,Z_3,Z_4}$ . Пусть

$sigma=bigl{(n_1,Z_3),, (n_1,Z_4),, (n_2,Z_1),, (n_2,Z_1),, (n_3,Z_2),, (n_4,Z_4),, (n_5,Z_3)bigr}.$

Рассмотрим процесс построения композиции соответствий rho и sigma . Начнем с элемента . Имеем

$rho(I)={n_1,n_3,n_5},quad sigma(n_1)={Z_3,Z_4},quad sigma(n_3)={Z_2},quad sigma(n_5)={Z_5}.$

Отсюда получаем сечение композиции по элементу

$sigma(n_1)cupsigma(n_3)cupsigma(n_5)= {Z_2,Z_3,Z_4}.$

Рассуждая аналогично, получим $(rhocircsigma)(P)={Z_1,Z_4}$ и $(rhocircsigma)(C)={Z_1,Z_3}$ .

Построение графа композиции rhocircsigma проиллюстрировано на рис. 1.3.

Построение графа композиции соответствий

Отметим, что область определения композиции соответствий содержится в области определения первого соответствия, а область значений композиции соответствий — в области значений второго соответствия. Из приведенных рассуждений следует, что для того, чтобы композиция соответствий была отлична от пустого соответствия, необходимо и достаточно, чтобы пересечение области значений первого соответствия и области определения второго соответствия было не пусто.

К определению композиции соответствий можно подойти с более общих позиций. Пусть rho subseteq Atimes B и sigma subseteq Ctimes D . При этом на множества A,,B,,C и априори не накладывается никаких органичений. Композиция rhocircsigma соответствий rho и sigma в этом случае также определяется соотношением (1.3). Чтобы такая композиция была отлична от пустого соответствия, необходимо и достаточно выполнение условия R(rho)cap D(sigma)ne varnothing . В частности, rhocircsigma=varnothing всякий раз, когда Bcap C=varnothing .

Пример 1.9. Рассмотрим соответствие tau={(1,a),(2,a),(3,d)} из множества A={1;2;3} в множество B={a,b,d} и соответствие varphi= {(b,e), (b,f), (c,f)} из множества C={b,c,d} в множество D={e,f} . В данном случае Bcap Cnevarnothing , но taucircvarphi=varnothing , поскольку

R(tau)={a,d},qquad D(varphi)={b,c},qquad R(tau)cap D(varphi)=varnothing.

Заметим, что композиция соответствий rho subseteq Atimes B и sigma subseteq Ctimes D не коммутативна, т.е. в общем случае rhocircsigmane sigmacircrho , поскольку rhocircsigma subseteq Atimes D , а sigmacircrho subseteq Ctimes B .

Композиция бинарного отношения на множестве

Бинарное отношение на множестве является частным случаем соответствия. Для двух бинарных отношении rho и sigma , заданных на множестве , их композиция rhocircsigma (1.3) как соответствий является бинарным отношением на том же множестве . В этом случае говорят о композиции бинарных отношений на множестве .

Композицию rhocircrho бинарного отношения rho на некотором множестве с самим собой называют квадратом бинарного отношения rho и обозначают rho^2 .

Рассмотрим пример построения композиции бинарных отношений на множестве и покажем, что в общем случае для двух бинарных отношений tau и varphi также имеет место неравенство taucircvarphine varphicirctau , хотя обе композиции, в отличие от аналогичных композиций двух произвольных соответствий, заданы на одном и том же множестве.

Построение композиции бинарных отношений

Пример 1.10. а. Зададим на множестве A={1,2,3,4} бинарные отношения tau,,varphi и найдем композицию taucircvarphi , если

tau=bigl{(x,y)colon, x+1<ybigr},quad varphi=bigl{(x,y)colon, |x-y|=2bigr}.

Имеем tau(1)={3;4},~ varphi(3)={1} и varphi(4)={2} . Следовательно, (taucircvarphi)(1)= varphi(3)cupvarphi(4)={1;2} . Далее tau(2)={4},~ varphi(4)={2} и (taucircvarphi)(2)={2} . Так как tau(3)= varphi(4)= varnothing , то в итоге получим taucircvarphi={(1;1),(1;2),(2;2)} . Построение композиции проиллюстрировано на рис. 1.4,а.

Найдем композицию varphicirctau . Поскольку varphi(1)={3} , а tau(3)=varnothing , то (varphicirctau)(1)=varnothing . Аналогично varphi(2)={4} , а tau(4)=varnothing , поэтому (varphicirc tau)(2)= varnothing . Далее varphi(3)={1},~ tau(1)={3;4} , поэтому (varphicirc tau)(3)= {3;4} , а varphi(4)={2},~ tau(2)={4} и (varphicirc tau)(4)= {4} . Построение композиции проиллюстрировано на рис. 1.4,б.

Легко видеть, что taucircvarphinevarphicirctau .

б. Пусть отношение rho на множестве действительных чисел определено как функция y=ax+b . Найдем квадрат этого отношения (линейной функции от одного переменного).

Согласно (1.4), это будет функция , такая, что h(x)=a(ax+b)+c , то есть h(x)=a^2x+(ab+c) . Это тоже линейная функция, но с другими коэффициентами.

Свойства композиции соответствий

Приведем некоторые свойства композиции соответствий:

1) rhocirc(sigmacirctau)= (rhocircsigma)circtau ;
2) для любого соответствия rho имеет место rhocirc varnothing= varnothingcirc tau= varnothing ;
3) rhocirc(sigmacuptau)= (rhocircsigma)cup (rhocirctau) ;
4) для любого бинарного отношения на множестве имеет место равенство rhocirc operatorname{id}Acirc rho= rho .

Эти свойства нетрудно доказать методом двух включений. Рассмотрим в качестве примера доказательство свойства 3. Пусть некоторая упорядоченная пара (x,y) принадлежит композиции rhocirc(sigmacuptau) . Тогда, согласно (1.3), найдется такой элемент , что (x,z)inrho и (z,y)insigmacuptau . Последнее означает, что или (z,y)intau . Таким образом, для элемента имеем и или и . Первая альтернатива имеет место при (x,y)inrhocircsigma , а вторая — при (x,y)inrhocirctau , что означает (x,y)in rhocirc sigmacup rhocirc tau . Тем самым включение rhocirc (sigmacup tau)subseteq rhocirc sigmacup rhocirctau доказано.

Доказательство включения rhocirc sigmacup rhocirctau subseteq rhocirc (sigmacup tau) запишем коротко, используя логическую символику:

$begin{aligned} (x,y)in rhocircsigmacup rhocirctau &Rightarrow (exists u)bigl(((x,u)inrho)land ((u,y)insigma)bigr)lor (exists v)bigl(((x,v)inrho)land ((v,y)intau)bigr) Rightarrow \[2pt] &Rightarrow (exists z)bigl(((x,z)inrho)land (((z,y)insigma)lor ((z,y)intau))bigr) Rightarrow\[2pt] &Rightarrow (exists z)bigl(((x,z)inrho)land ((z,y)insigmacuptau)bigr) Rightarrow\[2pt] &Rightarrow (x,y)in rhocirc (sigmacuptau). end{aligned}$

В данном случае доказательства двух включений не совсем симметричны: элементы и во второй части доказательства не обязаны совпадать.

Замечание 1.4. В тождестве, выражающем свойство 3, нельзя вместо объединения поставить пересечение, так как в этом случае тождество нарушатся. Можно доказать, что сохранится лишь включение

rhocirc (sigmacap tau)subseteq rhocirc sigmacap rhocirctau,,

а обратное включение в общем случае не имеет места.

Анализ свойств 2 и 4 показывает, что роль пустого соответствия аналогична роли нуля при умножении чисел, а диагональ множества играет роль, аналогичную роли единицы, на множестве всех бинарных отношений на .

Обратное соответствие и его свойства

Соответствие, обратное к соответствию rho subseteq Atimes B , есть соответствие из в , обозначаемое $rho^{-1}$ и равное, по определению, $rho^{-1}= {(y,x)colon, (x,y)inrho}$ .

Для соответствия tau из примера 1.3

$tau^{-1}= bigl{(n_1,I),, (n_2,P),, (n_2,C),, (n_3,I),, (n_4,P),, (n_5,I),, (n_5,C)bigr}.$

Обратное соответствие обладает следующими легко проверяемыми свойствами:

1) $(rho^{-1})^{-1}=rho$ ;
2) $(rhocircsigma)^{-1}=sigma^{-1}circrho^{-1}$ .

Для бинарного отношения rho на множестве обратное соответствие есть бинарное отношение на том же множестве. В этом случае говорят о бинарном отношении $rho^{-1}$ на множестве , обратном к rho .

Заметим, что соответствия $rhocircrho^{-1}$ и $rho^{-1}circrho$ в общем случае не совпадают. Даже для бинарного отношения rho на множестве

$Arhocircrho^{-1}ne rho^{-1}circrho$ , а также $rhocirc rho^{-1}ne operatorname{id}A$ и $rho^{-1}circ rhone operatorname{id}A$ .

Например, для бинарного отношения rho={(3;1), (4;1), (4;2)} на множестве A={1;2;3;4} графы самого отношения, обратного отношения $rho^{-1}$ , композиций $rhocircrho^{-1}$ и $rho^{-1}circrho$ представлены на рис. 1.5.

Графы бинарного отношения, обратного отношения и композиций

Если fcolon Ato B — отображение, то оно является соответствием. Обратное к соответствие из в в общем случае не является отображением. Действительно, соответствие $f^{-1}$ , обратное к , состоит из всех упорядоченных пар вида (f(x),x),, xin A . Поскольку в общем случае могут найтись такие два различных элемента и , что f(x)= f(x') , то соответствие $f^{-1}$ в общем случае не будет функционально по второй компоненте и поэтому не будет отображением. Если отображение инъективно, то обратное соответствие есть частичное отображение из в . Если отображение биективно, то обратное соответствие является отображением из в , причем имеют место равенства

$fcirc f^{-1}=operatorname{id}A,,qquad f^{-1}circ f= operatorname{id}B,.$

Отображение $f^{-1}$ в этом случае называют отображением, обратным к .

Ограничение соответствия

Пусть rho subseteq Atimes B — соответствие из в и C subseteq A,~ D subseteq B . Ограничением соответствия rho на подмножества и (или (C,D) -ограничением соответствия rho ) называется соответствие из в , обозначаемое $rhobig|_{C,D}$ , такое, что

$(x,y)in rhobig|_{C,D}~ Leftrightarrow~ bigl((x,y)inrhobigr)land (xin C)land (yin D).$

Таким образом, (C,D) -ограничение соответствия rho есть «то же самое» соответствие rho , но из последнего берутся только упорядоченные пары, первая компонента которых принадлежит подмножеству , а вторая — подмножеству . Можно записать

$rhobig|_{C,D}= rhocap (Ctimes D).$

Так, «малый» арксинус, т.е. функция y=arcsin{x} , есть ограничение «большого» арксинуса y=operatorname{Arcsin}x , который является соответствием на подмножества [-1;1] и $left[-frac{pi}{2};frac{pi}{2}right]$ .

Рассмотрим некоторые важные частные случаи ограничений соответствий (в частности, бинарных отношений и отображений).

Всякое (C,D) -ограничение соответствия rho subseteq Atimes B будем называть сужением соответствия rho на подмножество (коротко — C-сужением соответствия rho ), а всякое (C,rho(C)) -ограничение соответствия rho — строгим сужением соответствия rho на подмножество (строгим C-сужением соответствия р). C-сужения соответствия rho будем обозначать $rhobig|_{C}$ , а строгое сужение — $rhobig|_{circ C}$ соответственно.

Полезно заметить, что для любого отображения fcolon Ato B строгое сужение $fbig|_{circ A}$ есть сюръекция на f(A) . Если, сверх этого, является инъекцией, то $fbig|_{circ A}$ есть биекция на f(A) . Допуская некоторую вольность речи, можно сказать, что любое отображение сюръективно отображает свою область определения на свою область значений, в частности, любая инъекция устанавливает взаимно однозначное соответствие между областью определения и областью значений. Так, функция y=sin{x} сюръективно отображает множество mathbb{R} всех действительных чисел на отрезок [-1;1] , а любая показательная функция биективно отображает на подмножество всех положительных действительных чисел.

Для бинарного отношения rho subseteq A^2 и любого подмножества M subseteq A (M,M)-ограничение бинарного отношения называют ограничением бинарного отношения rho на подмножество и обозначают $rhobig|_{M}$ . Можно записать $rhobig|_{M}=rhocap M^2$ .

Рассмотрим, например, отношение естественного порядка leqslant на множестве действительных чисел. Тогда отношение $leqslantbig|_{mathbb{Z}}= bigl{(m,n)colon, m leqslant n;~ m,ninmathbb{Z}bigr}$ есть ограничение этого порядка на подмножество целых чисел. Но ни в коем случае нельзя путать это отношение с -сужением отношения ! Это последнее состоит из всех таких упорядоченных пар (m,x) , что minmathbb{Z},, xinmathbb{R} и mleqslant x , т.е. вторая компонента пары может быть произвольным действительным числом, не меньшим заданного целого .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Бинарные отношения.

Пусть А и В – два произвольных
множества.

Определение 3. Бинарным
отношением

из множества А в
множество В называется
всякое подмножество прямого произведения
А на В; если А=В, то говорят
о бинарном отношении на множестве
А. Обозначение:

Пример 2.

Используют две формы записи принадлежности
некоторой упорядоченной пары заданному
бинарному отношению:

Инфиксная:

Префиксная:

По аналогии с бинарным отношением вводят
понятие n – арного
отношения 
произвольного подмножества упорядоченных
n – ок, выбранных из
прямого произведения данных n
множеств.

Пример 3.

M – множество;

2^M– булеан
множества M;

бинарное отношение включения на

определяется так:

Определение 4. Множество
точек плоскости, координаты которых
(x,y),
образуют упорядоченные пары некоторого
бинарного отношения

называется графиком данного
бинарного отношения.

Пример 4.

1).

График

2).

График

Бинарные отношения – это множества, их
можно объединять, пересекать, дополнять
и т. д.

Пример 5.

1).

График

2).

График

Пусть

Определение 5. Областью
определения бинарного отношения
(обозначение:),
называется подмножество множества А
такое, что

Пусть

Определение 6. Областью
значения бинарного отношения
(обозначение:
),
называется подмножество множества В
такое, что

Пусть

Определение 7. Отношением,
обратным к отношению
,
называют подмножество прямого произведения
,
такое, что
.

Пример 6.

Определение 8. Дополнением
отношения

называют бинарное отношение, определяемое
как множество всех упорядоченных пар,
не входящих в
:

Пример 7.

Определение 9. Тождественным
отношением I
называют подмножество А² такое, что

Пример 8.

Определение 10. Универсальным
отношением U
называют само прямое произведение
множеств

Композиция отношений.

Пусть

Определение 11. Композицией
отношений

называют бинарное отношение из множества
А во множество В, определяемое
так:

Пример 9.

Пусть

— это отношение, заданное на множестве
А, тогда бинарное отношение

называется

.рефлексивным, если
.антирефлексивным, если
.симметричным, если
.антисимметричным, если
.транзитивным, если
.полным если

Пример 10.

Является ли

рефлексивным, антирефлексивным,
симметричным, антисимметричным, полным?

1).

нерефлексивно;

например,

2).

неантирефлексивно;

,
так как уравнение

имеет решения:

3).

несимметрично;

например,

4).

не антисимметрично.

Пусть

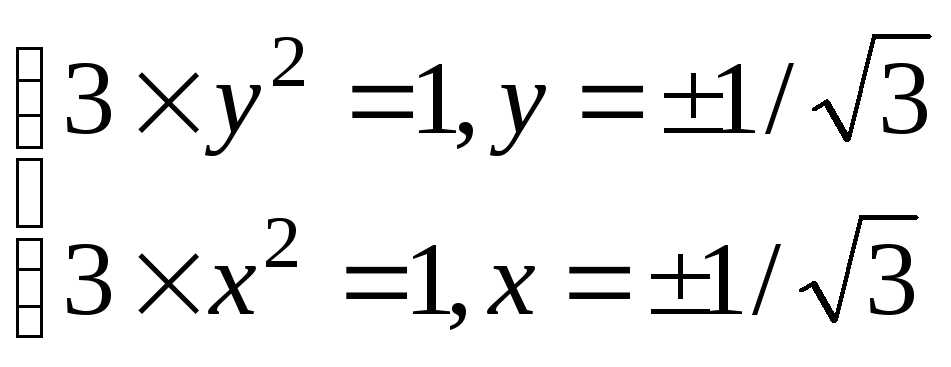
Тогда

5).

не транзитивно:

например

но

6).

не полное, что очевидно.

Пример 11.

1).

 рефлексивно.

2). Пусть

тогда

т.к. х, у – целые числа 
 антисимметрично.

Пусть

тогда

Значит

 транзитивно.

Если

то или

или

 полное отношение.

Теорема о свойствах бинарного отношения.

Пусть

 отношение на
множестве А(),
тогда справедливы следующие утверждения:

-
рефлексивно
;
 симметрично;
 транзитивно;
 антирефлексивно;
 антисимметрично;
 полно.

Доказательство.

1.

Пусть

 рефлексивно,
;

1.

Пусть
,
тогда

– рефлексивно.

2.

Пусть

 симметрично,
.

Пусть
.

Пусть
.
Значит,
.

2.

Пусть
.
Тогда

– симметрично.

3.

Пусть

 транзитивно,

и

Пусть
)
и (;

3.

Пусть
.
Пусть ()и
(—
транзитивно.

4.

Пусть

 антирефлексивно,
():;

4.

Пусть
:

 антирефлексивно.

5.

Пусть

 антисимметрично
():()
и
.
Если

и (),
то ()и
,
пересечение множеств

и

по парам, состоящих из разных элементов,
 пусто

эти множества в качестве общих могут
иметь только элементы вида
,
что и означает:
;

5.

Пусть

это означает, что в пересечение

могут входить только пары вида

если

и
,
то
.

6.

Пусть
-полно,
(,
):
()
или

Но
,обе
пары

и

принадлежат объединению:
;

Пусть
.
Если
,
то
.

Либо
.

Либо

— полно.

ЛЕКЦИЯ 7.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

In the mathematics of binary relations, the composition of relations is the forming of a new binary relation R; S from two given binary relations R and S. In the calculus of relations, the composition of relations is called relative multiplication,^[1] and its result is called a relative product.^[2]^: 40 Function composition is the special case of composition of relations where all relations involved are functions.

The word uncle indicates a compound relation: for a person to be an uncle, he must be the brother of a parent. In algebraic logic it is said that the relation of Uncle () is the composition of relations «is a brother of» () and «is a parent of» ().

Beginning with Augustus De Morgan,^[3] the traditional form of reasoning by syllogism has been subsumed by relational logical expressions and their composition.^[4]

Definition[edit]

If and are two binary relations, then
their composition is the relation

In other words, is defined by the rule that says if and only if there is an element yin Y such that (that is, and ).^[5]^: 13

Notational variations[edit]

The semicolon as an infix notation for composition of relations dates back to Ernst Schroder’s textbook of 1895.^[6] Gunther Schmidt has renewed the use of the semicolon, particularly in Relational Mathematics (2011).^[2]^: 40^[7] The use of semicolon coincides with the notation for function composition used (mostly by computer scientists) in category theory,^[8] as well as the notation for dynamic conjunction within linguistic dynamic semantics.^[9]

A small circle has been used for the infix notation of composition of relations by John M. Howie in his books considering semigroups of relations.^[10] However, the small circle is widely used to represent composition of functions which reverses the text sequence from the operation sequence. The small circle was used in the introductory pages of Graphs and Relations^[5]^: 18 until it was dropped in favor of juxtaposition (no infix notation). Juxtaposition is commonly used in algebra to signify multiplication, so too, it can signify relative multiplication.

Further with the circle notation, subscripts may be used. Some authors^[11] prefer to write $circ _{l}$ and $circ _{r}$ explicitly when necessary, depending whether the left or the right relation is the first one applied. A further variation encountered in computer science is the Z notation: circ is used to denote the traditional (right) composition, but ⨾ (U+2A3E ⨾ Z NOTATION RELATIONAL COMPOSITION) denotes left composition.^[12]^[13]

The binary relations are sometimes regarded as the morphisms in a category Rel which has the sets as objects. In Rel, composition of morphisms is exactly composition of relations as defined above. The category Set of sets is a subcategory of Rel that has the same objects but fewer morphisms.

Properties[edit]

Composition in terms of matrices[edit]

Finite binary relations are represented by logical matrices. The entries of these matrices are either zero or one, depending on whether the relation represented is false or true for the row and column corresponding to compared objects. Working with such matrices involves the Boolean arithmetic with and An entry in the matrix product of two logical matrices will be 1, then, only if the row and column multiplied have a corresponding 1. Thus the logical matrix of a composition of relations can be found by computing the matrix product of the matrices representing the factors of the composition. «Matrices constitute a method for computing the conclusions traditionally drawn by means of hypothetical syllogisms and sorites.»^[14]

Heterogeneous relations[edit]

Consider a heterogeneous relation that is, where and are distinct sets. Then using composition of relation with its converse ${displaystyle R^{textsf {T}},}$ there are homogeneous relations ${displaystyle RR^{textsf {T}}}$ (on ) and ${displaystyle R^{textsf {T}}R}$ (on ).

If for all xin A there exists some such that xRy (that is, is a (left-)total relation), then for all ${displaystyle x,xRR^{textsf {T}}x}$ so that ${displaystyle RR^{textsf {T}}}$ is a reflexive relation or ${displaystyle Isubseteq RR^{textsf {T}}}$ where I is the identity relation Similarly, if is a surjective relation then

${displaystyle R^{textsf {T}}Rsupseteq I={xIx:xin B}.}$

In this case ${displaystyle Rsubseteq RR^{textsf {T}}R.}$ The opposite inclusion occurs for a difunctional relation.

The composition ${displaystyle {bar {R}}^{textsf {T}}R}$ is used to distinguish relations of Ferrer’s type, which satisfy ${displaystyle R{bar {R}}^{textsf {T}}R=R.}$

Example[edit]

Let { France, Germany, Italy, Switzerland } and { French, German, Italian } with the relation given by aRb when is a national language of
Since both and is finite, can be represented by a logical matrix, assuming rows (top to bottom) and columns (left to right) are ordered alphabetically:

${displaystyle {begin{pmatrix}1&0&0\0&1&0\0&0&1\1&1&1end{pmatrix}}.}$

The converse relation ${displaystyle R^{textsf {T}}}$ corresponds to the transposed matrix, and the relation composition ${displaystyle R^{textsf {T}};R}$ corresponds to the matrix product ${displaystyle R^{textsf {T}}R}$ when summation is implemented by logical disjunction. It turns out that the matrix ${displaystyle R^{textsf {T}}R}$ contains a 1 at every position, while the reversed matrix product computes as:

${displaystyle RR^{textsf {T}}={begin{pmatrix}1&0&0&1\0&1&0&1\0&0&1&1\1&1&1&1end{pmatrix}}.}$

This matrix is symmetric, and represents a homogeneous relation on

Correspondingly, ${displaystyle R^{textsf {T}},;R}$ is the universal relation on hence any two languages share a nation where they both are spoken (in fact: Switzerland).
Vice versa, the question whether two given nations share a language can be answered using ${displaystyle R,;R^{textsf {T}}.}$

Schröder rules[edit]

For a given set the collection of all binary relations on forms a Boolean lattice ordered by inclusion Recall that complementation reverses inclusion:
${displaystyle Asubseteq B{text{ implies }}B^{complement }subseteq A^{complement }.}$
In the calculus of relations^[15] it is common to represent the complement of a set by an overbar: ${displaystyle {bar {A}}=A^{complement }.}$

If is a binary relation, let ${displaystyle S^{textsf {T}}}$ represent the converse relation, also called the transpose. Then the Schröder rules are

${displaystyle QRsubseteq Squad {text{ is equivalent to }}quad Q^{textsf {T}}{bar {S}}subseteq {bar {R}}quad {text{ is equivalent to }}quad {bar {S}}R^{textsf {T}}subseteq {bar {Q}}.}$

Verbally, one equivalence can be obtained from another: select the first or second factor and transpose it; then complement the other two relations and permute them.^[5]^: 15–19

Though this transformation of an inclusion of a composition of relations was detailed by Ernst Schröder, in fact Augustus De Morgan first articulated the transformation as Theorem K in 1860.^[4] He wrote^[16]

${displaystyle LMsubseteq N{text{ implies }}{bar {N}}M^{textsf {T}}subseteq {bar {L}}.}$

With Schröder rules and complementation one can solve for an unknown relation in relation inclusions such as

For instance, by Schröder rule ${displaystyle RXsubseteq S{text{ implies }}R^{textsf {T}}{bar {S}}subseteq {bar {X}},}$ and complementation gives ${displaystyle Xsubseteq {overline {R^{textsf {T}}{bar {S}}}},}$ which is called the left residual of by .

Quotients[edit]

Just as composition of relations is a type of multiplication resulting in a product, so some operations compare to division and produce quotients. Three quotients are exhibited here: left residual, right residual, and symmetric quotient. The left residual of two relations is defined presuming that they have the same domain (source), and the right residual presumes the same codomain (range, target). The symmetric quotient presumes two relations share a domain and a codomain.

Definitions:

Using Schröder’s rules, is equivalent to Thus the left residual is the greatest relation satisfying Similarly, the inclusion is equivalent to and the right residual is the greatest relation satisfying ^[2]^: 43–6

One can practice the logic of residuals with Sudoku.^{[further explanation needed]}

Join: another form of composition[edit]

A fork operator has been introduced to fuse two relations and into The construction depends on projections and understood as relations, meaning that there are converse relations ${displaystyle a^{textsf {T}}}$ and ${displaystyle b^{textsf {T}}.}$ Then the fork of and is given by^[17]

${displaystyle c,(<),d~mathrel {:=} ~c;a^{textsf {T}}cap d;b^{textsf {T}}.}$

Another form of composition of relations, which applies to general -place relations for is the join operation of relational algebra. The usual composition of two binary relations as defined here can be obtained by taking their join, leading to a ternary relation, followed by a projection that removes the middle component. For example, in the query language SQL there is the operation Join (SQL).

Notes[edit]

^ Bjarni Jónssen (1984) «Maximal Algebras of Binary Relations», in Contributions to Group Theory, K.I. Appel editor American Mathematical Society ISBN 978-0-8218-5035-0
^ ^a ^b ^c Gunther Schmidt (2011) Relational Mathematics, Encyclopedia of Mathematics and its Applications, vol. 132, Cambridge University Press ISBN 978-0-521-76268-7
^ A. De Morgan (1860) «On the Syllogism: IV and on the Logic of Relations»
^ ^a ^b Daniel D. Merrill (1990) Augustus De Morgan and the Logic of Relations, page 121, Kluwer Academic ISBN 9789400920477
^ ^a ^b ^c Gunther Schmidt & Thomas Ströhlein (1993) Relations and Graphs, Springer books
^ Ernst Schroder (1895) Algebra und Logik der Relative
^ Paul Taylor (1999). Practical Foundations of Mathematics. Cambridge University Press. p. 24. ISBN 978-0-521-63107-5. A free HTML version of the book is available at http://www.cs.man.ac.uk/~pt/Practical_Foundations/
^ Michael Barr & Charles Wells (1998) Category Theory for Computer Scientists Archived 2016-03-04 at the Wayback Machine, page 6, from McGill University
^ Rick Nouwen and others (2016) Dynamic Semantics §2.2, from Stanford Encyclopedia of Philosophy
^ John M. Howie (1995) Fundamentals of Semigroup Theory, page 16, LMS Monograph #12, Clarendon Press ISBN 0-19-851194-9
^ Kilp, Knauer & Mikhalev, p. 7
^ ISO/IEC 13568:2002(E), p. 23
^ Unicode character: Z Notation relational composition from FileFormat.info
^ Irving Copilowish (December 1948) «Matrix development of the calculus of relations», Journal of Symbolic Logic 13(4): 193–203 Jstor link, quote from page 203
^ Vaughn Pratt The Origins of the Calculus of Relations, from Stanford University
^ De Morgan indicated contraries by lower case, conversion as M⁻¹, and inclusion with )), so his notation was ${displaystyle nM^{-1})) l.}$
^ Gunther Schmidt and Michael Winter (2018): Relational Topology, page 26, Lecture Notes in Mathematics vol. 2208, Springer books, ISBN 978-3-319-74451-3

References[edit]

M. Kilp, U. Knauer, A.V. Mikhalev (2000) Monoids, Acts and Categories with Applications to Wreath Products and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter,ISBN 3-11-015248-7.

Источник

Определение. Композицией (суперпозицией) двух отношений ρ и σ называется отношение

σ∘ρ = {<x, z> |существует такое y, что <x, y> | ρ и < y, z> |σ}.

Пример 1.

ρ = {<x, y> |y = sinx}.

σ = {<x, y> |y = √x}.

σ∘ρ = {<x, z> |существует такое y, что <x, y> | ρ и < y, z> |σ} = {<x, z> |существует такое y, что y = sinx и z = √y} = {<x, z> | z = √sinx}.

Определение композиции двух отношений соответствует определению сложной функции:

y = f(x), z = g(y) ⟹ z = g(f(x)).

Пример 2.

ρ = {<1, 1>, <1, 2>, <1, 3>, <3, 1>}.

σ = {<1, 2>, <1, 3>, <2, 2>, <3, 2>, <3, 3>}.

Процесс нахождения σ∘ρ в соответствии с определением композиции удобно изобразить таблицей, в которой реализуется перебор всех возможных значений x, y, z. для каждой пары <x, y> | ρ нужно рассмотреть все возможные пары < y, z> |σ (табл. 1).

Таблица 1

<x, y> | ρ

< y, z> |σ

<x, z> |σ∘ρ

<1, 1>

<1, 2>

<1, 3>

<3, 1>

<1, 2>

<1, 3>

<2, 2>

<3, 2>

<3, 3>

<1, 2>

<1, 3>

<1, 2>

<1, 3>

<1, 2>

<1, 3>

<3, 2>

<3, 3>

Заметим, что первая, третья и четвертая, а также вторая и пятая строки последнего столбца таблицы содержат одинаковые пары. Поэтому получим:

σ∘ρ = {<1, 2>, <1, 3>, <3, 2>, <3, 3>}.

Источник

Операции над соответствиями на множествах

Композиция бинарного отношения на множестве

Свойства композиции соответствий

Обратное соответствие и его свойства

Ограничение соответствия

Бинарные отношения.

Композиция отношений.

Теорема о свойствах бинарного отношения.

Definition[edit]

Notational variations[edit]

Properties[edit]

Composition in terms of matrices[edit]

Heterogeneous relations[edit]

Example[edit]

Schröder rules[edit]

Quotients[edit]

Join: another form of composition[edit]

See also[edit]

Notes[edit]

References[edit]

Не пропустите также: