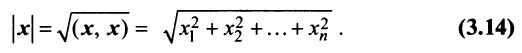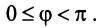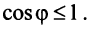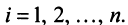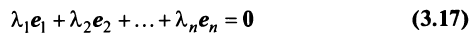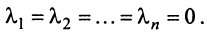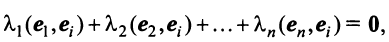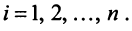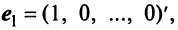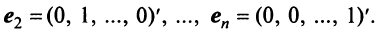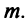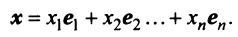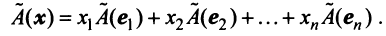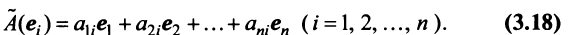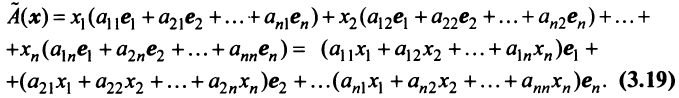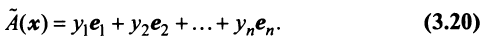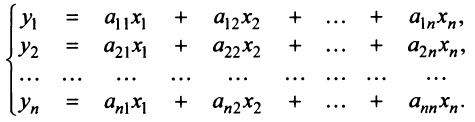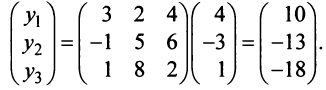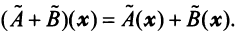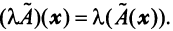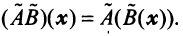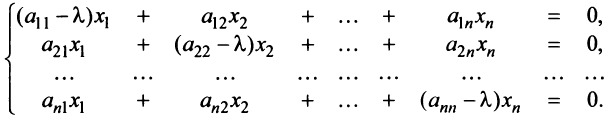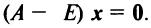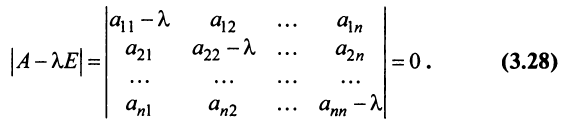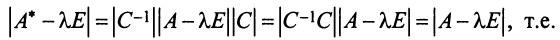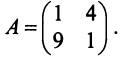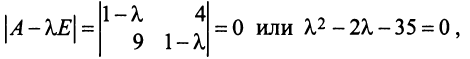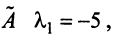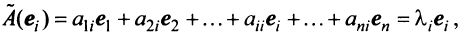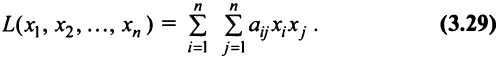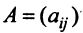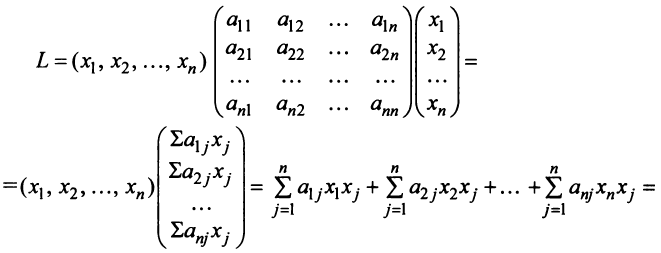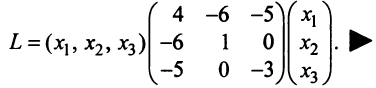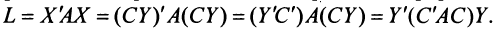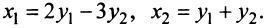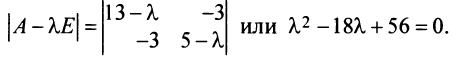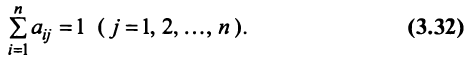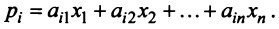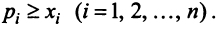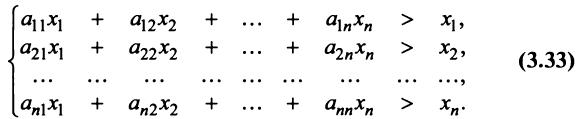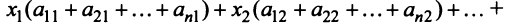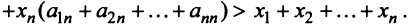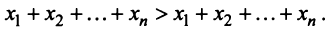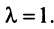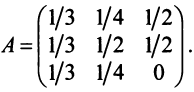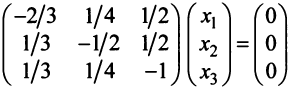Координаты и компоненты вектора
По этой ссылке вы найдёте полный курс лекций по математике:
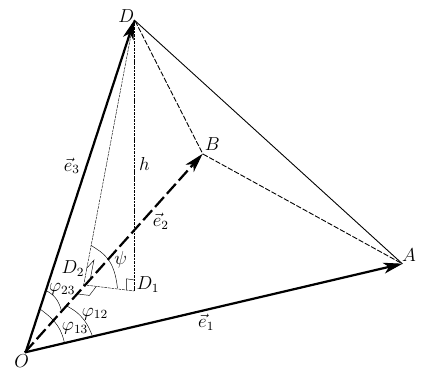
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ох. Оу, Oz (рис. 19). Рассмотрим произвольный вектор а, начало которого лежит в начале координат О, а коней — в точке А. Проведем через точку А плоскости, перпендикулярные .осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Ру Q и R соответственно.
Из рис. 20 видно, что Векторы OP, OQ и OR коллинеарны соответственно единичным векторам i, j, k. поэтому найдутся числа х, у, 2 такие, что и, следовательно, Координаты и компоненты вектора Формула (2) называется разложением вектора и по век/порам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k. Векторы i, j, k попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. с. коэффициенты!, у, z в разложении вектора а по векторам i, j, к определены однозначно.
Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки Л — конца вектора а. Мы пишем в этом случае Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы х, t/j, zk, сумма которых равна вектору а, называются компонентами вектора а.
Возможно вам будут полезны данные страницы:
Из вышеизложенного следует, что два вектора а = {x,y,z} и Ь = {х2,у2,22} равны тогда и только тогда, когда соответственно равны их координаты, т. с. Пусть а = {яь yt, zj}, b = {яг, угУ zi} — коллинеарные векторы, причем b Ф 0. Тогда л = цЬ, т.е. Координаты и компоненты вектора Обратно, если выполняются соотношения (3), то п = цЬ, т. е. векторы а и b коллинеарны.
а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны. Пример. Найти координаты вектора MMi, начало которого находится в точке М(х, у, z). а конец — в точке Afi(«2> 22). Из рис. 22 видно, что ММг = Г2 — п, где р,, р2 — радиус-векторы точек М| и Мг соответственно. Поэтому — координаты вектора ММг равны разностям одноименных координат конечной М^ и начальной М точек этого вектора.
Л 1-4. Произведение
векторов
1. Разложение вектора на компоненты.
Р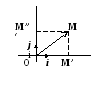
вектор
,
заданный своими координатами:
.
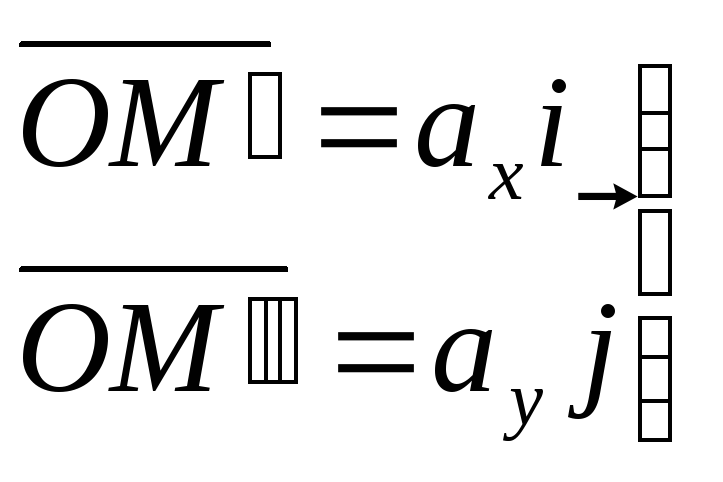
компоненты вектора
по направлениям базисных векторов
.
Выражение вида
называется разложением вектора
на компоненты.
Аналогичным образом можно разложить
на компоненты вектор
:
.
Косинусы углов, образованные рассматриваемым
вектором
с базисными ортами
называются направляющими косинусами
;
;
.
.
2. Скалярное произведение векторов.
Скалярным произведением двух векторов
и
называется число, равное произведению
модулей этих векторов на косинус угла
между ними
Скалярное произведение двух векторов
можно рассматривать как произведение
модуля одного из этих векторов на
ортогональную проекцию другого вектора
на направление первого
.
Свойства:
-
;
-
;
-
;
-
— скалярный квадрат вектора; -
если
Если известны координаты векторов
и
,
то, выполнив разложение векторов на
компоненты
и
,
найдём
,
т.к.
,
,
то
.
.
Условие перпендикулярности векторов:
.
Условие коллинеарности ректоров:
.
3. Векторное произведение векторов.
Векторным произведением вектором
на вектор
называется такой вектор
,
который удовлетворяет условиям:
-
;
-
вектор
перпендикулярен плоскости векторов
и
,
т.е.
,
;
-
вектор
направлен так, что если смотреть с конца
вектора
,
то кратчайший поворот вектора
к вектору
должен происходить против часовой
стрелки.
Свойства:
-
— действие векторного произведения
анти коммутативно; -
— ассоциативно относительно на число; -
— дистрибутивно относительно сложения
векторов; -
Если векторы
и
коллинеарны, то
,
в частности
.
Рассмотренные алгебраические свойства
позволяют найти аналитическое выражение
для векторного произведения через
координаты составляющих векторов в
ортонормированном базисе.
Дано:
и
.
т.к.
,
,
,
,
,
,
,
то
.
Эту формулу можно записать короче, в
форме определителя третьего порядка:
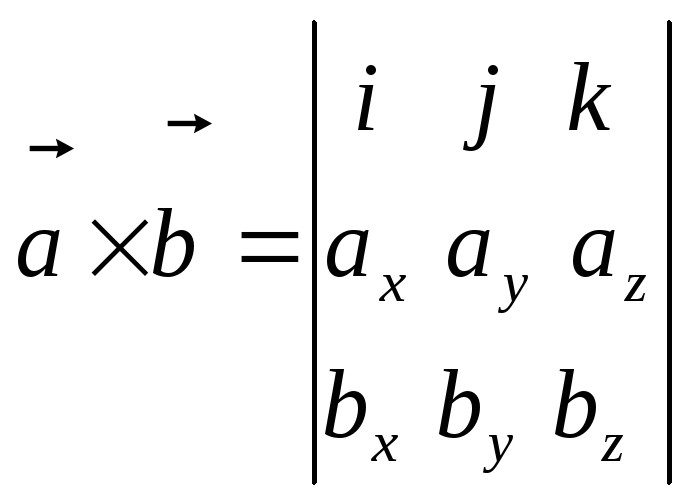
4. Смешанное произведение векторов.
Смешанным произведением трех векторов
,
и
называется число, равное векторному
произведению
,
умноженному скалярно на вектор
.
Верно следующее равенство:
,
поэтому смешанное произведение записывают
.
Как следует из определения, результатом
смешанного произведения трёх векторов
является число. Это число имеет наглядный
геометрический смысл:
Модуль смешанного произведения
равен объёму параллелепипеда, построенного
на приведённых к общему началу векторах
,
и
.
Свойства смешанного произведения:
-
,
т. е. смешанное произведение не меняется
при циклической перестановке векторов; -
т. е. смешанное произведение не меняется
при перестановке знаков векторного и
скалярного произведения; -
,
т.е. смешанное произведение меняет знак
на противоположный при перестановки
двух векторов – сомножителей; -
(объём параллелепипеда равен нулю),
если векторы
,
,
лежат в одной или параллельных плоскостях,
следовательно они компланарны или два
из перемножаемых векторов коллинеарны. -
;
-
;
-
.
Если векторы
,
,
заданы в ортонормированном базисе
своими координатами, вычисление
смешанного произведения осуществляется
по формуле
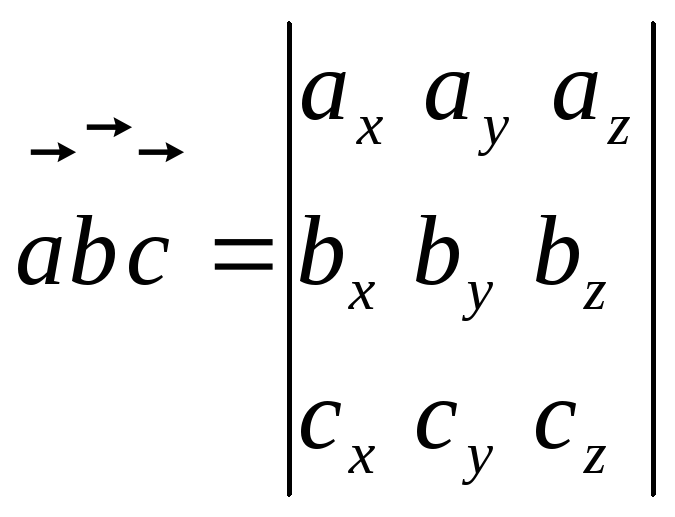
Действительно, если
,
то
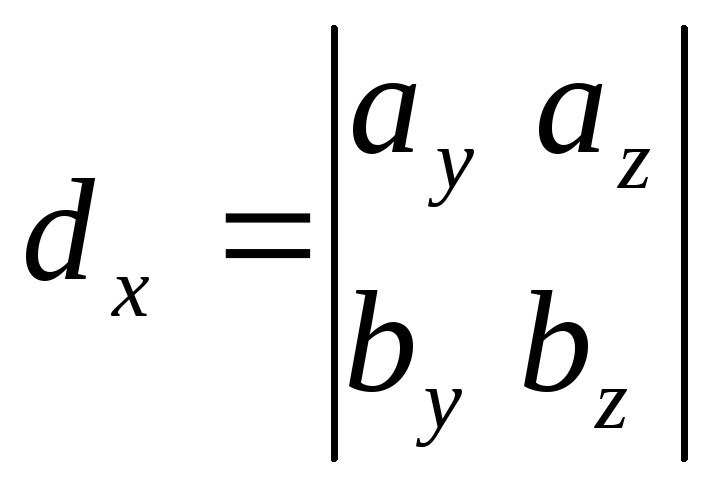
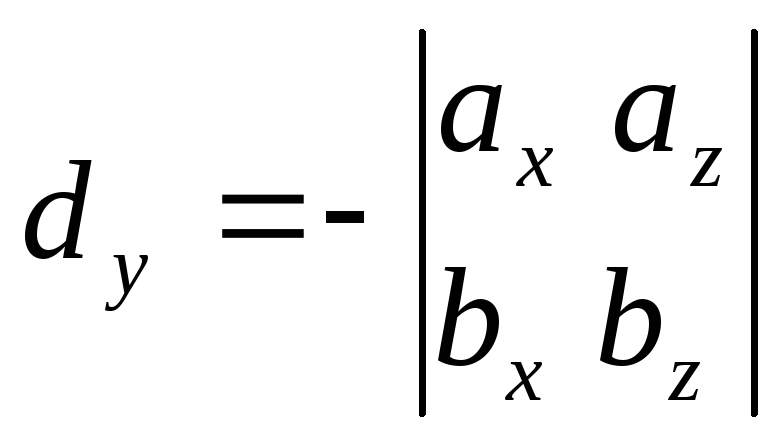
,
тогда
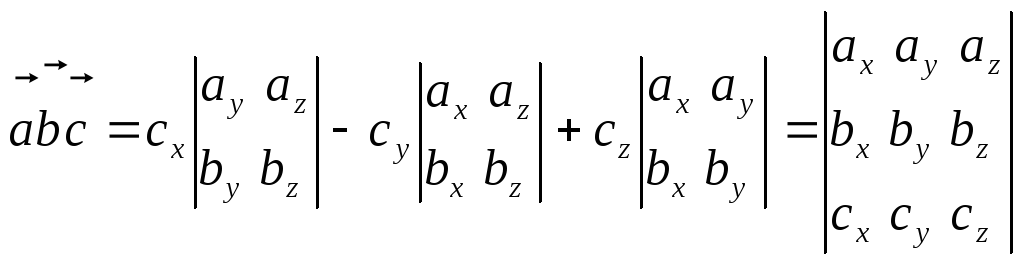
Если векторы
,
,
компланарны, то векторное произведение
перпендикулярно вектору
.
И наоборот, если
,
то объем параллелепипеда равен нулю, а
это возможно только в том случае, когда
векторы компланарны (линейно зависимы).
Таким образом, три вектора компланарны,
тогда и только тогда, когда их смешанное
произведение равно нулю.
Соседние файлы в папке модуль1
- #
- #
02.06.2015205.82 Кб27Л3.doc
- #
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 — 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Как найти базис системы векторов примеры. Как найти базис данной системы векторов
Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
или в развернутом виде .
Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке. Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов .
.
Разрешенная система векторов, равносильная исходной, имеет вид
Векторы а 1 1 , а 3 1 , а 4 1 образуют диагональную систему. Следовательно, векторы а 1 , а 3 , а 4 образуют базис системы векторов а 1 , а 2 , а 3 , а 4 , а 5 .
Разложим теперь векторы а 2 и а 5 по базису а 1 , а 3 , а 4 . Для этого сначала разложим соответствующие векторы а 2 1 и а 5 1 по диагональной системе а 1 1 , а 3 1 , а 4 1 , имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты x i .
Векторы а 2 и а 5 разлагаются по базису а 1 , а 3 , а 4 с теми же коэффициентами, что и векторы а 2 1 и а 5 1 по диагональной системе а 1 1 , а 3 1 , а 4 1 (те коэффициенты x i ). Следовательно,
Задания. 1 .Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
2. Найти все базисы системы векторов:
В геометрии вектор понимается как направленный отрезок, причем векторы, полученные один из другого параллельным переносом, считаются равными. Все равные векторы рассматриваются как один и тот же вектор. Начало вектора можно поместить в любую точку пространства или плоскости.
Если в пространстве заданы координаты концов вектора : A (x 1 , y 1 , z 1), B (x 2 , y 2 , z 2), то
Аналогичная формула имеет место на плоскости. Это значит, что вектор можно записать в виде координатной строки. Операции над векторами, – сложение и умножение на число, над строками выполняются покомпонентно. Это дает возможность расширить понятие вектора, понимая под вектором любую строку чисел. Например, решение системы линейных уравнений, а также любой набор значений переменных системы, можно рассматривать как вектор.
Над строками одинаковой длины операция сложения выполняется по правилу
(a 1 , a 2 , … , a n ) + (b 1 , b 2 , … , b n ) = (a 1 + b 1 , a 2 + b 2 , … , a n + b n ). (2)
Умножение строки на число выполняется по правилу
l(a 1 , a 2 , … , a n ) = (la 1 , la 2 , … , la n ). (3)
Множество векторов-строк заданной длины n с указанными операциями сложения векторов и умножения на число образует алгебраическую структуру, которая называется n-мерным линейным пространством .
Линейной комбинацией векторов называется вектор , где λ 1 , . , λ m – произвольные коэффициенты.
Система векторов называется линейно зависимой, если существует ее линейная комбинация, равная , в которой есть хотя бы один ненулевой коэффициент.
Система векторов называется линейно независимой, если в любой ее линейной комбинации, равной , все коэффициенты нулевые.
Таким образом, решение вопроса о линейной зависимости системы векторов сводится к решению уравнения
Если у этого уравнения есть ненулевые решения, то система векторов линейно зависима. Если же нулевое решение является единственным, то система векторов линейно независима.
Для решения системы (4) можно для наглядности векторы записать не в виде строк, а в виде столбцов.
Тогда, выполнив преобразования в левой части, придем к системе линейных уравнений, равносильной уравнению (4). Основная матрица этой системы образована координатами исходных векторов, расположенных по столбцам. Столбец свободных членов здесь не нужен, так как система однородная.
Базисом системы векторов (конечной или бесконечной, в частности, всего линейного пространства) называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.
Пример 1.5.2. Найти базис системы векторов = (1, 2, 2, 4), = (2, 3, 5, 1), = (3, 4, 8, –2), = (2, 5, 0, 3) и выразить остальные векторы через базис.
Решение . Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Это матрица системы x 1 + x 2 + x 3 + x 4 =. . Приводим матрицу к ступенчатому виду:
Базис данной системы векторов образуют векторы , , , которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора решаем уравнение x 1 + x 2 + x 4 = . Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего , на место столбца свободных членов. Поэтому при приведении к ступенчатому виду над матрицей будут сделаны те же преобразования, что выше. Значит, можно использовать полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки столбцов: столбцы с кружками помещаем слева от вертикальной черты, а столбец, соответствующий вектору , помещаем справа от черты.
Замечание . Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. При этом каждая система решается независимо от остальных.
У п р а ж н е н и е 1.4. Найти базис системы векторов и выразить остальные векторы через базис:
а) = (1, 3, 2, 0), = (3, 4, 2, 1), = (1, –2, –2, 1), = (3, 5, 1, 2);
б) = (2, 1, 2, 3), = (1, 2, 2, 3), = (3, –1, 2, 2), = (4, –2, 2, 2);
в) = (1, 2, 3), = (2, 4, 3), = (3, 6, 6), = (4, –2, 1); = (2, –6, –2).
В заданной системе векторов базис обычно можно выделить разными способами, но во всех базисах будет одинаковое число векторов. Число векторов в базисе линейного пространства называется размерностью пространства. Для n -мерного линейного пространства n – это размерность пространства, так как это пространство имеет стандартный базис = (1, 0, … , 0), = (0, 1, … , 0), … , = (0, 0, … , 1). Через этот базис любой вектор = (a 1 , a 2 , … , a n ) выражается следующим образом:
= (a 1 , 0, … , 0) + (0, a 2 , … , 0) + … + (0, 0, … , a n ) =
A 1 (1, 0, … , 0) + a 2 (0, 1, … , 0) + … + a n (0, 0, … ,1) = a 1 + a 2 +… + a n .
Таким образом, компоненты в строке вектора = (a 1 , a 2 , … , a n ) – это его коэффициенты в разложении через стандартный базис.
Прямые на плоскости
Задача аналитической геометрии – применение к геометрическим задачам координатного метода. Тем самым задача переводится в алгебраическую форму и решается средствами алгебры.
Когда мы разбирали понятия n -мерного вектора и вводили операции над векторами, то выяснили, что множество всех n -мерных векторов порождает линейное пространство. В этой статье мы поговорим о важнейших связанных понятиях – о размерности и базисе векторного пространства. Также рассмотрим теорему о разложении произвольного вектора по базису и связь между различными базисами n -мерного пространства. Подробно разберем решения характерных примеров.
Навигация по странице.
Понятие размерности векторного пространства и базиса.
Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.
Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
Приведем некоторые рассуждения, основываясь на этих определениях.
Рассмотрим пространство n -мерных векторов.
Покажем, что размерность этого пространства равна n .
Возьмем систему из n единичных векторов вида
Примем эти векторы в качестве строк матрицы А . В этом случае матрица А будет единичной матрицей размерности n на n . Ранг этой матрицы равен n (при необходимости смотрите статью ). Следовательно, система векторов линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы являются базисом этого пространства .
Из последнего утверждения и определения базиса можно сделать вывод, что любая система n -мерных векторов, число векторов в которой меньше n , не является базисом .
Теперь переставим местами первый и второй вектор системы . Легко показать, что полученная система векторов также является базисом n -мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n . Таким образом, система из n векторов линейно независима и является базисом n -мерного векторного пространства.
Если переставить местами другие векторы системы , то получим еще один базис.
Если взять линейно независимую систему не единичных векторов, то она также является базисом n -мерного векторного пространства.
Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n -мерных векторов.
Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.
Рассмотрим несколько примеров.
Являются ли векторы базисом трехмерного векторного пространства?
Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:
Таким образом, векторы a , b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.
Может ли система векторов быть базисом векторного пространства?
Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема исходной системы векторов является базисом).
Убедитесь, что векторы
могут быть базисом четырехмерного векторного пространства.
Составим матрицу, приняв ее строками исходные векторы:
Найдем :
Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.
Исходные векторы действительно являются базисом четырехмерного пространства.
Составляют ли векторы базис векторного пространства размерности 4 ?
Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).
Нет, не составляет.
Разложение вектора по базису векторного пространства.
Пусть произвольные векторы являются базисом n -мерного векторного пространства. Если к ним добавить некоторый n -мерный вектор x , то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.
Так мы подошли к очень важной теореме.
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Пусть — базис n -мерного векторного пространства. Добавим к этим векторам n -мерный вектор x . Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где — некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.
Предположим, что существует еще одно разложение , где — некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :
Так как система базисных векторов линейно независима, то по определению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.
Коэффициенты называются координатами вектора x в базисе .
После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n -мерный вектор ». Это выражение означает, что мы рассматриваем вектор x n -мерного векторного пространства, координаты которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .
Рассмотрим следующую задачу.
Пусть в некотором базисе n -мерного векторного пространства нам задана система из n линейно независимых векторов
и вектор . Тогда векторы также являются базисом этого векторного пространства.
Пусть нам требуется найти координаты вектора x в базисе . Обозначим эти координаты как .
Вектор x в базисе имеет представление . Запишем это равенство в координатной форме:
Это равенство равносильно системе из n линейных алгебраических уравнений с n неизвестными переменными :
Основная матрица этой системы имеет вид
Обозначим ее буквой А . Столбцы матрицы А представляют собой векторы линейно независимой системы векторов , поэтому ранг этой матрицы равен n , следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, или .
Так будут найдены искомые координаты вектора x в базисе .
Разберем теорию на примерах.
В некотором базисе трехмерного векторного пространства заданы векторы
Убедитесь, что система векторов также является базисом этого пространства и найдите координаты вектора x в этом базисе.
Чтобы система векторов была базисом трехмерного векторного пространства нужно, чтобы она была линейно независима. Выясним это, определив ранг матрицы A , строками которой являются векторы . Ранг найдем методом Гаусса
следовательно, Rank(A) = 3 , что показывает линейную независимость системы векторов .
Итак, векторы являются базисом. Пусть в этом базисе вектор x имеет координаты . Тогда, как мы показали выше, связь координат этого вектора задается системой уравнений
Подставив в нее известные из условия значения, получим
Решим ее методом Крамера:
Таким образом, вектор x в базисе имеет координаты .
В некотором базисе четырехмерного векторного пространства задана линейно независимая система векторов
Известно, что . Найдите координаты вектора x в базисе .
Так как система векторов линейно независима по условию, то она является базисом четырехмерного пространства. Тогда равенство означает, что вектор x в базисе имеет координаты . Обозначим координаты вектора x в базисе как .
Система уравнений, задающая связь координат вектора x в базисах и имеет вид
Подставляем в нее известные значения и находим искомые координаты :
.
Связь между базисами.
Пусть в некотором базисе n -мерного векторного пространства заданы две линейно независимые системы векторов
и
то есть, они тоже являются базисами этого пространства.
Если — координаты вектора в базисе , то связь координат и задается системой линейных уравнений (об этом мы говорили в предыдущем пункте):
, которая в матричной форме может быть записана как
Аналогично для вектора мы можем записать
Предыдущие матричные равенства можно объединить в одно, которое по сути задает связь векторов двух различных базисов
Аналогично мы можем выразить все векторы базиса через базис :
Матрицу называют матрицей перехода от базиса к базису , тогда справедливо равенство
Умножив обе части этого равенства справа на
получим
Найдем матрицу перехода, при этом не будем подробно останавливаться на нахождении обратной матрицы и умножении матриц (смотрите при необходимости статьи и ):
Осталось выяснить связь координат вектора x в заданных базисах.
Пусть в базисе вектор x имеет координаты , тогда
а в базисе вектор x имеет координаты , тогда
Так как левые части последних двух равенств одинаковы, то мы можем приравнять правые части:
Если умножить обе части справа на
С другой стороны
(найдите обратную матрицу самостоятельно).
Два последних равенства дают нам искомую связь координат вектора x в базисах и .
Матрица перехода от базиса к базису имеет вид
;
координаты вектора x в базисах и связаны соотношениями
или
.
Мы рассмотрели понятия размерности и базиса векторного пространства, научились раскладывать вектор по базису и обнаружили связь между разными базисами n-мерного пространства векторов через матрицу перехода.
Лекции по алгебре и геометрии. Семестр 1.
Лекция 9. Базис векторного пространства.
Краткое содержание: система векторов, линейная комбинация системы векторов, коэффициенты линейной комбинации системы векторов, базис на прямой, плоскости и в пространстве, размерности векторных пространств на прямой, плоскости и в пространстве, разложение вектора по базису, координаты вектора относительно базиса, теорема о равенстве двух векторов, линейные операции с векторами в координатной форме записи, ортонормированная тройка векторов, правая и левая тройки векторов, ортонормированный базис, основная теорема векторной алгебры.
Глава 9. Базис векторного пространства и разложение вектора по базису.
п.1. Базис на прямой, на плоскости и в пространстве.
Определение. Любое конечное множество векторов называется системой векторов.
Определение. Выражение , где
называется линейной комбинацией системы векторов
, а числа
называются коэффициентами этой линейной комбинации.
Пусть L, Р и S – прямая, плоскость и пространство точек соответственно и
. Тогда
– векторные пространства векторов как направленных отрезков на прямой L, на плоскости Р и в пространстве S соответственно.
называется любой ненулевой вектор
, т.е. любой ненулевой вектор коллинеарный прямой L:
и
.
Обозначение базиса
:
– базис
.
Определение. Базисом векторного пространства
называется любая упорядоченная пара неколлинеарных векторов пространства
.
, где
,
– базис
.
Определение. Базисом векторного пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
.
– базис
.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве
по определению, в пространстве
два вектора будут коллинеарные, если хотя бы один из них нулевой, в пространстве
три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
п.2. Разложение вектора по базису.
Определение. Пусть – произвольный вектор,
– произвольная система векторов. Если выполняется равенство
то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов
является базисом векторного пространства, то равенство (1) называется разложением вектора по базису
. Коэффициенты линейной комбинации
называются в этом случае координатами вектора относительно базиса
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и
– базис
. Возьмем произвольный вектор
. Так как оба вектора и коллинеарные одной и той же прямой L, то
. Воспользуемся теоремой о коллинеарности двух векторов. Так как
, то найдется (существует) такое число
, что
и тем самым мы получили разложение вектора по базису
векторного пространства
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису
векторного пространства
:
и
, где
. Тогда
и используя закон дистрибутивности, получаем:
Так как
, то из последнего равенства следует, что
, ч.т.д.
2) Пусть теперь Р произвольная плоскость и
– базис
. Пусть
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую
, на которой лежит вектор . Через конец вектора проведем прямую параллельную вектору и прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма
, и
,
,
– базис ,
– базис
.
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа
, что
и
. Отсюда получаем:
и возможность разложения по базису доказана.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора по базису
векторного пространства
:
и
. Получаем равенство
Откуда следует
. Если
, то
, а т.к.
, то
и коэффициенты разложения равны:
,
. Пусть теперь
. Тогда
, где
. По теореме о коллинеарности двух векторов отсюда следует, что
. Получили противоречие условию теоремы. Следовательно,
и
, ч.т.д.
3) Пусть
– базис
и пусть
произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора
и вектор от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
, плоскость
и плоскость
; далее через конец вектора проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
По правилу сложения векторов получаем равенство:
. (1)
По построению
. Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число
, такое что
. Аналогично,
и
, где
. Теперь, подставляя эти равенства в (1), получаем:
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису
:
Заметим, что по условию векторы
некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая:
или
.
а) Пусть
, тогда из равенства (3) следует:
. (4)
Из равенства (4) следует, что вектор раскладывается по базису
, т.е. вектор лежит в плоскости векторов
и, следовательно, векторы
компланарные, что противоречит условию.
б) Остается случай
, т.е.
. Тогда из равенства (3) получаем или
Так как
– базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что
и
, ч.т.д.
1) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и множеством действительных чисел R.
2) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и декартовым квадратом
3) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и декартовым кубом
множества действительных чисел R.
Доказательство. Докажем третье утверждение. Первые два доказываются аналогично.
Выберем и зафиксируем в пространстве
какой-нибудь базис
и устроим отображение
по следующему правилу:
т.е. каждому вектору поставим в соответствие упорядоченный набор его координат.
Так как при фиксированном базисе каждый вектор имеет единственный набор координат, то соответствие, задаваемое правилом (6) действительно является отображением.
Из доказательства теоремы следует, что различные векторы имеют различные координаты относительно одного и того же базиса, т.е. отображение (6) является инъекцией.
Пусть
произвольный упорядоченный набор действительных чисел.
Рассмотрим вектор
. Этот вектор по построению имеет координаты
. Следовательно, отображение (6) является сюръекцией.
Отображение, которое одновременно инъективное и сюръективное является биективным, т.е. взаимно однозначным, ч.т.д.
Теорема. (О равенстве двух векторов.)
Два вектора равны тогда и только тогда, когда равны их координаты относительно одного и того же базиса.
Доказательство сразу же вытекает из предыдущего следствия.
п.3. Размерность векторного пространства.
Определение. Число векторов в базисе векторного пространства называется его размерностью.
Обозначение:
– размерность векторного пространства V.
Таким образом, в соответствие с этим и предыдущими определениями, имеем:
1)
– векторное пространство векторов прямой L.
– базис
,
,
,
– разложение вектора
по базису
,
– координата вектора относительно базиса
.
2)
– векторное пространство векторов плоскости Р.
– базис
,
,
,
– разложение вектора
по базису
,
– координаты вектора относительно базиса
.
3)
– векторное пространство векторов в пространстве точек S.
– базис
,
,
– разложение вектора
по базису
,
– координаты вектора относительно базиса
.
Замечание. Если
, то
и можно выбрать базис
пространства
так, что
– базис
и
– базис
. Тогда
, и
, .
Таким образом, любой вектор прямой L, плоскости Р и пространства S можно разложить по базису
:
Обозначение. В силу теоремы о равенстве векторов, мы можем отождествить любой вектор с упорядоченной тройкой действительных чисел и писать:
Это возможно лишь том случае, когда базис
фиксирован и нет опасности спутаться.
Определение. Запись вектора в виде упорядоченной тройки действительных чисел называют координатной формой записи вектора:
.
п.4. Линейные операции с векторами в координатной форме записи.
Пусть
– базис пространства
и
– два его произвольных вектора. Пусть
и
– запись этих векторов в координатной форме. Пусть, далее,
– произвольное действительное число. В этих обозначениях имеет место следующая теорема.
Теорема. (О линейных операциях с векторами в координатной форме.)
2)
.
Другими словами, для того, чтобы сложить два вектора нужно сложить их соответствующие координаты, а чтобы умножить вектор на число, нужно каждую координату данного вектора умножить на данное число.
Доказательство. Так как по условию теоремы , , то используя аксиомы векторного пространства, которым подчиняются операции сложения векторов и умножения вектора на число, получаем:
Аналогично доказывается второе равенство.
п.5. Ортогональные векторы. Ортонормированный базис.
Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е.
.
Обозначение:
– векторы и ортогональны.
Определение. Тройка векторов
называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е.
,
.
Определение. Тройка векторов
называется ортонормированной, если она ортогональная и длины всех векторов равны единице:
.
Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.
Определение. Упорядоченная некомпланарная тройка векторов
, отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора на плоскость, в которой лежат первые два вектора и , кратчайший поворот первого вектора ко второму происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).
Здесь, на рис.6 изображена правая тройка векторов
. На следующем рис.7 изображена левая тройка векторов
:
Определение. Базис
векторного пространства
называется ортонормированным, если
ортонормированная тройка векторов.
Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом
, см. следующий рисунок.
Выражение вида называется линейной комбинацией векторов A 1 , A 2 . A n с коэффициентами λ 1, λ 2 . λ n .
Определение линейной зависимости системы векторов
Система векторов A 1 , A 2 . A n называется линейно зависимой , если существует ненулевой набор чисел λ 1, λ 2 . λ n , при котором линейная комбинация векторов λ 1 *A 1 +λ 2 *A 2 +. +λ n *A n равна нулевому вектору , то есть система уравнений: имеет ненулевое решение.
Набор чисел λ 1, λ 2 . λ n является ненулевым, если хотя бы одно из чисел λ 1, λ 2 . λ n отлично от нуля.
Определение линейной независимости системы векторов
Система векторов A 1 , A 2 . A n называется линейно независимой , если линейная комбинация этих векторов λ 1 *A 1 +λ 2 *A 2 +. +λ n *A n равна нулевому вектору только при нулевом наборе чисел λ 1, λ 2 . λ n , то есть система уравнений: A 1 x 1 +A 2 x 2 +. +A n x n =Θ имеет единственное нулевое решение.
Проверить, является ли линейно зависимой система векторов
1. Составляем систему уравнений :
2. Решаем ее методом Гаусса . Преобразования Жордано системы приведены в таблице 29.1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.
3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:
5. Задав по своему усмотрению значение свободной переменной x 3 =1, получаем частное ненулевое решение X=(-3,2,1).
Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A 1 +2A 2 +1A 3 =Θ. Следовательно, система векторов линейно зависимая .
Свойства систем векторов
Свойство (1)
Если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.
Свойство (2)
Если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.
Свойство (3)
Если система векторов линейно независимая, то любая ее подсистема линейно независимая.
Свойство (4)
Любая система векторов, содержащая нулевой вектор, линейно зависимая.
Свойство (5)
Система m-мерных векторов всегда является линейно зависимой, если число векторов n больше их размерности (n>m)
Базис системы векторов
Базисом системы векторов A 1 , A 2 . A n называется такая подсистема B 1 , B 2 . B r (каждый из векторов B 1 ,B 2 . B r является одним из векторов A 1 , A 2 . A n) , которая удовлетворяет следующим условиям:
1. B 1 ,B 2 . B r линейно независимая система векторов;
2. любой вектор A j системы A 1 , A 2 . A n линейно выражается через векторы B 1 ,B 2 . B r
r — число векторов входящих в базис.
Теорема 29.1 О единичном базисе системы векторов.
Если система m-мерных векторов содержит m различных единичных векторов E 1 E 2 . E m , то они образуют базис системы.
Алгоритм нахождения базиса системы векторов
Для того, чтобы найти базис системы векторов A 1 ,A 2 . A n необходимо:
- Составить соответствующую системе векторов однородную систему уравнений A 1 x 1 +A 2 x 2 +. +A n x n =Θ
- Привести эту систему
Популярное
- Бизнес идеи — промышленный альпинизм как бизнес Человеку, который имеет свой плей л.
Совместимость стрельца и весов Человеку, который имеет свой плей л.
Как легко избавиться от проблем и начать радоваться жизни! Человеку, который имеет свой плей л.
Знаки зодиака по стихиям и их совместимость Все о моем знаке Человеку, который имеет свой плей л.
Выращивание и сбыт вешенки для получения прибыли Человеку, который имеет свой плей л.
Свежие записи
- Вкусные букеты из овощей и фруктов с поздравлениями Человеку, который имеет свой плей л.
Петровская икона Богоматери, некий «700-летний юбилей свт Человеку, который имеет свой плей л.
Как женить на себе мужчину рака Человеку, который имеет свой плей л.
Автоковрики EVA: Как шить? Человеку, который имеет свой плей л.
Медитация на омоложение и усиление привлекательности Правила эффективной медитации Человеку, который имеет свой плей л.
http://bstudy.net/719717/estestvoznanie/algoritm_nahozhdeniya_bazisa_sistemy_vektorov
http://myfd.ru/kak-naiti-bazis-sistemy-vektorov-primery-kak-naiti-bazis/
Содержание:
Векторы на плоскости и в пространстве:
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Вектором называется направленный отрезок
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
Длиной (или модулем) 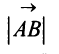
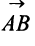
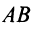
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 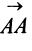
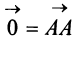
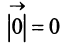
Произведением вектора 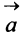
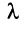
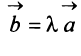
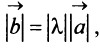
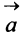
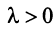
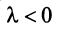
Противоположным вектором 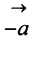
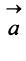
Рис. 32
Суммой двух векторов 

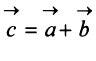




Очевидно, что вектор 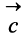


Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 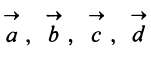
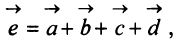

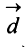
Нетрудно убедиться. что вектор 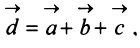


Разностью двух векторов 



Легко убедиться в том, что в параллелограмме, построенном на векторах 
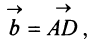


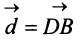
Перенесем вектор 

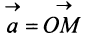
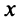
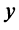
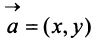
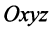
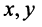
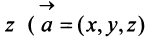
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов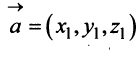
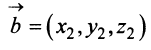
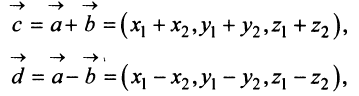
а произведение вектора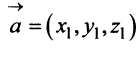
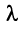
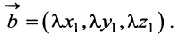
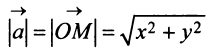
Определение. Скалярным произведением 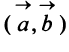


Выразим скалярное произведение через координаты векторов 

Из треугольника 
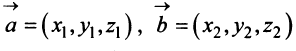
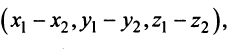
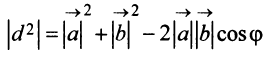
Учитывая формулу длины вектора (3.1) найдем
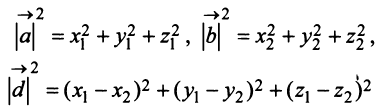
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 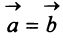
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 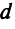
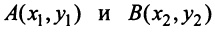
Поэтому
Угол между векторами

Пример:
Даны векторы
Найти: а)векторы 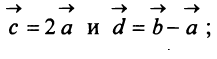
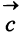
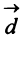
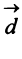
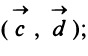
Решение:
а) По определению
б) По формуле (3.1) найдем длины векторов
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.
г) По формуле (3.3) скалярное произведение
д) По формуле (3.6) угол между векторами 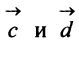
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение.
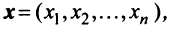
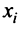
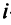
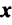
Понятие 
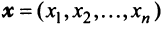
Два 
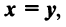
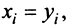
Суммой двух векторов одинаковой размерности п называется вектор 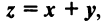
Произведением вектора 
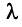
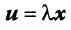
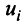
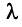

Линейные операции над любыми векторами удовлетворяют следующим свойствам:
— коммутативное (переместительное) свойство суммы:
— ассоциативное (сочетательное) свойство суммы;
— ассоциативное относительно числового множителя свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;
—дистрибутивное относительно суммы числовых множителей свойство;
- Существует нулевой вектор
такой, что
для любого вектора
(особая роль нулевого вектора);
- Для любого вектора
существует противоположный вектор
такой, что
для любого вектора
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под 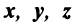
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 



Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора 
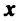
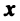
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 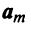

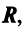
где 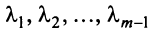
Определение. Векторы 
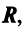
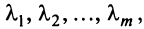
В противном случае векторы 
Из приведенных выше определений следует, что векторы 
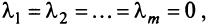
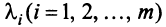
Можно показать (аналогично § 1.6), что если векторы 
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 
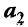
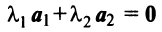
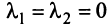
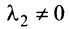
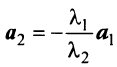
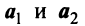
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
то равенство (3.8) справедливо при
- Если часть векторов
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
линейно зависимы, то справедливо равенство
в котором не все числа равны нулю. Но тогда с теми же числами
и
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы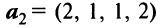
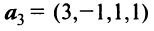
Решение:
Составим векторное равенство 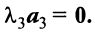
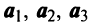
Задача свелась таким образом к решению системы:
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
откуда найдем, бесконечное множество ее решений 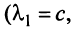
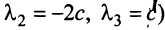
Итак, для ‘данных векторов условие (3.8) выполняется не только при 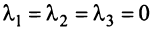
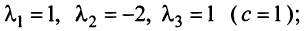
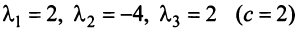
Определение. Линейное пространство 
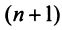


Определение. Совокупность 


Теорема. Каждый вектор 

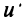

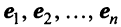




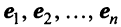

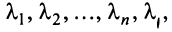
При этом 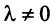
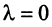
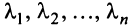
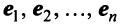
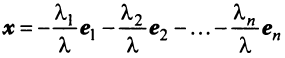
где
Это выражение 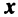

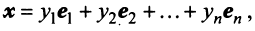
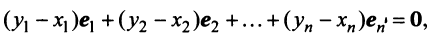

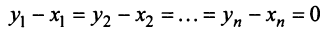
Равенство (3.9) называется разложением вектора 

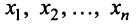

Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если 

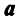




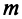

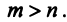

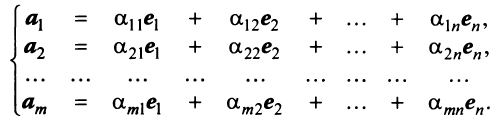
Ранг этой матрицы не превосходит 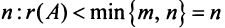
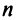
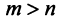
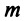
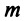
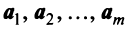


Пример:
В базисе 
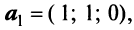
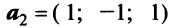
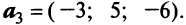
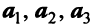
Решение:
Векторы 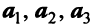
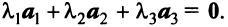
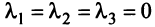
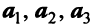
Переход к новому базису
Пусть в пространстве 

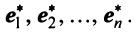
Полученная система означает, что переход от старого базиса 
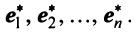
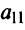
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 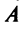
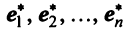
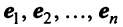
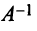
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 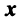
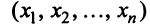
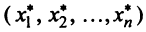
Подставив значения 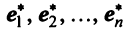
т.е. в матричной форме
Пример:
По условию примера 3.3 вектор 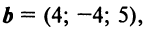
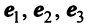
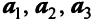
Решение:
Выразим связь между базисами:
Матрица перехода от базиса 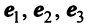
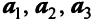
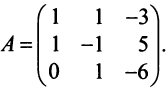
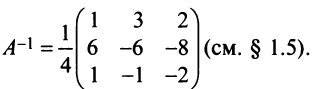
т.е. новые координаты вектора 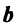
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов 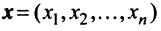
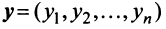
Скалярное произведение имеет экономический смысл. Если 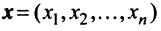
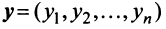
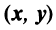
Скалярное произведение имеет следующие свойства:
— коммутативное свойство;
— дистрибутивное свойство;
— для любого действительного числа;
если
— ненулевой вектор;
, если
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 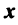
Имеют место следующие свойства длины вектора:
1. 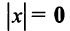
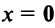
2. 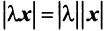
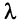
3.
(неравенство Коши—Буняковского);
4. 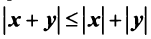
Угол 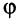

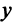

Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 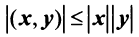
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 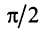
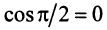
Векторы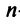
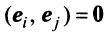
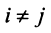
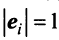
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 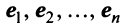
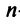

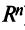
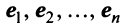
справедливо лишь при
Действительно, умножая скалярно равенство (3.17) на любой вектор 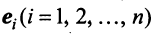
откуда, учитывая, что 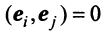
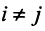
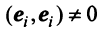
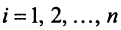
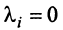
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 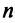
Примером ортонормированного базиса является система 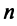
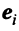
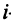
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства: 
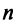

Определение. Если задан закон (правило), по которому каждому вектору 


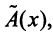


Оператор (преобразование) называется линейным, если для любых векторов 
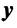

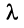
Вектор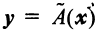


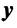
Если пространства 



Выберем в пространстве 

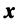
В силу линейности оператора 
Поскольку 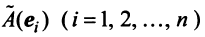


Тогда
С другой стороны, вектор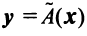

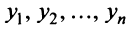
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
Матрица



Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 
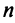
Связь между вектором 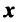
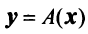
где 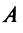

Пример:
Пусть в пространстве 

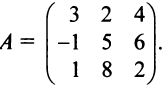
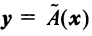
Решение:
По формуле (3.21) имеем
Следовательно, 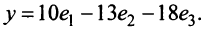
Определим действия над линейными операторами.
Суммой двух линейных операторов 
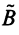
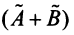
Произведением линейного оператора 
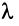
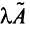
Произведением линейных операторов 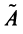
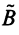
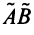
Можно убедиться в том, что операторы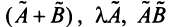
Определим нулевой оператор 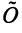
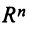
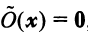
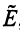
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы 
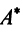

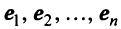
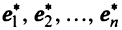
где 



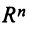
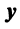
(в новом базисе). Так как 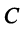
Умножим равенство (3.24) слева на матрицу 
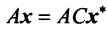
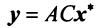
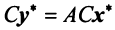
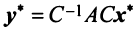
Пример:
В базисе 

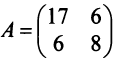

Решение:
Матрица перехода здесь 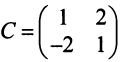
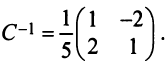
Собственные векторы и собственные значения линейного оператора
Определение. Вектор 

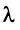
Число 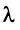


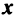
Из определения следует, что собственный вектор под действием линейного оператора 
Равенство (3.26) можно записать в матричной форме:
где вектор 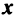
Перепишем систему так, чтобы в правых частях были нули:
или в матричном виде
Полученная однородная система всегда имеет нулевое решение 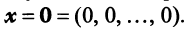
Определитель 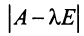




Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 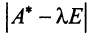
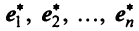
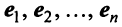
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
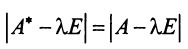
Пример:
Найти собственные значения и собственные векторы линейного оператора 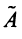
Решение:
Составляем характеристическое уравнение
откуда собственные значения линейного оператора
Находим собственный вектор 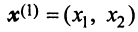
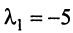
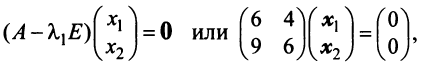
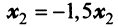
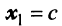
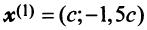
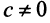

Аналогично можно убедиться в том, что векторы 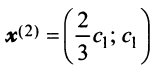
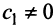

Наиболее простой вид принимает матрица 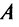

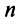
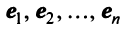
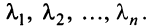
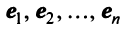
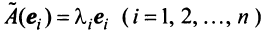
откуда 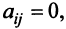
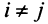
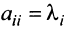

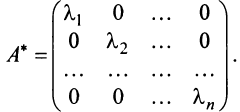


Можно доказать, что если линейный оператор имеет 
- Заказать решение задач по высшей математике
Пример:
Привести матрицу 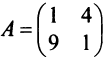

Решение:
В примере 3.7 были найдены собственные значения матрицы 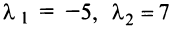
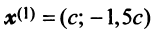
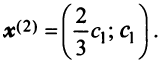
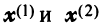
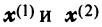
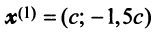
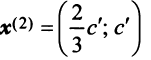
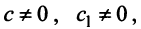
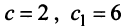
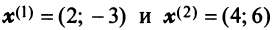
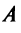
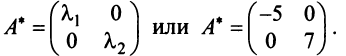
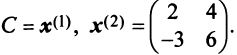
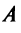
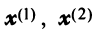
или после вычислений (которые мы опускаем)
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 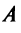
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 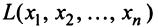
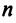
Предполагаем, что коэффициенты квадратичной формы 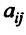
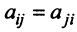
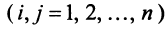
где 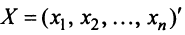
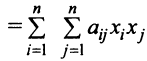
Пример:
Дана квадратичная форма 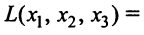
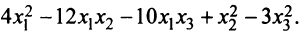
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 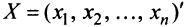
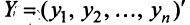
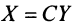
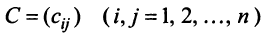
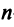
, Итак, при невырожденном линейном преобразовании 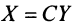
Пример:
Дана квадратичная форма 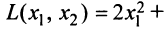
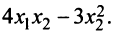
Решение:
Матрица данной квадратичной формы 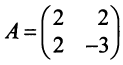
Следовательно, по (3.31) матрица искомой квадратичной формы 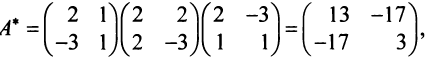
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 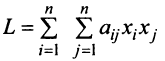
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
Решение:
Вначале вьделим полный квадрат при переменной 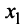
Теперь выделяем полный квадрат при переменной 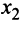
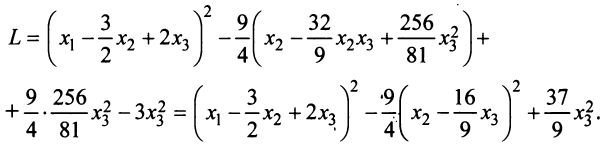
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 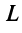
применив невырожденное линейное преобразование
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 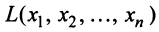
Так, например, квадратичная форма 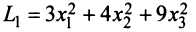
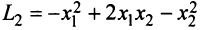
Теорема. Для того чтобы квадратичная форма 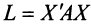
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 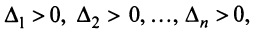

Пример:
Доказать, что квадратичная форма 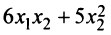
Решение:
Первый способ. Матрица 

Решая уравнение, найдем 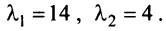

Второй способ. Так как главные миноры матрицы 
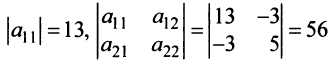
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 
Рассмотрим матрицу
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 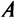
Для любой страны 
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 
Если считать, что 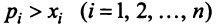
Сложив все неравенства системы (3.33), получим после группировки
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
Таким образом, неравенство 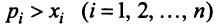
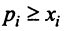
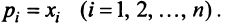
Вводя вектор 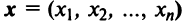
В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы 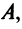
Пример:
Структурная матрица торговли трех стран 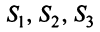
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 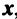
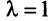
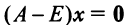
методом Гаусса. Найдем 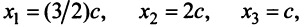
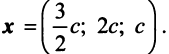
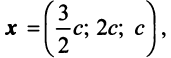
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
Время на прочтение
10 мин
Количество просмотров 114K
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Несказанно рад, что читателям понравилась предыдущая статья. Сразу сделаю оговорку — просто рассказать о таком ёмком понятии как тензор не получится — велик объем информации. Могу обещать, что к концу цикла мозаика сложится.
А в прошлый раз мы остановились на том, что рассмотрев представление вектора в косоугольном базисе, и определив, что он представляется двумя разными (ковариантными и контравариантными) наборами координат, получили общие выражения для скалярного произведения, учитывающие изменение метрики пространства. Таким образом, мы весьма осторожно подошли к понятию тензора
Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором >своих компонент и правилом преобразования компонент при смене базиса.
Скалярное произведение — это хорошо. Но как же быть с остальными операциями? Как они связываются с геометрией пространства и представимы ли в тензорном виде? Разумеется представимы, ведь векторы — это… тензоры! И скаляры — это тоже тензоры. Привычные нам математические объекты лишь частные примеры более общего понятия, коим является тензор.
Вот об этом мы и поговорим под катом.
1. Геометрический смысл метрического тензора
Для наглядности, которая не слишком повлияет на общность рассуждений, ограничимся трехмерным пространством. Докажем следующее утверждение — определитель метрического тензора равен квадрату объема параллелепипеда, натянутого на векторы базиса.
Рис. 1. Соотношения в трехгранном угле, образованном базисом
Рассмотрим произвольный базис
Вычислим объем параллелепипеда, натянутого на базис так, как это принято в стереометрии
где S — площадь основания параллелепипеда; h — высота, проведенная к данному основанию.
Площадь основания вычисляется тривиально — как модуль векторного произведения
С определением высоты придется повозится. Если бы мы знали угол , то легко нашли бы высоту
Угол связан с линейными и двугранными углами трехгранного угла
– первая теорема косинусов для трехгранного угла. Из нее выражаем косинус двугранного угла
Квадрат синуса необходимого нам угла выражаем через полученный косинус
Выполняем последовательные подстановки от (6) до (2), не забывая возвести в квадрат площадь S и высоту h. Выкладки достаточно громоздкие и для их выполнения можно воспользоваться СКА (Maple или Mathematica) и получить квадрат объема параллелепипеда
Теперь вычислим определитель метрического тензора. Им называется определитель матрицы, которая составлена из компонентов тензора. Входящие в нее скалярные произведения векторов базиса выпишем в явном виде
Вычислив его, получим тот же результат, что и для квадрата объема
Таким образом, утверждение (1) верно. Соответственно, объем параллелепипеда, натянутого на базис можно получить извлечением корня из определителя метрического тензора
где для краткости обозначим значение определителя.
Корень (7) часто встречается в литературе по ОТО и альтернативным теориям гравитации типа РТГ. Эта величина имеет фундаментальное значение и пригодится нам чуть позже.
2. Тензорное произведение векторов. Диада. Ранг тензора. Свертка
Обратим внимание на выражение скалятного произведения
Величину
называют тензорным произведением двух векторов или диадой. Тензорным это произведение названо потому что перемножаются тензоры и на выходе получается тензор, в данном случае второго ранга, . Ранг тензора — это количество его индексов. Вектор, внезапно, тоже является тензором, только первого ранга. Да это и понятно — ведь вектор, как геометрическая сущность, не зависит от системы координат, в которой его рассматривают. От выбора системы координат зависят лишь его компоненты.
Тензор второго ранга (8), разумеется, представлен матрицей своих компонент
Используя (8) можно переписать скалярное произведение в виде
это тоже тензорное произведение, называемое сверткой из-за того, что приводит к уменьшению ранга результирующего тензора. Все индексы в (10) «немые», по ним производится двойное суммирование компонент метрического тензора и диады и на выходе получатся число c.
Внимательный читатель скажет, что на выходе должен получится тензор. Так тензор и получается — скаляр, это тоже тензор. Нулевого ранга, так как не имеет индексов и не подлежит преобразованию при смене базиса. Скалярное произведение инвариантно относительно смены базиса, ибо ни длина участвующих в нем векторов ни угол между ними от смены базиса не меняются. Значит скаляр — это тензор нулевого ранга.
Но не любое число есть скаляр. Скаляр — это длина вектора, скалярное произведение векторов, масса материального тела, абсолютная температура и прочие величины, не зависящие от системы координат. Компонента вектора уже не является скаляром — она меняется при смене базиса.
О ранге тензоров и типе из компонент мы поговорим чуть позже, а пока перейдем к следующему животрепещущему вопросу.
3. Векторное произведение. Тензор Леви-Чивиты
Вернемся к нашим векторам и выполним их векторное умножение
За неимением других вариантов, аккуратно раскроем скобки, помня о некоммутативности операции
Разумеется мы хорошо учились в университете и знаем, что векторное произведение вектора самого на себя равно нулю. Но мы не будем сильно спешить с упрощением, ибо кроме этого, несомненно приятного факта, мы видим ещё одну вешь — компоненты диады (9). Но кроме упрощения связанного с нулевым произведением коллинеарных векторов мы больше ничего не наблюдаем. Мы работаем с произвольным базисом в чистом виде.
Применим хитрость — умножим вектор скалярно на первый вектор базиса
учтя теперь, что произведения
Коэффициенты в квадратных скобках — смешанные произведения векторов. Если векторы компланарны (лежат в одной плоскости) то такое произведение равно нулю. То есть, если в смешанном произведении повторяется хотя бы один вектор, оно равно нулю. Значит у нас остается только два слагаемых из девяти, в которых не повторяются векторы при смешанном умножении
Так, а теперь вспоминаем, что — ковариантная компонента вектора
. Ну и наконец переставим векторы в векторном произведении первого слагаемого, добавив минус как и положено по правилу векторного произведения
Аналогичным образом выделяем остальные компоненты
Выражения (11) — (13) очень напоминают формулы для расчета проекций векторного произведения из курса векторной алгебры, с точностью до множителя со смешанным произведением. Но мы-то работаем не в декартовом базисе, естественно ожидать некоторое отличие. Кстати, а что это за множитель? Ведь смешанное произведение векторов имеет геометрический смысл… Это же… объем параллелепипеда, натянутого на векторы в нем участвующие. А объем параллелепипеда, натянутого на базис это ведь корень из определителя метрического тензора! То есть
Вот она и всплыла на поверхность, метрика используемого пространства. Таким образом, можно построить некий тензор, свертка исходных векторов с которым дает ковариантный вектор, являющийся результатом векторного произведения. Более того, этот тензор связан с метрическим тензором. Таковой тензор третьего ранга носит имя итальянского математика Леви-Чивиты.
Не трудно увидеть, что компоненты тензора Леви-Чивиты определяются соотношением
Их будет 27, но большинство из них, а именно 21 равны нулю. Это те компоненты, индексы которых повторяются хотя бы один раз. Ненулевых компоненты только шесть, они соответствуют не повторяющимся индексам. По модулю они равны , но три из них положительны, другие три отрицательны. В формулах (11) — (13) мы переставили векторы местами и добавили минусы, чтобы сделать коэффициенты при диадах положительными а сами формулы похожими на привычные нам по курсу векторной алгебры. Теперь вернем всё на свои места
Знак смешанных произведений зависит от порядка индексов: в наборах (1,2,3), (2,3,1), (3,1,2) они положительны, в наборах (1,3,2), (2,1,3) и (3,2,1) — отрицательны. Известно, что если векторы заданы в правой системе координат, то их смешанное произведение будет положительно, если они образуют правую тройку векторов. В первых слагаемых (16) — (18) фигурируют правые тройки векторов базиса. Во вторых слагаемых, в смешанном произведении участвуют те же векторы, но взятые как левая тройка.
Как определить, какую тройку дают базисные векторы? Очень просто, ведь они упорядочены, им присвоены номера 1, 2, 3. Если мы соблюдаем порядок следования векторов, мы получаем тройку, соответствующую используемой системе координат, то есть (1,2,3) — правая тройка.
А если первым мы берем вектор 2? То за ним должен следовать вектор 3, по порядку. А какой следующий? А следующий вектор 1, начинаем всё сначала, но не нарушая порядка следования векторов, то есть и (2,3,1) — правая тройка, ну и (3,1,2) — тоже правая тройка. Говоря языком комбинаторики — базисные векторы в упорядоченной тройке образуют четную перестановку (то есть не нарушающую порядок следования элементов). Если порядок следовая векторов в тройке обратный принятому, то их перестановка будет нечетной. Таким образом перестановки (3,2,1), (2,1,3), (1,3,2) — нечетные, а тройки векторов — левые.
Используя всё вышесказанное, введем функцию
и, на основании (14) и (19) наконец выпишем тензор Леви-Чивиты
для правой системы координат
для левой системы координат.
После этого можно выписать выражение для векторного произведения в тензорном виде
Таким образом — векторное произведение, это свертка диады тензором Леви-Чивиты, дающая на выходе ковектор — то есть вектор, заданный ковариантными компонентами.
4. Смешанное (векторно-скалярное) произведение векторов
Вооружившись полученными знаниями рассмотрим теперь такую операцию
Не оперируя векторами, попробуем сразу записать её в тензорном виде. Во-первых, скалярное произведение коммутативно, поэтому
А теперь вспомним, что скалярное произведение можно расписать как тензорное
произведение ковектора на вектор
Векторное произведение, исходя из (21)как раз и дает ковектор, а значит
То есть, окончательно, смешанное произведение в тензорной форме
где снова участвует тензор Леви-Чивиты.
Выражение (22) можно было получить оперируя векторами, выйдя опять на определение тензора Леви-Чивиты, но, как видно, рациональнее использовать тензорную запись.
5. Ранг тензора. Ковариантные и контравариантные компоненты
Итак, в процессе разбора векторных операций мы пришли к выводу, что тензоры — это математические объекты, обобщающие свойства и операции над многими, известными нам математическими объектами. Тензорами являются и скаляры и векторы. Различаются они рангом и количеством ковариантных и контравариантных компонент. Ранг равен общему числу индексов тензора, а обозначается он парой целых чисел в скобках (p, q), где p — число контравариантных индексов, q — число ковариантных индексов. Говорят что тензор — p-раз контравариантный и q-раз ковариантный, ранга p+q.
- Тензор ранга (0,0) — это скаляр, величина, значение которой может быть выражено одним числом, со значением инвариантным относительно смены системы координат. У скаляра нет индексов, и он вообще не преобразуется при смене базиса. Но, повторимся, не всякое число есть скаляр. Так например, компонент вектора или тензора не есть скаляр, ибо он изменяется при смене базиса.
- Тензор ранга (1,0) — вектор. Для вектора естественно контравариантное представление, для вычисления скалярного произведения векторов требуется их свертка с метрическим тензором.
Преобразование компонент вектора производится путем применения к нему линейного оператора, по сути умножением матрицы преобразования на столбец, содержащий компоненты вектора, что в тензорной форме выглядит как
- Тензор ранга (0,1) — ковектор. Если в рассматриваемом пространстве определен невырожденный метрический тензор
то вектор и ковектор — это два разных представления одного и того же геометрического объекта — вектора. В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором
где
контрвариантный метрический тензор, компоненты которого — матрица,
обратная матрице компонент тензора.
Для скалярного умножения ковектора на вектор не нужно использовать метрический тензор, оно производится прямой сверткой с вектором.
Преобразование компонент ковектора так же производится путем применения к нему линейного оператора, но в отличие от вектора, производится умножение строки, содержащей компоненты ковектора на матрицу преобразования координат
- Тензор ранга (0,2) — билинейная форма, примером которой может служить дважды ковариантный метрический тензор gij. Компоненты метрического тензора преобразуются путем двукратного применения к нему линейного оператора преобразования координат, что соответствует умножению транспонированной матрицы преобразования на матрицу метрического тензора и последующему умножению результата на матрицу преобразования
- Тензор ранга (2,0) — примером может служить диада (8). Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
операторов, преобразующих исходные векторы. - Тензор ранга (1,1) — линейный оператор. Примером может служить матрица поворота или любого другого преобразования координат векторов и ковекторов. Вообще, применение линейного оператора сводится к операции матричного умножения
где
— результат преобразования;
— исходный вектор;
— компоненты матрицы линейного оператора. Рассмотрим процесс преобразования линейного оператора. Пусть S матрица перехода от одно базиса к другому. Тогда, при смене базиса преобразуются оба вектора — и аргумент и результат
Подставляя (24) в (23) получаем
откуда, умножая слева на матрицу
получаем
где
— компоненты матрицы
. С другой стороны, для векторов в новом базисе справедливо
сравнивая (25) и (26), получаем выражение преобразования линейного оператора
Все перечисленные объекты обладают общностью свойств: имеют набор компонент и правило преобразования при смене базиса.
Выводы
Подведем некоторые итоги.
Во-первых, мы выяснили, что векторные операции могут быть сведены к тензорным соотношениям, что избавляет нас от неудобства каждый раз выводить формулы для них при использовании экзотической системы координат или увеличении размерности пространства. Соотношения останутся прежними, изменится только внутренность тензоров, связанных с геометрией пространства и выбором положительного направления вращения в нем. Учитывая, что многие уравнения физики, математики и механики оперируют векторными величинами, использование тензоров позволяет записать уравнения лишь однажды. Кроме того, тензорная запись компактна — это упрощает проведение выкладок.
Во-вторых, мы понимаем, что многие математические объекты — скаляры, векторы, билинейные формы, линейные операторы — всё это частные случаи тензоров, а значит их свойства могут быть обобщены под могучим крылом своего более сложного собрата-тензора.
В дальнейшем мы увидим, как тензорная запись позволяет подходить к весьма прозаичным вопросам с общих позиций, облегчая жизнь исследователю.
Продолжение следует…



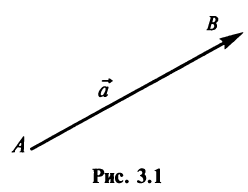
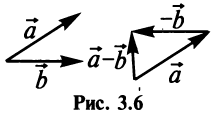
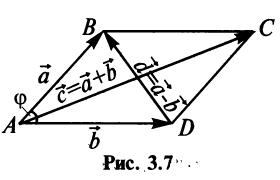
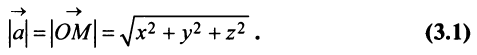
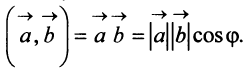
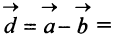
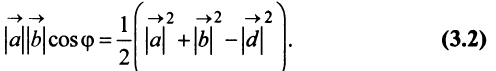
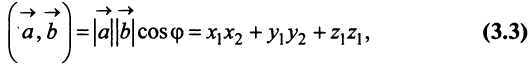
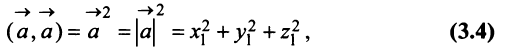
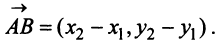
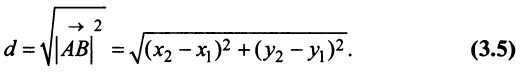
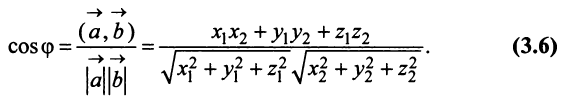
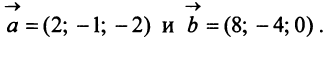
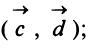
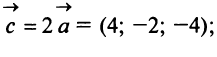
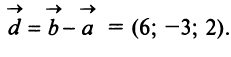
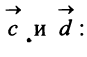
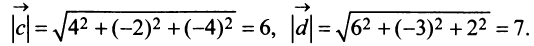
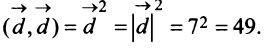
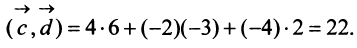
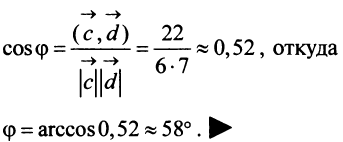
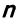 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство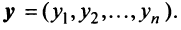
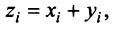
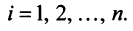
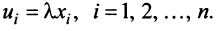
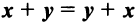 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: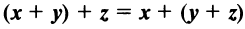 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы;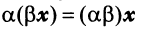 — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;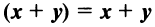 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;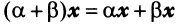 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;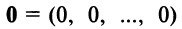 такой, что
такой, что 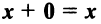 для любого вектора
для любого вектора 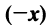 такой, что
такой, что 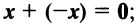
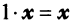 для любого вектора
для любого вектора 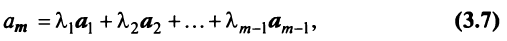
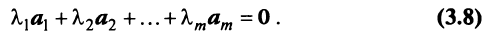
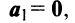 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 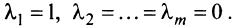
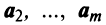 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 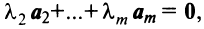 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 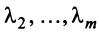 и
и 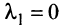 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).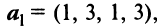
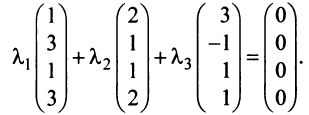
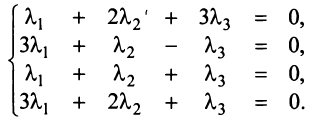
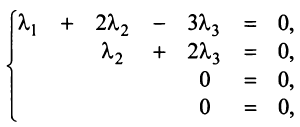
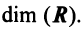
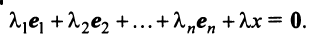
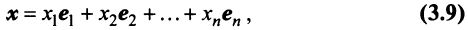
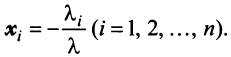
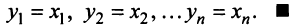
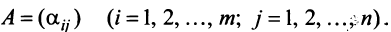


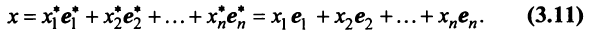
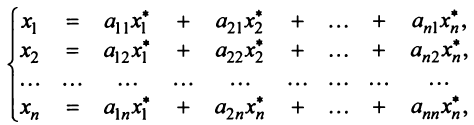
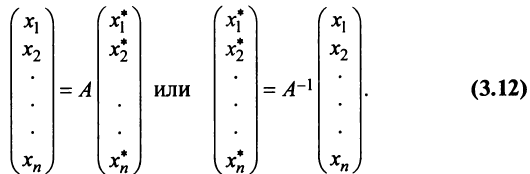
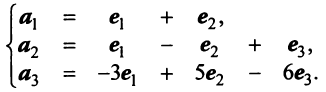
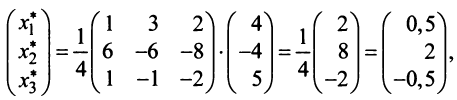
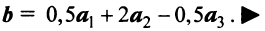
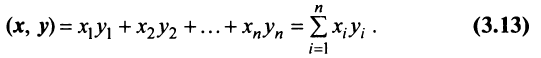
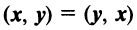 — коммутативное свойство;
— коммутативное свойство;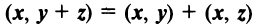 — дистрибутивное свойство;
— дистрибутивное свойство;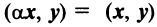 — для любого действительного числа;
— для любого действительного числа;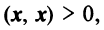 если
если  — ненулевой вектор;
— ненулевой вектор; 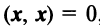 , если
, если