Калькулятор квадратных уравнений
Калькулятор вычислит любой тип квадратного уравнения, включая неполные квадратные уравнения, найдет действительные и комплексные корни, а также построит график и найдет точки пересечения параболы с осью x.
Квадратное уравнение
ax² + bx + c = 0
где a, b, c — коэффициенты квадратного уравнения и a≠0
a — первый или старший коэффициент
b — второй или средний коэффициент
c — свободный член
Дискриминант квадратного уравнения D определяет количество корней и их тип: вещественные либо комплексно-сопряженные.
Дискриминант вычисляется по формуле:
D = b2-4ac
Если
D
=
0
, уравнение имеет единственный корень.
x
=
− b 2a
Например, уравнение
x2+2x+1
=
0
Значения коэффициентов
a
=
1
b
=
2
c
=
1
Дискриминант
D
=
b2-4ac
D
=
2 2 — 4 · 1 · 1
=
0
x
=
− b 2a
x
=
− 22 · 1
=
-1
x
=
-1
График
y
=
x2+2 · x+1
Решением квадратного уравнения является пересечение параболы с осью x. Так как уравнение имеет один корень, то парабола на графике пересекает ось x только в одной точке.
Если
D
>
0
, уравнение имеет два различных корня.
x1
=
— b — D 2 a
x2
=
— b + D 2 a
Например, уравнение
2x2+5x+3
=
0
Значения коэффициентов
a
=
2
b
=
5
c
=
3
Дискриминант
D
=
b2-4ac
D
=
5 2 — 4 · 2 · 3
=
1 > 0
x1
=
— 5 — 1 2 · 2
=
-32
x2
=
— 5 + 1 2 · 2
=
-1
x1
=
-32
=
-1.5
x2
=
-1
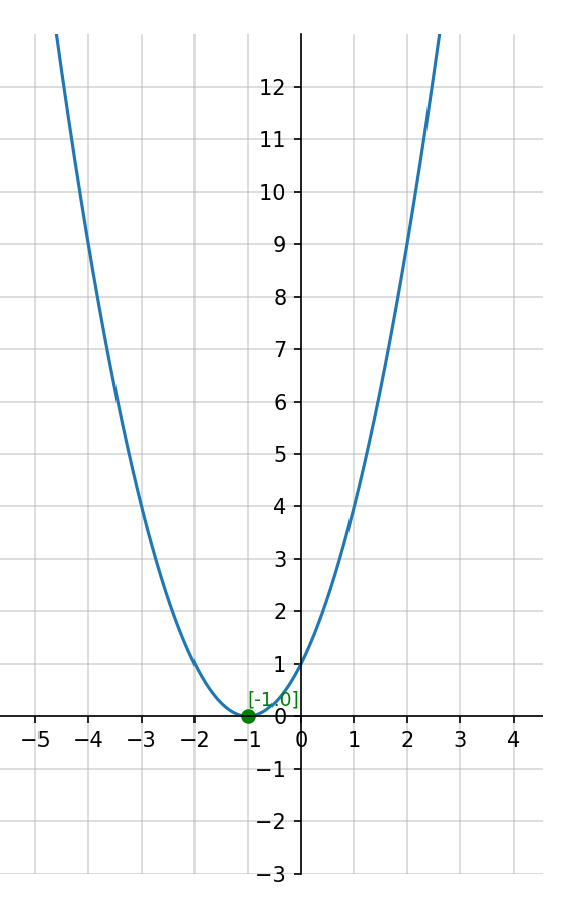
График
y
=
2x2+5x+3
Решением квадратного уравнения является пересечение параболы с осью x. Так как уравнение имеет два корня, то парабола на графике пересекает ось x в двух точках.
Если
D
<
0
, уравнение имеет два комплексно-сопряжённых корня, выражающихся той же формулой, что и для положительного дискриминанта.
x1
=
— b — D 2 a
x2
=
— b + D 2 a
Например, уравнение
3x2-x+7
=
0
Значения коэффициентов
a
=
3
b
=
-1
c
=
7
Дискриминант
D
=
b2-4ac
D
=
-1 2 — 4 · 3 · 7
=
-83 < 0
x1
=
— b — D 2 a
x2
=
— b + D 2 a
x1
=
— -1 — -83 2 · 3
=
16-83 · i6
x2
=
— -1 + -83 2 · 3
=
16+83 · i6
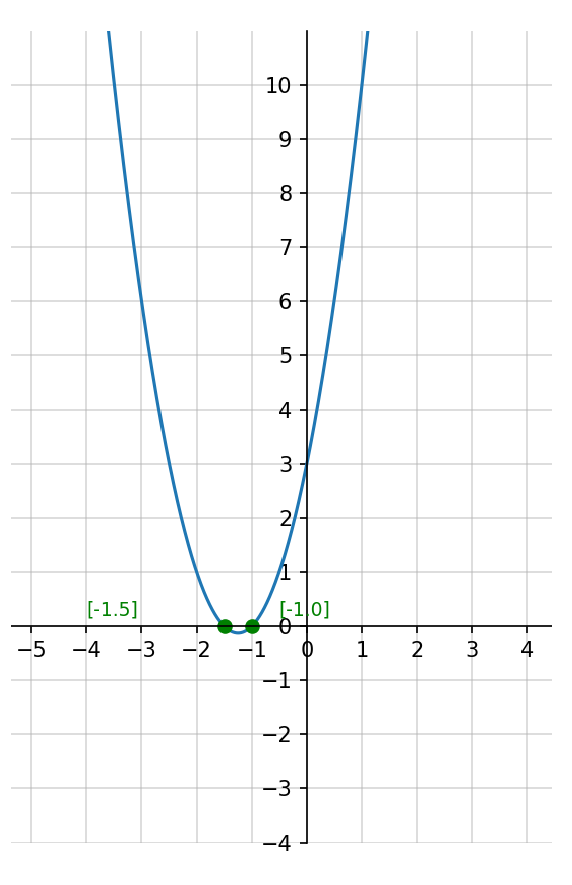
График
y
=
3x2-x+7
Обратите внимание на параболу графика, она не пересекает ось x, следовательно, уравнение не имеет действительных корней.
Неполные квадратные уравнения
Неполное квадратное уравнение характеризуется тем, что хотя бы один из коэффициентов b или c равен нулю.
Уравнение ax² + bx = 0
Разберем на примере уравнения
2x2+6x
=
0
Значения коэффициентов
a
=
2
b
=
6
Неполное квадратное уравнение вида ax² + bx = 0, где b≠0 имеет два действительных корня:
x1
=
0
и
x2
=
− ba
Решение
x1
=
0
x2
=
− 62
=
-3
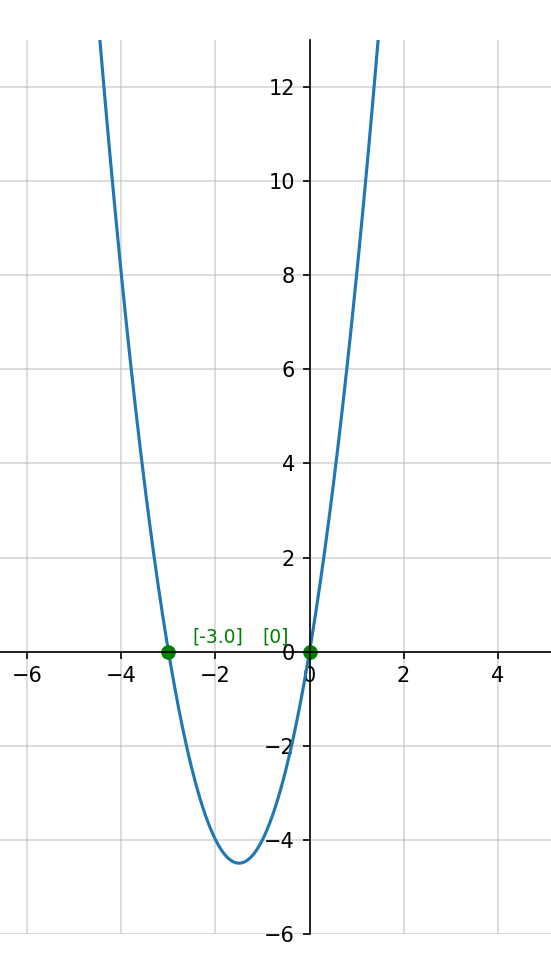
График
y
=
2x2+6x
Уравнение ax² + c = 0
Разберем на примере уравнения
x22-5
=
0
Значения коэффициентов
a
=
12
c
=
-5
Неполное квадратное уравнение вида ax² + c = 0 и имеет два действительных корня в том случае, если
c a < 0
и два комплексных корня если
c a > 0
.
ca
=
-512
=
-10
Решение
c a < 0
, уравнение имеет два различных корня:
x1
=
— — c a
x2
=
— c a
x1
=
— — -5 12
=
-10
x2
=
— -5 12
=
10
x1
=
-10
=
-3.16227766016838
x2
=
10
=
3.16227766016838
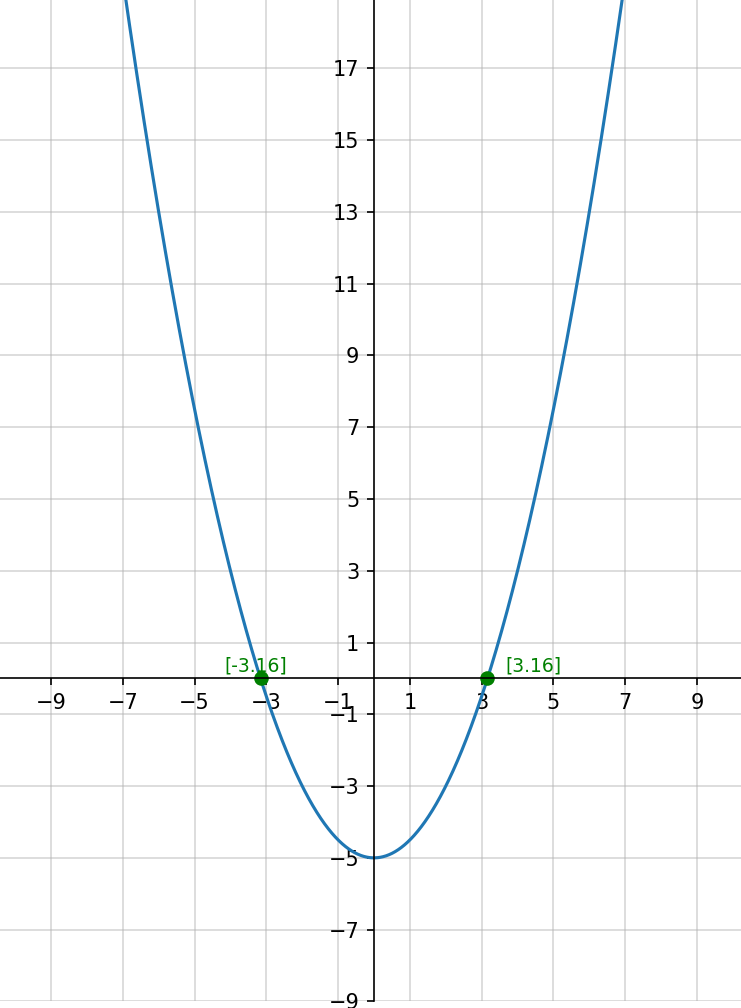
График
y
=
x22-5
| Укажите коэффициенты a b и c квадратного уравнения ax2 + bx + c = 0 | |||||
|
|
|||||
| x2 + | x + | = 0 | |||
|
|
Что такое квадратное уравнение
Уравнение вида ax2 + bx + c = 0 называется квадратным.
Решить квадратное уравнение означает найти его корни, а именно x1 и x2, либо установить, что корней нет.
Числа a, b, c — называются коэфициентами квадратного уравнения, где a ≠ 0.
a — старший коэфициент
b — средний коэфициент
c — свободный член
Если коэфициент b или c или оба этих коэфициента равны нулю, то такое уравнение называется неполным.
Дискриминант квадратного уравнения D выражается следующей формулой D = b2 — 4ac.
Как решить квадратное уравнение
Прежде всего при решении квадратного уравнения необходимо найти его дискрименант.
Если D > 0, то уравнение имеет два действительных корня, которые можно найти по формуле:
Приведем пример, решим уравнение 5x2 + 67x + 7 = 0
Найдем дискриминант D квадратного уравнения 5x2 + 67x + 7 = 0. В данном уравнении a = 5; b = 67; c = 7, тогда
D = b2 — 4ac = 672 — 4 · 5 · 7 = 4349
Дискриминант уравнения больше нуля, следовательно, уравнение имеет два корня.
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
Если D = 0, то корни квадратного уравнения равны, по сути уравнение имеет один корень, например 9x2=0. При D = 0 необходимо воспользоваться формулой:
Приведем пример, решим уравнение x2 + 2x + 1 = 0
Найдем дискриминант D квадратного уравнения 1x2 + 2x + 1 = 0. В данном уравнении a = 1; b = 2; c = 1, тогда
D = b2 — 4ac = 22 — 4 · 1 · 1 = 0
Дискриминант уравнения равен нулю, следовательно, уравнение имеет один корень.
Если D < 0, то уравнение не имеет действительных корней и корнями уравнения могут быть только комплексные числа, например, 5x2 + 6x + 7 = 0, 20x2 + 2x + 3 = 0.
При D < 0 необходимо воспользоваться формулой:
Приведем пример, решим уравнение 3x2 — 2x + 7 = 0
Найдем дискриминант D квадратного уравнения 3x2 — 2x + 7 = 0.
В данном уравнении a = 3; b = -2; c = 7, тогда
D = b2 — 4ac = (-2)2 — 4 · 3 · 7 = -80
Дискриминант меньше нуля, следовательно, уравнение не имеет действительных корней. Корнями уравнения могут быть только комплексные числа.
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
| 0.333333333333333 + (1.49071198499986)i | ||
| 0.333333333333333 — (1.49071198499986)i | ||
Комплексные корни являются результатом решения квадратных уравнений с комплексными коэффициентами вида: а х X2 + b х X + c = 0. Онлайн калькулятор осуществляет решение в два последовательных шага.
На первом шаге по формуле D = b2 – 4 х a х c высчитывается дискриминанта. Затем по формуле
X 1,2 = (- b +- (корень (D)) / 2 х a
вычисляются корни, которые, как и коэффициенты a,b, c, а также дискриминанта D, являются комплексными числами.
Потребность в вычислении квадратных уравнений с получением комплексных корней является востребованной задачей не только в математике, но и во многих прикладных направлениях. В физике при решении различных задач, и электротехнике при изучении переменного однофазного и трехфазного тока методика решения квадратных уравнений помогает получать быстрые достаточно точные результаты.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Квадратное уравнение с комплексными коэффициентами
| Аргументы квадратного уравнения |
| Точность вычисления (знаков после запятой) |
| Вы ввели следующее выражение |
| Результат решения заданного уравнения |
Расчет квадратных уравнений, содержащие комплексные коэффициенты
Как известно, квадратное уравнение: 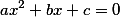

Онлайн решений очень много, наш же бот, вычисляет квадратное уравнение, если его коэффициенты являются комплексными числами.
В русскоязычном секторе Интернета, такого сервиса нет, и наш бот будет тут первым.
Хотелось бы заметить, что коэффициентами квадратного уравнения могут быть не только комплексные числовые значения, но и произвольное комплексное выражение. Это несомненно расширяет возможности представленного сервиса, и дает определенные преимущества.
Ну и естественно, для тех кто хорошо учился в школе, и понимающих, что комплексные числа это лишь расширенное представление наших «обычных» действительных чисел, следует вывод, что данный сервис правильно считает и в том случае, если числа в коэффициентах имеют действительные значения.
Для того, что бы по известным корням можно было построить произвольное уравнение, в том числе и квадратное с комплексными коэфициентами можно воспользоватся ресурсом Создание полинома (многочлена) одной переменной онлайн
Синтаксис
Для всех кто пользуется XMPP клиентами: ur2_i <элементы уравнения>
Коэффициенты уравнения могут быть как действительными так и мнимыми значениями.
Более того, каждый коэффициент может быть выражен не только числом, но и каким либо выражением
Элементы уравнения вводятся по принципу слева направо, от элемента с более высокой степенью переменной х, к более низкой.
Каждый элемент уравнения должен быть разделен пробелами.
Примеры
Пишем в поле ввода коэффициенты
4 8-i -i
Не забудьте, что как минимум одним пробелом разделяются эти значения
ответ будет следующий
| Вы ввели следующее выражение |
*x^2+(8-i)*x^1+(-i)=0) |
| Результат решения заданного уравнения |
|
Решаем комплексное уравнение: x^2 + (2-0.25i)*x + (0-0.25i)= 0 |
Давайте проверим, а правильно ли нам посчитал бот эти корни. Для этого воспользуемся Аргумент и значения функции комплексной переменной и посчитаем чему же будет равно значение функции, при полученных корнях
При выборе первого корня ответ будет такой:
| Вы ввели следующую функицю | ||||
=x^2%20+%20(2-0.25i)*x%20+%20(0-0.25i)) |
||||
| Табличное представление значений функции | ||||
|
Несмотря на небольшую погрешность, результат говорит нам о том что расчеты проведены верно
Здесь мы видим, что коэффициенты представлены в виде комплексных выражений, но для бота это не помеха.
пишем в запросе
2-i ln(1+sin(i)) -3
и получаем результат
| Вы ввели следующее выражение |
*x^2+(ln(1+sin(i)))*x^1+(-3)=0) |
| Результат решения заданного уравнения |
|
Решаем комплексное уравнение: x^2 + (0.0003584355453+0.4330639593925i)*x + (-1.2-0.6i)= 0 |
Удачи в расчетах!
Комплексные числа по-шагам

Примеры комплексных выражений
- Деление комплексных чисел
-
(1-2i)/(1+4i)
- Умножение комплексных чисел
-
(5+4i)*(8-2i)
- Комплексные уравнения
-
z - |z| = 2 + i
-
(i + 5)*z - 2*i + 1 = 0
- Возведение комплексного числа в степень
-
i^15
-
(1 - 2*i)^32
- Квадратный корень из комплексного числа
-
sqrt(1-24*i)
- Кубический корень
-
cbrt(1-24*i)
- Корни четвертой и пятой степени
-
(1-11*i)^(1/4)
-
(1-11*i)^(1/5)
- Мнимая и действительная часть
-
im(re(x) + y)
- Комплексно-сопряженное число
-
conj(1 + 4j)
-
(3/2-3*sqrt(3)/2*i)/conj(-5/2-1/3*i)
- Реальная часть комплексного числа
-
re(1+I)
- Мнимая часть
-
im(1+I)
- Модуль комплексного числа
-
absolute(1+I)
- Аргумент
-
arg(1+I)
- Комплексный знак числа
-
sign(1+I)
Что умеет?
- Простые операции с комплексными числами
- Выполнять деление с подробным решением
- Находить разные формы комплексных чисел:
- Алгебраическую
- Тригонометрическую
- Показательную
- Модуль и аргумент комплексного числа
- Комплексно-сопряжённое к данному
- Геометрическую интерпретацию комплексного числа
Подробнее про Комплексное число
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности

x%20-i%20=%200)
x^2%20+%20ln(1+sin(i))x%20-3%20=%200)