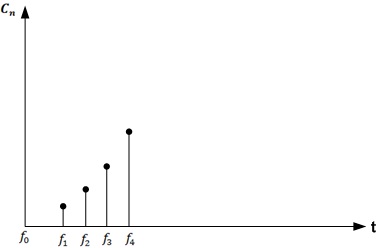
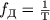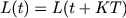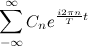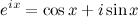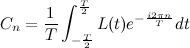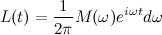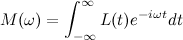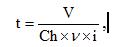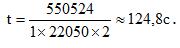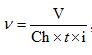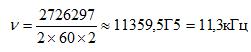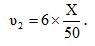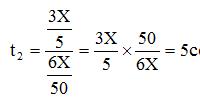Автор материалов — Лада Борисовна Есакова.
При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.
Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).
Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).
Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).
Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).
Количество уровней дискретизации d можно рассчитать по формуле: d = 2B.
Тогда объем записанного файла V(бит) = f * B * k * t.
Или, если нам дано количество уровней дискретизации,
V(бит) = f * log2d * k * t.
Единицы измерения объемов информации:
1 б (байт) = 8 бит
1 Кб (килобайт) = 210 б
1 Мб (мегабайт) = 220 б
1 Гб (гигабайт) = 230 б
1 Тб (терабайт) = 240 б
1 Пб (петабайт) = 250 б
При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.
Если X – количество точек по горизонтали,
Y – количество точек по вертикали,
I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2I. Соответственно, I = log2N.
Тогда объем файла, содержащего изображение, V(бит) = X * Y * I
Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log2N.
Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).
Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.
Кодирование звука
Пример 1.
Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 30 2) 45 3) 75 4) 90
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223
Переведем все величины в требуемые единицы измерения:
V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 223
Представим все возможные числа, как степени двойки:
V(Мб) = (24 * 23 * 125 * 25 * 2 * 22 * 3 * 15 * 22) / 223 = (5625 * 217) / 223 = 5625 / 26 =
5625 / 64 ≈ 90.
Ответ: 4
!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.
!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 210. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.
Пример 2.
В течение трех минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 КГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 25 Мбайт
2) 35 Мбайт
3) 45 Мбайт
4) 55 Мбайт
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223 = (16 * 1000 * 24 * 4 * 3 * 60) / 223 = (24 * 23 * 125 * 3 * 23 * 22 * 3 * 15 * 22) / 223 = (125 * 9 * 15 * 214) / 223 = 16875 / 29 = 32, 96 ≈ 35
Ответ: 2
Пример 3.
Аналоговый звуковой сигнал был записан сначала с использованием 64 уровней дискретизации сигнала, а затем с использованием 4096 уровней дискретизации сигнала. Во сколько раз увеличился информационный объем оцифрованного звука?
1) 64
2) 8
3) 2
4) 12
Решение:
V(бит) = f * log2d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.
V1 = f * log264 * k * t = f * 6 * k * t
V2 = f * log24096 * k * t = f * 12 * k * t
V2 / V1 = 2
Правильный ответ указан под номером 3.
Ответ: 3
Кодирование изображения
Пример 4.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
V (Кб) = (64 * 64 * log2256) / 213 = 212 * 8 / 213 = 4
Ответ: 4
Пример 5.
Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
log2N = V /( X*Y) = 213 / (26 * 25) = 4
N = 16
Ответ:16
Сравнение двух способов передачи данных
Пример 6.
Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать.
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
– средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
– объем сжатого архиватором документа равен 80% от исходного,
– время, требуемое на сжатие документа – 35 секунд, на распаковку – 3 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.
Решение:
Способ А. Общее время складывается из времени сжатия, распаковки и передачи. Время передачи t рассчитывается по формуле t = V / q, где V — объём информации, q — скорость передачи данных.
Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 223 бит.
Найдём общее время: t = 35 с + 3 с + 4 * 223 бит / 218 бит/с = 38 + 27 с = 166 с.
Способ Б. Общее время совпадает с временем передачи: t = 5 * 223 бит / 218 бит/с = 5 * 25 с = 160 с.
Способ Б быстрее на 166 — 160 = 6 с.
Ответ: Б6
Определение времени передачи данных
Пример 7.
Скорость передачи данных через ADSL─соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.
Решение:
Время t = V / q, где V — объем файла, q — скорость передачи данных.
t = 625 * 210 байт / (2 7 * 1000) бит/c = 625 * 213 бит / (125 * 210) бит/c = 5 * 23 с = 40 с.
Ответ: 40
Пример 8.
У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 215 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 4 Мбайта по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Нужно определить, сколько времени будет передаваться файл объемом 4 Мбайта по каналу со скоростью передачи данных 215 бит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 217 бит/с).
Время скачивания данных Петей: t1= 4*223 бит / 215 бит/с = 210 c.
Время задержки: t2 = 512 кб / 217 бит/с = 2(9 + 10 + 3) — 17 c = 25 c.
Полное время: t1 + t2 = 210 c + 25 c = (1024 + 32) c = 1056 c.
Ответ: 1056
Пример 9.
Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 219 бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Полное время складывается из времени передачи из пункта А в пункт Б (t1), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t3).
t1 = (60 * 223) / 219 =60 * 16 = 960 c
t2 = 25 c
t3 = (60 * 223) / 220 =60 * 8 = 480 c
Полное время t1 + t2 +t3 = 960 + 25 + 480 = 1465 c
Ответ: 1465
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №9. Кодирование звуковой и графической информации. Передача информации, Время записи звукового файла, время передачи данных, определение объема информации.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Аналого-цифровое преобразование сигнала для начинающих
Время на прочтение
3 мин
Количество просмотров 184K
Вступление
Темы аналого-цифрового и цифро-аналогового преобразований являются достаточно важными в курсе электроники, поскольку большинство устройств, взаимодействующих с компьютером, имеют аналоговый вход/выход, а компьютер умеет обрабатывать исключительно цифровые сигналы. В этой статье я хочу поделиться с вами самыми основами таких преобразований.
Типы сигналов
Прежде чем разбираться в самих преобразованиях нужно знать, какие сигналы существуют. А их 3 типа:
- Аналоговые
- Дискретные
- Цифровые
Аналоговые – это сигналы непрерывные во времени, они определены во все моменты времени.
Дискретные – это сигналы представленные последовательностью отсчётов, т.е. значениями сигналов в дискретные моменты времени.
Цифровые – это сигналы дискретные во времени (или в пространстве) и квантованные по уровню. Вычислительные процедуры в компьютере выполняются именно в цифровых сигналах.
Для того, что бы компьютер мог выполнить обработку сигнала необходимо выполнить преобразование сигнала из аналоговой формы в цифровую.
После обработки выполняется обратное преобразование, поскольку большинство бытовых устройств управляются аналоговыми сигналами.
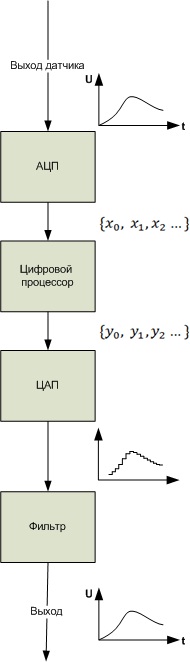
Структурная схема цифровой обработки сигнала в общем виде выглядит следующим образом:
Аналого-цифровое преобразование сигнала
Аналого-цифровое преобразование сигнала включает в себя два этапа:
- Дискретизация сигнала (во времени или пространстве)
- Квантование по уровню
На этапе дискретизации берутся отсчёты сигнала с некоторым периодом дискретизации (Т).
Частоту дискретизации можно определить по формуле
Процесс получения отсчёта входного сигнала должен занимать очень малую часть периода дискретизации, что бы снизить динамические ошибки преобразования, обусловленные изменением сигнала за время снятия отсчёта.
Частота дискретизации выбирается из теоремы Котельникова. В ней утверждается, что для того что бы по отсчётам сигнала можно было бы сколь угодно точно восстановить непрерывный сигнал необходимо что бы частота дискретизации не менее чем в два раза превосходила верхнюю частоту спектра дискретизируемого сигнала.
Любой сигнал имеет своё спектральное представление. Любое представление сигнала – это представление в виде суммы (или интеграла) гармонических составляющих (синусоид и косинусоид), различных частот взятых с определёнными весовыми коэффициентами (имеющими определённую амплитуду)
Для периодических сигналов это сумма, для непериодический – интеграл.
Переход к спектру сигнала осуществляется с помощью прямого преобразования Фурье.
Рассмотрим переход к спектральному представлению в виде периодической функции:
Как известно периодическая функция удовлетворяющая условию Дирихле может быть представлена рядом гармонических функций.
По формуле Эйлера любое выражение можно представить в виде
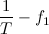
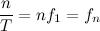
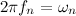

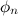
Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз называется фазовым спектром.
Пример спектра:
Для непериодический функции 
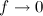
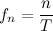
Прямое преобразование Фурье для непериодического сигнала
Таким образом спектр непериодической функции представляется суммой бесконечного количества гармонических колебаний, частоты которых расположены бесконечно близко друг к другу.
Квантование сигнала по уровню
Количество уровней квантования определяется по формуле
n — количество разрядов
N — уровень квантования
Выбор количества уровней квантования сигналов производится на основе компромиссного подхода, учитывающего с одной стороны необходимость достаточно точного представления сигнала, что требует большого числа уровней квантования, а с другой стороны количество уровней квантования должно быть меньше, что бы разрядность кода была минимальной.
На этом я закончу свою статью, что бы не перегружать читателя лишней информацией. Удачи в начинаниях!
На этой странице вы узнаете:
- Чем звуковая “лесенка” удобнее звуковой волны?
- От чего зависит качество вашей любимой музыки и звук при звонке?
- Для чего нужны каналы записи?
Дискретизация по времени и уровни громкости
Звук — это волна, высота которой непрерывно изменяется во времени.
В случае с радугой — если взять на ней две разные точки, они будут иметь разные оттенки, пусть и неразличимые человеческим глазом. В случае со звуком — две любые точки на волне будут разной высоты, пусть человеческое ухо и не почувствует разницы.
Поэтому для кодирования звукового файла также необходимо применять дискретизацию (подробнее о которой можно прочитать в статье «Дискретное представление информации»), причем не одну.
- Дискретизация по громкости превратит волну звука в “лесенку” — вместо постоянно меняющейся высоты волны мы будем иметь конкретные уровни громкости, которые будут приближенно равны высоте волны в разные моменты времени.

Каждый уровень кодируется определенным количеством бит, которое определяется глубиной кодирования (битовой глубиной/разрешением). Чем она больше, тем больше у нас будет уровней громкости.
Зависимость количества уровней громкости N от глубины кодирования i будет
N = 2 ^ i.
- Дискретизация по времени определяет, сколько именно раз в секунду будет производиться измерение текущего уровня громкости. Количество измерений в одной секунде — частота дискретизации, измеряется в Гц, а в реальности, когда ее значение становится очень большим — в кГц (1 кГц = 1000 Гц).
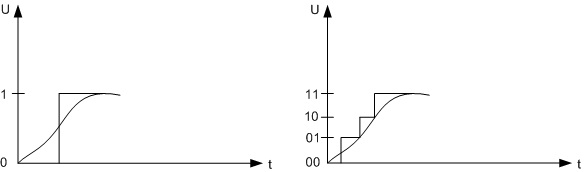
После проведения дискретизации по времени и по громкости вся звуковая волна превратится в “лесенку”:
— каждая “ступенька” определяет громкость звука в каждый отдельный момент времени (возможная высота ступеньки определяется глубиной кодирования звука);
— каждая секунда аудиозаписи будет разбита на конкретное число ступенек, определяемое частотой дискретизации.
И в таком формате кодирование звука не представляет собой никаких проблем, так как мы можем кодировать отдельные “ступеньки”.
Например, следующая звуковая волна была разбита с глубиной кодирования, равной 3 битам (поэтому уровней громкости ровно 2 ^ 3 = 8 и каждый закодирован кодом, длиной в 3 символа) и частотой дискретизации 4 Гц.

Чем больше будут значения глубины кодирования и частоты дискретизации, тем больше “лесенка” будет похожа на оригинальную волну.
Если поднять значения из примера выше всего в несколько раз, результат уже будет гораздо более похожим на оригинальную волну:

В реальности эти параметры могут достигать еще больших значений:
- минимальным значением частоты дискретизации для передачи человеческой речи считается 8000 Гц, оно используется в телефонной связи, а в студиях звукозаписи может принимать значение 192 000 Гц и даже больше;
- достаточной глубиной кодирования звука считается значение 16 бит, при котором появляется уже 2 ^ 16 = 65536 уровней громкости, но для профессиональных работ это значение может доходить и до 32 бит.
Количество каналов. Формула объема звука
Нельзя также забывать про такую характеристику звука, как объемность:
- при прослушивании музыки в наушниках иногда можно услышать, что какие-то музыкальные инструменты громче звучат с одной стороны, а другие — с другой;
- в кинотеатре в масштабных сценах с большим количеством событий можно услышать, что действия, происходящие на экране справа, звучат громче справа, а происходящие слева — громче слева. А иногда и сзади что-нибудь произойдет.
Объемность звуку придает количество каналов записи, когда в одном файле находится несколько звуковых волн, которые воспроизводятся одновременно. Программы воспроизведения обрабатывают их и выдают звук там, где он должен был быть.
Например, чтобы озвучить падение двух камней с двух разных сторон, нужно иметь оба звука и воспроизводить их вместе, но с разных колонок или через разные наушники.

Так как каждый новый канал добавляет в аудиофайл буквально новые звуковые волны, каждую из них также придется закодировать по тем же параметрам, поэтому количество каналов прямо пропорционально будет увеличивать объем файла.
Количество каналов обозначается специальными словами:
- моно — 1 канал;
- стерео — 2 канала;
- квадро — 4 канала.
Осталось вспомнить, что у записи звука есть еще и продолжительность, и мы имеем все данные, чтобы найти вес звукового файла:
- глубина кодирования i — вес одного уровня звука;
- частота дискретизации F — количество кодируемых уровней громкости в 1 секунде;
- продолжительность t;
- количество каналов записи N.
Полный вес аудиофайла V будет равен произведению всех этих параметров: V = F * B * t * N.
Фактчек
- Глубина кодирования определяет количество бит, выделяемое на хранение одного уровня громкости, на которые будет разделена звуковая волна по высоте;
- Частота дискретизации обозначает дискретизацию звука по времени — сколько уровней громкости будет закодировано в 1 секунде;
- Количество каналов определяет объемность звука, добавляя в 1 файл несколько звуковых волн, поэтому прямо пропорционально увеличивает вес всего файла.
Проверь себя
Задание 1.
Количество уровней громкости зависит от…
- дискретизации по времени
- глубины кодирования
- количества каналов
- частоты дискретизации
Задание 2.
Что означает формулировка “запись в формате квадро”?
- При записи использовалась глубина кодирования 4 бит
- Частота дискретизации равна 2 Гц
- Количество каналов записи равно 2
- Количество каналов записи равно 4
Задание 3.
В студии звукозаписи производится одноканальная (моно) запись длиной 3 минуты 25 секунд и с частотой дискретизации 35 кГц. Определите и запишите в ответ максимальную битовую глубину, которая может быть использована при записи музыкального фрагмента, если объём файла не превышает 30 Мбайт.
- 35
- 36
- 70
- 140
Задание 4.
Для записи песни использовалась четырехканальная (квадро) аудиодорожка. Ее сохранили на компьютер, с объемом 10 Мбайт. Тот же файл был записан еще раз в формате двухканальной (стерео) записи с разрешением в 3 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Определите количество мегабайт, которое занимает файл при повторной записи.
- 5
- 8
- 20
- 10
Ответы: 1. — 2; 2. — 4; 3. — 1; 4. — 4.
Определение объёма памяти, необходимого для хранения графической информации
Различают три вида компьютерной графики:
- растровая графика;
- векторная графика;
- фрактальная графика.
Они различаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге. Наименьшим элементом растрового изображения является точка (пиксель), векторное изображение строится из геометрических примитивов, фрактальная графика задаётся математическими уравнениями.
Расчёт информационного объёма растрового графического изображения основан на подсчёте количества пикселей в этом изображении и на определении глубины цвета (информационного веса одного пикселя).
Глубина цвета зависит от количества цветов в палитре:
N=2i
.
(N) — это количество цветов в палитре,
(i) — глубина цвета (или информационный вес одной точки, измеряется в битах).
Чтобы найти информационный объём растрового графического изображения (I) (измеряется в битах), воспользуемся формулой
I=i⋅k
.
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит).
Пример:
Полина увлекается компьютерной графикой. Для конкурса она создала рисунок размером (1024*768) пикселей, на диске он занял (900) Кбайт. Найди максимально возможное количество цветов в палитре изображения.
Дано
(k=1024*768);
(I=900) Кбайт.
Найти: (N).
Решение
Чтобы найти (N), необходимо знать (i):
N=2i
.
Из формулы
I=i⋅k
выразим
i=Ik
, подставим числовые значения. Не забудем перевести (I) в биты.
Получим
i=900∗1024∗81024∗768≈9,3
.
Возьмём (i=9) битам. Обрати внимание, нельзя взять (i=10) битам, так как в этом случае объём файла (I) превысит (900) Кбайт. Тогда
N=29=512.
Ответ: (512) цветов.
На качество изображения влияет также разрешение монитора, сканера или принтера.
Разрешение — величина, определяющая количество точек растрового изображения на единицу длины.
Получается, если увеличить разрешение в (3) раза, то увеличится в (3) раза количество пикселей по горизонтали и увеличится в (3) раза количество пикселей по вертикали, т. е. количество пикселей в изображении увеличится в (9) раз.
Параметры PPI и DPI определяют разрешение или чёткость изображения, но каждый относится к отдельным носителям:
• цифровой (монитор) — PPI;
• печать (бумага) — DPI.
При решении задач величины PPI и DPI имеют одинаковый смысл.
При расчётах используется формула
I=k⋅i⋅ppi2
.
(I) — это информационный объём растрового графического изображения (бит);
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит),
ppi (или dpi) — разрешение.
Пример:
для обучения нейросети распознаванию изображений фотографии сканируются с разрешением (600) ppi и цветовой системой, содержащей (16 777 216) цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет (18) Мбайт. В целях экономии было решено перейти на разрешение (300) ppi и цветовую систему, содержащую (65 536) цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Решение
Заметим, что
16777216=224
, значит,
i1=24
бита.
, значит,
i2=16
бит.
Воспользуемся формулой
I=k⋅i⋅ppi2
.
I1=24⋅k⋅6002;I2=16⋅k⋅3002;I1I2=24⋅k⋅600216⋅k⋅3002=6;18I2=6;I2=186=3.
Ответ: (3) Мбайта.
Определение объёма памяти, необходимого для хранения звуковой информации
Звук — это распространяющиеся в воздухе, воде или другой среде волны с непрерывно меняющейся амплитудой и частотой.
Чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму. Для этого его подвергают временной дискретизации и квантованию: параметры звукового сигнала измеряются не непрерывно, а через определённые промежутки времени (временная дискретизация); результаты измерений записываются в цифровом виде с ограниченной точностью (квантование).
Сущность временной дискретизации заключается в том, что через равные промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации.
Частота дискретизации ((H)) — это количество измерений громкости звука за одну секунду.
Частота дискретизации измеряется в герцах (Гц) и килогерцах (кГц). (1) кГц (=) (1000) Гц. Частота дискретизации, равная (100) Гц, означает, что за одну секунду проводилось (100) измерений громкости звука.
Качество звукозаписи зависит не только от частоты дискретизации, но также и от глубины кодирования звука.
Глубина кодирования звука или разрешение ((i)) — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.
В результате измерений звукового сигнала будет получено некоторое значение громкости, при этом все результаты измерений будут лежать в некотором диапазоне — количество уровней дискретизации.
Обозначим за (N) количество уровней дискретизации, тогда глубину кодирования можно найти по формуле:
N=2i
.
Для решения задач на нахождение объёма памяти, необходимого для хранения звуковой информации, воспользуемся формулой:
I=H⋅i⋅t⋅k
, где
(I) — информационный объём звукового файла (бит);
(H) — частота дискретизации (Гц);
(i) — глубина кодирования информации (бит);
(k) — количество каналов (моно — (1) канал, стерео — (2) канала, квадро — (4) канала).
Пример:
для распределения птиц по категориям обучают нейросеть. Для этого загружают звуки, издаваемые птицами. Каждый файл записан в формате монозвукозаписи с частотой дискретизации (128) Гц. При записи используется (64) уровня дискретизации. Запись длится (6) минут (24) секунды. Определи размер загружаемого файла в килобайтах.
Дано
(k=1);
(H=128) Гц;
(N=64);
(t=384) секунды.
Найти: (I) (Кбайт).
Решение
Воспользуемся формулой
N=2i
, (i=6) бит.
Подставим числовые значения в формулу
I=H⋅i⋅t⋅k
и переведём биты в килобайты:
Ответ: (36) килобайт.
Любой файл может быть передан по каналу связи, тогда объём переданной информации вычисляется по формуле:
I=V⋅t
, где
(I) — объём информации (бит);
(V) — пропускная способность канала связи (бит/секунду);
(t) — время передачи (секунды).
Пример:
в дельте Волги орнитологи оцифровывают звуки птиц и записывают их в виде файлов без использования сжатия данных. Получившийся файл передают в Астраханский биосферный заповедник по каналу связи за (56) секунд. Затем тот же файл оцифровывают повторно с разрешением в (8) раз ниже и частотой дискретизации в (3) раза выше, чем в первый раз. Сжатие данных не производится. Полученный файл передают в Кавказский природный заповедник; пропускная способность канала связи с Кавказским заповедником в (2) раза ниже, чем канала связи с Астраханским заповедником. Сколько секунд длилась передача файла в Кавказский заповедник?
Решение
Воспользуемся формулой
I=H⋅i⋅t⋅k
.
I1=k⋅i⋅t⋅H;I2=k⋅i8⋅t⋅3⋅H;I2I1=38.По условиюV2=V12.
Выразим (V) из формулы
I=V⋅t
, получим
V=It
, учтём, что
t1=56 секунд.Тогда I2t2=I156⋅2;t2=56⋅2⋅I2I1=56⋅2⋅38=42.
Ответ: (42) секунды.
Обрати внимание!
1 Мбайт=220 байт=223 бит.1 Кбайт=210 байт=213 бит.
Система задач на кодирование звуковой информации
При решении задач данной группы учащиеся должны опираться на следующие понятия:
Глубина звука (глубина кодирования)- количество бит на кодировку звука.
Уровни громкости (уровни сигнала, уровни квантования, уровней дискретизации) – звук может иметь разные уровни громкости. Количество различных уровней громкости рассчитывается по формуле N=2i— где i- глубина звука.
Временная дискретизация – процесс разбиения звуковой волны на отдельные маленькие временные участки во время кодирования непрерывного звукового сигнала. Для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук.
Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1секунду). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измеряется в герцах (Гц).
Качество двоичного кодирования – величина, которая определяется глубиной кодирования и частотой дискретизации.
Общая формула вычисления информационного объема звукового файла.
V=Сh×ν×t×i, где
Сh- количество каналов (обычно 1(моно), 2(стерео), 4(квадро)),
ν- частота дискретизации в герцах, t- время звучания / звукозаписи в секундах,
i- число бит разрешения (разрядность регистра)
V – объем памяти для хранения звукового фрагмента в байтах.
Аудиоадаптер (звуковая плата) – устройство, преобразующее электрические колебания звуковой частоты в числовой двоичный код при вводе звука и из числового кода в электрические колебания при воспроизведении звука.
Характеристики аудиоадаптера – частота дискретизации и разрядность регистра.
Разрядность регистра — число бит в регистре аудиоадаптере. Чем больше разрядность тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2i=N различных значений.
Решение задач на кодирование звуковой информации
Задача 1. Производится четырех канальная (квадро) звукозапись с частой дискретизации 32кГц и 16 битным разрешением. Запись длится две минуты, ее результаты записываются в файл, сжатие данных не производится. Каков размер полученного звукового файла?
Решение. Воспользуемся формулой вычисления информационного объема звукового файла. V=Сh×ν×t×i.
Из условия задачи имеем: Сh=4 (квадро запись).
Частота дискретизации ν=32кГц=32000Гц, т.к. 1кГц=1000Гц .
Время записи t=2мин=120сек.
Число бит разрешения i= 16 бит.
Подставим данные задачи в формулу. V=4×32000×120×16=245760000бит=30720000байт=30000Кбайт=29,3Мбайт
245760000бит:8=30720000байт
30720000байт:1024=30000Кбайт
30000Кбайт:1024≈29,3Мбайт
Ответ: размер полученного звукового файла равен 29,3Мбайт
Задача 2. Записанный звуковой файл занимает на диске 5,25Мбайт. Разрядность звуковой платы — 16бит. Какова длительность звучания звукового аудиофайла, записанного с частотой дискретизации 22,05 кГц.
Решение. Выведем из формулы вычисления объема звукового файла время звучания аудиофайла.
V=Сh×ν×t×i,
Из условия задачи имеем:
Размер звукового файла V=5,25Мбайт=550524байт
Количество каналов Сh=1, так это обычный аудиофайл.
Частота дискретизации ν=22,05кГц=22050Гц.
Разрядность i=16бит=2байт.
Подставим данные задачи в формулу нахождения времени.
Ответ: время звучания данного звукового файла 124,8с.
Задача 3. Одна минута записи цифрового стерео аудиофайла занимает на диске 2,6 Мбайт, разрядность звуковой платы -16 бит. С какой частотой дискретизации записан звук? Решение. Выведем из формулы вычисления объема звукового файла частоту дискретизации .
V=Сh×ν×t×i,
Из условия задачи имеем:
Размер звукового файла V=2,6Мбайт=2726297,6байт
Количество каналов Сh=2, так это стерео аудиофайл (двухканальный).
Разрядность i=16бит=2байт.
Время звучания t=1мин=60сек.
Подставим данные значения в формулу нахождения частоты дискретизации.
Ответ: звук записан с частотой дискретизации 11,3кГц
Задача 4. Производится одноканальная (моно) звукозапись с частотой дискретизации 256 Гц. При записи использовались 128 уровней дискретизации. Запись длится 8 минут, её результаты записываются в файл, причём каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Каков размер полученного файла?
Решение. Воспользуемся общей формулой вычисления размера звукового файла. V=Сh×ν×t×i.
Из условия задачи имеем:
Количество каналов Сh =1 так производится одноканальная звукозапись.
Частота дискретизации ν =256Гц.
Время записи 8 мин=480сек.
При записи использовалось N= 128 уровней дискретизации.
Число бит разрешения (i) вычислим по формуле N=2i. 2i=128, 27=128, i=7бит.
Подставив данные задачи в формулу V=Сh×ν×t×i получим:
V=1×256×480×7=860160бит=107520байт=105Кбайт
Ответ. Размер файла 105Кбайт
Задача 5. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 50 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 5 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 6 раз выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.
Решение. Обозначим первоначальный объем музыкального фрагмента записанного в виде файла через V1=Х.
Далее файл был передан в город А по каналу связи за 50 сек., тогда скорость передачи данного файла υ1=Х/50.
Так как после передачи звуковой файл был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 5 раз меньше, чем в первый раз. Тогда объем полученного файла будет равен: V2=3/5X .
После файл объемом V2=3/5X, был передан в город Б по каналам связи с пропускной способностью в 6 раз выше, чем с канала связи с городом А, следовательно скорость передачи будет равна:
Вычислим сколько секунд длилась передача файла в город Б по формуле ,
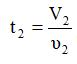
Ответ: 5сек. длилась передача звукового файла из города А в город Б.
Задачи для самостоятельного решения