Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
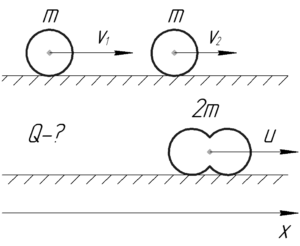
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
габбас
[215K]
5 месяцев назад
По закону сохранения энергии найдем скорость шаров после соударения. m1*v1-m2*v2=(m1+m2)*v, v=(m1*v1-m2*v2)/(m1+m2). v = (2*4-3*2)/(2+3)=2/5=0,4 м/с.
Теперь по закону сохранения энергии можно найти количество теплоты, которая выделяется при соударении шаров. Q=(m1*v1^2)/2 + (m2*v2^2)/2 — (m1+m2)*v^2)/2. Q = (2*4^2)/2 + (3*2^2)/2 — ((2+3)*0,4^2)/2 = 16 + 6 — 0,4=22-0,4=21,6. Ответ: 21,6 Дж.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
2014-05-31
Какое количество тепла выделится при лобовом ударе двух свинцовых шаров массой m = 1 кг каждый, скользящих без вращении на абсолютно гладкой горизонтальной поверхности по одной прямой в одном направлении? Скорость первого шара $v_{1}=10 см/с$, скорость второго $v_{2} = 20 см/с$. Удар шаров считать абсолютно неупругим
Решение:
Так как удар абсолютно неупругий, то после удара оба шара будут двигаться с одинаковой скоростью $v$. Согласно закону сохранения импульса
$mv_{1}+mv_{2}=2mu$.
Отсюда
$v=frac{v_{1}+v_{2}}{2}$.
До столкновения шары обладали кинетической энергией
$W_{1}=frac{mv_{1}^{2}}{2}+frac{mv_{2}^{2}}{2}$.
После удара их кинетическая энергия равна
$W_{2}=2 frac{mv^{2}}{2}= frac{m(v_{1}+v_{2})^{2}}{4}$.
В результате удара кинетическая энергия системы уменьшается на величину
$Delta = W_{1} – W_{2}=frac{m}{4}(v_{1}-v_{2})^{2} = 0,0025 Дж$.
Эта энергия и переходит в тепло.
При неупругом ударе выделяется количество теплоты, равное
Q = W0 – W.
Найдем энергии W0 и W. За нулевую высоту примем высоту поверхности, по которой двигается брусок.
По условию массы тел равны (два одинаковых тела) и равны начальные скорости υ1 = υ2.
Полная механическая энергия тел в начальном состоянии
[ W_{0} =frac{mcdot upsilon _{1}^{2} }{2} +frac{mcdot upsilon _{2}^{2} }{2} =mcdot upsilon _{1}^{2}. ]
Полная механическая энергия тел в конечном состоянии
[ W=frac{2mcdot upsilon ^{2} }{2} =mcdot upsilon ^{2}, ;;; (1) ]
где υ — скорость тел после столкновения.
Так как удар неупругий, то выполняется закон сохранения импульса. Воспользуемся им для нахождения скорости υ тел после столкновения (рис. 1):
[ mcdot vec{upsilon }_1 +mcdot vec{upsilon }_2 =2mcdot vec{upsilon }, ]
0Х: m⋅υ1 = 2m⋅υх, 0Y: m⋅υ2 = 2m⋅υy.
Тогда
[ upsilon^{2} =upsilon _{x}^{2} +upsilon _{y}^{2} =left(frac{upsilon _{1} }{2} right)^{2} +left(frac{upsilon _{2} }{2} right)^{2} =frac{upsilon _{1}^{2} }{2}. ]
После подстановки в уравнение (1) получаем
[ W=frac{mcdot upsilon _{1}^{2} }{2}. ]
Количество теплоты, которое выделится при неупругом ударе шаров, будет равно
[ Q=mcdot upsilon _{1}^{2} -frac{mcdot upsilon _{1}^{2} }{2} =frac{mcdot upsilon _{1}^{2} }{2}. ]
Часть кинетической энергии, которая переходит во внутреннюю энергию, равна
[ frac{Q}{W_{0} } cdot 100% =frac{mcdot upsilon _{1}^{2} }{2mcdot upsilon _{1}^{2} } cdot 100% =50%. ]
Введение
Определение. Центральный удар — это соударение двух тел , при котором скорости каждого из тел направлены вдоль линии, соединяющей центры обоих тел.
Замечание. Если один из шаров покоится, то скорость второго тела должна быть направлена вдоль линии соединяющей центры тел.
При решении задач на столкновение двух и более тел надо привыкнуть к следующим формулировкам:
- Абсолютно упругий удар (упругий удар) — это тип соударения, при котором выполняется закон сохранения энергии и закон сохранения импульса. Часто этот тип соударения применим к железным шарикам.
- Неупругий удар — это удар, при котором выполняется закон сохранения импульса и закон изменения механической энергии (так как теряется часть энергии при ударе).
- Абсолютно неупругий удар — это удар, при котором два тела продолжают двигаться как единое целое. При этом столкновении выполняется закон сохранения импульса и закон изменения механической энергии.
Замечание. Как мы видим, для решения задач нужно сначала записать соответствующие законы сохранения (энергии и импульса) или изменения энергии. Далее необходимо решить получившуюся систему уравнений.
Задача 2
На бетонную сваю массой M = 9 т падает бетонная плита массой m = 1 т с высоты H = 10 м. Найти, на какое расстояние погрузится свая, если сила сопротивления грунта F = 1000 кН.
Решение. В этой задаче необходимо учесть, что при ударе бетонной плиты на сваю удар будет абсолютно неупругий, следовательно, часть энергии потеряется.
Найдем скорость плиты v на момент соударения со сваей.
ЗСЭ:

Далее задача повторяет предыдущую, поэтому воспользуемся ее результатом для конечной скорости (V) после соударения (считаем, что время удара очень мало, поэтому грунт не оказывает никакого влияния).

Из теоремы об изменении кинетической энергии следует, что работа силы трения равна изменению кинетической энергии (3).

где S — расстояние, на которое опустилась свая, f — сила сопротивления грунта с учетом веса сваи и плиты.

Подставив все выражения в исходную формулу (3). получим:

Ответ: 11 мм.
Замечание. Если F ≤ (m + M)g, то иногда можно пренебречь последним выражением (m + M)g.
Пример 3
Подробно рассматривать общий случай упругого удара для двух шаров мы не будем ввиду громоздкости вычислений. Запишем только законы сохранения и некоторые частные случаи.
Условие задачи можно увидеть на рисунке 2:

Решение:
ЗСИ:
ОХ:

ЗСЭ:


Решая соответствующую систему уравнений, можно найти конечные скорости шаров. Решить систему уравнений в таком виде затруднительно, поэтому легче рассматривать случай, когда шар массой M покоится. Решив этот случай, можно сделать интересные выводы:
- Если m = M, то шары обменяются скоростями.
2. Если m < M, то шарик с массой m поменяет направление, а шар M будет двигаться вправо.
3. Если m > M, то шарик массой m и M будет двигаться вправо.
Замечание. В этой задаче первоначальный выбор для направления конечных скоростей не важен. Если истинная скорость направлена в другую сторону, то в ответе мы получим знак минус.
Переход в систему отсчета, связанную с центром масс
Иногда в задачах выгодней переходить в систему отсчета, связанную с центром масс. В этой системе отсчета импульс системы равен нулю (так как импульс любой системы равен импульсу центра масс). Для перехода в систему отсчета, связанную с центром масс, необходимо найти скорость центра масс и вычесть ее (векторно) из скорости каждого тела системы.

В системе центра масс можно также можно пользоваться законом сохранения/ изменения энергии.
Для примера рассмотрим нашу первую задачу:
Железный шар массы m = 500 г движется по гладкой горизонтальной поверхности со скоростью 10 м/с и сталкивается с неподвижным восковым шаром, имеющим массу М = 200 г, после чего оба шара движутся вместе. Найдите количество теплоты, выделившееся при ударе.
Решение:
Найдем скорость центра масс:

В системе отсчета, связанной с центром масс. конечная энергия равна 0.
Начальная скорость железного шара в системе отсчета, связанной с центром масс:

Запишем закон сохранения энергии:

(конечная энергия равна нулю).
Подставив все в энергию, получим:

Ответ: 7,14 Дж.
Нецентральный удар
Задача 4
Первый шар движется со скоростью v и налетает на такой же покоящийся шар. Найти угол, под которым разлетятся два этих шарика в результате нецентрального абсолютно упругого удара (под углом β). См. рисунок 3.

Эту задачу бессмысленно решать традиционными способами, записывая закон сохранения и энергии и импульса на определенные оси.
Запишем ЗСИ в векторном виде и ЗСЭ:

Тогда получим:

Из двух последних выражений видно, что векторы скоростей образуют прямоугольный треугольник. Следовательно, в независимости от угла β и начальной скорости шара шары разлетятся под прямым углом.
Ответ: 90 градусов.
Список литературы:
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
- Козел С. М., Слободянин В. П. Всероссийские олимпиады по физике 1992–2001. М., 2002
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Вопросы к статье
- Можно ли использовать закон сохранения импульса и энергии в задачах о неупругом столкновении тел, движущихся по горизонтальной плоскости?
а) Импульс и энергия не сохраняются.
б) Импульс сохраняется, энергия — нет.
в) Импульс и энергия сохраняются.
г) Энергия сохраняется, импульс — нет.
Комментарии к неправильным вариантам:
Закон сохранения энергии выполняется, так как нет диссипативных сил. Закон сохранения импульса выполняется вдоль проекции на некоторую ось (см. замечание 2, пункты 1 и 2).
2. Импульс системы материальных точек сохраняется, если:
а) Нет внешних сил или они не совершают работу.
Комментарий: сила может не совершать работу, но изменять направление импульса (например, сила Лоренца).
б) На материальные точки не должны действовать никакие силы.
Комментарий: если силы внутренние, то они не изменяют импульс системы.
в) Нет внешних сил, или они взаимно скомпенсированы.
