Расчет необходимого количества респондентов
Необходимое количество респондентов зависит от целей опроса и того, насколько важна достоверность результатов. Чем выше достоверность Вы хотите получить, тем ниже должен быть допустимый предел погрешности.
Определения
Чтобы рассчитать размер выборки, необходимо знать следующую информацию:
Расчет размера выборки
Вы можете за несколько секунд рассчитать необходимое количество респондентов с помощью нашего калькулятора для расчета размера выборки. Чтобы рассчитать размер выборки вручную, используйте следующую формулу:
Рекомендованные размеры выборки
Ниже приведена таблица, в которой указаны рекомендованные значения численности генеральной совокупности для предела погрешности при уровне доверия 95%. Мы рассчитали рекомендованные размеры выборки по указанной выше формуле. В некоторых случаях размеры выборки были округлены вверх до 5 или 10. Для более точного расчета используйте наш калькулятор размера выборки.
Пример объема выборки
Вы отправляете родителям детей Вашей школы опрос с вопросом о том, поддерживают ли они продление учебного дня. Вопрос имеет варианты ответа «Да» и «Нет».
Общее количество родителей (численность совокупности) — 10 000, и Вас устраивает предел погрешности ±10%. По таблице выше Вы можете определить, что в опросе должно принять участие не менее 100 человек.
70% из 100 опрошенных родителей ответили, что согласны на продление учебного дня. Таким образом, можно предположить, что если бы в опросе участвовали все 10 000 родителей, 60-80% людей поддержало бы продление учебного дня.
Сколько людей следует попросить пройти опрос?
Процентная доля ответивших может определять, какому количеству людей нужно отправить опрос. Чем выше процентная доля ответивших, тем меньше людей необходимо попросить пройти опрос.
Например, если Вам нужно 100 респондентов и Вы ожидаете, что 25% людей, приглашенных принять участие в опросе, ответят на него, Вам необходимо пригласить 400 человек.
По следующей формуле можно рассчитать, какое количество людей необходимо пригласить для участия в опросе, на основе ожидаемой процентной доли ответивших:
Необходимое количество респондентов
Определите количество людей, которые должны ответить на ваш опрос.
÷ Процентная доля ответивших
Разделите на ожидаемую процентную долю ответивших (используйте «25» вместо 25 %; если используете «.25», пропустите этап 3).
Затем умножьте на 100 (если на этапе 2 были введены процентные значения, а не десятичные дроби).
Похожие статьи
Как определить количество участников опроса и быть уверенным, что результат обработки анкет будет достоверным?
Часто для проведения маркетинговых исследований и принятия управленческих решений мы опираемся на всевозможные опросы респондентов, при этом получить обратную связь от всех представителей нужной нам группы не представляется возможным или экономически нецелесообразно. Но как понять, будет ли мнение определенного количества опрошенных представлять всю изучаемую группу?
Такие задачи легко решаются при помощи выборочных наблюдений, при которых обследованию подвергается часть представителей совокупности (группы), а результаты обследования распространяются на все изучаемое явление. В зависимости от исходных данных нам приходится решать одну из задач:
- Какое минимальное или оптимальное количество респондентов необходимо привлечь для участия в опросе?
- Будет ли результат достоверным при заранее известном количестве участников?
Например, Вы провели выставку «Товары для дома и сада» и необходимо получить обратную связь от посетителей мероприятия. Количество посетителей выставки составило 15 000 чел.
Для решения первой задачи вам необходимо знать, сколько минимум анкет обратной связи необходимо собрать по результату опроса посетителей из общего числа 15 000 чел.
Вторая задача возникает в том случае, если вы уже имеете какое-то количество заполненных анкет (например, 650) и хотите убедиться, можно ли распространить выводы на всю изучаемую группу.
Для начала предлагаю определиться с терминологией.
Генеральная совокупность — это суммарная численность объектов наблюдения (в нашем примере это все участники выставки, 15000 чел.), обладающих определенным набором признаков, ограниченная в пространстве и времени.
Выборка или выборочная совокупность — часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. В нашем примере для Задачи 1 – это как раз искомая величина, а для Задачи 2 – 650 чел.
Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки — свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.
В нашем примере выборка, целиком состоящая из посетителей, владеющих дачей или садом, не будет репрезентировать всех посетителей выставки, также как и выборка из посетителей, живущих в многоквартирных домах, т.е. в опросе должны участвовать посетители разных категорий.
Ошибка выборки или доверительный интервал является показателем погрешности измерений. Это отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности. Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не более 5%.
Доверительный уровень или точность – интервал, в котором с той или иной вероятностью находится генеральный параметр. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95 (95%).
Применить все эти показатели и получить необходимые результаты можно в расчетах при помощи достаточно сложных статистических формул, табулированных значений в Excel или воспользоваться онлайн-сервисом расчета.
Мы выполнили такие расчеты для нашего примера и вот что получилось.
Задача 1. От какого количества участников выставки (напомним, всего 15 000 чел.) необходимо получить обратную связь, если мы принимаем ошибку выборки на уровне 5%, а доверительный уровень соответствует рекомендованному 95%?
Ответ – 375 человек. Т.е. получив 375 анкет обратной связи мы сможем смело распространить результаты опроса на всю генеральную совокупность с погрешностью 5%.
Задача 2. У нас есть 650 анкет обратной связи участников выставки. Достаточно этого количества и какова при этом ошибка выборки?
Ответ – 650 анкет будет достаточно для распространения результата опроса на всю генеральную совокупность с погрешностью 3,76% (ниже максимально рекомендованного 5%) с уровнем доверия 95%.
Какие именно алгоритмы, сервисы и формулы применяются для расчетов мы обязательно расскажем в наших следующих публикациях.
Создать онлайн опрос
Другие статьи:
- Как найти респондентов для онлайн опроса
- Респонденты для опроса
- Индекс удовлетворенности клиентов CSI
- Конструктор опросов онлайн
Итак, вы посчитали, сколько человек выбрали тот или иной вариант ответа в вопросе анкеты.
Теперь чтобы выразить всё это в процентах нужно использовать такую формулу:
номер варианта (%) = (кол-во человек, выбравших этот вариант / общее число респондентов) * 100%.
При этом после деления может получиться бесконечная десятичная дробь — в таком случае в ней нужно оставить 2 знака после запятой.
Когда таких бесконечных дробей несколько, и потом в итоге сумма получается не 100%, а 99,9%, то одну из дробей просто округляем в большую сторону (к примеру, вместо 13,33 берём 13,34) и всё.
Пример.
Всего респондентов: 40 человек.
За первый вариант проголосовало 19 человек, за второй — 5 человек, за третий — 6 человек, за четвёртый — 10 человек.
Получим следующее:
Первый вариант: (19 / 40) * 100% = 0,475 * 100% = 47,5%.
Второй вариант: (5 / 40) * 100% = 0,125 * 100% = 12,5%.
Третий вариант: (6 / 40) * 100% = 0,15 * 100% = 15%.
Четвёртый вариант: (10 / 40) * 100% = 0,25 * 100% = 25%.
Проверяем: 47,5% + 12,5% + 15% + 25% = 100%.
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
В каждой профессии есть свой набор любимых вопросов. Для исследователей рынка этот список возглавляет, безусловно, вопрос о размере выборки. Обычно его формулируют так:
- Мы хотели бы заказать исследование по посетителям московских торговых центров. Какая нам нужна выборка?
- Наша целевая аудитория – примерно 300 000 человек. Сколько людей нам нужно опросить, чтобы было репрезентативно? А если целевая аудитория будет 3 млн?
- Нам нужно оценить потенциал продаж квартир в Санкт-Петербурге жителям северных городов России. Какую сделать выборку?
Размер выборки действительно важен, потому что определяет стоимость будущего исследования, не говоря уже о качестве итоговых результатов и выводов. В этой статье мы расскажем о том, как рассчитать оптимальный размер выборки массового опроса. Наш материал будет полезен всем, кто так или иначе сталкивается с необходимостью проведения маркетинговых исследований своими силами или заказывает их у специализированного агентства.
Главное заблуждение о размере выборки
Многие уверены, что чем больше размер целевой группы, тем больше должен быть размер выборки. Поэтому, якобы, чтобы узнать мнение жителей маленького города, достаточно опросить человек 200-300, ну а для выяснения мнения по России в целом и 5000 будет мало.
Между тем, этот стереотип не имеет ничего общего с реальностью. Размер выборки не зависит от численности целевой группы (на языке статистики она называется «генеральной совокупностью») и определяется двумя совершенно другими факторами. Единственное исключение из этого правила – случаи, когда генеральная совокупность очень маленькая, например, 1-2 тысячи человек, но такие ситуации в реальной практике маркетинговых исследований встречаются редко.
Два фактора, от которых зависит размер выборки
Размер выборки массового опроса зависит от двух факторов:
- Точности данных, которые нужно получить на выходе – это та самая «статистическая погрешность». Для выборки в 100 респондентов она будет в пределах плюс-минус 10%, а для выборки в 1000 респондентов – в пределах плюс-минус 3,1%. Более подробно об этом – ниже.
- Количества и размера подгрупп, на которые нужно разбивать выборку при анализе. Например, если проводится электоральное исследование, то в основном нас будет интересовать ядро активных избирателей. Как правило, доля «ядра» редко превышает 20-25% от всего населения. Поэтому размер выборки нужно рассчитывать так, чтобы одна четверть от ее общего объема позволяла проводить полноценный статистический анализ.
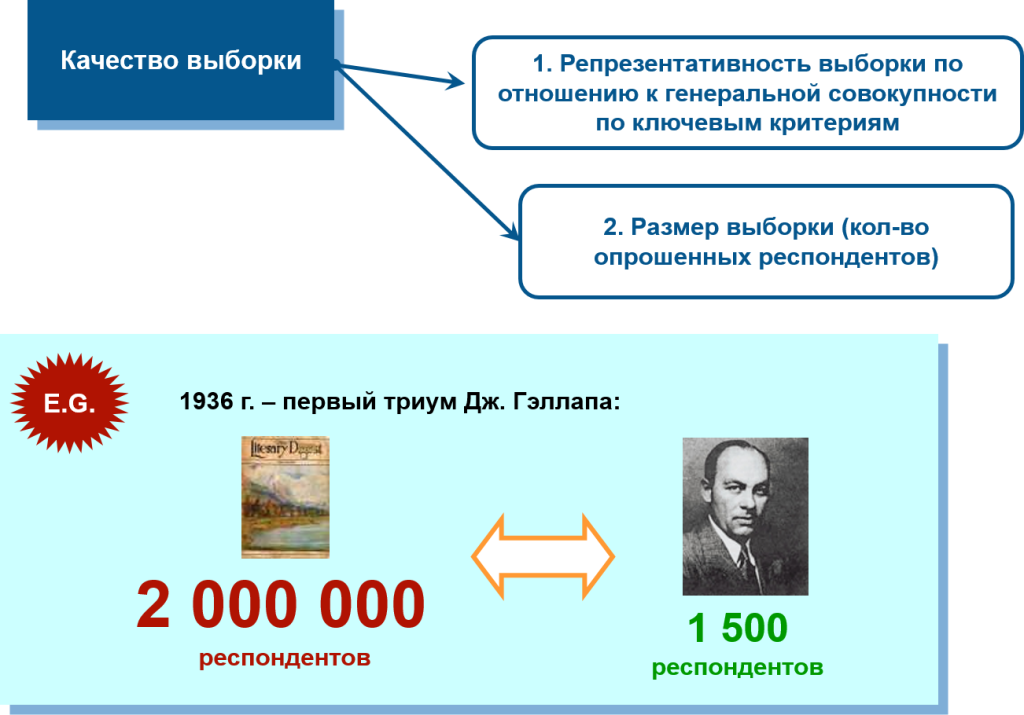
Вопреки расхожему мнению, качество выборки определяется не ее размером, а репрезентативностью. Репрезентативность – это соответствие между выборкой и генеральной совокупности по ключевым параметрам. Чаще всего, в качестве таких «реперных точек» используют легко измеряемые социально-демографические показатели: пол, возраст, образование, род занятий и место жительства.
Две разновидности ошибки выборки
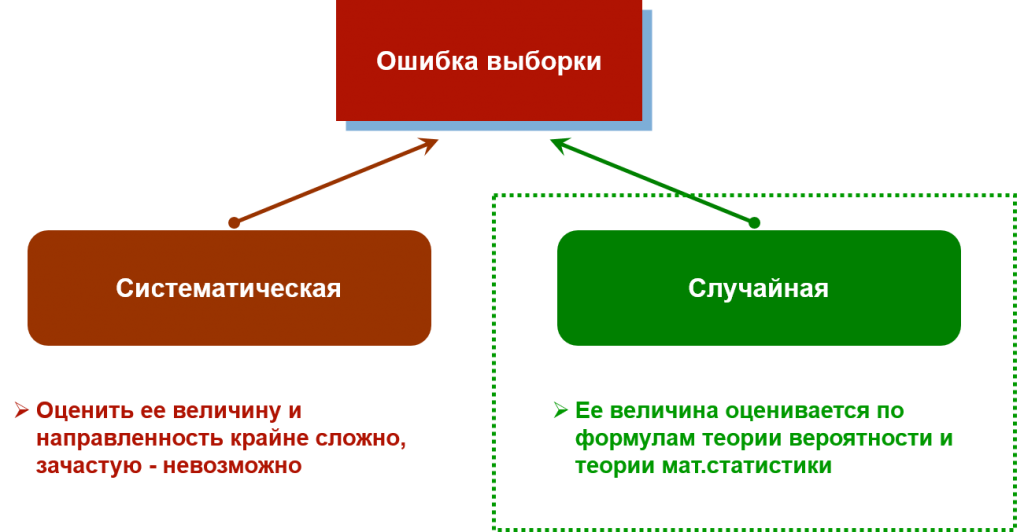
Любое выборочное наблюдение (то есть когда мы опрашиваем не всех подряд, а делаем случайный отбор из генеральной совокупности) сопряжено с погрешностью данных. Эту погрешность обычно называют «ошибкой выборки». Она может быть двух видов:
- Систематическая – связана с ошибками проектирования выборки. Оценить ее размер, направление и степень смещения очень сложно, чаще всего – невозможно. Например, если вопросы респондентам будут задавать представители маргинальных социальных слоев, это повлияет на готовность участвовать в исследовании со стороны представителей более обеспеченных групп населения. В итоге это приведет к крайне трудно оцениваемой систематической ошибке и искажению данных.
- Случайная – связана с действием законов статистики. Ее размер легко рассчитывается по формулам математической статистики и теории вероятности. Они позволяют делать обоснованные выводы о доверительном интервале признака. Например, если статистическая погрешность составляет плюс-минус 10%, а полученное значение показателя оказалось равно 25%, то доверительный интервал равен от 15% до 35%.
Задача исследователя – собрать данные так, чтобы минимизировать систематическую ошибку выборки. Тогда можно будет свести статпогрешность лишь к случайной ошибке, которую можно рассчитать по формулам.
Как рассчитать размер случайной ошибки выборки
Случайная ошибка выборки зависит не только от объема выборки, но и от дисперсии, то есть степени однородности данных. Чем однороднее данные (т.е. чем меньше разброс полученных значений, или дисперсия), тем меньше ошибка выборки.
Существует формула расчета случайной ошибки выборки, однако для удобства рекомендуем пользоваться онлайн-калькуляторами, например, вот этим. Он позволяет легко провести два вида расчета:
- рассчитать величину статистической погрешности на основе размера выборки и предполагаемой дисперсии;
- определить размер выборки, требуемый для получения оценки нужной степени точности.
Вот так выглядит его рабочее окно:
В качестве параметра доверительной надежности (одно из полей в калькуляторе) обычно используется значение в 95%. Это означает, что в 95% случаев распределение признака в генеральной совокупности попадет в рассчитанный доверительный интервал (т.е. само значение признака в выборке плюс-минус размер статистической погрешности). Реже используется значение надежности в 97% или 99% – оно, соответственно, означает, что подобное попадание произойдет в 97% или 99% случаев. В данном случае надежность выборки повышается, но увеличивается размер выборки.
Самое сложное при определении размера выборки – поиск компромисса между требуемой точностью и стоимостью сбора данных. Этот процесс усложняется тем, что увеличение размера выборки в четыре раза приводит к увеличению точности лишь в два раза (соответствует квадратному корню от величины прироста выборки).
Кейс: определение размера выборки для оценки потенциала рынка продаж столичной недвижимости покупателям из регионов
В ноябре-декабре 2016 года мы провели исследование спроса на квартиры в новостройках Москвы и Санкт-Петербурга со стороны жителей разных городов России. Исследование включало в себя три метода сбора данных: массовый репрезентативный опрос населения в возрасте от 20 до 60 лет (проводился с использованием технологии CATI), а также серию экспертных интервью с риэлторами и глубинных интервью с потенциальными покупателями квартир.
Исследование охватывало 33 города, отличающихся повышенным спросом на петербургскую и московскую недвижимость. Плановая выборка исследования, рассчитанная по формулам, составила 21 500 респондентов. Этот объем значительно больше «стандартного» объема выборки, используемого в маркетинговых исследованиях. С чем же связан такой большой размер выборки?
Все дело в том, что клиенту были нужны оценки отдельно по каждому городу, а не просто «в целом по стране». Фактически мы работаем не с 1 выборкой, а с 33 отдельными выборками по каждому городу. Доля людей, заинтересованных в покупке квартиры в Санкт-Петербурге или Москве, была экспертно определена в рамках 5% от числа жителей опрашиваемых городов.
В зависимости от важности города для заказчика, руководитель проекта со стороны Агентства определил допустимую статистическую погрешность, в которую должны укладываться итоговые результаты. Для этого мы использовали специальный макрос в MS Excel, но эти расчеты можно также выполнить с помощью калькулятора выборки. В результате размер выборки варьировал от 500 до 1000 респондентов по каждому из городов исследования, что в сумме и дало заявленные 21 500 человек.
Резюме
Чтобы рассчитать выборку маркетингового исследования, используйте следующий алгоритм:
- Определите структуру целевой группы. Планируете ли вы анализировать отдельные подгруппы или достаточно будет анализа по выборке в целом?
- Определите желаемую точность данных. Например, если нужно оценить динамику рыночной доли за год, подставьте в специальный калькулятор примерное значение доли и «поиграйте» с разными объемами выборки.
- Найдите баланс между стоимостью сбора данных (прямо пропорциональна объему выборки) и требуемой точностью.