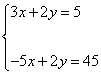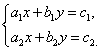Предположим, требуется найти все пары значений переменных х и у, которые удовлетворяют уравнение
ху – 6 = 0 и уравнение у – х – 1 = 0, то есть необходимо найти пересечение множеств решений этих уравнений. В таких случаях говорят, что надо решить систему уравнений ху – 6 = 0 и у – х – 1 = 0.

{ху – 6 = 0,
{у – х – 1 = 0.
Пара значений переменных, обращающая в истинное равенство каждое уравнение системы, называется решением системы уравнений с двумя переменными.
Решить систему уравнений – значит найти множество её решений.
Рассмотрим системы двух линейных уравнений с двумя переменными, в которых в каждом уравнении хотя бы один из коэффициентов отличен от нуля.
Графическое решение систем такого вида сводится к отысканию координат общих точек двух прямых.
Как известно, две прямые на плоскости могут быть пересекающимися или параллельными. В случае параллельности прямые либо не имеют общих точек, либо совпадают.
Рассмотрим каждый из этих случаев.
Пример 1.
Решим систему уравнений:
{2х + у = -11,
{х – 2у = 8.
Решение.
Выразив из каждого уравнения у через х, получим систему:
{у = -3х – 11,
{у = 0,5х – 4.
Угловые коэффициенты прямых – графиков уравнений системы различны (-3 и 0,5), значит, прямые пересекаются.
Координаты точки их пересечения являются решением этой системы, единственным решением.
Пример 2.
Решим систему уравнений:
{3х – 2у = 12,
{6х – 4у = 11.
Решение.
Выразив из каждого уравнения у через х, получим систему:
{у = 1,5х – 6,
{у = 1,5х – 2,75.
Прямые у = 1,5х – 6 и у = 1,5х – 2,75 имеют равные угловые коэффициенты, значит эти прямые параллельны, причём прямая у = 1,5х – 6 пересекает ось у в точке (0; -6), а прямая у = 1,5х – 2,75 – в точке (0; -2,75), следовательно, прямые не имеют общих точек. Поэтому система уравнений не имеет решений.
В том, что данная система не имеет решений можно убедиться рассуждая следующим образом. Умножив все члены первого уравнения на 2, получим уравнение 6х – 4у = 24.
Сравнивая это уравнение со втором уравнением системы, видим, что левые части уравнений одинаковы, поэтому при тех же значениях х и у они не могут принимать различных значений (24 и 11). Следовательно, система

{6х – 4у = 11.
не имеет решений, значит, не имеет решений и система
{3х – 2у = 12,
{6х – 4у = 11.
Пример 3.
Решим систему уравнений:
{5х – 7у = 16,
{20х – 28у = 64.
Решение.
Разделив каждый член второго уравнения на 4, получим систему:
{5х – 7у = 16,
{5х – 7у = 16,
состоящую из двух одинаковых уравнений. Графики этих уравнений совпадают, поэтому координаты любой точки графика будут удовлетворять каждому из уравнений системы, то есть являться решением системы. Значит, данная система имеет бесконечное множество решений.
Если в каждом уравнении системы двух линейных уравнений с двумя переменными хотя бы один из коэффициентов при переменной не равен нулю, то система либо имеет единственное решение, либо имеет бесконечно много решений.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Количество решений системы линейных уравнений.
Теорема:
Всякая
система линейных уравнений или не имеет
решений, или имеет единственное решение,
или имеет бесконечное число решений.
Доказательство:
К
применим метод Гаусса, т.е. расширенная
матрица системы приводится к ступенчатому
виду. Если ступенька матрицы содержит
строку (0 0 … 0не
ноль), т.е.
имеющую только один последний ненулевой
элемент, то система будет иметь следствием
уравнение 0х1
+ … + 0хn
= не ноль,
которое не имеет решений, а значит и вся
система не имеет решений.
Если
ступенчатая матрица содержит длинную
ступеньку (длину > 1) и не выполнен
предыдущий рассмотренный случай

1
0
1
0
0 0 0 0
то,
очевидно, система будет иметь бесконечное
число решений, т.к. не начальным позициям
длинной ступени будут соответствовать
свободные переменные (одна или несколько),
которым можно придать любые значения.
И, наконец, если в ступенчатой матрице
все ступени, кроме последней, длины 1, а
последняя длины 2,
1
1
1
1
Система
будет очевидно иметь единственное
решение.
Теорема:
Если
в системе линейных уравнений число
уравнений меньше числа неизвестных, то
система не может иметь единственного
решения, и возможна только одна из 2-х
ситуаций: нет решений или бесконечное
число решений.
Доказательство:
В
ступенчатой форме расширенной матрицы
в случае единственного решения все
ступени до черты имеют длину 1, а значит
число строк расширенной матрицы (т.е.
число уравнений) не меньше числа столбцов
до черты (т.е. числа неизвестных).
Замечание:
Е
уравнений больше чем неизвестных, то
возможны все три указанные выше ситуации.
Приведем простые примеры:
x
+ y
= 2 х + y
= 2
x
+ y
= 3 — нет решений, x
– y
= 1 — одно решение,
x
+ y = 1 2x + 2y = 4
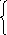
+ y
= 2
2x
+ 2y
= 4 — бесконечное число решений.
3x
+ 3y = 6
Выясним,
когда система n
уравнений с n
неизвестными будет иметь единственное
решение.
Теорема:
Система
n
линейных уравнений с n
неизвестными имеет единственное решение
тогда и только тогда, когда определитель
матрицы системы не
равен нулю.
Доказательство:
Р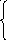
систему
а11
х1
+ … +
а1n
xn
= b1
…
an1
x1
+…
+ ann xn
= bn

решения системы можно применить метод
Крамера (или обратной матрицы) и, значит,
система имеет единственное решение.

… аn1
b1
Её
расширенная матрица: А = … …
an1
… annbn
Если
система имеет единственное решение, то
её расширенная матрица может элементарными
преобразованиями быть приведена к
такому ступенчатому виду:

0 0 … 0 b1

1 0 … 0 b2
А
0
0 … 1 bn
Ч
А до черты будет единичной матрицей.
Её определитель = 1.
З
что получен из элементарными
преобразованиями строк.
Нетрудно
проверить, что элементарные преобразования
не меняют свойства определителей быть
равными или не равными нулю.
О
= 1 = 0, а, следовательно, = 0.
Соседние файлы в папке ВЕЧЕРНЕЕ 1 семестр 2012
- #
- #
- #
Количество решений системы линейных уравнений
Количество
решений линейных уравнений
1.
Коэффициенты при переменных в уравнениях не
пропорциональны, т.е. . Система имеет единственное решение

2.
Коэффициенты при переменных в уравнениях
пропорциональны, т.е. , но они не пропорциональны свободным членам, т.е.
или
. Система не имеет решений.
3. Коэффициенты при переменных и свободные члены в
уравнениях пропорциональны, т.е. ,
,
. Система имеет бесконечно много решений: решением
является любая пара чисел (x,y), удовлетворяющая одному уравнению
системы.
Решение систем уравнений
Содержание:
Графический метод решения систем уравнений
Вспоминаем то, что знаем
Что такое график уравнения с двумя неизвестными?
Что представляет собой график линейного уравнения с двумя неизвестными?
Решите графическим методом систему линейных уравнений:

Решите графическим методом систему уравнений:
Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту
В курсе алгебры 7-го класса вы изучали системы линейных уравнений.
Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Начнём с графического метода
Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.
Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.
Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.
Возможно вам будут полезны данные страницы:
Примеры с решением
Пример 1:
Решим систему уравнений:
Построим графики уравнений
Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).

Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.
Ответ: (2; 5) и (-1; 2).
Пример 2:
Выясним количество решений системы уравнений:
Построим графики уравнений
Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.

Ответ: Два решения.
Решение систем уравнений методом подстановки
Вспоминаем то, что знаем
Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.
Решите систему линейных уравнений методом подстановки:
Открываем новые знания
Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?
Решите систему уравнений методом подстановки:
Как решить систему двух уравнений с двумя неизвестными методом подстановки?
Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?
Ранее вы решали системы уравнений первой степени.
Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.
Пример 3:
Пусть (х; у) — решение системы.
Выразим х из уравнения
Подставим найденное выражение в первое уравнение:
Решим полученное уравнение:
Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.
Чуть сложнее дело обстоит в следующем примере.
Пример 4:
Решим систему уравнений:
Пусть (х; у) — решение системы.
Выразим у из линейного уравнения:
Подставим найденное выражение в первое уравнение системы:
После преобразований получим:
Ответ: (-0,5; 0,5), (4; 5).
Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».
Пример 5:
Подставим во второе уравнение 
Теперь выразим х через у из первого уравнения системы:
Подставим в полученное ранее уравнение ху = 2:
Корни этого уравнения:

Иногда решить систему можно, используя метод алгебраического сложения.
Пример 6:
Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:

Корни этого уравнения:
Подставим найденные значения в первое уравнение. Рассмотрим два случая:
1)
2) 

Иногда упростить решение удаётся, используя различные варианты замены неизвестных.
Пример 7:
Решим систему уравнений:
Обозначим
Второе уравнение системы примет вид:
Решим полученное уравнение. Получим, умножая обе части на 2а:
Осталось решить методом подстановки линейные системы:
Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями
Напомним, что при решении задач обычно действуют следующим образом:
1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;
2) решают полученную систему;
3) отвечают на вопрос задачи.
Пример 8:
Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.
Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — 
Воспользуемся теоремой Пифагора:
Решим систему. Выразим из первого уравнения у:
Подставим во второе уравнение:
Корни уравнения:
Найдём
С учётом условия 
Пример 9:
Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.
Пусть х — первое число, у — второе число.
Тогда: 
Вычтем из второго уравнения первое. Получим:
Дальше будем решать методом подстановки:
Подставим в первое уравнение выражение для у:
Корни уравнения: 
Найдём у из уравнения:
Получим ответ: 16 и 7.
Симметричные системы уравнений с двумя неизвестными
Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение 



Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.
ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.
Например, если в системе уравнений
переставить местами неизвестные х и у, то получим систему:
Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.
Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:
Сначала научитесь выражать через неизвестные 
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
«Системы уравнений». 9-й класс
Класс: 9
Презентация к уроку
Загрузить презентацию (412 кБ)
При помощи учащихся класса были повторены способ подстановки и сложения. Графический – был рассмотрен вместе (слайды показывались на стене): дети рассказывали о функции и схематически изображали её график мелом, затем выцветал правильный и, было видно, прав ли ученик. В этом способе повторили нахождение координат данной точки, их запись.
Далее устно рассматривались решения различных тестовых заданий, где применялся графический способ решения систем уравнений.
В конце урока проводится маленькая самостоятельная работа с аналогичными заданиями.
Цели:
- повторить способы решения систем уравнений;
- акцентировать внимание на возможность решения систем различными способами;
- научить, при решении систем уравнений, записывать верно ответ
- продолжить обучать умению
- планировать самостоятельную работу;
- осваивать информацию и логически ее перерабатывать;
- вырабатывать собственную позицию, обосновывать ее и защищать (обосновывать свой способ решения, свой результат).
Оборудование:
- компьютер,
- мультимедийный проектор,
- карточки.
I этап урока (организационный)
Учитель сообщает тему урока, цели.
II этап урока (повторение)
1. Как вы понимаете выражение – «система уравнений»?
2. Что значит: решить систему уравнений? (Решить систему – это значит найти пару значений переменных, которая обращает каждое уравнение системы в верное равенство.)
3. Какие способы решения систем вы знаете? (Подстановки, сложения и графический.)
Вспомнить эти способы нам помогут …
Предварительно по работе с системами подготовлены и проверены ученики данного класса.
1. Способ подстановки
О решении систем этим способом рассказывает …
Далее вместе с классом решаем систему этим способом на доске и в тетради.

2. Способ сложения
О решении систем этим способом рассказывает …
Далее вместе с классом решаем систему этим способом на доске и в тетради.



3. Графический способ.
Рассказывает учитель с помощью всех учащихся.
Слайд 5
- Что нужно сделать для решения систем графическим способом? (Построить графики функций и найти координаты точек пересечения графиков. Для этого из каждого уравнения нужно выразить переменную у.)
- Выразим из обоих уравнений переменную у.
- Что можно сказать о первом уравнении? (Это уравнение функции обратной пропорциональности. График – гипербола, состоящая из двух ветвей, расположенных в первой и третьей координатных четвертях.)
- Как построить гиперболу? (Строим на доске, проверяем с помощью слайда)
- Что можно сказать о втором уравнении? (Это уравнение квадратичной функции. График – парабола, полученная из графика функции
путём перемещения на три единицы вверх по оси ординат.)
- Сколько точек пересечения получили? (1)
- Как найти её координаты?
- От чего зависит количество решений системы уравнений? (От количества точек пересечения графиков функций.)
Физминутка
Выполняем несколько заданий из материалов ГИА (по слайдам)
Задание №1. Слайд 6
Задание №2. Слайд 7
Задание №3. Слайд 8
Задание №4 Слайд 9
Задание №5. Слайд 10
Запишем домашнее задание: П 3.5, с 150.
№ 434 (а) – способ сложения;
№ 435 (а) – способ подстановки;
№ 436 (а) – графически.
III этап урока (заключительный)
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij
http://urok.1sept.ru/articles/627834
Цель урока: сформировать умение по
виду системы двух линейных уравнений с двумя
переменными определять количество решений
системы.
Задачи:
- Образовательные:
- повторить способы решения систем линейных
уравнений; - связать графическую модель системы с
количеством решений системы; - найти связь между соотношением коэффициентов
при переменных в системе и количеством решений.
- повторить способы решения систем линейных
- Развивающие:
- формировать способности к самостоятельным
исследованиям; - развивать познавательный интерес учащихся;
- развивать умение выделять главное,
существенное.
- формировать способности к самостоятельным
- Воспитательные:
- воспитывать культуру общения; уважение к
товарищу, умение достойно вести себя. закреплять
навыки работы в группе; - формировать мотивацию на здоровый образ жизни.
- воспитывать культуру общения; уважение к
Тип урока: комбинированный
ХОД УРОКА
I. Организационный момент (нацелить
учащихся на урок)
– На предыдущих уроках мы научились решать
системы двух линейных уравнений с двумя
переменными разными способами. Сегодня на уроке
нам предстоит ответить на вопрос: «Как, не решая
систему уравнений определить, сколько же решений
она имеет?», поэтому тема урока называется
«Исследование системы линейных уравнений с
двумя переменными на количество решений ». Итак,
начнём урок. Соберёмся с силами. В четыре приёма
глубоко вдохнём воздух через нос и в пять приёмов
с силой выдохнем, задувая воображаемую свечку.
Повторим это 3 раза. Очень быстро активизируем
свой мозг. Для этого интенсивно промассажируем
межбровную точку: указательным пальцем правой
руки делаем 5 круговых движений в одну сторону и в
другую. Повторим это 2-3 раза.
II. Проверка домашнего задания
(коррекция ошибок)
Показать решение системы разными способами:
А) методом подстановки;
Б) Методом сложения;
В) по формулам Крамера;
Г) Графически.
Пока на доске готовятся к ответам по домашнему
заданию, с остальными учениками начинается
подготовка к следующему этапу урока.
III. Этап подготовки к усвоению нового
материала (актуализация опорных знаний)
– Если вы знаете ответы на вопросы, но вдруг
растерялись и всё сразу забыли, попробуйте
собраться, убедить себя, что вы всё знаете и у вас
всё получится. Хорошо помогает обыкновенный
массаж всех пальцев. Во время обдумывания
массажируйте все пальчики от основания к ногтю.
– Что называют системой двух уравнений?
– Что значит решить систему линейных
уравнений?
– Что является решением системы линейных
уравнений?
– Будет ли пара чисел (– 3; 3) решением системы
уравнений:
– Расскажите, в чём суть каждого известного вам
способа решения систем линейных уравнений с
двумя переменными. (Рекомендуется общение в
парах)
Ответы учеников сопровождаются показом
слайдов 1-14 (Презентация)
учителем. (можно одним из учеников). Проверяем
домашнее задание (слушаем ответы учеников у
доски).
Учитель: Для решения специфических
систем уравнений существует ещё один способ,
называется он методом подбора решения.
Попробуйте, не решая подобрать решение системы
уравнений: .
Объясните суть метода.
– Найдите решение системы уравнений:
а)
б) в)
– Дано уравнение a + b =15, добавьте такое
уравнение, чтобы решением полученной системы
была пара чисел (– 12; 27)
Перечислите ещё раз все способы решения систем
линейных уравнений, с которыми вы познакомились.
IV. Этап усвоения новых знаний
(исследовательская работа)
– Прежде чем переходить к следующему этапу
урока, немного отдохнём.
Сидя на стуле – расслабьтесь, примите позу
пиджака, висящего на вешалке,
«Постреляйте» глазами в соседей. А затем
вспомним про «царственную осанку»: спина прямая,
мышцы головы без напряжения, выражение лица
очень значительное, соберёмся с мыслями, для чего
сделаем массаж межбровной точки или пальчиков и
приступим к дальнейшей работе.
Учитель: Мы научились решать системы
линейных уравнений с двумя переменными разными
способами и знаем, что система таких уравнений
может иметь:
А) одно решение;
Б) не иметь решений;
В) много решений.
А нельзя ли, не прибегая к решению, ответить на
вопрос: сколько же решений имеет система
уравнений? Сейчас мы с вами проведём
небольшое исследование.
Для начала разобьемся на три исследовательские
группы. Составим план нашего исследования,
ответив на вопросы:
1) Что представляет собой графическая модель
системы линейных уравнений с двумя переменными?
2) Как могут располагаться две прямые на
плоскости?
3) Как зависит количество решений системы от
расположения прямых?
(После ответов учащихся используем слайды 6-10 Презентации.)
Учитель: Значит основа нашего
исследования состоит в том, чтобы по виду системы
понять, как располагаются прямые.
Каждая исследовательская группа решает эту
задачу на конкретной системе уравнений по плану (Приложение 1).
Система для группы №1.
Система для группы №2.
Система для группы №3.
На выполнение работы даётся 5 минут, затем
делимся своими выводами с одноклассниками. (Приложение 2), а также
обращаемся к слайдам 15-17 Презентации.
V. Релаксация
Предлагаю отдохнуть, расслабиться:
физкультминутка или психологический тренинг. (Приложение 3)
VI. Закрепление нового материала
А) Первичное закрепление
Используя полученные выводы, ответьте на
вопрос: сколько решений имеет система уравнений
а)
б)
в)
Итак, прежде чем решать систему, можно узнать,
сколько она имеет решений.
Б) решение более сложных задач по новой теме
1) Дана система уравнений
– При каких значениях параметра a данная
система имеет единственное решение?
(Работа выполняется в группах по 4 человека:
пары поворачиваются друг к другу)
– При каких значениях параметра a данная
система не имеет решений?
– При каких значениях параметра данная система
уравнений имеет много решений?
2) Дано уравнение – 2x + 3y = 12
Добавьте ещё одно уравнение так, чтобы система
этих уравнений имела:
А) одно решение;
Б) бесконечно много решений.
3) Провести полное исследование системы
уравнений на наличие её решений:
VII. Рефлексия. Методика «Мухомор»
На дополнительной доске (или на отдельном
плакате) нарисован круг, разбитый на секторы.
Каждый сектор – это вопрос, рассмотренный на
уроке. Ученикам предлагается
поставить точку:
- ближе к центру, если ответ на вопрос не вызывает
сомнения; - в середину сектора, если сомнения есть;
- ближе к окружности, если вопрос остался не
понятым; (Приложение 4)
VIII. Домашнее задание
Алгебра-7, под редакцией Теляковского.
Параграфы 40-44, №1089,1095а), решать любым способом.
Выяснить, при каком значении a система имеет одно
решение, много решений, не имеет
решений
– Итак: наш урок подошёл к концу. Приготовим
себя к перемене: сцепите руки замком, положите их
на затылок. Положите голову на парту, резко
сядьте прямо, примите «царственную» позу.
Повторите это ещё раз.
– Урок окончен. Всем спасибо. Подойдите к доске
и сделайте отметку на предложенном рисунке. До
свидания.




































































































 путём перемещения на три единицы вверх по оси ординат.)
путём перемещения на три единицы вверх по оси ординат.)