Сколько осей симметрии у круга?
оси симметрии круга Они бесконечны. Эти оси делят любую геометрическую форму на две точно равные половины.
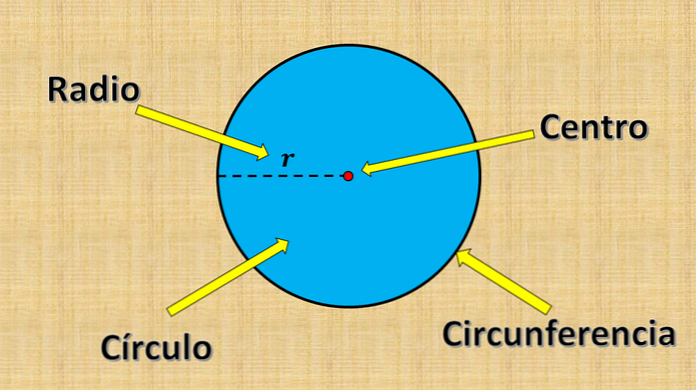
И круг состоит из всех точек, чье расстояние до фиксированной точки меньше или равно некоторому значению «r».
Упомянутая выше фиксированная точка называется центром, а значение «r» называется радиусом. Радиус — это наибольшее расстояние, которое может быть между точкой на окружности и центром..
С другой стороны, любой отрезок, концы которого находятся на краю окружности (окружности) и проходит через центр, называется диаметром. Его измерение всегда равно удвоенному радиусу.
Круг и окружность
Не путайте круг с кругом. Окружность относится только к точкам, которые находятся на расстоянии «r» от центра; то есть только край круга.
Однако при поиске осей симметрии безразлично, работаете ли вы с кругом или с кругом.
Что такое ось симметрии?
Ось симметрии — это линия, которая делит на две равные части определенную геометрическую фигуру. Другими словами, ось симметрии действует как зеркало.
Валы симметрии круга
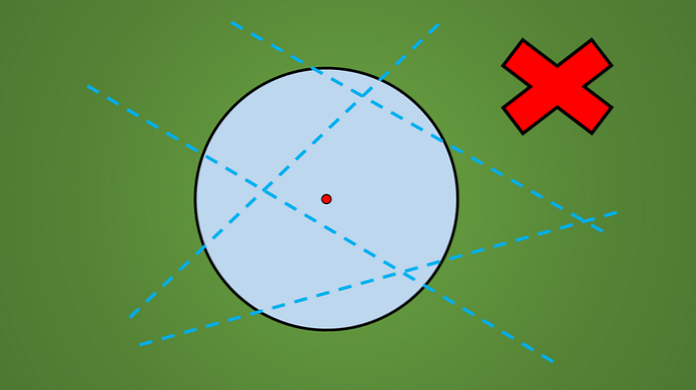
Если вы наблюдаете любой круг, независимо от его радиуса, вы можете видеть, что не каждая линия, которая пересекает его, является осью симметрии..
Например, ни одна из линий, нарисованных на следующем рисунке, не является осью симметрии..
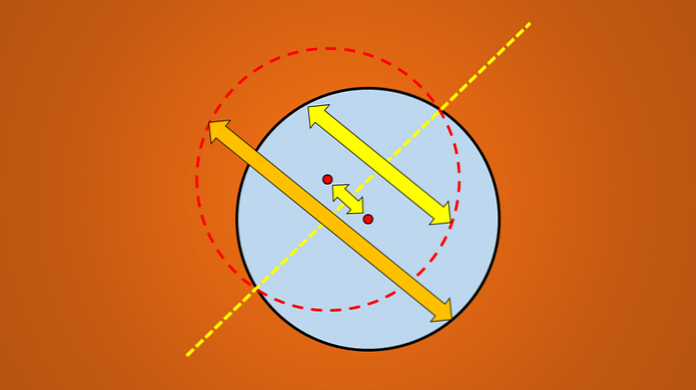
Простой способ проверить, является ли линия осью симметрии или нет, состоит в том, чтобы перпендикулярно отразить геометрическую фигуру к противоположной стороне линии..
Если отражение не соответствует исходному рисунку, то эта линия не является осью симметрии. Следующее изображение иллюстрирует эту технику.
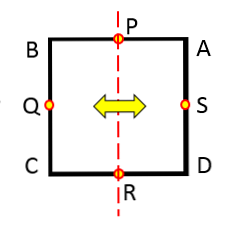
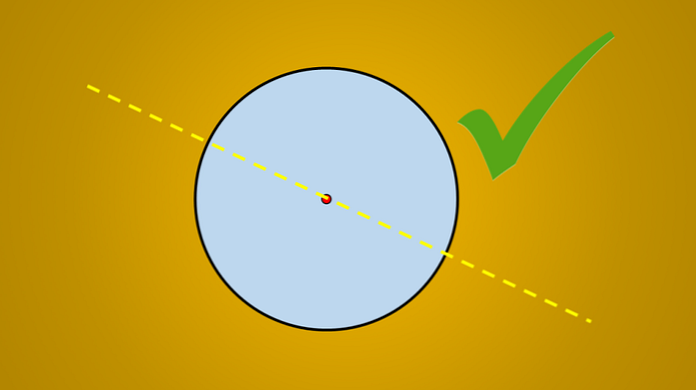
Но если рассматривается следующее изображение, хорошо известно, что нарисованная линия является осью симметрии круга.
Вопрос: есть ли еще оси симметрии? Ответ — да. Если повернуть эту линию на 45 ° против часовой стрелки, полученная линия также является осью симметрии круга.
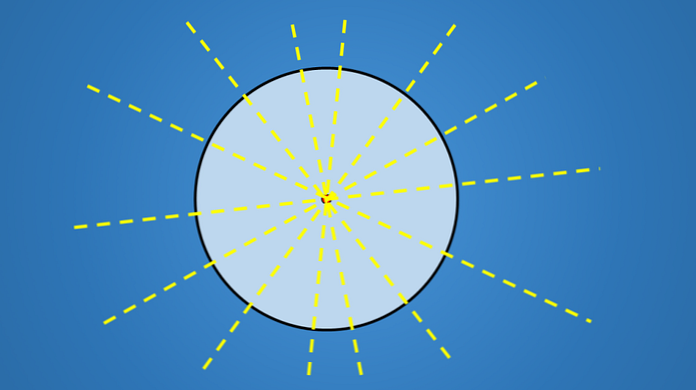
То же самое происходит, если вы поворачиваете на 90 °, 30 °, 8 ° и вообще на любое количество градусов.
Важной особенностью этих линий является не склонность, которую они имеют, но все они проходят через центр круга. Следовательно, любая линия, содержащая диаметр окружности, является осью симметрии..
Таким образом, поскольку круг имеет бесконечное число диаметров, то он имеет бесконечное количество осей симметрии.
Другие геометрические фигуры, такие как треугольник, четырехугольник, пятиугольник, шестиугольник или любой другой многоугольник, имеют конечное число осей симметрии.
Причина, по которой круг имеет бесконечное число осей симметрии, заключается в том, что у него нет сторон.
Осевая и центральная симметрия
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Симметрия окружности
Есть ли симметрия в окружности? Сколько осей симметрии имеет окружность? Что является центром симметрии окружности?
Окружность имеет бесконечно много осей симметрии.
Осью симметрии окружности является любая прямая, содержащая диаметр окружности.
Проведём произвольный диаметр AB окружности.
Отметим на окружности произвольную точку X.
Из точки X проведём хорду, перпендикулярную диаметру.
Обозначим точки пересечения этой прямой с диаметром AB как P и X1.
Так как хорда перпендикулярна диаметру, то диаметр проходит через середину.
Следовательно, XP=X1P, а значит, точка X1 симметрична точке X относительно прямой, содержащей диаметр AB.
Имеем: точка, симметричная произвольной точке окружности относительно произвольного диаметра, также принадлежит окружности. Следовательно, любой диаметр окружности является её осью симметрии.
Что и требовалось доказать .
Окружность — центрально-симметричная фигура.
Осью симметрии окружности является её центр.
Отметим на окружности произвольную точку X.
Проведем через точку X диаметр XX1.
XO=X1O (как радиусы).
Таким образом, точка, симметричная произвольной точке окружности относительно её центра, также принадлежит окружности. Значит, окружность — центрально-симметричная фигура, а центр симметрии окружности — это центр окружности.
http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
Опыты с зеркалами, которые мы проводили на прошлом занятии,
позволили нам прикоснуться к удивительному миру симметрии.
В переводе с греческого слово «симметрия» означает
«соразмерность, пропорциональность, одинаковость в расположении частей».
Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то,
что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким
образом…
А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то
отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как
исходная фигура).
Поэтому такая симметрия называется зеркальной (или осевой,
если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало,
называется осью симметрии.
Если симметричную фигуру сложить пополам вдоль оси симметрии, то
её части совпадут.
С симметрией мы постоянно встречаемся в повседневной жизни. Люди
используют симметрию в орнаментах, предметах быта, технике. Издавна человек
использовал симметрию в архитектуре. Древним храмам, башням средневековых
замков, современным зданиям она придаёт гармоничность, законченность. Симметрия
также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.
Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил.
Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии
кляксы.
Получается, что клякса имеет одну (вертикальную) ось симметрии.
А вот у снежинки 6 линий сгиба и все они являются осями симметрии.
У геометрических фигур может быть одна или несколько осей
симметрии, а может и не быть совсем.
Так, прямоугольник обладает двумя осями симметрии, каждая
из которых проходит через середины двух его противоположных сторон. То есть,
вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии,
половинки фигуры совпадут.
Ромб также обладает двумя осями
симметрии. Это прямые, которые содержат его диагонали.
Квадрат имеет четыре оси симметрии.
Две проходят через середины его противоположных сторон. И ещё две – это прямые,
которые содержат его диагонали.
Круг. Его осью симметрии является
любая прямая, которая проходит через его центр, то есть содержит диаметр круга.
А значит, круг имеет бесконечно много осей симметрии
Теперь посмотрите на следующую фигуру. Это произвольный
параллелограмм. У него нет ни одной оси симметрии.
У произвольного треугольника тоже нет осей симметрии.
У равнобедренного треугольника есть одна ось симметрии.
У равностороннего (то есть у правильного) треугольника
– три оси симметрии.
Теперь посмотрите на шестиугольник. У него три оси симметрии,
которые проходят через противоположные вершины, и ещё три оси, которые проходят
через середины противоположных сторон. То есть всего шесть осей симметрии.
Таким образом, мы можем сказать, что круг – «самая
симметричная» фигура из рассмотренных, так как он имеет бесконечно много
осей симметрии.
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из
них лишняя.
Итак, первая фигура напоминает замочную скважину. Она имеет одну
ось симметрии.
Вторая фигура тоже имеет одну ось симметрии.
У третьей фигуры (в виде буквы Т) одна ось симметрии.
У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси
симметрии. И поэтому она лишняя.
Теперь давайте посмотрим на следующие пять фигур. Что у них
общего?
Первая фигура – круг. Выше мы выяснили, что у круга бесконечно
много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось
симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая
фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая
фигура имеет хотя бы одну ось симметрии.
На предыдущем занятии мы с вами проводили опыт с двумя плоскими
зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали
симметричные фигуры.
Давайте изобразим в виде прямых два зеркала под углом друг к
другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь
настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы
при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно,
что угол ними равен .
Посмотрите на рассмотренные выше фигуры, которые имеют две оси
симметрии. Угол между осями равен .
Если, например, мы поставим зеркала под углом друг к
другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси
симметрии.
Давайте научимся точно строить отражение фигуры в зеркале.
Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную и построим
её отражение в зеркале.
Итак, из вершин ,
и
опускаем перпендикуляры на прямую l. Затем продолжаем их «за
зеркало» на такое же расстояние (равное длине соответствующего отрезка).
Получаем точки ,
и
. Соединяем
эти точки. Ломаная является
отражение ломаной .
Можно сказать, что ломаная симметрична
ломаной относительно
прямой l.
Построим с вами треугольник, симметричный треугольнику относительно
прямой l.
Из вершин и
опустим
перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние
(равное длине соответствующего отрезка). Получим точки и
.
При этом точка осталась на
месте. Она лежит на оси симметрии. Она симметрична сама себе. и
симметричны
относительно прямой l.
А сейчас посмотрите на рисунок.
Давайте выясним, симметрична ли точка точке
относительно
прямой l. Для этого мы соединим точки и
. Затем с
помощью угольника проверим, перпендикулярна ли прямая l отрезку . Перпендикулярна.
Потом с помощью линейки проверим, делит ли прямая l отрезок и
пополам. Делит.
Значит, точки и
симметричны
относительно прямой l.
Кроме симметрии относительно прямой существует ещё симметрия
относительно точки, так называемая центральная симметрия. Она
характеризуется наличием центра симметрии – точки О, которая обладает
определённым свойством. Можно сказать, что точка О является центром
симметрии, если при повороте вокруг точки О на фигура
переходит сама в себя.
Понятие центральной симметрии распространяется и на трёхмерное
пространство.
Проверить, является ли фигура центрально-симметричной или нет,
можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем,
проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру
на вокруг
иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.
Сейчас посмотрите на плоские фигуры, которые имеют и центр
симметрии, и оси симметрии.
Это круг. Выше мы сказали, что он имеет бесконечно много
осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии
круга является его центр.
Квадрат имеет четыре оси симметрии.
Центром симметрии квадрата является точка пересечения его диагоналей.
У шестиугольника шесть осей симметрии. Центром его
симметрии является точка пересечения его диагоналей.
Выше мы сказали, что произвольный параллелограмм не имеет
ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его
диагоналей.
А вот, например, равнобедренный треугольник имеет ось
симметрии, но не имеет центра симметрии. То же самое можно сказать и про
пятиугольник, у которого есть оси симметрии, но центра симметрии нет.
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Видео
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Теги
Что такое ось симметрии
Каким бы субъективным ни было понятие красоты, оно все-таки имеет некоторые общие для всех критерии. Один из таких критериев – симметрия, ведь мало кому понравится лицо, на котором глаза расположены на разном уровне. Симметрия же всегда предполагает наличие поворотной оси, именуемой также осью симметрии.

В широком смысле симметрией именуется сохранение чего-либо неизменным при каких-то преобразованиях. Обладают таким свойством и некоторые геометрические фигуры.
Применительно к геометрической фигуре симметрия означает, что если данную фигуру преобразовать – например, повернуть – некоторые ее свойства останутся прежними.
Возможность таких преобразований различается от фигуры к фигуре. Например, круг можно сколько угодно вращать вокруг точки, расположенной в его центре, он так и останется кругом, ничто для него не изменится.
Понятие симметрии можно объяснить, не прибегая к вращению. Достаточно провести через центр круга прямую и построить в любом месте фигуры перпендикулярный ей отрезок, соединяющий две точки на окружности. Точка пересечения с прямой будет делить данный отрезок на две части, которые будут равны друг другу.
Иными словами, прямая разделила фигуру на две равные части. Точки частей фигуры, расположенные на прямых, перпендикулярных данной, находятся на равном расстоянии от нее. Вот эта пряма и будет называться осью симметрии. Симметрия такого рода – относительно прямой – называется осевой симметрией.
У разных фигур количество осей симметрии будет различным. Например, у круга и шара таких осей множество. У равностороннего треугольника осью симметрии будет перпендикуляр, опущенный на каждую из сторон, следовательно, у него три оси. У квадрата и прямоугольника можно провести четыре оси симметрии. Две из них перпендикулярны сторонам четырехугольников, а две другие являются диагоналями. А вот у равнобедренного треугольника ось симметрии только одна, располагающаяся меду равными его сторонами.
Осевая симметрия встречается и в природе. Ее можно наблюдать в двух вариантах.
Первый вид – радиальная симметрия, предполагающая наличие нескольких осей. Она характерна, например, для морских звезд. Более высокоразвитым организмам присуща билатеральная, или двусторонняя симметрия с единственной осью, делящей тело на две части.
Человеческому телу тоже присуща билатеральная симметрия, но идеальной ее назвать нельзя. Симметрично расположены ноги, руки, глаза, легкие, но не сердце, печень или селезенка. Отклонения от билатеральной симметрии заметны даже внешне. Например, крайне редко бывает так, чтобы у человека на обеих щеках были одинаковые родинки.
Источники:
- Что такое симметрия
Если середину отрезка провести перпендикулярную прямую, то она будет осью симметрии данного отрезка.
Есть утверждения, что если через этот отрезок провести прямую, то она будет второй осью симметрии для данного отрезка.
Давайте рассмотрим более подробнее этот случай и для начала ознакомимся с определением некоторых вещей
Определение точки
Определение линии
Определение прямой
Определение отрезка
Отрезок — это часть прямой линии, он имеет длину, но не имеет ширины и толщины, следовательно — разделить его вдоль никак нельзя и поэтому, он имеет только одну ось симметрии.
Теперь рассмотрим случай с прямой.
Проведем две перпендикулярных прямых к прямой а — одну посередине отрезка АА1, который лежит на этой прямой, другую немного правее
Первая прямая будет осью симметрии и для отрезка АА1 и для прямой а, вторая — только для прямой а (для любых точек А и А1 всегда найдем симметричные).
Прямая линия имеет бесконечное количество осей симметрии, но все они должны быть к ней перпендикулярны.