Как найти количество гомоморфизмов - AvtoShod.ru

Будем считать известным тот факт, что из $%mathbb Z_m$% в $%mathbb Z_n$% имеется в точности $%d$% гомоморфизмов, где $%d=НОД(m,n)$%. Доказательство там простое, и эта тема много раз звучала на данном форуме.

1) Если дан гомоморфизм прямой суммы в абелеву группу, то он задаёт гомоморфизмы прямых слагаемых (это верно даже при отсутствии абелевости), и обратно: набор гомоморфизмов слагаемых задаёт итоговый гомоморфизм прямой суммы (тут абелевость уже требуется). Поэтому в пункте а) надо перемножить три наибольших общих делителя, они все равны 2, и получается ответ 8.

В пункте б) нужно подсчитать число решений уравнения $%10x=0$% в $%A$%. Эта задача сводится к подсчёту числа решений для каждого из слагаемых, и там получаются не же НОД’ы. Поэтому в прямой сумме число решений уравнения также равно произведению, и гомоморфизмов снова будет 8.

По поводу пункта в): инъективный гомоморфизм возможен только тогда, когда порядок одной из групп делит порядок другой, но этого нет ни в котором из случаев. Сюръективности там тоже нет, поскольку в этом случае мы группу большего порядка отображаем на группу меньшего порядка, но 10 не делит порядок большей группы.

2) В пункте а), как и выше, рассматриваем гомоморфизмы отдельных слагаемых. Для циклической группы порядка $%m$% получится столько гомоморфизмов, сколько решений имеет в $%D_{100}$% уравнение $%x^m=1$%. Группа диэдра состоит из поворотов и осевых симметрий. Повороты образуют циклическую группу порядка 100, и уравнение имеет $%НОД(m,100)$% решений в группе поворотов, то есть 2, 2, 4 для каждого слагаемого. В то же время, все осевые симметрии в количестве 100 штук везде подходят, и общий ответ равен $%102cdot102cdot104$%.

Для решения пункта б) заметим, что ядро всякого гомоморфизма в абелеву группу содержит коммутант, поэтому гомоморфизмов для всей группы будет столько же, как и для факторгруппы по коммутанту. Известно, что для группы $%D_n$% коммутант равен подгруппе поворотов индекса 2, то есть надо найти число гомоморфизмов $%mathbb Z_2$% в прямую сумму, и легко видеть, что их будет 8.

Источник

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

	Найти число гомоморфизмов 08.11.2009, 23:31
08/10/08 30	Пусть ,где Во всех задачах, приведенных ниже , нужно найти число гомоморфизмов. 1. $f: <a>_{21} to <b>_{42}$ , при этом ${f(a^{18})}=b^{12}$ Решение: ${f(a^{18})}=(b^x)^{18}=b^{12}$ Решим уравнение: , , , Ответ: 3 гомоморфизма.Правильный ли ответ? 2. $f: <a>_{21} to <b>_{42}times <c>_{15}$ Как подойти не знаю.. 3. $f: (mathbb{Z}_{10},+)times (mathbb{Z}_{25},+) to {mathbb{Z}_{31}^*}$ аналогично.. 4. Найти все эдоморфизмы циклической группы $<a>_{40}$ , такие,что $f(a^{15})ne 1$ ____________________________________________________________________ Помогите пожалуйста разобраться в задачах.

VAL

Re: Найти число гомоморфизмов

09.11.2009, 01:04

Заслуженный участник

27/06/08
4051
Волгоград

А почему при Вы модуль на 3 поделили?
А откуда 70 взялось? Когда обе части сравнения умножают на число взаимно простое с модулем, сам модуль не трогают. Просто единственный класс вычетов, удовлетворяющий сравнению по приведенному модулю, надо разбросать на несколько классов по исходному.

Это замечания по поводу решения сравнения. Но, само по себе решение сравнения не гарантирует нахождения гомоморфизма.

Цитата:

Ответ: 3 гомоморфизма. Правильный ли ответ?

Даже если правильный, то много ли он стоит при неправильном решении?

Цитата:

4. Найти все эдоморфизмы $f$ циклической группы $<a>_{40}$ , такие,что $f(a^{15})ne 1$ .

А сколько всего существует эндоморфизмов циклической группы из 40 элементов? Что достаточно указать, чтобы задать эндоморфизм?

Gilb007	Re: Найти число гомоморфизмов 09.11.2009, 01:46
08/10/08 30	Цитата: А почему при Вы модуль на 3 поделили? Вы правы,исправляю.. $f: <a>_{21} to <b>_{42}$ , при этом ${f(a^{18})}=b^{12}$ Решение: ${f(a^{18})}=(b^x)^{18}=b^{12}$ Решим уравнение: , , , По идеи теперь получается 6. Цитата: Но, само по себе решение сравнения не гарантирует нахождения гомоморфизма. А что гарантирует? Цитата: А сколько всего существует эндоморфизмов циклической группы из 40 элементов? Что достаточно указать, чтобы задать эндоморфизм? Известно,что эндоморфизм-это гомоморфизм на себя. По теореме о гомоморфизме ${frac{<a>_{40}}{ker f}}cong Im f$ , получаем дальше идут непонятки..

VAL

Re: Найти число гомоморфизмов

09.11.2009, 20:22

Заслуженный участник

27/06/08
4051
Волгоград

Цитата:

А почему при Вы модуль на 3 поделили?

Вы правы,исправляю..

$f: <a>_{21} to <b>_{42}$ , при этом ${f(a^{18})}=b^{12}$
Решение:
${f(a^{18})}=(b^x)^{18}=b^{12}$

Решим уравнение:
,
,
,

По идеи теперь получается 6.

Сравнение решено верно. Но не исходная задачка.

Цитата:

Но, само по себе решение сравнения не гарантирует нахождения гомоморфизма.

А что гарантирует?

Дело в том, что порождающий элемент группы $<a>_{21}$ может при гомоморфизме переходить не в любой элемент группы $<b>_{42}$ .
Например, предположим, что . Пусть $e$ и $e'$ — нейтральные элементы групп $<a>_{21}$ и $<b>_{42}$ . Тогда по свойству гомоморфизма $f(e)=f(a^{21})=(b^3)^{21}=b^{42}cdot b^{21} = b^{21} ne e'$ , что при гомоморфизме невозможно. Таким образом, гомоморфизма, при котором не существует.

Цитата:

Известно,что эндоморфизм-это гомоморфизм на себя.
По теореме о гомоморфизме ${frac{<a>_{40}}{ker f}}cong Im f$

, получаем

Это верно.

Цитата:

дальше идут непонятки..

А в какие элементы группы $<a>_{40}$ может переходить $a$ , так чтобы это отображение можно было продолжить до эндоморфизма $<a>_{40}$ , скажем, на подгруппу из 10 элемнтов?

Gilb007	Re: Найти число гомоморфизмов 10.11.2009, 02:54
08/10/08 30	Цитата: Дело в том, что порождающий элемент группы $<a>_{21}$ может при гомоморфизме переходить не в любой элемент группы $<b>_{42}$ . Например, предположим, что . Пусть и — нейтральные элементы групп $<a>_{21}$ и $<b>_{42}$ . Тогда по свойству гомоморфизма $f(e)=f(a^{21})=(b^3)^{21}=b^{42}cdot b^{21} = b^{21} ne e'$ , что при гомоморфизме невозможно. Таким образом, гомоморфизма, при котором не существует. Val ,это натолкнуло на следущие рассуждения!А что если решить еще одно сравнение? ${f(a^{21})}=(b^x)^{21}$ , , $begin{cases}x=0,2,4,6,..,10,..,24,..,38,40 (mod 42),\x=3,10,17,24,31,38 (mod 42) .end{cases}$ Это,похоже,обосновывает выбор 10,24 и 38 )) Значит при таком решение 3 гомоморфизма. Цитата: А в какие элементы группы $<a>_{40}$ может переходить , так чтобы это отображение можно было продолжить до эндоморфизма $<a>_{40}$ , скажем, на подгруппу из 10 элемнтов? На этот вопрос отвечу чуть позже.

Gilb007	Re: Найти число гомоморфизмов 10.11.2009, 20:15
08/10/08 30

VAL

Re: Найти число гомоморфизмов

10.11.2009, 22:39

Заслуженный участник

27/06/08
4051
Волгоград

Это,похоже,обосновывает выбор 10,24 и 38 ))

Похоже.

— 11 ноя 2009, 00:49 —

Это верно.

Цитата:

Для гомоморфизма справедливо .

А не наоборот?

Цитата:

Конечно! Нейтральный элемент может переходить только в нейтральный.

Цитата:

$f(a^{20})=a^{20}$

А это с чего? Куда обязаны переходить все элементы ядпр?

Цитата:

Т.о элементам $a^{10},a^{30}$ при таком гомоморфизме (где порядок образа равен 10) просто некуда переходить..

Как это!? Что это за гомоморфизм, при котором отображаются не все элементы исходной группы?!

Цитата:

Значит при такой подгруппе только один гомоморфизм?

Нет.
Рассмотрите, в какой элемент должен перейти $a$ , чтобы вся группа перешла в $H$ , точнее НА $H$ .

Gilb007	Re: Найти число гомоморфизмов 11.11.2009, 04:21
08/10/08 30	Цитата: А не наоборот? Я тоже тогда засомневался.Значит правильно,если . Цитата: А это с чего? Куда обязаны переходить все элементы ядра? Ну вообще-то все элементы ядра должны переходить в нейтральный элемент,т.е $f(a^{10})=a^0$ $f(a^{20})=a^0$ $f(a^{30})=a^0$ Цитата: Нет. Рассмотрите, в какой элемент должен перейти , чтобы вся группа перешла в , точнее НА . Я так понимаю,что это принципиально важный момент в переходе порождающего элемента из $<a>_{40}$ . Значит порождающий элемент из $<a>_{40}$ (число их равно ) должен перейти в порождающий элемент (число их равно ,в табличке видны какие это элементы). Например,если рассмотреть такой гомоморфизм: $aker f={a^1,a^{11},a^{21},a^{31}} to a^4$ $a^3ker f={a^3,a^{13},a^{23},a^{33}} to a^{12}$ $a^7ker f={a^7,a^{17},a^{27},a^{37}} to a^{28}$ $a^9ker f={a^9,a^{19},a^{29},a^{39}} to a^{36}$ Получается,что по сути нужно рассмотреть различных гомоморфизмов перехода от порождающих элементов фактор-группы в порождающие группы ? Val ,огромное Вам спасибо,что помогаете разобраться в задачах!!

VAL

Re: Найти число гомоморфизмов

11.11.2009, 21:03

Заслуженный участник

27/06/08
4051
Волгоград

Цитата:

А это с чего? Куда обязаны переходить все элементы ядра?

Ну вообще-то все элементы ядра должны переходить в нейтральный элемент,т.е

$f(a^{10})=a^0$
$f(a^{20})=a^0$
$f(a^{30})=a^0$

Конечно!

Цитата:

Рассмотрите, в какой элемент должен перейти $a$ , чтобы вся группа перешла в $H$ , точнее НА $H$ .

Я так понимаю,что это принципиально важный момент в переходе порождающего элемента из $<a>_{40}$ .

Я бы даже сказал — определяющий.

Цитата:

Откуда взялось 24?
Вы отобразили $a$ в $a^4$ . Нужно ли после этого указывать куда перешли остальные порождающие элементы? Тем боле, что по определению циклической группы, порождающий элемент только один!
Нет, Вы, конечно, правы, что в качестве порождающего можно взять любой из 16-и подходящих элементов. Но если мы уже взяли какой-то, зачем нам остальные 15?

Gilb007	Re: Найти число гомоморфизмов 12.11.2009, 18:09
08/10/08 30	Цитата: Откуда взялось 24? Ну я вот как подумал…Рассмотрел фактор-группу $frac {<a>_{40}}{ker f}$ и группу .В обоих группах по 4-ре порождающих элементa.А число получилась как множество всех перестановок из -х элементов (мощность ). Цитата: Вы отобразили в . Нужно ли после этого указывать куда перешли остальные порождающие элементы? Тем боле, что по определению циклической группы, порождающий элемент только один! Нет, Вы, конечно, правы, что в качестве порождающего можно взять любой из 16-и подходящих элементов. Но если мы уже взяли какой-то, зачем нам остальные 15? Очень похоже на правду.Тогда смею предположить,что число гомоморфизмов по такой подгруппе будет равно 4-м. Т.е берем любой из 16-ти порождающих элементов $<a>_{40}$ ,но перейти-то но может в один из четырех порождающих .

VAL

Re: Найти число гомоморфизмов

12.11.2009, 21:00

Заслуженный участник

27/06/08
4051
Волгоград

Очень похоже на правду.

Такое иногда случается: правда похожа на правду

Цитата:

Тогда смею предположить,что число гомоморфизмов по такой подгруппе будет равно 4-м.
Т.е берем любой из 16-ти порождающих элементов $<a>_{40}$ ,но перейти-то но может в один из четырех порождающих $H$ .

Угу. Причем я (чтобы не усложнять себе жизнь) ограничился бы рассмотрением в качестве любого из порождающих элемента. .
Итак, одну ключевую мысль мы, надеюсь, зафиксировали. Для задания эндоморфизма, достаточно указать образ элемента .

Следующий вопрос (после правильного ответа на который до решения рукой подать): в любой ли элемент $<a>_{40}$ можно отобразить ?

Gilb007	Re: Найти число гомоморфизмов 13.11.2009, 20:37
08/10/08 30	Цитата: Следующий вопрос (после правильного ответа на который до решения рукой подать): в любой ли элемент $<a>_{40}$ можно отобразить ? Эм…Не совсем может понял вашего вопроса,но предполагаю,что вы имеете ввиду отображение порождающего элемента из $<a>_{40}$ в любой порождающий элемент из .Или что-то другое?

VAL

Re: Найти число гомоморфизмов

14.11.2009, 00:46

Заслуженный участник

27/06/08
4051
Волгоград

Цитата:

Эм…Не совсем может понял вашего вопроса,но предполагаю,что вы имеете ввиду отображение порождающего элемента из $<a>_{40}$ в любой порождающий элемент из $H$ . Или что-то другое?

Нет. $H$ уже проехалаи. Эта подгруппа ведь была выбрана просто для примера (см. соответствующий пост). Прямого отношения к решению задачи она не имеет. Цель была разобраться: чем определяется каждый эндоморфизм $<a>_{40}$ и сколько всего эндоморфизмов у этой группы.

Gilb007	Re: Найти число гомоморфизмов 14.11.2009, 07:51
08/10/08 30	Цитата: Нет. уже проехали. Эта подгруппа ведь была выбрана просто для примера (см. соответствующий пост). Прямого отношения к решению задачи она не имеет. Цель была разобраться: чем определяется каждый эндоморфизм $<a>_{40}$ и сколько всего эндоморфизмов у этой группы. А,понял) С эндоморфизмами благодаря вам уже разобрался,но в той задачке есть ограничение,что $f(a^{15})ne 1$ .На всякий случай напишу,что всего эндоморфизмов (без ограничения) 40 штук получается. В течение дня подумаю как дорешать задачку..

Gilb007	Re: Найти число гомоморфизмов 16.11.2009, 22:27
08/10/08 30	Сорри,оперативно не смог ответить. значит эндоморфизмы.. Т.к есть ограничение $f(a^{15})ne 1$ ,то не всякий эндоморфизм по некоторой подгрупе возможен. Т.е если рассмотреть и ,соответственно, , то этот эндоморфизм исключаем ? И т.д.

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

$begingroup$

Recently, I was reading on group operations and came across a question like determine the number of group homomorphism for two groups. I don’t specifically recall the example but how can one determine the number of homomorphism? Wouldn’t that depend on the order of the group? and bigger the order, more would be the no. of homomorphism. The example that I have in mind is rather simple, determine the number of homomorphism from $mathbb{Z_{8}}rightarrow mathbb{Z_{10}}$?

asked Nov 5, 2013 at 3:50

$endgroup$

$begingroup$

Figuring out the number of homomorphisms from a cyclic group is relatively easy; once you know what happens to the generator, you immediately know what everything else in the group is mapped to. All that remains from there is to check which of those give you a homomorphism.

In this case, the question we need to ask is if $f:mathbb{Z}_8 to mathbb{Z}_{10}$, what values of $f(1)$ could give us a homomorphism?

Keeping in mind that we need to have $8[f(1)]equiv 0pmod{10}$ (why?), the only valid choices are $f(1) equiv 5$ and $f(1) equiv 0$. You can verify that both of these define a valid homomorphism. Thus, there are two homomorphisms in this instance.

answered Nov 5, 2013 at 4:00

Ben GrossmannBen Grossmann

216k12 gold badges148 silver badges305 bronze badges

$endgroup$

$begingroup$

order of ${Z_8}=8$, order of ${Z_{10}}=10$. Both are finite cyclic groups. Hence, to check number of Homomorphism between them is gcd of their orders, $text{gcd}(8,10) = 2$, Hence the number of homomorphism function is $2$. This is not coincident.

One of The property of homomorphism states ${phi{(g^n)= (phi(g))^n}}$, such a homomorphism is completely specified by the image of 1. That is, if, 1 maps to a then x maps to xa.
Another property states that if ${|g|}$ is finite, then ${|phi(g)|}$ divides ${|g|}$, so ${|a|} ={1,2}$ as then ${a={0,5}}$, i.e., ${1 mapsto 0}$ or ${1 mapsto 5}$ .These are the only two homomorphism is possible.

answered Feb 20, 2021 at 13:41

SSASSA

3562 silver badges4 bronze badges

$endgroup$

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Определение.
Пусть

и

– группы. Отображение

называется гомоморфизмом, если для
любых

Определение.
Изоморфизмом
групп

называется гомоморфизм, который является
взаимно однозначным отображением. Если
группы

и

изоморфны,
то принято обозначать

.

При гомоморфизме
единица группы всегда переходит в
единицу. Действительно, если

– единицы групп

соответственно,
то

.
Умножив это равенство на

,
получим

.

Далее, при
гомоморфизме обратный к элементу

элемент переходит в обратный к

.
Действительно,

.
Аналогично,

Это и означает, что

Определение.
Пусть G
– группа с единицей e
и элемент

Наименьшее натуральное n,
для которого

называется
порядком элемента g
и обозначается o(g).
Если такого n
не существует, то считается, что

Если

–
гомоморфизм
групп, то порядки элементов
g
и f(g)
связаны, а
именно, если

то
n
делится на
m.
Действительно,

,
поэтому элемент f(g)
имеет конечный
порядок. Допустим, что n
не делится на m.
Тогда

,
где

В этом случае

что противоречит тому, что m
– наименьшая степень такая, что

Задача 1.4.1.
Определите
порядки всех элементов в следующих
группах а)

б)

в)

а)

В
группе

единицей
является элемент

Групповая операция – это сложение по
модулю 12. Порядок элемента x
это наименьшее натуральное n
такое, что

Например,

Поэтому порядок элемента

обзначаемый

равен
2. Порядки элементов

равны 3. Элементы

имеют четвертый порядок,

– шестой. Наконец, элементы

имеют двенадцатый порядок. Сам элемент

как и единица любой группы, имеет первый
порядок.

б), в) Решите
самостоятельно.

Пример 1. Покажем,
что

Каждому преобразованию группы

можно сопоставить перестановку –
перестановку вершин треугольника ABC.
Действительно,
занумеруем вершины: A
– 1, B
– 2, C
– 3. Тогда отображение

при котором

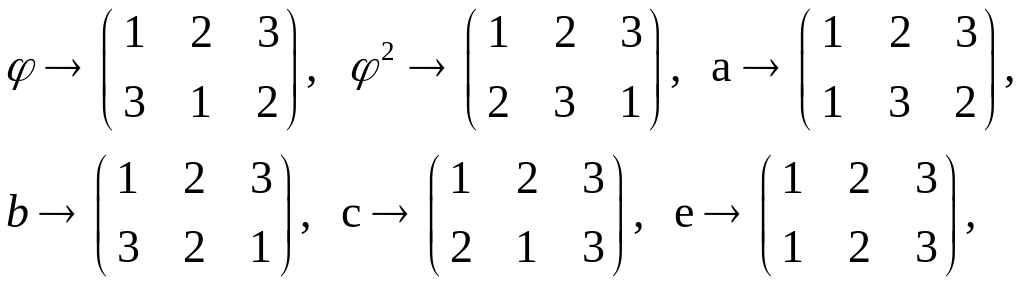
является изоморфизмом.

Пример 2.
Отображение

при котором каждому целому

ставится в соответствие его остаток

при делении на n
, является
гомоморфизмом групп, но не изоморфизмом.
Например, если

то

т.к.

Пример 3. Пусть

– группа всех действительных чисел
отличных от нуля с обычной операцией
умножения. Отображение

сопоставляет
каждой матрице ее определитель. Тогда
f
– гомоморфизм групп, т.к. определитель
произведения матриц равен произведению
определителей. Гомоморфизм f
не является
изоморфизмом, т.к. разные матрицы могут
иметь одинаковые определители.

Пример 4. Пусть

– группа всех действительных чисел с
операцией сложения, а

– группа всех положительных действительных
чисел с операцией умножения. Гомоморфизм

– определен формулой

Это действительно гомоморфизм, т.к.

Более того, этот гомоморфизм является
изоморфизмом.

Определение.
Пусть G
– группа. Нетрудно убедиться, что
множество всех изоморфизмов

также образует группу, которая называется
группой автоморфизмов группы G
и обозначается Aut
G.

Пример 5. Найдем
группу

Заметим, что в группе

каждый элемент

является суммой нескольких единиц:

Поэтому, чтобы задать гомоморфизм

достаточно задать

Действительно, если

то

и т.д.. Чтобы гомоморфизм был взаимно
однозначным отображением,

может равняться либо

либо

Обозначим первый автоморфизм

а второй –

Тогда

Поэтому

Ответы

1.4.1.б) Элементы

имеют
третий порядок, элементы a,b,c
– второй и
e
– первый;
в) элементы

имеют четвертый порядок, элемент (-1) –
второй и 1 – первый.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Гомоморфизмы групп и нормальные делители

Пусть заданы группы $mathcal{G}_1=(G_1,cdot,bold{1})$ и $mathcal{G}_2= (G_2,cdot,bold{1})$ . Отображение fcolon G_1to G_2 называют гомоморфизмом группы $mathcal{G}_1$ в группу $mathcal{G}_2$ (гомоморфизмом групп), если для любых x,yin G_1 выполняется равенство f(xcdot y)=f(x)cdot f(y) , т.е. образ произведения любых двух элементов группы $mathcal{G}_1$ при отображении равен произведению их образов в группе $mathcal{G}_2$ .

Если отображение сюръективно (биективно), то его называют эпиморфизмом (изоморфизмом) групп. В этом случае говорят также об эпиморфизме (изоморфизме) группы $mathcal{G}_1$ на группу $mathcal{G}_2$ .

Замечание 2.5. Мы обозначили операции групп $mathcal{G}_1$ и $mathcal{G}_2$ одинаково, как это обычно и делается для однотипных алгебр, хотя, конечно, это разные операции разных групп.

Пример 2.21. Пусть $mathcal{G}_1=(mathbb{Z},+,0)$ — аддитивная группа целых чисел, а $mathcal{G}_2=mathbb{Z}_{k}^{+}$ — аддитивная группа вычетов по модулю .

Зададим отображение так: для всякого целого га образ f(m) равен остатку от деления на . Можно проверить, что для любых целых и имеет место равенство $f(m+n)= f(m)oplus_{m}f(n)$ , т.е. для целых чисел остаток от деления суммы на равен сумме по модулю остатков от деления на каждого слагаемого.

Следовательно, данное отображение есть гомоморфизм группы $mathcal{G}_1$ в группу $mathcal{G}_2$ . Далее, поскольку любое целое число от 0 до k-1 есть остаток от деления на какого-то числа, то отображение является и эпиморфизмом группы $mathcal{G}_1$ на группу $mathcal{G}_2$ .

Теорема 2.14. Пусть $mathcal{G}_1,mathcal{G}_2$ — произвольные группы. Если $fcolonmathcal{G}_1to mathcal{G}_2$ — гомоморфизм, то:

1) образом единицы (нейтрального элемента) группы $mathcal{G}_1$ при отображении является единица группы $mathcal{G}_2$ , то есть f(bold{1})= bold{1} ;

2) для всякого элемента группы $mathcal{G}_1$ образом элемента $x^{-1}$ является элемент $[f(x)]^{-1}$ , обратный элементу f(x) , то есть $f(x^{-1})= [f(x)]^{-1}$ .

Согласно определению гомоморфизма, для произвольного xin G_1 имеем f(x)cdot f(bold{1})= f(xcdotbold{1}) . Далее, f(xcdotbold{1})=f(x) , то есть f(x)cdot f(bold{1})=f(x) . Следовательно, $f(bold{1})= (f(x))^{-1}cdot f(x)= bold{1}$ , то есть f(bold{1})=bold{1} .

Докажем второе утверждение теоремы. Используя определение гомоморфизма и уже доказанное первое утверждение теоремы, получаем

$f(x^{-1})cdot f(x)= f(x^{-1}cdot x)= f(bold{1})= bold{1}$ , то есть $f(x^{-1})= [f(x)]^{-1}$ .

Множество f(G_1) — образ носителя группы $mathcal{G}_1$ при гомоморфизме — замкнуто относительно умножения группы $mathcal{G}_2$ . Действительно, если $g_2,g'_2in f(mathcal{G}_1)$ , то существуют такие $g_1,g'_1in mathcal{G}_1$ , что f(g_1)=g_2 и f(g'_1)=g'_2 . Тогда

$g_2g'_2= f(g_1)f(g'_1)= f(g_1g'_1)in f(mathcal{G}_1).$

Из теоремы 2.14 следует, что $f(mathcal{G}_1)$ содержит единицу этой группы и вместе с каждым элементом обратный к нему элемент. Это значит, что можно определить подгруппу группы $mathcal{G}_2$ носителем которой будет множество $f(mathcal{G}_1)$ . Эту группу называют гомоморфным образом группы $mathcal{G}_1$ при гомоморфизме .

Группу mathcal{K} называют просто гомоморфным образом группы mathcal{G} , если существует гомоморфизм группы на группу . Так, группа $mathbb{Z}_{k}^{ast}$ при любом k>1 является гомоморфным образом аддитивной группы целых чисел (см. пример 2.21).

Пример 2.22. Рассмотрим мультипликативную группу (mathbb{C}setminus{0}, cdot,1) комплексных чисел с обычной операцией умножения комплексных чисел. Легко понять, что эта группа не что иное, как мультипликативная группа поля комплексных чисел.

Рассмотрим также группу $mathcal{M}_2$ невырожденных квадратных матриц второго порядка с операцией умножения матриц (см. пример 2.9.е).

Определим отображение множества mathbb{C} комплексных чисел в множество квадратных матриц второго порядка, положив для произвольного ненулевого комплексного числа a+bi , что

$f(a+bi)= begin{pmatrix}a&b\-b&aend{pmatrix}!.$

Покажем, что — гомоморфизм групп. С одной стороны,

$fbigl[(a+bi)cdot (c+di)bigr]= fbigl[(ac-bd)+i(ad+bc)bigr]= begin{pmatrix}ac-bd& ad+bc\ -ad-bc& ac-bd end{pmatrix}!.$

С другой стороны,

$f(a+bi)cdot f(c+di)= begin{pmatrix}a&b\ -b&aend{pmatrix}!cdot! begin{pmatrix} c&d\ -d&c end{pmatrix}= begin{pmatrix}ac-bd& ad+bc\ -ad-bc& ac-bd end{pmatrix}!.$

Следовательно,

fbigl[(a+bi)cdot (c+di)bigr]= f(a+bi)cdot f(c+di).

Таким образом, отображение — гомоморфизм групп, а гомоморфный образ мультипликативной группы комплексных чисел при — это подгруппа mathcal{K} группы матриц $mathcal{M}_2$ , состоящая из матриц вида $begin{pmatrix}a&b\ -b&aend{pmatrix}$ . Здесь мы учли, что любая матрица вида $begin{pmatrix}a&b\ -b&aend{pmatrix}$ является образом некоторого комплексного числа (а именно a+bi ) при отображении . Группа mathcal{K} — собственная подгруппа группы $mathcal{M}_2$ .

Важное свойство гомоморфизмов групп

Сформулируем без доказательства одно важное свойство гомоморфизмов групп.

Теорема 2.15. Если — гомоморфизм группы mathcal{G} в группу mathcal{K} , а — гомоморфизм группы в группу mathcal{L} , то композиция отображений fcirc g есть гомоморфизм группы в группу .

Рассмотрим некоторые свойства изоморфизмов групп.

Теорема 2.16. Если $fcolonmathcal{G}_1to mathcal{G}_2$ — изоморфизм группы $mathcal{G}_1$ на группу $mathcal{G}_2$ , то отображение $f^{-1}$ , обратное к отображению , есть изоморфизм группы $mathcal{G}_2$ на группу $mathcal{G}_1$ .

Пусть и — произвольные элементы группы $mathcal{G}_2$ , пусть также x=f(u) , а y=f(v) , где и {v} — элементы группы $mathcal{G}_1$ . Тогда

$f^{-1}(xy)= f^{-1}bigl(f(u)f(v)bigr)= f^{-1}(f(uv))= uv= f^{-1}(x)f^{-1}(y),$

т.е. отображение $f^{-1}$ — гомоморфизм второй группы в первую. Но так как отображение, обратное к биекции, есть биекция, то $f^{-1}$ — изоморфизм группы $mathcal{G}_2$ на группу $mathcal{G}_1$ .

Группы mathcal{G} и mathcal{K} называют изоморфными, если существует изоморфизм одной из них на другую. При этом используют обозначение mathcal{G}cong mathcal{K} .

Изоморфные группы с точки зрения их алгебраических свойств совершенно одинаковы, хотя их элементы могут иметь различную природу. Вернемся в этой связи к примеру 2.22. Легко убедиться в том, что определенное там отображение множества комплексных чисел на множество квадратных матриц специального вида является биекцией. Следовательно, мультипликативная группа комплексных чисел и группа матриц указанного вида с операцией умножения матриц изоморфны, хотя элементы этих групп на первый взгляд не имеют между собой ничего общего.

Определение 2.8. Ядром гомоморфизма группы mathcal{G} в группу mathcal{K} называют прообраз ker f единицы группы при гомоморфизме

$ker f=f^{-1}(bold{1})subset G,.$

Пример 2.23. Ядром гомоморфизма, рассмотренного в примере 2.21, служит множество всех целых чисел, делящихся на .

Теорема 2.17. Ядро ker f гомоморфизма fcolonmathcal{G}to mathcal{K} есть подгруппа группы .

Нужно убедиться в том, что множество ker f замкнуто относительно умножения группы mathcal{G} , содержит единицу этой группы и вместе с каждым элементом содержит обратный к нему элемент.

Если a,binker f , то есть f(a)=f(b)=bold{1} , то f(ab)= f(a)f(b)= bold{1} и abinker f . Ясно, что bold{1}inker f , так как f(bold{1})=bold{1} (см. теорему 2.14). Если ainker f , то

$f(a^{-1})= [f(a)]^{-1}= bold{1}^{-1}= bold{1}$ , то есть $a^{-1}inker f$ .

Ядро гомоморфизма, приведенного в примере 2.21, представляет собой подгруппу аддитивной группы целых чисел, состоящую из всех чисел, кратных .

Подгруппа mathcal{H} группы mathcal{G} называется нормальной подгруппой (нормальным делителем) группы , если aH=Ha для любого ain G .

В коммутативной группе, как было отмечено выше, aH=Ha . Следовательно, в этом случае любая подгруппа является нормальным делителем.

Пусть mathcal{H}=(H,cdot,bold{1}) — подгруппа группы mathcal{G}= (G,cdot, bold{1}) . Для фиксированных элементов a,bin G через aHb обозначим множество всех произведений вида ahb , где hin H . В силу ассоциативности групповой операции это обозначение корректно.

Теорема 2.18. Подгруппа mathcal{H}=(H,cdot,bold{1}) является нормальным делителем группы mathcal{G}=(G,cdot,bold{1}) тогда и только тогда, когда $aHa^{-1}subseteq H$ для любого ain G .

Если mathcal{H} — нормальный делитель, то для любого ain G имеем aH=Ha , т.е. для любого hin H найдется такое h_1in H , что ah=h_1a . Пусть элемент $xin aHa^{-1}$ , то есть $x=aha^{-1}$ для некоторого hin H . Так как ah=h_1a , то $x=h_1aa^{-1}=h_1in H$ и поэтому $aHa^{-1}subseteq H$ .

Обратно, если $aHa^{-1}subseteq H$ , то любой элемент $x=aha^{-1}$ , где hin H , принадлежит и множеству , то есть $aha^{-1}= h_1$ для некоторого h_1in H . Отсюда, умножая последнее равенство на справа, получим ah=h_1a , т.е. элемент из левого смежного класса принадлежит и правому смежному классу . Итак, aHsubseteq Ha .

Теперь возьмем для произвольного ain G обратный к элемент $a^{-1}$ и для него запишем включение $a^{-1}Hasubseteq H$ (напомним, что ( $(a^{-1})^{-1}=a$ ). Рассуждая как и выше, получим, что для некоторых h,h_1in H имеет место равенство $a^{-1}h=h_1a^{-1}$ , то есть ha=ah_1 и Ha subseteq aH . Итак, aH=Ha и mathcal{H} — нормальный делитель.

Связь между понятием нормального делителя и понятием гомоморфизма

Оказывается, существует связь между понятием нормального делителя и понятием гомоморфизма, которая продолжает и углубляет на новом уровне уже известную нам из первых лекций связь между понятиями отображения и класса эквивалентности.

Теорема 2.19. Ядро гомоморфизма группы mathcal{G} в группу mathcal{K} является нормальным делителем группы .

Для любого yinker f и любого ain G имеем

$f(aya^{-1})= f(a)f(y)f(a^{-1})= f(a)cdotbold{0}cdot f(a^{-1})= f(a) f(a^{-1})= bold{1},.$

Это значит, что для любого ain G выполняется соотношение $a(ker f)a^{-1}subseteqker f$ , а, согласно теореме 2.18, ker f — нормальный делитель.

Пусть mathcal{H}=(H,cdot,bold{1}) — нормальный делитель группы mathcal{G}= (G,cdot,bold{1}) . Рассмотрим множество всех левых смежных классов {aHcolon,ain G} . Это будет не что иное, как фактор-множество множества по определенному выше (см. теорему 2.11) отношению эквивалентности $sim_{H}$ .

Введем операцию умножения на множестве всех левых смежных классов следующим образом: произведением aHcdot bH классов и назовем класс abH .

Это определение корректно, так как множество aHcdot bH , т.е. множество всех произведений вида ahbh_1 для различных h,h_1in H , в силу того что Hb=bH для всякого bin G , совпадает с левым смежным классом abH . Действительно, поскольку hb=bh' для некоторого h'in H , то ahbh_1=abh'h_1in abH .

Теперь рассмотрим некоторый ain abH , т.е. x=abh для некоторого hin H_1 . Поскольку bh=h'b для некоторого h'in H , то x=ah'b= ah'bbold{1}in aHbH . Следовательно, aHcdot bH=abH .

Можно далее легко показать, что для каждого ain G имеют место

aHcdot H=Hcdot aH=aH и $aHcdot a^{-1}H= a^{-1}Hcdot aH=H$ .

Тем самым определена группа, носителем которой является фактор-множество $G/sim_{H}$ множества по отношению эквивалентности $sim_{H}$ с операцией умножения левых смежных классов, причем нейтральным элементом относительно этой операции служит носитель подгруппы mathcal{H} , а обратным к левому смежному классу будет левый смежный класс $a^{-1}H$ . Эту группу называют фактор-группой группы mathcal{G} по нормальному делителю и обозначают mathcal{G}/ mathcal{H} . Можно указать естественный гомоморфизм группы в фактор-группу mathcal{G}/mathcal{H} , который вводится согласно правилу: (forall cin G)(f(x)=xH) . Так как xHcdot yH= xyH , то для любых x,yin G имеем

f(xcdot y)= xyH= xHcdot yH= f(x)cdot f(y)

и — действительно гомоморфизм. Его называют каноническим гомоморфизмом группы mathcal{G} в фактор-группу mathcal{G}/mathcal{H} .

Пример 2.24. а. Рассмотрим аддитивную группу mathbb{R}= (mathbb{R},+,0) действительных чисел. Эта группа коммутативна. Напомним, что в коммутативной группе любая подгруппа будет нормальным делителем. Поэтому для нее нормальным делителем является подгруппа целых чисел mathbb{Z}= (mathbb{Z},+,0) (аддитивная группа целых чисел). (Для этих групп мы приняли такие же обозначения, как и для их носителей: mathbb{R} и соответственно.)

Выясним смысл отношения эквивалентности $sim_{mathbb{Z}}$ , определяемого через равенство левых смежных классов, по подгруппе в этом случае.

Равенство левых смежных классов a+mathbb{Z}= b+mathbb{Z} означает, что для любого целого найдется такое целое , что a+m=b+n , то есть a-b=n-min mathbb{Z} . Обратно, если разность a-b есть целое число, т.е. a-b=nin mathbb{Z} , то a+mathbb{Z}= (b+n)+mathbb{Z}= b+mathbb{Z} . Итак, $asim_{mathbb{Z}}b$ тогда и только тогда, когда a-bin mathbb{Z} , или, иначе говоря, действительные числа и эквивалентны по $sim_{mathbb{Z}}$ тогда и только тогда, когда их дробные части равны.

Аддитивная группа смежных классов, т.е. фактор-группа mathbb{R}/mathbb{Z} группы по нормальному делителю строится так: сумма классов a+mathbb{Z} и b+mathbb{Z} равна классу (a+b)+mathbb{Z} . Вводя обозначение a+mathbb{Z}=[a] , получаем [a]+[ b ]=[a+b] . При этом [0]=mathbb{Z} (т.е. единица фактор-группы — это смежный класс нуля — множество всех целых чисел), причем -[a]=[-a]=(-a)+mathbb{Z} . Обратим внимание на то, что смежный класс числа однозначно определяется его дробной частью <x> (см. пример 1.14.6), то есть [x]=[<x>] . Канонический гомоморфизм в данном случае задается так: xmapsto[x] .

б. Рассмотрим теперь аддитивную группу действительных чисел по модулю 1, т.е. группу $mathbf{S}^1=([0;1),oplus_{1},0)$ , заданную на полуинтервале [0;1) , сложение в которой определяется так: $xoplus_{1}y=<x+y>$ (дробная часть суммы x+y ). Другими словами,

$xoplus_{1}y= begin{cases}x+y,& text{if}quad x+y leqslant 1;\ x+y-1,& text{if}quad x+y geqslant 1.end{cases}$

Докажем, что группа $mathbf{S}^1$ изоморфна фактор-группе mathbb{R}/ mathbb{Z} , то есть $mathbb{R}/mathbb{Z}congmathbf{S}^1$ .

Зададим отображение varphi множества {[a]colon, ain mathbb{R}} смежных классов в полуинтервал [0;1) так, что varphi([x])=<x> . Поскольку [x]=[<x>] , то varphi — биекция и, кроме того,

$varphibigl([x]+[y]bigr)= varphibigl([x+y]bigr)= <x+y>= <<x>+<y>>= <x>oplus_{1}<y>= varphi([x])oplus_{1}varphi([y]).$

Это значит, что varphi — изоморфизм mathbb{R}/ mathbb{Z} на $mathbf{S}^1$ .

Группу $mathbf{S}^1$ можно воспринимать как «наглядный образ» фактор-группы mathbb{R}/ mathbb{Z} . Довольно абстрактная идея фактор-группы кристаллизуется в виде группы с носителем [0;1) и операцией сложения неотрицательных действительных чисел, строго меньших единицы, с отбрасыванием в результате целой части. Здесь хорошо видна «польза» понятия изоморфизма. То, что само по себе не очень наглядно, становится наглядным через свой изоморфный образ.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Правила форума

Кто сейчас на конференции

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged .

Гомоморфизмы групп и нормальные делители

Важное свойство гомоморфизмов групп

Связь между понятием нормального делителя и понятием гомоморфизма

Не пропустите также:

Not the answer you’re looking for? Browse other questions tagged

.