Как найти количество единиц в двоичной записи - AvtoShod.ru

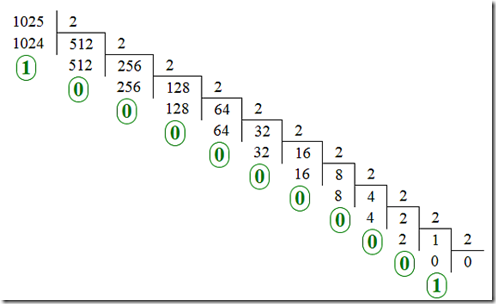
Данная задачка судя по всему типовая в ЕГЭ по информатике, алгоритм ее решения в общем случае следующий: перевести число в двоичную форму (например, тут — http://floatingpoint.ru/online/dec2bin.php) и подсчитать количество единиц — калькулятор нулей и единиц в двоичной записи числа

Однако в некоторых простых случаях можно попробовать разложить искомое число на сумму или разность степеней двоек, и проделать вычисления в уме.

Для этого нужно помнить несколько первых степеней двойки и двоичные записи по крайней мере некоторых чисел от 1 до 15:

1024 = 2^10, 512 = 2^9, 256 = 2^8, 128 = 2^7, 64 = 2^6, 32 = 2^5, 16 = 2^4

15 = 1111, 14 = 1110, 13 = 1101, 12 = 1100, 11 = 1011, 10 = 1010, 9 = 1001, 8 = 1000, 7 = 111, 6 = 110, 5 = 101, 4 = 100, 3 = 11, 2 = 10, 1 = 1.

Так же могут оказаться полезны некоторые суммы, например:

192 = 128 + 64

160 = 128 + 32

320 = 256 + 64

640 = 512 + 128

Приведем некоторые типовые примеры.

Сколько единиц в двоичной записи числа 1025?

1025 = 1024 + 1
1024 = 2^10 это степень двойки, а единица так и будет единицей, следовательно, 
всего в двоичной записи числа 1025 ровно 2 единицы.

10000000001

Сколько единиц в двоичной записи числа 519?

519 = 512 + 7
512 = 2^9 это степень двойки, а 7 записывается в двоичной системе как 111 и содержит три единицы, 
следовательно, всего в двоичной записи числа 519 содержится ровно 4 единицы.

1000000111

Сколько единиц в двоичной записи числа 514?

514 = 512 + 2
Слагаемые 512 = 2^9 и 2 = 2^1 - это степени двойки, следовательно, в двоичной записи числа 514 
ровно 2 единицы.

1000000010

Сколько единиц в двоичной записи числа 127?

127 = 128 - 1
Число 128 представляет собой целую степень двойки и равняется 2^7, требуя таким образом 
для своей записи ровно 8 бит: 10000000
10000000-1 = 1111111
Следовательно, в записи числа 127 содержится 7 единиц.

1111111

Сколько единиц в двоичной записи числа 195?

195 = 192 + 3 = 128 + 64 + 3
128 = 2^7
64 = 2^6
3 = 11 в двоичной системе и содержит 2 единицы. Таким образом в двоичной записи числа 195 
содержится 4 единицы.

11000011

Сколько единиц в двоичной записи числа 173?

173 = 160 + 13
160 = 128 + 32 = 2^7 + 2^5, а 13 = 1101 в двоичной системе. 
Тогда всего получим 5 единиц.

10101101

Сколько единиц в двоичной записи числа 3458?

3458 = 2048 + 1410
1410 = 1024 + 386
386 = 256 + 130
130 = 128 + 2
Таким образом 3458 = 2^11 + 2^10 + 2^8 + 2^7 + 2^1 и всего будет 5 единиц.

110110000010

Источник

Самый эффективный метод следующий: пока число (его надо интерпретировать как беззнаковое число, чтобы подсчитать все единицы), допустим n, не равно нулю выполнить следующую операцию

n &= n - 1;

и соответственно увеличить счетчик единиц на единицу.

Принцип следующий. Допустим в числе имеется одна 1

0b00100000

Если из этого числа вычесть 1, то получится

0b00011111

Теперь если применить бинарную операцию И, то получим

0b00100000
&
0b00011111
==========
0b00000000

Число стало равным 0, следовательно оно содержало только одну 1, так как данная операция была проделана только один раз.

Используя же те методы, которые вы указали, то придется сдвигать либо само число, либо единицу 6 раз, чтобы добраться до единицы в исходном числе, и 6 раз придется выполнить сравнение с единицей. А таблица просмотра совершенно не применима для чисел, которые занимают более одного байта. Тем более она еще занимает место в памяти для такой простой задачи.

Источник

DeaZZZlee

1 / 1 / 0

Регистрация: 23.02.2020

Сообщений: 24

Сколько единиц в бинарной записи?[РЕШЕНИЕ]

27.04.2020, 13:42. Показов 35169. Ответов 8

Метки python, python 3.7 (Все метки)

Сколько 1 в бинарной записи числа
Найти, сколько единиц содержит бинарная запись числа.

Входные данные: Целое неотрицательное число K.

Выходные данные: Сколько единиц содержит бинарная запись числа.

Примеры

Вход
5

Выход
2

Решение:

Python

x = int(input())
y = []
repeatValue = 0
while x >0: #подобие перевода в двоичную систему и пополнение значения в массив
    y.append(x%2)
    x//=2
    if x == 0:
        y.append(x%2)
        break
for k in range(len(y)): #нахождение кол-ва единиц
    if y[k] == 1:
        repeatValue+=1  
print(repeatValue)

Доработайте,если кому интересно или кто ищет — возьмите.

u235

4383 / 2492 / 526

Регистрация: 07.11.2019

Сообщений: 4,137

27.04.2020, 17:15

Python

1 2	x = int(input()) print(bin(x).count('1'))

1 / 1 / 0

Регистрация: 23.02.2020

Сообщений: 24

27.04.2020, 17:49

[ТС]

Так раздел вроде для начинающих,типо подобный сахар новичкам вроде как ни к чему.

5889 / 3347 / 1033

Регистрация: 03.11.2009

Сообщений: 9,974

27.04.2020, 17:57

потому что

u235

27.04.2020, 19:29

Не по теме:

Jabbson, это же про Форт.

1728 / 967 / 199

Регистрация: 22.02.2018

Сообщений: 2,694

Записей в блоге: 6

27.04.2020, 21:57

Сообщение от DeaZZZlee

Так раздел вроде для начинающих,типо подобный сахар новичкам вроде как ни к чему

Так это задача и вариант ее решения, который дал u235, для новичков. Функции bin и count это все из базовых знаний необходимых новичкам.
А Ваше решение из серии как простую задачу превратить в сложную.

5889 / 3347 / 1033

Регистрация: 03.11.2009

Сообщений: 9,974

27.04.2020, 22:04

Сообщение от Viktorrus

А Ваше решение из серии как простую задачу превратить в сложную.

или ‘как решить задачу на си, используя синтаксис питона’

iSmokeJC

Am I evil? Yes, I am!

16124 / 9007 / 2605

Регистрация: 21.10.2017

Сообщений: 20,712

27.04.2020, 22:20

Jabbson, не! Как решить задачу питона, использовав синтаксис си. Бугаг

Python

n = int(input())
count = 0
while n > 0:
    count += n & 1
    n >>= 1
print(count)

flash_back

20 / 20 / 20

Регистрация: 07.02.2016

Сообщений: 87

11.02.2021, 11:54

Python

x = int(input())
count = 0
while x:
   x, a = divmod(x, 2)
   count += a
print(count)

IT_Exp

Эксперт

87844 / 49110 / 22898

Регистрация: 17.06.2006

Сообщений: 92,604

11.02.2021, 11:54

Помогаю со студенческими работами здесь

Посчитать сколько единиц есть в записи числа в двоичной системе счисления
Дано число N в десятичной системе счисления. Нужно посчитать сколько единиц есть в записи этого…

Число X перевели из десятичной в двоичную систему счисления.Сколько единиц получилось в двоичной записи числа?
(32^32+16^16-1)*8^8+4^4-1=X
Число X перевели из десятичной в двоичную систему счисления.Сколько…

Найти следующее число, в двоичной записи которого столько же единиц, сколько и в двоичном представлении числа N
Найти следующее число, в двоичной записи которого столько же единиц, сколько и в двоичном…

[NASM] Определить, в каком из трёх чисел единиц больше единиц в двоичной записи
Дано 3 числа в двоичной системе счисления. Определить, в каком числе число единиц больше. NASM…

Определить количество единиц в цифровой записи числа, кроме единиц в младших разрядах
Ребят,помогите,срочно надо! Сам что-то не понимаю(
Дано натуральное число N. Определить…

После бинарной записи файл всё равно остаётся пустым
Хочу организовать в программе запись во внешний файл, чтобы хранить данные, при необходимости…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Решение задач 1 ЕГЭ по информатике 2015 года

Рассмотрим задачу №1 из демоверсии ФИПИ 2015 года:

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110.Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) для буквы В – 101
2) это невозможно
3) для буквы В – 010
4) для буквы Б – 10

Давайте проанализируем текст задачи. Итак, нам известно, что используется неравномерный двоичный код. Что это такое? На самом деле все очень просто:

равномерное кодирование — каждый символ кодируется кодами равной длины

неравномерное кодирование — разные символы могут кодироваться кодами разной длины

Например, если у нас есть три символа А, Б, В и закодированы они так:

А — 010
Б — 011
В — 111

, то это равномерное кодирование, так как длина кода одинаковая. Если же эти же символы мы закодируем вот так:

А — 01
Б — 110
В — 1011

, то получим неравномерное кодирование.

Кроме этого, нам необходимо знать и понимать условие Фано

Никакое кодовое слово не может быть началом другого кодового слова

Также существует обратное условие Фано

Никакое кодовое слово не является окончанием другого кодового слова

Чтобы однозначно декодировать сообщение, достаточно того, чтобы условие Фано (или обратное условие) выполнялось.

Теперь, получив необходимые знания, можем перейти к решению задачи.

Рассмотрим первый вариант ответа. Если мы для буквы В сократим код до 101, то условие Фано нарушено не будет. Действительно, с кода 101 не начинается ни один из четырех оставшихся кодов для А, Б, Г и Д и все коды различны.

Второй вариант отпадает, так как мы только что убедились, что это возможно.

Третий вариант не подходит, так как в этом случае код буквы В — 010 будет начинаться с 0, а 0 — это код буквы А. Получается, что это нарушает условие Фано.

Вариант 4 тоже не подходит. В этом случае код буквы Б — 10 будет являться началом для кода буквы В, а это нарушение условия Фано.

Правильный ответ: 1.

Для успешного решения задач типа А1 ЕГЭ по информатике рекомендую ознакомиться со статьями “Системы счисления” и “Перевод чисел из двоичной системы счисления в десятичную”. Для контроля правильности перевода удобно использовать “Скрипт для перевода числа из десятичной системы счисления в любую другую”.

Задачи А1 предполагают проверку знаний о системах счисления и двоичном представлении информации в памяти компьютера.

Рассмотрим решение задачи А1 из демоверсии ЕГЭ 2012.

Сколько единиц в двоичной записи числа 1025?
1)   1
2)   2
3)   10
4)   11

Данную задачу можно решить простым переводом числа 1025 в двоичную систему счисления, а затем посчитать количество единиц.

Как видно, в полученном двоичном числе содержится 2 единицы.

Второй способ решения данной задачи рассчитан на тех, кто хорошо знает степени числа 2. Если посмотреть на число 1025 внимательно, можно заметить, что 1025=1024+1. Число 1024 – это 2¹⁰. Отсюда следует, что 1025=2¹⁰+1.

Если посмотреть как выглядят степени числа 2 записанные в двоичной системе счисления, то нетрудно представить число 1024 в двоичной системе счисления.

2¹=2₁₀=10₂

2²=4₁₀=100₂

2³=8₁₀=1000₂

2⁴=16₁₀=10000₂

2⁵=32₁₀=100000₂

…

2¹⁰=1024₁₀=10000000000₂

Прибавив к получившемуся числу единицу получим число 10000000001₂, которое содержит 2 единицы.

Третий способ вытекает из предыдущего. Если посмотреть внимательно, то можно увидеть, что любое число, являющееся степенью двойки и записанное в двоичной системе счисления содержит одну единицу. Таким образом узнать количество единиц в двоичной записи любого числа очень просто — достаточно представить его как сумму степеней числа 2 — количество слагаемых и будет указывать число единиц.

Возьмем для примера число 73 и узнаем сколько единиц в его двоичной записи.

73=64+8+1=2⁶+2³+2⁰. Так как слагаемых у нас получилось три, значит и единиц в двоичной записи числа 73 будет тоже 3.

Решение задачи А1 демонстрационной версии ЕГЭ 2013:

Сколько единиц в двоичной записи десятичного числа 255?

1) 1 2) 2 3) 7 4) 8

Первый способ:

Для успешного решения данной задачи необходимо знать, что 256 это 2 в восьмой степени или 10000 0000в двоичной системе счисления — 256=2⁸=100000000₂. Соответственно, 255 — это 11111111в двоичной системе счисления — 255₁₀=11111111₂. Правильный ответ — 4 (8 единиц).

Второй способ:

Этот способ заключается в переводе числа 255 из десятичной системы счисления в двоичную и подсчете единиц:

Как видим, количество единиц восемь. Правильный ответ 4.

Автор:

Источник

How do you count the number of ones in a given integer’s binary representation.

Say you are given a number 20, which is 10100 in binary, so number of ones is 2.

jamylak

128k30 gold badges230 silver badges230 bronze badges

asked Mar 21, 2013 at 6:24

What you’re looking for is called the Hamming weight, and there are a lot of algorithms to do it. Here’s another straightforward one:

def ones(n):
    w = 0
    while (n):
        w += 1
        n &= n - 1
    return w

answered Mar 21, 2013 at 6:31

CairnarvonCairnarvon

25.6k9 gold badges51 silver badges65 bronze badges

Use the awesome collections module.

>>> from collections import Counter
>>> binary = bin(20)[2:]
>>> Counter(binary)
Counter({'0': 3, '1': 2})

Or you can use the built-in function count():

>>> binary = bin(20)[2:]
>>> binary.count('1')
2

Or even:

>>> sum(1 for i in bin(20)[2:] if i == '1')
2

But that last solution is slower than using count()

answered Mar 21, 2013 at 6:27

TerryATerryA

58.6k11 gold badges114 silver badges142 bronze badges

>>> num = 20
>>> bin(num)[2:].count('1')
2

answered Mar 21, 2013 at 6:28

YarkeeYarkee

8,9265 gold badges28 silver badges29 bronze badges

The usual way to make this blinding fast is to use lookup tables:

table = [bin(i)[2:].count('1') for i in range(256)]

def pop_count(n):
   cnt = 0
   while n > 0:
     cnt += table[n & 255]
     n >>= 8
   return cnt

In Python, any solution using bin and list.count will be faster, but this is nice if you want to write it in assembler.

vvvvv

23.8k19 gold badges48 silver badges75 bronze badges

answered Mar 21, 2013 at 6:37

Torsten MarekTorsten Marek

83k21 gold badges91 silver badges98 bronze badges

The int type has a new method int.bit_count() since python 3.10a, returning the number of ones in the binary expansion of a given integer, also known as the population count as follows:

n = 20
bin(n)
'0b10100'

n.bit_count() returns 2 as it has 2 ones in the binary representation.

answered Sep 19, 2020 at 19:04

HamzaHamza

5,2353 gold badges27 silver badges42 bronze badges

The str.count method and bin function make short work of this little challenge:

>>> def ones(x):
        "Count the number of ones in an integer's binary representation"
        return bin(x).count('1')

>>> ones(20)
2

answered Mar 21, 2013 at 6:29

Raymond HettingerRaymond Hettinger

214k62 gold badges378 silver badges481 bronze badges

You can do this using bit shifting >> and bitwise and & to inspect the least significant bit, like this:

def count_ones(x):
    result = 0
    while x > 0:
        result += x & 1
        x = x >> 1
    return result

This works by shifting the bits right until the value becomes zero, counting the number of times the least significant bit is 1 along the way.

answered Jan 29, 2020 at 16:00

I am a new coder and I found this one logic simple. Might be easier for newbies to understand.

def onesInDecimal(n):
  count = 0
  while(n!=0):
    if (n%2!=0):
        count = count+1
        n = n-1
        n = n/2
    else:
        n = n/2
  return count

answered Jun 24, 2017 at 13:22

For a special case when you need to check quickly whether the binary form of the integer x has only a single 1 (and thus is a power of 2), you can use this check:

if x == -(x | (-x)):
    ...

The expression -(x | (-x)) is the number that you get if you replace all 1s except the last one (the least significant bit) in the binary representation of x with 0.

Example:

12 = 1100 in binary

-12 = …110100 in binary (with an infinite number of leading 1s)

12 | (-12) = …111100 in binary (with an infinite number of leading 1s)

-(12 | (-12)) = 100 in binary

answered Dec 27, 2021 at 23:35

If the input number is ‘number’

number =20
len(bin(number)[2:].replace('0',''))

Another solution is

from collections import Counter

Counter(list(bin(number))[2:])['1']

Источник

Сколько единиц в двоичной записи числа 1025?

Сколько единиц в двоичной записи числа 519?

Сколько единиц в двоичной записи числа 514?

Сколько единиц в двоичной записи числа 127?

Сколько единиц в двоичной записи числа 195?

Сколько единиц в двоичной записи числа 173?

Сколько единиц в двоичной записи числа 3458?

Сколько единиц в бинарной записи?[РЕШЕНИЕ]

Решение задач 1 ЕГЭ по информатике 2015 года

Решение задачи А1 демонстрационной версии ЕГЭ 2013:

Не пропустите также: