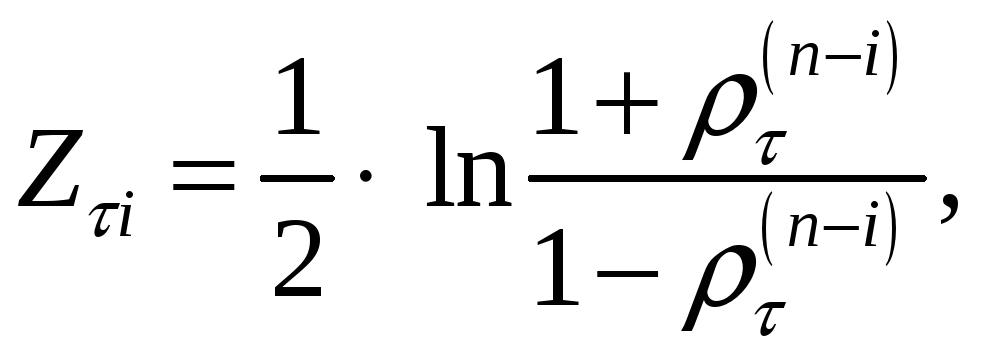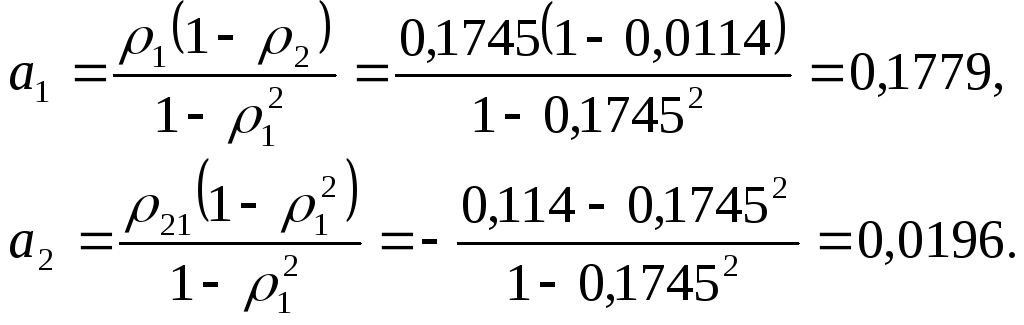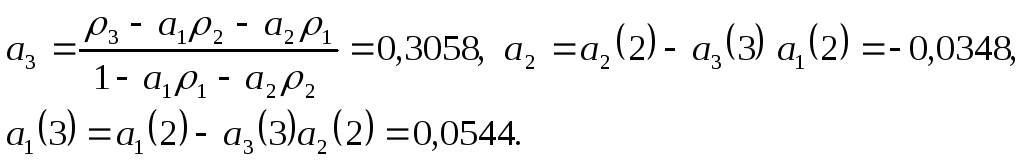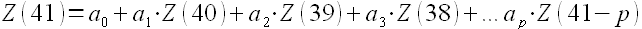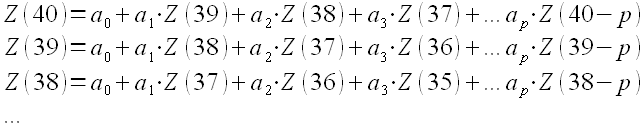В основе метода
прогнозирования с использованием
авторегрессионых моделей лежит гипотеза
о стационарности изучаемого явления,
т.е. о сохранении статистических
характеристик явления без изменения
на ретроспективном промежутке времени,
в настоящем и будущем.
При
прогнозировании важен выбор модели
авторегрессии наименьшего порядка с
целью обеспечения требуемой точности
описания данных.
При
использовании модели авторегрессии
порядка p
нужно проверить существенность
автокорреляции остатков в этой модели,
применив критерий Дарбина-Уотсона.
Затем проверяется условие нормальности
распределения случайной компоненты
путем исследования показателей асимметрии
и эксцесса
,
а также их средних квадратичных ошибок
и
Итак,
прежде чем использовать при прогнозировании
авторегрессионую моделью, нужно убедиться
в следующем.
1.
Случайная компонента динамического
ряда представляет собой стационарности
в широком смысле случайный процесс. Для
определения ее стационарности находят
значения автокорреляционной функции
для случайной компоненты, используя
уровней динамического ряда. В результате
получают
групп коэффициентов автокорреляции, в
каждую из которых будет входить k+1
коэффициентов. Затем, используя z
—
критерий Фишера, устанавливают
однородность коэффициентов автокорреляции,
входящих в одну и ту же группу. Если
гипотеза об однородности не отвергается
для всех групп, можно сделать вывод о
том, что отклонения
представляют собой стационарный в
широком смысле случайный процесс.
2.
Случайная компонента
является случайной величиной, не
зависящей от времени.
3.
Отклонения от расчетных значений,
полученных по авторегрессионой модели,
являются выборкой нормально распределенной
случайной величины с математическим
ожиданием, равным нулю.
4.
Отклонения от расчетных значений,
полученных по авторегрессионой модели,
не содержат автокорреляции.
Если
при проверке установлено, что для
динамического ряда не выполняется хотя
бы одно из перечисленных выше условий,
то авторегрессионая модель не применяется
для описания исследуемого динамического
ряда.
Установив
выполнимость указанных условий, вычисляют
коэффициенты авторегрессионой модели
и определяют, насколько точно можно
оценить эти коэффициенты по имеющейся
выборке.
Оценки
коэффициентов авторегрессии
являются случайными
величины со средними, равными, и
дисперсиями, вычисляемыми по формулам
,
где
— i-и
диагональный элемент матрицы, обратной
матрице системы нормальных уравнений
для определения коэффициентов
Величина
имеет t-распределение
Стьюдента с
степенями свободы.
После
вычисления коэффициентов авторегрессионой
модели прогнозируют значения
на период
по авторегрессионой модели следующим
образом.
Сначала
вычисляют значение
по формуле
.
Вычисленное
значение
подставляют в модель
и
находят значение
и т.д.
Важную
роль играет оценка погрешности прогноза,
полученного с помощью авторегрессионой
модели. Для построения доверительного
интервала прогноза используется тот
факт, что остатки
в уравнении авторегрессии распределены
нормально с нулевым математическим
ожиданием и дисперсией
.
Если коэффициенты авторегрессионой
модели известны из других выборок или
из априорных соображений, то оценка
дисперсии случайной величины
вычисляется по формуле
где n
— число уровней динамического ряда; h
— порядок авторегрессионой модели.
Случайная
величина
имеет
t
— распределение Стьюдента
степенями свободы. Тогда вероятность
того, что величина
не превосходит, можно определить по
формуле
,
откуда следует, что
или
,
где
— истинное значение исследуемого
параметра,
— предсказанное значение.
Если
же коэффициенты авторегрессионой модели
вычислены на основании исследуемого
динамического ряда, то оценка дисперсии
остатков
вычисляется по формуле
где
— дисперсия динамического ряда
— i-й
коэффициент авторегрессии;
— коэффициент автокорреляции i-го
порядка.
Доверительный
интервал прогноза будет аналогичным:
.
Пример 9.8.
Рассмотрим динамический ряд, характеризующий
объем производства фирмы “Эврика”
(табл.9.10).
Таблица
9.10
|
Год |
Объем |
Год |
Объем |
Год |
Объем |
||
|
1976
1977
1978
1979
1980 |
Для
описания тренда данного ряда динамики
выберем линейную функцию
.
Решив систему нормальных уравнений
получим:
Тогда уравнение тренда будет иметь вид:
(9.18)
Проверим выполнимость
предпосылок возможности использования
авторегрессионых моделей для
прогнозирования.
Прежде всего
проверим гипотезу о случайном характере
отклонений от тренда с помощью критерия
серий:
Динамический
ряд остатков представлен в табл.9.11.
Таблица
9.11.
|
|
|
|
|
|
|
|
1 2 3 4 5 |
-28,002 -24,463 — 24,919 32,625 26,169 |
6 7 8 9 10 |
-6,287 4,257 8,801 -6,655 19,889 |
11 12 13 14 15 |
24,433 57,977 4,521 10,065 -98,391 |
Построив
вариационный ряд -98,391; -28,002; -24,919; -24,463;
-6,655; -6,287; 4,257; 4,521; 8,801; 10,065; 19,889; 24,433; 26,169;
32,625; 57,977, определим медиану Me
= 4,521 и образуем последовательность из
плюсов и минусов по следующему правилу.
На i—м
месте ставим плюс, если i-й
уровень динамического ряда остатков
превосходит медиану, и минус, если он
меньше медианы. Получим последовательность
знаков:
-,
-, -, +, +, -, -, +, -, +, +, +, +, -.
Отсюда
найдем протяженность самой длинной
серии
и общее число серий
.
Тогда из неравенств
следует, что
отклонения от тренда носят случайный
характер.
Далее
проверяем гипотезу о том, что случайная
компонента представляет собой стационарный
случайный процесс. Для этого находим
значения автокорреляционной функции
соответственно для n
= 15,14,13,12 уровней динамического ряда,
т.е. из расчетов последовательно
исключаются первый, второй, третий и
четвертый уровни. Большее число уровней
исключать нецелесообразно, так как ряд
отклонений слишком короток. Для всех
значений коэффициентов автокорреляции
вычислены значения z—
критерия Фишера:
средние
для каждой группы
и величина
для
каждого сдвига
.
Результаты расчетов приведены в
табл.9.12.
Таблица
9.12
|
Кол-во уровней |
|
Сдвиг |
|||
|
1 |
2 |
3 |
4 |
||
|
15 |
|
0,1745 0,1763 |
0,0114 0,0114 |
-0,2908 -0,2994 |
-0,1076 -0,1080 |
|
14 |
|
0,0988 0,0991 |
-0,0965 -0,0968 |
-0,6156 -0,7179 |
-0,0227 -0,0227 |
|
13 |
|
-0,0060 -0,0060 |
0,0013 0,0013 |
-0,5605 -0,6336 |
-0,2387 -0,2434 |
|
12 |
|
0,1287 0,1396 |
0,1303 0,1311 |
-0,7899 -1,0712 |
-0,3477 -0,3628 |
|
|
0,10225 0,2047 |
0,01175 0,2352 |
-0,68052 2,1104 |
-0,18422 0,3365 |
Вычисленные
значения
,
представленные в последней строке
табл.9.12, сравниваем с квантилем
-распределения
для уровня значимости
и числа степеней свободы
,
т.е. с
.
Из таблицы видим, что фактические
значения
меньше . Следовательно, гипотеза об
однородности коэффициентов автокорреляции
для каждого сдвига не отвергаются и
отклонения от линейного тренда являются
стационарным в широком смысле случайным
процессом.
Для
выбора порядка авторегрессионой модели
рассмотрим значения автокорреляцио
ной функции, представленные в табл.9.13,
и построим коррелограмму (рис.9.2).
Таблица
9.13
|
Сдвиг |
1 |
|
Значение |
0,1745 |
0,0706
0,0412
-0,0775
-0,1076
-0,2908
Рис.9.2
На
рис. 9.2 видно, что, начиная с третьего
сдвига, происходит затухание коррелограммы,
т.е. связь с прошлым ослабевает. Это
свидетельствует о том, что нужно строить
авторегрессионые модели не выше третьего
порядка. Так как для отклонений от
линейного тренда автокорреляционная
функция достигает наибольшего значения
на первом сдвиге, то строим три модели
соответственно 1-го, 2-го и 3-го порядков:
Единственный
коэффициент модели первого порядка
равен коэффициенту автокорреляции
первого порядка:
Коэффициенты авторегрессионой модели
второго порядка находим из соотношений:
Используя
коэффициенты
и
модели авторегрессии второго порядка
и коэффициенты автокорреляции
находим коэффициенты модели третьего
порядка:
Применим
критерий Бартлетта для определения
порядка авторегрессионой модели. Для
этого вычислим сумму квадратов остатков
для моделей:
Значения критерия
Бартлетта для сравнения моделей первого
и второго, первого и третьего, второго
и третьего порядков соответственно
равны:
Табличные
значения
для уровня значимости
и
и
степени свободы равны:
Следовательно,
гипотеза о том, что авторегрессионые
модели второго и третьего порядков
дадут лучшие результаты, отвергается,
т.е. для прогнозирования можно применять
авторегрессионую модель первого порядка.
Этот вывод подтверждается и сравнением
финальных ошибок прогноза на текущий
момент времени:
ФОП
где
ФОП
Для выбранной
авторегрессионой модели первого порядка
проверим существенность автокорреляции
остатков, пользуясь критерием
Дабрина-Уотсона. Для рассматриваемого
примера
Так
как при уровне значимости
выполняется неравенство
,
т.е. 1,2,3,<1,3550<2,77, то с вероятностью
=0,975
можно утверждать, что автокорреляция
в отклонениях от авторегрессионой
модели первого порядка отсутствует.
Проверим
условие нормальности распределения
величины
,
используя показатели асимметрии и
эксцесса:
и средние квадратичные
ошибки коэффициентов асимметрии и
эксцесса:
Из значений
асимметрии и эксцесса и их ошибок
следует, что неравенства
не выполняются,
т.е. отклонения от авторегрессионой
модели первого порядка не подчиняются
нормальному закону распределения.
Учитывая результаты
проверок основных предпосылок, делаем
вывод о том, что отклонения от линейного
тренда могут быть аппроксимированы
авторегрессионой моделью
(9.19)
Из
уравнения тренда (9.18) выразим случайную
компоненту
и
подставим это значение в авторегрессионую
модель (9.19) первого порядка:
в результате
преобразований получим следующую модель
прогноза объема производства фирмы
“Эврика”:
Прогноз объема
производства на 1991 г. по этой модели
Доверительный
интервал прогноза построить нельзя,
так как вероятностные оценки прогноза
предполагают нормальное распределение
случайной величины
,
что для рассматриваемого примера не
подтверждается.
Проверка
условий 1—4, приведенных в начале
параграфа, для данного примера показал,
что не выполняется условие 3. Это означает,
что рассматриваемый процесс может
описываться авторегрессией более
высокого порядка. Такой вывод можно
сделать, и рассматривая табл. 9.13 значений
автокорреляционной функции.
Таким
образом, оценка порядка авторегрессионой
модели являются очень “тонким” вопросом.
Определяя порядок авторегрессионой
модели, нужно учитывать внутреннюю
структуру экономических процессов за
прошлые периоды времени. Небольшое
число уровней динамического ряда также
сказывается при выборе порядка
авторегрессионой модели.
Некоторую помощь
в решении этого вопроса может оказать
исследование конкретных процессов
авторегрессии, которым соответствуют
авторегрессионые модели различного
порядка. Тогда возможный порядок
авторегрессии можно оценить путем
сопоставления с некоторыми стандартными
моделями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 3 мин. Просмотров 1.9k. Опубликовано 29.08.2010
В данной статье мы разберем пример прогнозирования курса акций Лукойла с помощью авторегрессионной модели. Эта модель так же называется AR (AutoRegressive ). Эта модель используется во многих финансовых отраслях, где необходимо прогнозировать различные данные, например, прогнозирование значений ВВП, объема продаж товаров на предприятии, стоимости ценных бумаг и т.д. AR относится к классу регрессионных методов. Рассмотрим авторегрессию первого порядка AR(1), которая характеризует тесноту связи между соседними значениями ценового или иного ряда.
Авторегрессионная модель первого порядка имеет следующую формулу:
Yi=α+β*Yi-1+ε
β,α – коэффициенты авторегрессии;
ε– белый шум, независимая случайная величина;
Yi-1 – предыдущее значение временного ряда;
Yi – текущее значения временного ряда.
Для того что бы сделать прогноз на основе этой модели воспользуемся программой MS Excel. И так, давайте спрогнозируем стоимость акций Лукойла (LKOH) на несколько периодов вперед. Построение авторегрессии имеет схожий алгоритм с автокорреляцией. Дневные котировки акции взяты за один месяц с 31 июля 2010г. по 31 августа 2010г. Следует заметить, что взята ценная бумага, торгуемая на бирже ММВБ.
Для начала экспортируем котировки с сайта finam.ru за выбранный период. Всего получилось 21 значение котировки. Экспорт в Excel будет выглядеть следующим образом.

График ценной бумаги представляет собой ярко выраженный линейный тренд.

Сделаем прогноз этой ценной бумаги на следующие три периода, то есть на 3 дня вперед. Для этого необходимо найти авторегрессию нашего ценового ряда, то есть тесноту связи между соседними членами ценового ряда. Скопируем со сдвигом в одну ячейку наш временной ряд и вставим его в столбец “D”.

Далее, рассчитаем коэффициенты авторегрессии для ценового ряда Лукойла. Для расчетов коэффициентов воспользуемся надстройкой «Анализ Данных» и разделом «Регрессия». В поле «входной интервал Y» введем значения котировок из столбца “C”. В поле «входной интервал X» введем значения тех же котировок сдвинутых на один интервал. Следует заметить, что последнее значение у сдвинутого интервала “C23” и первое значение “C2” не входит в выделение.

После этого выйдет отчет по регрессии. Разберем более подробно этот отчет. Коэффициент R— квадрат показывает качество модели, чем выше это значение, тем лучше. Р—Значение меньше 15%, значит коэффициенты AR(1), считаются значимыми. Значимость F равна 0 –это говорит о хорошем качестве всего уравнения. Коэффициенты это коэффициенты альфа (α) и бета (β) подобранные для нашей регрессионной модели тренда.

Модель динамики ценной бумаги описывается следующим уравнением:
Y=332.45+0.79*Yt-1
Теперь построим непосредственно сам прогноз по этой модели. Для этого в колонке “E” введем формулу нашей авторегрессии AR(1).
=332.45+0.79*D3
Авторегрессия будет строится только до 23 строчки, пока есть значения курса Лукойла. Далее необходимо прогнозировать уже от предыдущего прогноза, поэтому в ячейке “D24” введем формулу, берущую значения предыдущего прогноза:
“D24” =E23
“D25” =E24 и т.д.
После полученных значений считаем значение нашей прогнозной модели для ячеек “E24 – E27”.

Построим значения исходного ряда и прогнозные значения на основе авторегрессии. Получится следующий график прогнозных значений (зеленый график).

Вывод
Использование регрессионных моделей позволяет построить довольно четкие прогнозные модели. В данной модели использовалась только линейная регрессия, для описания линейных трендов. Так же можно описывать движения ценных бумаг: экспоненциальными, логарифмическими или полиноминальными трендами. На рынках где присутствует сильная нелинейность и хаотичность, использование таких методов не принесет желаемого. Для прогнозирования нелинейных зависимостей используют различные нейронные сети.
© BE in trend
Автор: Жданов Иван
Все курсы > Оптимизация > Занятие 4 (часть 1)
Прежде чем обратиться к теме множественной линейной регрессии, давайте вспомним, что было сделано до сих пор. Возможно, будет полезно посмотреть эти уроки, чтобы освежить знания.
- В рамках вводного курса мы узнали про моделирование взаимосвязи переменных и минимизацию ошибки при обучении алгоритма, а также научились строить несложные модели линейной регрессии с помощью библиотеки sklearn.
- При изучении объектно-ориентированного программирования мы создали класс простой линейной регрессии. Сегодня эти знания пригодятся при создании классов более сложных моделей.
- Также рекомендую вспомнить умножение векторов и матриц.
- Кроме того, в рамках текущего курса по оптимизации мы познакомились с понятием производной и методом градиентного спуска, а также построили модель простой линейной регрессии (использовав метод наименьших квадратов и градиент).
- Наконец, на прошлом занятии мы вновь поговорили про взаимосвязь переменных.
В рамках сегодняшнего занятия мы с нуля построим несколько алгоритмов множественной линейной регрессии.
Регрессионный анализ
Прежде чем обратиться к практике, обсудим некоторые теоретические вопросы регрессионного анализа.
Генеральная совокупность и выборка
Как мы уже знаем, множество всех имеющихся наблюдений принято считать генеральной совокупностью (population). И эти наблюдения, если в них есть взаимосвязи, можно теоретически аппроксимировать, например, линией регрессии. При этом важно понимать, что это некоторая идеальная модель, которую мы никогда не сможем построить.
Единственное, что мы можем сделать, взять выборку (sample) и на ней построить нашу модель, предполагая, что если выборка достаточно велика, она сможет достоверно описать генсовокупность.
Отклонение прогнозного значения от фактического для «идеальной» линии принято называть ошибкой (error или true error).
$$ varepsilon = y-hat{y} $$
Отклонение прогноза от факта для выборочной модели (которую мы и строим) называют остатками (residuals или residual error).
$$ varepsilon = y-f(x) $$
В этом смысле среднеквадратическую ошибку (mean squared error, MSE) корректнее называть средними квадратичными остатками (mean squared residuals).
На практике ошибку и остатки нередко используют как взаимозаменяемые термины.
Уравнение множественной линейной регрессии
Посмотрим на уравнение множественной линейной регрессии.
$$ y = theta_0 + theta_1x_1 + theta_2x_2 + … + theta_jx_j + varepsilon $$
В отличие от простой линейной регрессии в данном случае у нас несколько признаков x (независимых переменных) и несколько коэффициентов $ theta $ («тета»).
Интерпретация результатов модели
Коэффициент $ theta_0 $ задает некоторый базовый уровень (baseline) при условии, что остальные коэффициенты равны нулю и зачастую не имеет смысла с точки зрения интерпретации модели (нужен лишь для того, что поднять линию на нужный уровень).
Параметры $ theta_1, theta_2, …, theta_n $ показывают изменение зависимой переменной при условии «неподвижности» остальных коэффициентов. Например, каждая дополнительная комната может увеличивать цену дома в 1.3 раза.
Переменная $ varepsilon $ (ошибка) представляет собой отклонение фактических данных от прогнозных. В этой переменной могут быть заложены две составляющие. Во-первых, она может включать вариативность целевой переменной, описанную другими (не включенными в нашу модель) признаками. Во-вторых, «улавливать» случайный шум, случайные колебания.
Категориальные признаки
Модель линейной регрессии может включать категориальные признаки. Продолжая пример с квартирой, предположим, что мы строим модель, в которой цена зависит от того, находится ли квартира в центре города или в спальном районе.
Перед этим переменную необходимо закодировать, создав, например, через Label Encoder признак «центр», который примет значение 1, если квартира в центре, и 0, если она находится в спальном районе.
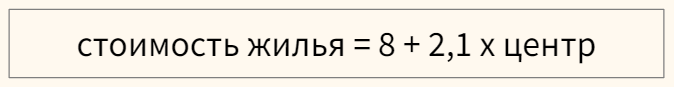
В модели, представленной выше, если квартира находится в центре (переменная «центр» равна единице), ее стоимость составит 10,1 миллиона рублей, если на окраине (переменная «центр» равна нулю) — лишь восемь.
Для категориального признака с множеством классов можно использовать one-hot encoding, если между классами признака отсутствует иерархия,
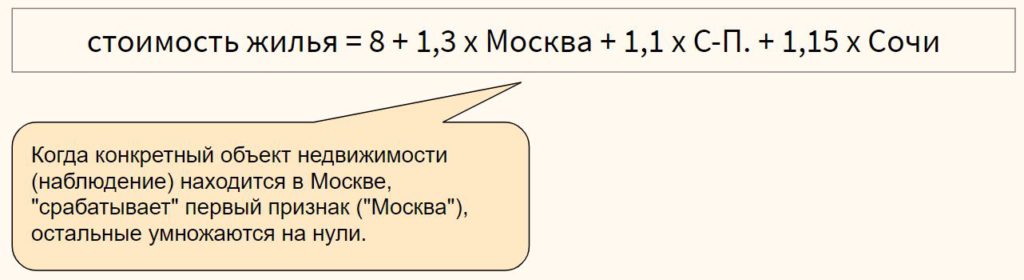
или, например, ordinal encoding в случае наличия иерархии классов в признаке

Выбросы в линейной регрессии
Как и коэффициент корреляции Пирсона, модель линейной регрессии чувствительна к выбросам (outliers), то есть наблюдениям, серьезно выпадающим из общей совокупности. Сравните рисунки ниже.
При наличии выброса (слева), линия регрессии имеет наклон и может использоваться для построения прогноза. Удалив это наблюдение (справа), линия регрессии становится горизонтальной и построение прогноза теряет смысл.
При этом различают два типа выбросов:
- горизонтальные выбросы или влиятельные точки (leverage points) — они сильно отклоняются от среднего по оси x; и
- вертикальные выбросы или просто выбросы (influential points) — отклоняются от среднего по оси y
Ключевое отличие заключается в том, что вертикальные выбросы влияют на наклон модели (изменяют ее коэффициенты), а горизонтальные — нет.
Сравним два графика.
На левом графике черная точка (leverage point) сильно отличается от остальных наблюдений, но наклон прямой линии регрессии с ее появлением не изменился. На правом графике, напротив, появление выброса (influential point) существенно изменяет наклон прямой.
На практике нас конечно больше интересуют influential points, потому что именно они существенно влияют на качество модели.
Если в простой линейной регрессии мы можем оценить leverage и influence наблюдения графически⧉, в многомерной модели это сделать сложнее. Можно использовать график остатков (об этом ниже) или применить один из уже известных нам методов выявления выбросов.
Про выявление leverage и infuential points можно почитать здесь⧉.
Допущения модели регрессии
Применение алгоритма линейной регрессии предполагает несколько допущений (assumptions) или условий, при выполнении которых мы можем говорить о качественно построенной модели.
1. Правильный выбор модели
Вначале важно убедиться, что данные можно аппроксимировать с помощью линейной модели (correct model specification).
Оценить распределение данных можно через график остатков (residuals plot), где по оси x отложен прогноз модели, а на оси y — сами остатки.
В отличие от простой линейной регрессии мы не используем точечную диаграмму X vs. y, потому что хотим оценить зависимость целевой переменной от всех признаков сразу.
Остатки модели относительно ее прогнозных значений должны быть распределены случайным образом без систематической составляющей (residuals do not follow a pattern).
- Если вы попробовали применить линейную модель с коэффициентами первой степени ($x_n^1$) и выявили некоторый паттерн в данных, можно попробовать полиномиальную или какую-либо еще функцию (об этом ниже).
- Кроме того, количественные признаки можно попробовать преобразовать таким образом, чтобы их можно было аппроксимировать прямой линией.
- Если ни то, ни другое не помогло, вероятно данные не стоит моделировать линейной регрессией.
Также замечу, что график остатков показывает выбросы в данных.
2. Нормальность распределения остатков
Среднее значение остатков должно быть равно нулю. Если это не так, и среднее значение меньше нуля (скажем –5), то это значит, что модель регулярно недооценивает (underestimates) фактические значения. В противном случае, если среднее больше нуля, переоценивает (overestimated).
Кроме того, предполагается, что остатки следуют нормальному распределению.
$$ varepsilon sim N(0, sigma) $$
Проверить нормальность остатков можно визуально с помощью гистограммы или рассмотренных ранее критериев нормальности распределения.
Если остатки не распределены нормально, мы не сможем провести статистические тесты на значимость коэффициентов или построить доверительные интервалы. Иначе говоря, мы не сможем сделать статистически значимый вывод о надежности нашей модели.
Причинами могут быть (1) выбросы в данных или (2) неверный выбор модели. Решением может быть, соответственно, исследование выбросов, выбор новой модели и преобразование как признаков, так и целевой переменной.
3. Гомоскедастичность остатков
Гомоскедастичность (homoscedasticity) или одинаковая изменчивость остатков предполагают, что дисперсия остатков не изменяется для различных наблюдений. Противоположное и нежелательное явление называется гетероскедастичностью (heteroscedasticity) или разной изменчивостью.
Гетероскедастичность остатков показывает, что модель ошибается сильнее при более высоких или более низких значениях признаков. Как следствие, если для разных прогнозов у нас разная погрешность, модель нельзя назвать надежной (robust).
Как правило, гетероскедастичность бывает изначально заложена в данные. Ее можно попробовать исправить через преобразование целевой переменной (например, логарифмирование)
4. Отсутствие мультиколлинеарности
Еще одним важным допущением является отсутствие мультиколлинеарности. Мультиколлинеарность (multicollinearity) — это корреляция между зависимыми переменными. Например, если мы предсказываем стоимость жилья по квадратным метрам и количеству комнат, то метры и комнаты логичным образом также будут коррелировать между собой.
Почему плохо, если такая корреляция существует? Базовое предположение линейной регрессии — каждый коэффициент $theta$ оказывает влияние на конечный результат при условии, что остальные коэффициенты постоянны. При мультиколлинеарности на целевую переменную оказывают эффект сразу несколько признаков, и мы не можем с точностью интерпретировать каждый из них.
Также говорят о том, что нужно стремиться к экономной (parsimonious) модели то есть такой модели, которая при наименьшем количестве признаков в наибольшей степени объясняет поведение целевой переменной.
Variance inflation factor
Расчет коэффициента
Variance inflation factor (VIF) или коэффициент увеличения дисперсии позволяет выявить корреляцию между признаками модели.
Принцип расчета VIF заключается в том, чтобы поочередно делать каждый из признаков целевой переменной и строить модель линейной регрессии на основе оставшихся независимых переменных. Например, если у нас есть три признака $x_1, x_2, x_3$, мы поочередно построим три модели линейной регрессии: $x_1 sim x_2 + x_3, x_2 sim x_1 + x_3$ и $x_3 sim x_1 + x_3$.
Обратите внимание на новый для нас формат записи целевой и зависимых переменных модели через символ $sim$.
Затем для каждой модели (то есть для каждого признака $x_1, x_2, x_3$) мы рассчитаем коэффициент детерминации $R^2$. Если он велик, значит данный признак можно объяснить с помощью других независимых переменных и имеется мультиколлинеарность. Если $R^2$ мал, то нельзя и мультиколлинеарность отсутствует.
Теперь рассчитаем VIF на основе $R^2$:
$$ VIF = frac{1}{1-R^2} $$
При таком способе расчета большой (близкий к единице) $R^2$ уменьшит знаменатель и существенно увеличит VIF, при небольшом коэффициенте детерминации коэффициент увеличения дисперсии наоборот уменьшится.
Замечу, что $1-R^2$ принято называть tolerance.
Другие способы выявления мультиколлинеарности
Для выявления корреляции между независимыми переменными можно использовать точечные диаграммы или корреляционные матрицы. При этом важно понимать, что в данном случае мы выявляем зависимость лишь между двумя признаками. Корреляцию множества признаков выявляет только коэффициент увеличения дисперсии.
Интерпретация VIF
VIF находится в диапазон от единицы до плюс бесконечности. Как правило, при интерпретации показателей variance inflation factor придерживаются следующих принципов:
- VIF = 1, между признаками отсутствует корреляция
- 1 < VIF $leq$ 5 — умеренная корреляция
- 5 < VIF $leq$ 10 — высокая корреляция
- Более 10 — очень высокая
После расчета VIF можно по одному удалять признаки с наибольшей корреляцией и смотреть как изменится этот показатель для оставшихся независимых переменных.
5. Отсутствие автокорреляции остатков
На занятии по временным рядам (time series), мы сказали, что автокорреляция (autocorrelation) — это корреляция между значениями одной и той же переменной в разные моменты времени.
Применительно к модели линейной регрессии автокорреляция целевой переменной (для простой линейной регрессии) и автокорреляция остатков, residuals autocorrelation (для модели множественной регрессии) означает, что результат или прогноз зависят не от признаков, а от самой этой целевой переменной. В такой ситуации признаки теряют свою значимость и применение модели регрессии становится нецелесообразным.
Причины автокорреляции остатков
Существует несколько возможных причин:
- Прогнозирование целевой переменной с высокой автокорреляцией (например, если мы моделируем цену акций с помощью других переменных, то можем ожидать высокую автокорреляцию остатков, поскольку цена акций как правило сильно зависит от времени)
- Удаление значимых признаков
- Другие причины
Автокорреляция первого порядка
Дадим формальное определение автокорреляции первого порядка (first order correlation), то есть автокорреляции с лагом 1.
$$ varepsilon_t = pvarepsilon_{t-1} + u_t $$
где $u_t$ — некоррелированная при различных t одинаково распределенная случайная величина (independent and identically distributed (i.i.d.) random variable), а $p$ — коэффициент автокорреляции, который находится в диапазоне $-1 < p < 1$. Чем он ближе к нулю, тем меньше зависимость остатка $varepsilon_t$ от остатка предыдущего периода $varepsilon_{t-1}$.
Такое уравнение также называется схемой Маркова первого порядка (Markov first-order scheme).
Обратите внимание, что для модели автокорреляции первого порядка коэффициент автокорреляции $p$ совпадает с коэффициентом авторегрессии AR(1) $varphi$.
$$ y_t = c + varphi cdot y_{t-1} $$
Разумеется, мы можем построить модель автокорреляции, например, третьего порядка.
$$ varepsilon_t = p_1varepsilon_{t-1} + p_2varepsilon_{t-2} + p_3varepsilon_{t-3} + u_t $$
Выявление автокорреляции остатков
Для выявления автокорреляции остатков можно использовать график последовательности и график остатков с лагом 1, график автокорреляционной функции или критерий Дарбина-Уотсона.
График последовательности и график остатков с лагом 1
На графике последовательности (sequence plot) по оси x откладывается время (или порядковый номер наблюдения), а по оси y — остатки модели. Кроме того, на графике остатков с лагом 1 (lag-1 plot) остатки (ось y) можно сравнить с этими же значениями, взятыми с лагом 1 (ось x).
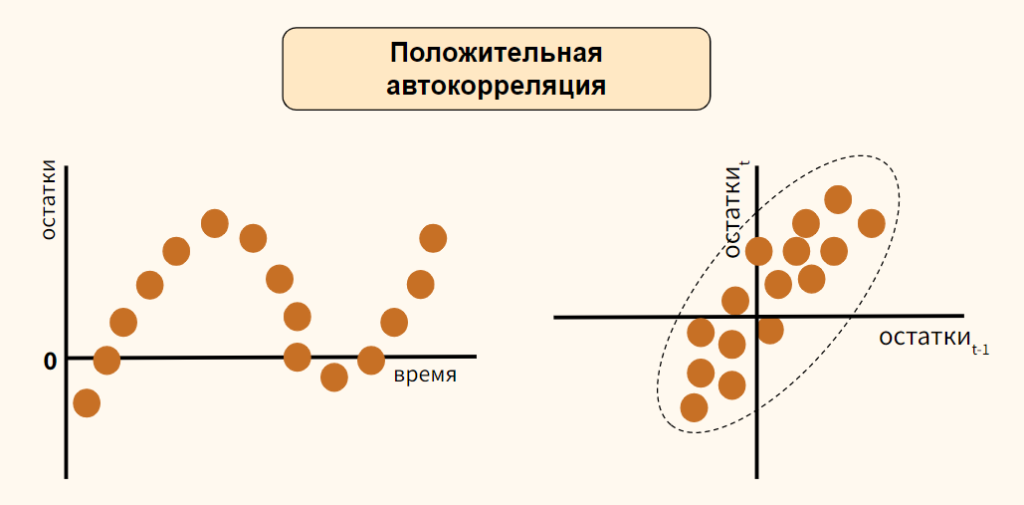
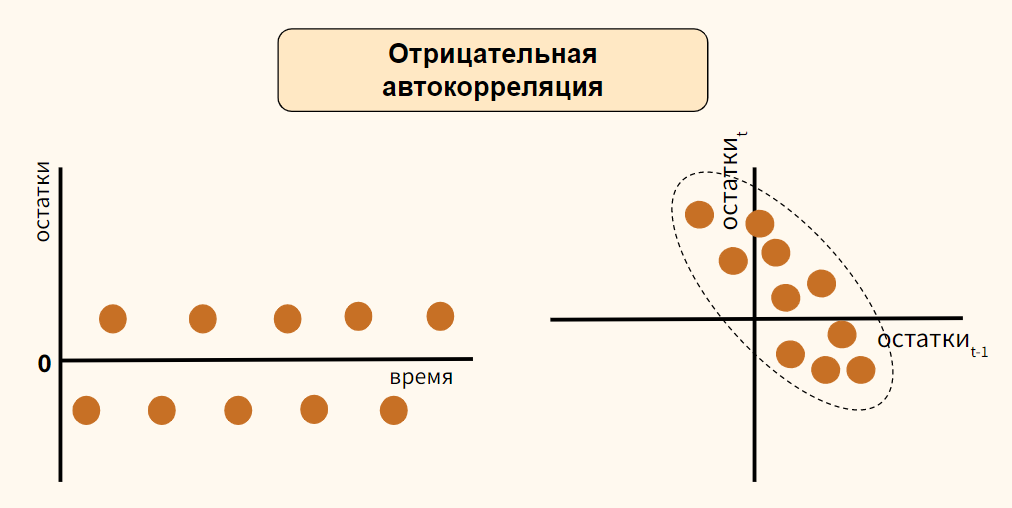
Рассмотрим вариант положительной автокорреляции (positive autocorrelation) на графиках остатков типа (а) и (б).
Как вы видите, при положительной автокорреляции в большинстве случаев, если одно наблюдение демонстрирует рост по отношению к предыдущему значению, то и последующее будет демонстрировать рост, и наоборот.
Теперь обратимся к отрицательной автокорреляции (negative autocorrelation).
Здесь наоборот, если одно наблюдение демонстрирует рост показателя по отношению к предыдущему значению, то последующее наблюдение будет наоборот снижением. Опять же справедливо и обратное утверждение.
В случае отсутствия автокорреляции мы не должны увидеть на графиках какого-либо паттерна.
График автокорреляционной функции
Еще один способ выявить автокорреляцию — построить график автокорреляционной функции (autocorrelation function, ACF).
Напомню, такой график показывает автокорреляцию данных с этими же данными, взятыми с первым, вторым и последующими лагами.
Критерий Дарбина-Уотсона
Количественным выражением автокорреляции является критерий Дарбина-Уотсона (Durbin-Watson test). Этот критерий выявляет только автокорреляцию первого порядка.
- Нулевая гипотеза утверждает, что такая автокорреляция отсутствует ($p=0$),
- Альтернативная гипотеза соответственно утверждает, что присутствует
- Положительная ($p approx -1$) или
- Отрицательная ($p approx 1$) автокорреляция
Значение теста находится в диапазоне от 0 до 4.
- При показателе близком к двум можно говорить об отсутствии автокорреляции
- Приближение к четырем говорит о положительной автокорреляции
- К нулю, об отрицательной
Как избавиться от автокорреляции
Автокорреляцию можно преодолеть, добавив значимый признак в модель, выбрав иной тип модели (например, полиномиальную регрессию) или в целом перейдя к моделированию и прогнозированию временного ряда.
Рассмотрение этих методов находится за рамками сегодняшнего занятия. Перейдем к практике.
УДК 519.2
ОБ ОДНОМ МЕТОДЕ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ АВТОРЕГРЕССИОННЫХ МОДЕЛЕЙ ВРЕМЕННОГО РЯДА
ИЛ. Ильин (Ком! У), П.П. Ильина (КанчатПУ)
Предлагаете» метод построения авторегрессионных моделей временных рядов, основанный по новаи способе вычисления коэффициентов модеяей.
The ит) rk offer* the method of building of auto-regression temporary series modcJs, based on the new и •ay of calculation of model coefficients.
Временные ряды имеют широкое применение в различных задачах, связанных с обработкой информации. При построении авторегрессионных моделей временных рядов для определения коэффициентов обычно используются уравнения Юла Уокера В данной работе предлагается метод определения коэффициентов регрессионных моделей, который и ряде случаев по1воляе1 троить более адекватные молсли без увеличении их порядка.
Моделью авторегрессии к го порядка временного ряда
г(1), д.(2), …,.фг)
называется модель вила
x{t)-<xhx{l 1) + а.)Х(1 -2) + … + «*-<</ — Аг) + s,, (1)
где к порядок модели;
а, коэффициенты модели; с, случайная ошибка.
При пом нредполагаегся, что к,у t = 1,2,…— независимые случайные величины с нулевым математическим ожиданием и одинаковой дисперсией о
Ьудсм также полагать, »по исходный временной ряд является стационарным к широком смысле и Щх( 01-0.
Ич pa6oi [I 3| известно, что сисгема уравнений Юла Уокера л_чи определения коэффициен-юв модели имеет следующий вид:
/?(!) = cxi + а2/?(1)4- …» <х^/?(А — 1),
/?(2) = а,У?(1) +а2 …+ щЛ(А 2),
ад = а,«(А-1) +а:Л(А-2)+ …+СЇІ, (2)
-1-£(x(i)-x)(x(i + x)-x) где /?(т) =—Т ‘-L~г—————ПРИ t “ I» 2,…. к
TfZwO-ï)* п 1-І
являются точечными выборочными оценками значений функции автокорреляции.
Замелім, что решение системы (2) зависит только от первых к значений автокорреляционной функции и не зависит от всех последующих. Потому автокорреляционная модель Юла Уокера не учитывает святей между значениями временного ряда, которые сдвинуты более чем на к значений. В тех случаях, когда автокорреляционна« функция временного ряда мала при ма-гшх И, но достигает максимума при к = £,,, модели авторегрессии порядка к < А„ не могут быть достаточно точными, если их коэффициенты вычисляются на основании системы Юла Уокера
Заметим, что осли временной ряд точно представляется авторегрессионной моделью А-го юрядка. то для значений функции автокорреляции г(/) при всех / выполняется равенсіво
г(/) = 0|Г(/- 1) +аг^?-2) … +сііГ(і-к) при/= 1,2, … (3)
Заменяя ы уравнении (3) величины r(i) точечными выборочными оценками значений функции автокорреляции /?(/), получим новую систему уравнений для определения коэффициентов
вестник Камчатского пхударсп№1тоготехничспиио университета
а,. В этой системе первые к уравнений совпадают с уравнениями Юла Уокера, а последующие имеют вид, соответствующий уравнению (3):
/?(1) = а( + а?Л(1)-^… +а*Л(А- 1),
Л(2) = а, Л( I) + а> + ,..+ а»/?(А — 2),
/?(А:) = U|Ä(4- 1) + a2R(k 2) + … + сц, (4)
R(k + 1) = іі.ВД + агЯ(к — I) • … — а^(1).
Л(А/) = а ,/?(Л/- 1) + а; ЩХ1-2) +… + щ/ЦМ-к).
Величина Л/вьібираеіся такой. чтобы в систему (4) вошли всс значимо отличные or ну.ія коэффициенты Л(7).
Запишем ?ту систему ы матричной форме:
Ла = 91. (5)
11од решением этой системы будем понимать обобщенное решение, вычисляемое по формуле
а = (ЛТЛ)»‘ ЛТ’Л. (6)
«ia мстим, что если матрица Л является квадратной и имеет оброчную матрицу, то обобщенное решение (6) совпадет с классическим решением системы Юла Уокера. Однако обобщенное
решение (6) в опосредствованном виде учитывает все значимо отличные от нуля значения авто-
корреляционной функции ф). Можно предположить, что модифицированная авторегрессионная модель типа (1), коэффициенты которой находя іем из системы (4). будет более адекватной, чем классическая модель авторегрессии.
Проведенные численные эксперименты показывают, »сто в подавляющем большинстве случаев что предположение оказывается верным. Исключения появляются лишь тогда, когда элементы временного ряда с большой степенью точности изначально определяются соотношением (1), т. с. значения автокорреляционной функции r(i) при і > к незначимо отличны от нуля.
Литература
1. Box Ci Е. P.. Jenkins О.М. Time scries analysis. — San-Francisco: IIolden Day. 1970. — P. 216.
2. Box G.E. P., Jenkins ü.M. Time series analysis: Forecasting and соп і тої. San-Francisoo: Holden Day, 1976. — P. 22«.
3. Тихомиров H.H., Дорогими F../О. Эконометрика. М.: Экзамен, 2003 — С. 510.
Модель авторегрессии
Предположим, у нас имеется временной ряд Z(t), представленный на рисунке ниже. Нужно вычислить будущее значение временного ряда в точке №41, то есть значение Z(41) (красный цвет) на основании 40 предыдущих точек Z(1), Z(2),…,Z(40) с использованием модели авторегрессии.
Формула для определения Z(41) выглядит следующим образом и называется авторегрессией порядка p:
В это формуле мы знаем значения Z(40), Z(39), Z(38) и т.д., но не знаем коэффициенты a. Как их определить?
Если для Z(41) работает такая зависимость, значит, она работает и для предыдущих точек, т.е. мы можем получить систему уравнений:
В этой системе уравнений мы знаем все значения Z(t), а, следовательно, можем легко определить коэффициенты a. Самый легкий способ определения коэффициентов — использование метода наименьших квадратов.
Два важных вопроса, которые нужно решить при использовании модели авторегрессии:
- Каков должен быть порядок p?
- Сколько уравнений нужно добавлять в матрицу, чтобы найденные коэффициенты авторегрессии a давали максимально точный прогноз?
Однозначных ответов на эти вопросы нет. Исследование функции автокорреляции для определения p на сегодняшний день отошло в прошлое, так как длина временных рядов имеет сотни и тысячи значений. Количество принимаемых в расчет уравнений часто зависит от сезонности временного ряда. Ответы на эти вопросы и должен найти разработчик данной модели, чтобы заставить ее прогнозировать надежно!
Модель авторегрессии с одной стороны довольно проста, так как принцип ее работы понятен и нагляден; с другой — сложна тем, что в ней имеет место множество нюансов, которые требуют кропотливого труда разработчика. Однако, не смотря на все нюансы, рассмотренная модель является частью большой модели ARIMAX, которая на сегодняшний день чрезвычайно популярна для решения задач прогнозирования временных рядов.