Как найти коэффициент увеличения линзы - AvtoShod.ru

Загрузить PDF

Оптическое увеличение – это отношение линейных или угловых размеров изображения и предмета.^[1] Например, линза, увеличивающая размеры предмета, имеет большое увеличение, а линза, уменьшающая размеры предмета, имеет малое увеличение. Увеличение, как правило, вычисляется по формуле M = (h_i/h_o) = -(d_i/d_o), где М – увеличение, h_i – высота изображения, h_o – высота объекта, d_i и d_o – расстояние до изображения и предмета.

Примечание: собирающая линза широкая посередине и узкая по краям; рассеивающая линза широкая по краям и узкая посередине.^[2] Процесс вычисления увеличения одинаков для обеих линз за одним исключением в случае рассеивающей линзы.

1
Напишите формулу. Теперь определите, какие переменные вам даны. По формуле вы можете найти любую переменную, входящую в формулу (а не только увеличение).
- Например, рассмотрим фигурку высотой 6 см, которая находится на расстоянии 50 см от собирающей линзы с фокусным расстоянием 20 см. Здесь вы должны найти увеличение, размер изображения и расстояние до изображения. Запишите формулу так:
  
  M = (h_i/h_o) = -(d_i/d_o)
- В задаче даны h_o (высота фигурки) и d_o (расстояние от фигурки до линзы). Вы также знаете фокусное расстояние линзы, которое не входит в формулу. Вы должны найти h_i, d_i и M.
2
Используйте формулу линзы для вычисления d_i, если вы знаете расстояние от линзы до предмета и фокусное расстояние линзы. Формула линзы: 1/f = 1/d_o + 1/d_i, где f = фокусное расстояние линзы.
- В нашем примере:
  
  1/f = 1/d_o + 1/d_i
  
  1/20 = 1/50 + 1/d_i
  
  5/100 — 2/100 = 1/d_i
  
  3/100 = 1/d_i
  
  100/3 = d_i = 33,3 см
- Фокусное расстояние линзы – это расстояние от центра объектива до точки, в которой сходятся лучи света. В задачах фокусное расстояние, как правило, дано. В реальной жизни фокусное расстояние наносится на оправу линзы.^[3]
3
Теперь вы знаете d_o и d_i и можете найти высоту увеличенного изображения и увеличение линзы. Обратите внимание, что формула для вычисления увеличения включает два знака равенства (M = (h_i/h_o) = -(d_i/d_o)), то есть оба отношения равны, и вы можете воспользоваться этим фактом при вычислении M и h_i.
- В нашем примере найдите h_i следующим образом:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(33,3/50)
  
  h_i = -(33,3/50) × 6
  
  h_i = -3,996 см
- Обратите внимание, что отрицательная высота означает, что изображение будет перевернутым.
4
Для вычисления М используйте либо –(d_i/d_o), либо (h_i/h_o).
- В нашем примере:
  
  M = (h_i/h_o)
  
  M = (-3,996/6) = -0,666
- Вы получите тот же результат, используя значения d:
  
  M = -(d_i/d_o)
  
  M = -(33,3/50) = -0,666
- Обратите внимание, что увеличение не имеет единиц измерения.
5
Если у вас есть значение увеличения, вы можете предположить некоторые свойства изображения.
- Размер изображения. Чем больше значение М, тем больше изображение. Значения M между 1 и 0 свидетельствуют о том, что предмет через линзу будет выглядеть меньше.
- Ориентация изображения. Отрицательные значения М указывают на то, что изображение предмета будет перевернутым.
- В нашем примере М = -0,666, то есть изображение фигурки будет перевернутым и составлять две трети высоты фигурки.
6
В случае рассеивающей линзы используйте отрицательное значение фокусного расстояния. Это единственное отличие вычисления увеличения рассеивающей линзы от вычисления увеличения собирающей линзы (все формулы остаются теми же). В нашем примере этот факт повлияет на значение d_i.
- Проделаем вычисления для нашего примера еще раз, но при условии, что мы используем рассеивающую линзу с фокусным расстоянием -20 см. Все другие значениями остаются такими же.
- Во-первых, найдем d_i через формулу линзы:
  
  1/f = 1/d_o + 1/d_i
  
  1/-20 = 1/50 + 1/d_i
  
  -5/100 — 2/100 = 1/d_i
  
  -7/100 = 1/d_i
  
  -100/7 = d_i = -14,29 см
- Теперь найдем h_i и M.
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(-14,29/50)
  
  h_i = -(-14,29/50) × 6
  
  h_i = 1,71 см
  
  M = (h_i/h_o)
  
  M = (1,71/6) = 0,285
Реклама

Две линзы

1
Найдите фокусное расстояние обеих линз. Когда вы имеете дело с системой, состоящей из двух линз, которые расположены параллельно друг другу (например, как в телескопе), вам нужно определить фокусное расстояние обеих линз, чтобы найти увеличение такой системы. Это можно сделать по формуле M = f_o/f_e.^[4]
- В формуле f_o – это фокусное расстояние линзы объектива, f_o – это фокусное расстояние линзы окуляра (к окуляру вы прикладываете глаз).
2
Подставьте значения фокусных расстояний в формулу, и вы найдете увеличение системы из двух линз.
- Например, рассмотрим телескоп, в котором фокусное расстояние линзы объектива равно 10 см, а фокусное расстояние линзы окуляра равно 5 см. М = 10/5 = 2.
Реклама

Детальный метод

1
Найдите расстояние между линзами и предметом. Если перед предметом расположены две линзы, можно вычислить увеличение конечного изображения, зная расстояния от предмета до линз, высоту предмета и фокусные расстояния обеих линз.
- Рассмотрим предыдущий пример – фигурку высотой 6 см, которая находится на расстоянии 50 см от собирающей линзы с фокусным расстоянием 20 см и на расстоянии 100 см от второй линзы с фокусным расстоянием 5 см. Найдите увеличение такой системы линз.
2
Найдите расстояние до изображения, его высоту и увеличение первой линзы. Начните с ближайшей к фигурке линзы и по формуле линзы найдите расстояние до изображения, а затем по формуле для вычисления увеличения найдите высоту изображения и увеличение.
- В предыдущем разделе мы выяснили, что первая линза дает изображение высотой -3,996 см, расстояние до изображения равно 33,3 см, а увеличение равно -0,666.
3
Используйте изображение от первой линзы в качестве предмета для второй линзы. Теперь вы можете найти увеличение второй линзы, высоту изображения и расстояние до него; для этого используйте те же методы, которые вы использовали для первой линзы, только в этот раз вместо фигурки воспользуйтесь изображением от первой линзы.
- В нашем примере изображение находится на расстоянии 33,3 см от первой линзы, поэтому находится на расстоянии 50-33,3 = 16,7 см от второй линзы. Найдем расстояние до изображения от второй линзы, используя найденное расстояние до предмета и фокусное расстояние второй линзы.
  
  1/f = 1/d_o + 1/d_i
  
  1/5 = 1/16,7 + 1/d_i
  
  0,2 — 0,0599 = 1/d_i
  
  0,14 = 1/d_i
  
  d_i = 7,14 см
- Теперь мы можем найти h_i и M для второй линзы:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/-3,996) = -(7,14/16,7)
  
  h_i = -(0,427) × -3,996
  
  h_i = 1,71 см
  
  M = (h_i/h_o)
  
  M = (1,71/-3,996) = -0,428
4
Продолжайте описанный процесс вычислений для любого числа дополнительных линз. Для каждой последующей линзы предметом считайте изображение от предыдущей линзы и используйте формулу линзы и формулу для вычисления увеличения.
- Имейте в виду, что последующие линзы могут переворачивать изображение. Например, полученное выше значение увеличения (-0,428) свидетельствует о том, что изображение от второй линзы будет составлять 4/10 размера изображения предмета от первой линзы, но теперь изображение фигурки не будет перевернутым (вторая линза перевернет «перевернутое» изображение от первой линзы).
Реклама

Советы

На биноклях, как правило, стоит такая маркировка: число х число, например, 8×25 или 8×40. В этом случае первое число – это увеличение бинокля. Второе число относится к четкости изображения.
Заметьте, что для системы, состоящей из одной линзы, увеличение будет отрицательным в случае, если расстояние до предмета превышает фокусное расстояние линзы. Это не означает, что изображение предмета будет меньше его действительной высоты. Просто в данном случае изображение будет перевернутым.

Об этой статье

Эту страницу просматривали 31 962 раза.

Была ли эта статья полезной?

Источник

Условие задачи:

Предмет находится на расстоянии (4F) от собирающей линзы. Найдите коэффициент увеличения линзы.

Задача №10.5.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(d=4F), (Gamma-?)

Решение задачи:

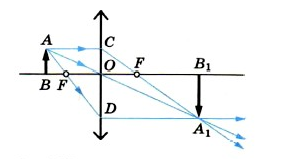
Понятно, что в задаче просят найти поперечное увеличение линзы (Gamma) (странно, что его назвали коэффициентом увеличения).

Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A₁. Проекция этой точки на главную оптическую ось есть точка B₁. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и уменьшенным (так как (d > 2F))

Запишем формулу тонкой линзы:

[frac{1}{F} = frac{1}{d} + frac{1}{f};;;;(1)]

В этой формуле (F) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, (d) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), (f) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).

Поперечное увеличение линзы (Gamma) определяют по следующей формуле (она выводится из подобия треугольников AOB и A₁OB₁ по трем углам):

[Gamma = frac{f}{d};;;;(2)]

Из уравнения (1) будем выражать расстояние от линзы до изображения (f), для чего в правой части уравнения (1) приведем под общий знаменатель:

[frac{1}{F} = frac{{f + d}}{{df}}]

Перемножим “крест-накрест”:

[df = Ff + Fd]

[df – Ff = Fd]

[fleft( {d – F} right) = Fd]

[f = frac{{dF}}{{d – F}}]

Полученное выражение подставим в формулу (2):

[Gamma = frac{{dF}}{{dleft( {d – F} right)}}]

[Gamma = frac{F}{{d – F}}]

По условию задачи предмет находится на расстоянии (4F) от собирающей линзы, то есть (d=4F), поэтому:

[Gamma = frac{F}{{4F – F}} = frac{1}{3}]

Ответ: 1/3.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.5.13 Оптическая сила тонкой линзы 5 дптр. Предмет поместили на расстоянии 60 см
10.5.15 На каком расстоянии от линзы с оптической силой 5 дптр необходимо поставить предмет
10.5.16 Фокусное расстояние собирающей линзы 0,2 м. На каком расстоянии от линзы следует

Источник

Линзы, как биологические, так и синтетические, представляют собой чудеса оптической физики, которые используют способность определенных сред преломлять или изгибать световые лучи. Они бывают двух основных форм: выпуклые или изогнутые наружу и вогнутые или изогнутые внутрь. Одна из их основных целей — увеличить изображения или сделать их больше, чем они есть на самом деле.

Линзы можно найти в телескопах, микроскопах, биноклях и других оптических приборах, а также в вашем собственном глазу. Ученые и студенты имеют в своем распоряжении ряд простых алгебраических уравнений, чтобы связать физические размеры и форму линзы с ее воздействием на световые лучи, которые проходят через нее.

Линзы и физика увеличения

Большинство «искусственных» линз сделаны из стекла. Причина, по которой линзы преломляют свет, состоит в том, что когда световые лучи перемещаются из одной среды (например, воздуха, воды или другого физического материала) в другую, их скорость изменяется очень незначительно, и в результате лучи меняют курс.

Когда световые лучи попадают в двойную выпуклую линзу (то есть ту, которая выглядит как сплющенный овал со стороны) в направлении, перпендикулярном поверхности линзы, лучи, ближайшие к каждому краю, резко преломляются к центру, сначала при входе в линзу и снова при уходе. Те, кто ближе к середине, изогнуты меньше, а те, которые проходят перпендикулярно через центр, вообще не преломляются. В результате все эти лучи сходятся в фокусной точке ( F ) на расстоянии f от центра линзы.

Уравнение тонкой линзы и коэффициент увеличения

Изображения, полученные с помощью линз и зеркал, могут быть реальными (то есть проецируемыми на экран) или виртуальными (то есть не проецируемыми). По соглашению, значения расстояний реальных изображений ( i ) от линзы являются положительными, а значения виртуальных изображений — отрицательными. Расстояние самого объекта от объектива ( o ) всегда положительное.

Выпуклые (сходящиеся) линзы создают реальные изображения и связаны с положительным значением f , тогда как вогнутые (расходящиеся) линзы создают виртуальные изображения и имеют отрицательное значение f .

Фокусное расстояние f , расстояние до объекта o и расстояние до изображения i связаны уравнением тонкой линзы:

Гидроразрыва {1} {O} + гидроразрыва {1} {I} = гидроразрыва {1} {F}

При этом формула увеличения или коэффициент увеличения ( м ) связывают высоту изображения, создаваемого объективом, с высотой объекта:

т = гидроразрыва {-i} {о}

Помните, я негативно отношусь к виртуальным изображениям.

Человеческий глаз

Линзы ваших глаз действуют как сходящиеся линзы.

Как вы могли бы предсказать, исходя из того, что вы уже прочитали, ваши глазные линзы выпуклые с обеих сторон. Если бы ваши линзы были не только выпуклыми, но и гибкими, свет, проходящий через ваши глаза, воспринимался бы вашим мозгом гораздо более хаотично, чем на самом деле, и людям было бы ужасно трудно ориентироваться в мире (и, вероятно, не выжил бы в поисках интернета для науки Информация).

Сначала свет попадает в глаз через роговицу, выпуклый наружный слой передней части глазного яблока. Затем он проходит через зрачок, диаметр которого можно регулировать с помощью крошечных мышц. Линза находится позади зрачка. Часть глаза, на которой формируется изображение, которая находится на внутренней стороне нижней задней части глазного яблока, называется сетчаткой . Визуальная информация передается из сетчатки в мозг через зрительные нервы.

Калькулятор увеличения

Вы можете найти веб-сайты, которые помогут вам решить некоторые из этих проблем, как только вы освоитесь с основами физики, пройдя некоторые из них самостоятельно. Основная идея состоит в том, чтобы понять, как различные компоненты уравнения линзы связаны друг с другом и почему изменения переменных приводят к действительным эффектам, которые они оказывают.

Пример такого онлайн-инструмента приведен в Ресурсах.

Источник

Ещё одним параметром, характеризующий систему из линз и сферических зеркал, является линейное увеличение.

Линейным увеличением называется отношение высоты получившегося изображения к высоте предмета:

Г $displaystyle =frac{{{h}_{iz}}}{{{h}_{pr}}}$ (1)

где

Вопрос о поиске данного параметра может возникнуть и в задачах на построение, и в задачах на формулы тонкой линзы и сферического зеркала.

Пусть даны предмет, линза и изображение предмета в линзе (рис. 1).

Рис. 1. Линейное увеличение

При построении мы использовали луч от предмета ( displaystyle S ), который проходит через главный оптический центр линзы (при этом не преломляясь). При этом у нас получились два подобных треугольника (подобие по трём углам). Тогда, используя подобие, можем записать:

Г $displaystyle =frac{{{h}_{iz}}}{{{h}_{pr}}}=frac{f}{d}$ (2)

где

Вывод: вопросы, связанные с линейным увеличением, решаются или через логику построения в системах (рис.1), или через соотношение (2) при наличии численных значений параметров линз.

Источник

Определение

Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.

Условные обозначения:

расстояние от предмета до линзы — d (м);
расстояние от изображения до линзы— f (м);
фокусное расстояние линзы — F (м).

Вывод формулы

Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:

Видно, что треугольники АОВ и А₁В₁О подобные (по двум углам). Следовательно:

BOOB1=ABA1B1

По двум углам также являются подобными треугольники COF и FA₁B₁. Отсюда делаем вывод, что:

COA1B1=OFFB1

Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:

AB=CO

Следовательно:

ABA1B1=COA1B1

Отсюда следует, что:

BOOB1=OFFB1

BO является расстоянием от предмета до линзы. Обозначим его за d. OB1 является расстоянием от линзы до изображения. Обозначим его за f. OF является фокусным расстоянием линзы. Обозначим его за F. FB1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:

df=Ff−F

Избавимся от знаменателей и получим:

fd−Fd=fF

Или можно записать так:

fF+Fd=fd

Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:

Формула тонкой линзы

1d+1f=1F

Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:

1d+1f=D

Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.

Правила расстановки знаков перед членами уравнения в формуле линзы

Если линза собирающая, то ее фокус действительный, и перед членом 1F ставят знак «плюс» (1F).
Если линза рассеивающая, то ее фокус мнимый, и перед членом 1F ставят знак «минус» (−1F).
Если изображение действительное, то перед величиной 1d ставят знак «плюс» (1d).
Если изображение мнимое, то перед величиной 1d ставят знак «минус» (−1d).
Величина 1f всегда имеет знак «плюс», поскольку расстояние от предмета до линзы всегда положительное.

Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.

Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.

Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.

Применим формулу тонкой линзы:

1d+1f=1F

1d+115=110

Умножим выражение на 150d:

150+10d=15d

5d=150

d=30 (см)

Увеличение линзы

Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.

Определение

Линейное увеличение — отношение линейного размера изображения к линейному размеру предмета. Линейное увеличение обозначают буквой Γ.

Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А₁В₁ равна Н, то:

Γ=Hh

Мы уже выяснили, что треугольники АОВ и ОА₁В₁ подобны. Поэтому:

Hh=|f||d|

Где H — высота изображения предмета, h — высота самого предмета.

Отсюда вытекает, что увеличение линзы равно:

Γ=|f||d|

Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?

2 см = 0,02 м

Сначала применим формулы тонкой линзы:

1d+1f=1F

Она необходима, чтобы выразить фокусное расстояние линзы:

F=dfd+f

Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:

Γ=fd=Hh

Отсюда это расстояние равно:

d=fhH

Подставим полученное выражение в формулу фокусного расстояния линзы:

F=fhHffhH+f=f2hH·
Hfh+fH=fhH+h

F=fhH+h=4·0,021+0,02≈0,08 (м)=8 (см)

Задание EF17760

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Сделать рисунок — построить изображение в линзе.

3.Записать формулу для нахождения площади полученной фигуры.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Оптическая сила линзы: D = 2,5 дптр.

• Сторона треугольника AC = 4 см.

4 см = 0,04 м

Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.

Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.

Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:

1d+1f=1F

Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:

12F+1f=1F

1f=1F−12F=2−12F=12F

f=2F

Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:

S=A´C´·B´C´2

Из формулы оптической силы линзы найдем фокусное расстояние:

F=1D=12,5=0,4 (м)

Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:

dC=2F−AC=2·0,4−0,04=0,76 (м)

Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:

10,76+1f=1F

1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4

fC=0,76·0,40,76−0,4=0,844 (м)

Тогда длина катета A´ C´ будет равна:

A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)

Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:

BCB´C´=ACA´C´

Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:

ACB´C´=ACA´C´

Следовательно:

B´C´=A´C´

Отсюда площадь треугольника равна:

S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17685

Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?

Ответ:

а) 0,50 м

б) 0,75 м

в) 1,25 м

г) 1,50 м

Алгоритм решения

1.Записать известные данные.

2.Записать формулу увеличения линзы и формулу тонкой линзы.

3.Выразить из обеих формул расстояние от линзы до изображения предмета.

4.Приравнять правые части выражений.

5.Выполнить решение в общем виде.

6.Подставить известные данные и вычислить искомую величину.

Решение

Запишем известные данные:

• Фокусное расстояние линзы: F = 1 м.

• Увеличение линзы: Γ = 4.

Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:

Γ=fd

f=Γd

Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:

1d+1f=1F

1f=1F−1d=d−FFd

f=dFd−F

Приравняем правые части последних выражений:

Γd=dFd−F

Поделим на d и выразим расстояние от предмета до линзы:

Γ=Fd−F

d=FΓ+F=14+1=1,25 (м)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18124

Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.

Ответ:

а) 5 см

б) 10 см

в) 20 см

г) 36 см

Алгоритм решения

1.Записать известные данные.

2.Записать формулу увеличения линзы в двух вариантах и выразить из нее расстояние от изображения до линзы.

3.Записать формулу тонкой линзы и тоже выразить из нее расстояние от изображения до линзы.

4.Приравнять правые части выражений.

5.Выполнить решение в общем виде.

6.Подставить известные данные и вычислить искомую величину.

Решение

Запишем известные данные:

• Расстояние от оптического центра линзы до предмета: d = 30 cм.

• Высота предмета: h = 6 см.

• Высота изображения: H = 12 см.

Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.

Запишем формулу увеличения линзы:

Γ=Hh=fd

Отсюда расстояние от изображения до линзы равно:

f=Hdh

Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:

1d+1f=1F

1f=1F−1d=d−FFd

f=dFd−F

Приравняем правые части последних выражений:

Hdh=dFd−F

Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:

Hh=Fd−F

H(d−F)=hF

Hd−HF=hF

hF+HF=Hd

F(h+H)=Hd

F=Hdh+H=12·3012+6=20 (см)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19112

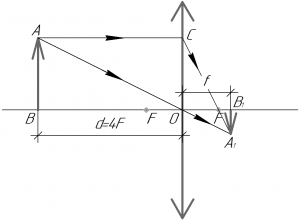
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

3.Записать формулу тонкой линзы и определить из нее расстояние от изображения до линзы.

4.Записать формулу линейного увеличения линзы двумя способами для вычисления радиусов окружностей, по которым движутся точка и ее изображение.

5.Выполнить решение в общем виде.

6.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Фокусное расстояние линзы: F = 10 см.

• Расстояние от линзы до плоскости, в которой вращается точка: d = 15 см.

• Скорость вращения точки: v = 5 м/с.

10 см = 0,1 м

15 см = 0,15 м

Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.

Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.

Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:

1d+1f=1F

1f=1F−1d=d−FFd

f=dFd−F

Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:

Γ=Rr

Линейное увеличение также определяется формулой:

Γ=fd

Следовательно:

Rr=fd

Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:

Rr=dFd(d−F)=Fd−F

Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:

ω=vr=VR

Отсюда линейная скорость движения изображения равна:

V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 14.9k

Источник

Две линзы

Детальный метод

Советы

Об этой статье

Была ли эта статья полезной?

Условие задачи:

Дано:

Решение задачи:

Ответ: 1/3.

Смотрите также задачи:

Линзы и физика увеличения

Уравнение тонкой линзы и коэффициент увеличения

Человеческий глаз

Калькулятор увеличения

Вывод формулы

Увеличение линзы

Не пропустите также: