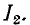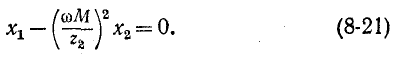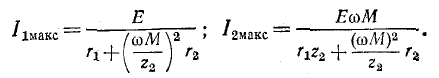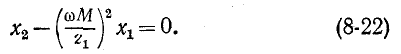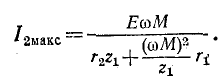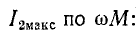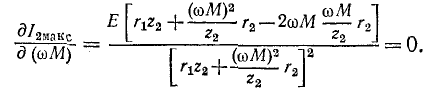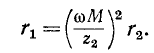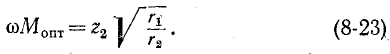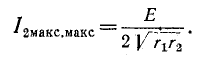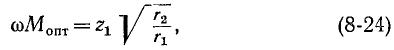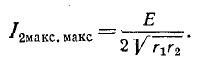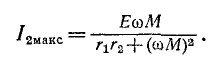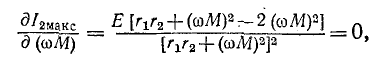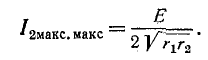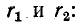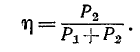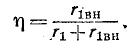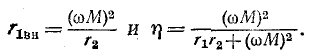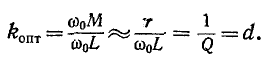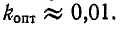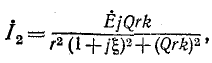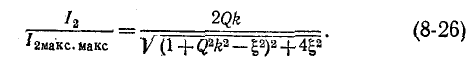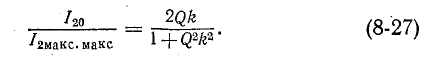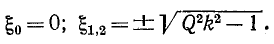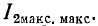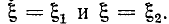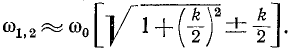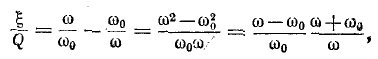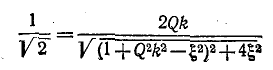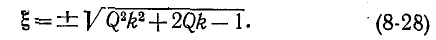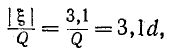Содержание:
Индуктивно связанные электрические цепи:
При изменении магнитного поля, связанного с каким-либо витком, в последнем наводится э. д. с., которая в соответствии с законом электромагнитной индукции определяется скоростью изменения магнитного потока независимо от того, чем вызвано изменение потока. В катушке, состоящей из большого числа витков, наводится э. д. с., пропорциональная скорости изменения потокосцепления, т. е. скорости изменения суммы магнитных потоков, сцепленных с отдельными витками данной катушки. Если все витки катушки пронизываются одним и тем же магнитным потоком, то, как указывалось потокосцепление равно произведению магнитного потока на число витков.
При рассмотрении цепей синусоидального тока до сих пор учитывалось явление самоиндукции, т. е. наведение э. д. с. в электрической цепи при изменении потокосцепления самоиндукции, обусловленного током в этой цепи. Отношение потокосцепления самоиндукции к току характеризовалось скалярной величиной — индуктивностью L.
Теперь нам предстоит заняться рассмотрением явления взаимной индукции, т. е. наведения э. д. с. в электрической цепи при изменении потокосцепления взаимной индукции, обусловленного током в другой электрической цепи. Цепи, в которых наводятся э. д. с. взаимной индукции, называются индуктивно связанными цепями.
Связь потокосцепления взаимной индукции одной электрической цепи с током в другой цепи, равная отношению потокосцепления взаимной индукции в одной цепи к току в другой цепи, характеризуется взаимной индуктивностью M которая, так же как и индуктивность, представляет собой скалярную величину.
Если потокосцепление
Справедливость последнего равенства можно доказать, если выразить потоки взаимной индукции 
Отсюда также видно, что величина М пропорциональна произведению чисел витков катушек и магнитной проводимости пути общего потока, которая зависит от магнитной проницаемости среды и взаимного расположения катушек.
На основании сказанного формулируется свойство взаимности для индуктивно связанных цепей: если ток, проходящий в первой цепи, обусловливает во второй цепи потокосцепление взаимной индукции 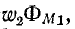
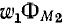
Полярности индуктивно связанных катушек эдс взаимной индукции
Напомним, что положительные направления тока и создаваемого им магнитного потока согласуются всякий раз по правилу правоходового винта. Условимся положительные направления токов 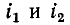
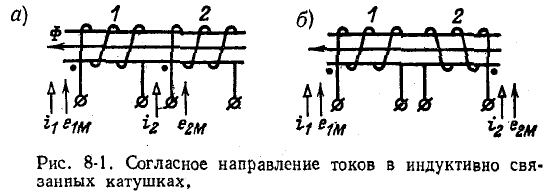
На рис. 8-1, а и б показаны индуктивно связанные катушки, насаженные на общий магнитопровод; здесь в зависимости от направления намотки витков выбраны такие положительные направления для токов 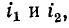
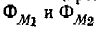
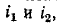
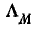
При согласном направлении токов 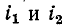
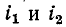
На рис. 8-1, а, где витки обеих катушек намотаны в одном направлении, одноименными выводами являются выводы, отмеченные точками (два других вывода на рис. 8-1, а составляют вторую пару одноименных выводов).
Аналогичным образом на рис. 8-1, б, где витки катушек намотаны в противоположных направлениях, одноименные выводы также отмечены точками.
Таким образом, одноименные выводы индуктивно связанных катушек характерны тем, что при одинаковом направлении токов 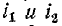
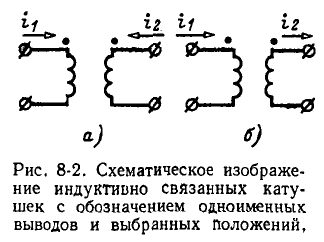
В связи с введением понятия об одноименных выводах при вычерчивании электрических схем нет необходимости показывать намотку витков индуктивно связанных катушек, а достаточно разметить на схеме их одноименные выводы. На рис. 8-2 показано схематическое изображение двух индуктивно связанных катушек с указанием одноименных выводов и выбранных положительных направлений токов 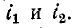
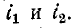
Отмечалось, что положительное направление э. д. с. самоиндукции выбирается совпадающим с положительным направлением тока; поэтому положительные
направления магнитного потока и наводимой им э. д. с. самоиндукции связаны правилом правоходового винта. Точно так же и положительное направление э. д. с. взаимной индукции 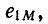
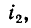
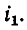
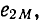
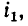
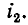
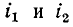
Рассмотрим случай, когда через катушку 1 проходит ток 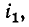
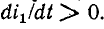
наводится э. д. с. взаимной индукции
В этом случае потенциал вывода катушки 2, одноименный с тем, в который входит ток 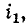
Отсюда можно заключить, что одноименные выводы двух индуктивно связанных катушек обладают той особенностью, что подведение к одной из них возрастающего тока вызывает повышение потенциала на одноименном выводе второй катушки.
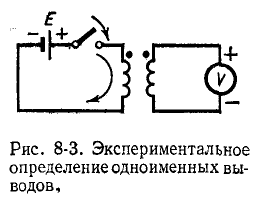
На указанном свойстве основано экспериментальное нахождение одноименных выводов индуктивно связанных катушек. Одна из них включается в цепь источника постоянного напряжения, а к другой присоединяется вольтметр постоянного тока (рис. 8-3).
Если в момент замыкания цепи источника стрелка измерительного прибора отклоняется в сторону положительных показаний, то выводы индуктивно связанных катушек, подключенные к положительному полюсу источника электрической энергии и положительному выводу измерительного прибора, являются одноименными.
Теперь рассмотрим случай встречного направления токов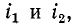
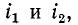
Ввиду того что положительные направления магнитных потоков самоиндукции и взаимной индукции в этом случае противоположны, э. д. с. взаимной индукции при встречном направлении токов вычисляются по формулам, содержащим знак плюс:
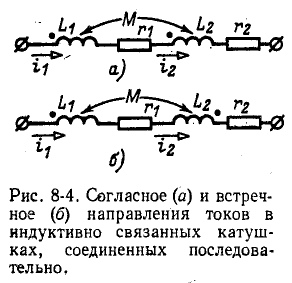
Рассмотрим последовательное соединение двух индуктивно связанных катушек (рис. 8-4, а и б).
При согласном направлении токов (рис. 8-4, а) э. д. с.
взаимной индукции 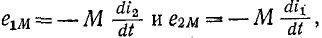
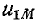
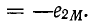
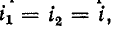
Полученное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при согласном направлении токов эквивалентны катушке, имеющей активное сопротивление 
Таким образом, как и следовало ожидать, наличие взаимной индукции при согласном направлении токов в катушках, соединенных последовательно, увеличивает индуктивность цепи.
При встречном направлении токов (рис. 8-4, б) падение напряжения от взаимной индукции при обходе контура в направлении тока получается со знаком минус:
Данное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при
встречном направлении» токов эквивалентны катушке, имеющей активное сопротивление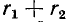
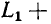
Следовательно, наличие взаимной индукции при ест речном направлении токов в катушках, соединенных последовательно, уменьшает индуктивность цепи.
На основании сказанного можно сделать следующий вывод: при согласном направлении токов падение напряжения от взаимной индукции имеет знак плюс, а при встречном — знак минус (обход цепи в обоих случаях совершается в положительном направлении тока).
Комплексная форма расчета цепи с взаимной индукцией
Представив ток в комплексной форме, получим выражение э. д. с. взаимной индукции для случая согласного направления токов в комплексной форме:
откуда комплексная действующая э. д. с. взаимной индукции
и соответственно падение напряжения от взаимной индукции
где 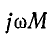
Комплексные напряжения, соответствующие (8-6) и (8-7), запишутся так:
Отсюда, между прочим, вытекает следующий способ нахождения взаимной индуктивности М: если через 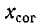
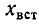
то в результате вычитания второго равенства из первого получим:
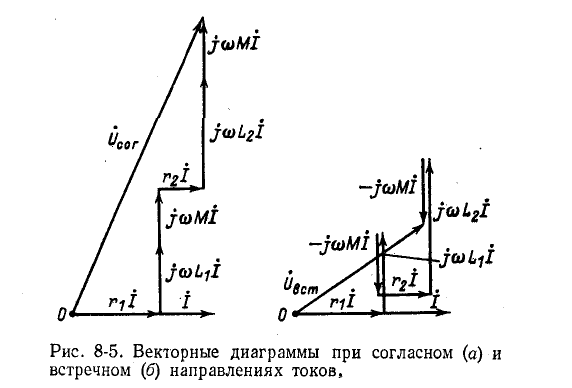
На рис. 8-5 изображены векторные диаграммы для случаев согласного и встречного направлений токов двух индуктивно связанных катушек, соединенных последовательно. При построении векторных диаграмм принято, что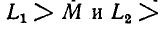
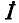
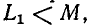
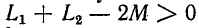
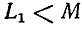
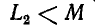
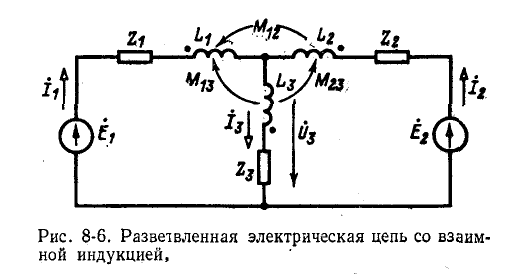
Порядок расчета разветвленных электрических цепей при наличии взаимной индуктивности иллюстрирован ниже на примере схемы рис. 8-6. Предполагается, что элементы 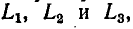
Заданными являются э. д. с. 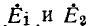
Если бы в каждом контуре был только один индуктивно связанный элемент, то запись уравнений для контурных токов не вызывала бы затруднений. В данном же случае
удобнее писать уравнения непосредственно для токов в ветвях, по первому и второму законам Кирхгофа. Совершая обход контуров по направлению токов 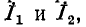
При согласном направлении токов падение напряжения в сопротивлении взаимной индукции входит со знаком плюс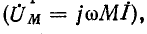
здесь 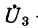
Отметим, что слагаемые с одинаковыми взаимными индуктивностями входят в уравнения с одинаковыми знаками, что может служить проверкой правильности записи уравнений.
Таким образом, расчет разветвленной электрической цепи при наличии взаимной индуктивности может быть приведен одним из описанных ранее методов с учетом падений .напряжений в сопротивлениях взаимной индукции.
Метод узловых напряжений в данном случае непосредственно неприменим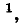
В разобранном выше примере одноименные выводы всех трех индуктивно связанных элементов были обозначены одинаково (звездочкой), так как предполагалось, что эти элементы имеют общий неразветвленный магнитопровод.
В том случае, когда три или большее число элементов располагаются на сложном, разветвленном магнитопроводе, необходимо одноименные выводы каждой пары индуктивно связанных элементов обозначать разными условными знаками (см. пример 8-2).
Пример 8-1.
Определить комплексное сопротивление на входе электрической цепи, состоящей из двух параллельно соединенных катушек, связанных индуктивно при согласном направлении токов (рис. 8-7).
Для положительных направлений контурных токов, показанных на рис. 8-7, составляем контурные уравнения:
Обозначим:
тогда
Решив уравнения относительно 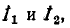
Искомое сопротивление всей цепи по отношению к выводам источника
При переключении концов одной из катушек получается параллельное соединение катушек со встречным направлением токов. В этом случае в уравнениях и конечном выражении для Z следует принять 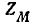
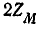
При отсутствии индуктивной связи 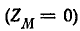
Пример 8-2.
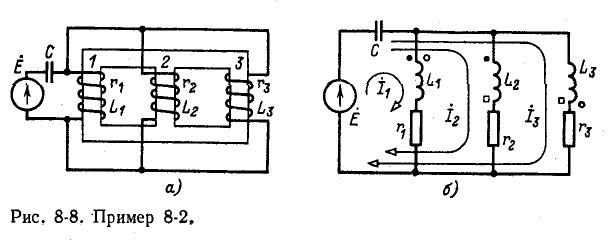
Составить уравнения контурных токов для электрической цепи, состоящей из источника э. д. с. Ё, емкости С и трех индуктивно связанных катушек, насаженных на трехстержневой магнито-провод (рис. 8-8, а). Взаимная индуктивность катушек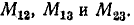
Рисунок 8-8, 6 изображает электрическую схему заданной цепи. Точками, кружками и квадратиками обозначены одноименные выводы, соответствующие каждой паре катушек.
Выбрав направления контурных токов, указанные на схеме рис, 8-8, б, составляем контурные уравнения:
Совместное решение уравнений дает токи.
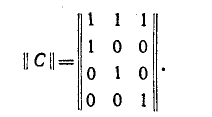
Предлагается читателям приведенную выше систему контурных уравнений получить матричным методом. Указание, Матрица соединений для схемы рис, 8-8 имеет вид:
Матрица сопротивлений ветвей равна:
Коэффициент индуктивной связи. Индуктивность рассеяния
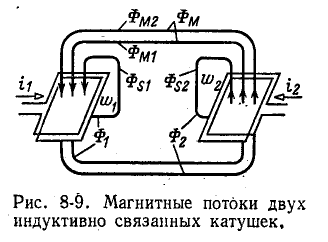
Рассмотрим картину магнитного поля индуктивно связанных катушек, схематически представленную на рис. 8-9 (для согласного направления токов).
Положим, что первая катушка состоит из витков, а вторая из 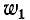
В общем случае, когда по обеим катушкам проходят токи 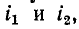
На рис. 8-9 приняты следующие обозначения магнитных потоков:
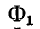
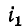
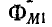
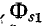
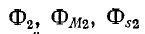
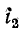
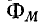
Из сказанного следует, что
Чем меньше потоки рассеяния 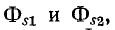
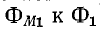
При изменении токов 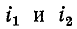
Первые слагаемые этих выражений:
называются индуктивностями рассеяния катушек.
Магнитные потоки могут быть выражены через произведения м. д. с. на магнитные проводимости путей, по которым замыкаются эти потоки:
Следовательно,
Таким образом, индуктивность катушки пропорциональна квадрату числа витков и сумме магнитных проводимостей путей потоков рассеяния и взаимной индукции.
Магнитная проводимость в свою очередь зависит от формы и размеров катушек, их взаимного расположения и магнитной проницаемости среды На основании (8-1), (8-2), (8-9) и (8-10) индуктивности рассеяния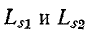
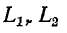
Эти выражения нам понадобятся в следующем параграфе при рассмотрении схемы замещения трансформатора.
Степень индуктивной связи двух катушек характеризуется коэффициентом связи k, определяемым как среднее геометрическое из отношений потока взаимной индукции ко всему потоку катушки, т. е.
Если выразить потоки через параметры 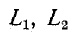
или
Из формулы (8-13) видно, что коэффициент связи всегда меньше единицы (так как 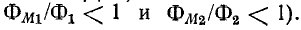
С учетом (8-3) и (8-11) коэффициент связи может быть выражен через магнитные проводимости:
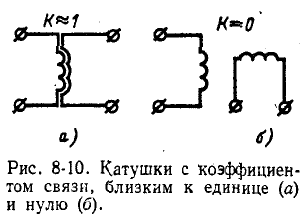
Повышение коэффициента связи достигается бифиляр-ным способом намотки катушек (рис. 8-10, а) и применением магнитопровода, так как с увеличением магнитной проницаемости и соответственно магнитной проводимости магнитопровода доля потоков рассеяния снижается.
При перпендикулярном расположении осей катушки (рис. 8-10, б) коэффициент связи обращается в нуль. Поэтому, перемещая одну катушку относительно другой, можно плавно изменять коэффициент связи в широких пределах, а при последовательном соединении этих катушек плавно изменять их результирующую индуктивность. Такое устройство называется вариометром.
При наличии магнитопровода цепь теряет свойство линейности. Однако в тех случаях, когда по условиям работы магнитная индукция в магнитопроводе не выходит за пределы прямолинейного участка кривой намагничивания и его магнитная проницаемость может быть принята постоянной, данная цепь рассматривается как линейная и изложенная выше теория сохраняет силу.
Как уже указывалось, схематическая картина магнитного поля на рис. 8-9 соответствует согласному направлению токов. Если изменить на рис. 8-9 положительное направление тока 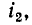
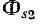
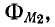
В этом случае в уравнениях, приведенных» выше, должен быть изменен знак перед 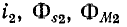
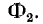
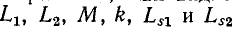
В предыдущем параграфе было показано, что при встречном направлении токов в двух катушках, соединенных последовательно, результирующая индуктивность равна
Докажем теперь, что величина 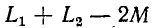
и
Заменив в первом неравенстве 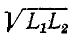
Пример 8-3.
Индуктивная катушка имеет w витков, соединенных последовательно-согласно. Индуктивность каждого витка равна L. Приняв коэффициент связи витков равным единице, определить результирующую индуктивность катушки.
При отсутствии рассеяния взаимная индуктивность каждой пары витков равна L, По аналогии с (8-6) результирующая индуктивность
катушки определится суммой индуктивностей всех витков и взаимной индуктивности, умноженной на число размещений из со витков по два:
Так как
то
Как и следовало ожидать, на основании выражений (8-11) результирующая индуктивность катушки пропорциональна квадрату числа витков,
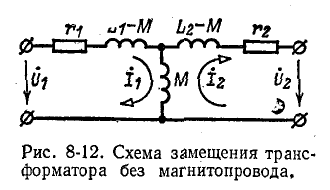
Уравнения и схемы замещения трансформатора без магнитопровода
Трансформатор представляет собой аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего предназначается для преобразования переменных напряжений и токов х. Трансформатор состоит из двух или нескольких индуктивно .связанных обмоток, насаженных на общий магнито-провод.
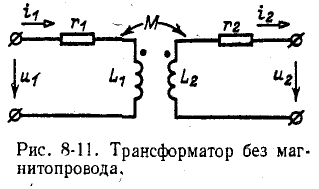
В настоящем параграфе рассматривается двухобмоточный трансформатор без Рис. 8-11. Трансформатор без маг-магнитопровода. Такой нитопровода, трансформатор может служить составной частью линейной электрической цепи в устройствах электроавтоматики, измерительной техники или связи.
Если пренебречь распределенными емкостями, существующими как между витками каждой из обмоток трансформатора, так и между самими обмотками и обмотками и землей, то трансформатор может быть представлен схемой рис. 8-11, в которой активные сопротивления обмоток условно вынесены и изображены отдельно.
1 Отсюда происходит само название «трансформатор», т. е. преобразователь.
Обмотка трансформатора, присоединяемая к источнику питания, называется первичной, а обмотка, к которой подключается нагрузка, — вторичной. Соответственно напряжения и токи на выводах этих обмоток называются первичными и вторичными. Следует заметить, что такие наименования в некоторых случаях являются условными, если в зависимости от режима энергия может передаваться, как в одну, так и в другую стороны..
При заданной полярности выводов обмоток трансформатора на схеме рис. 8-11 токи направлены встречно (что в данном случае не имеет принципиального значения).
Уравнения трансформатора в дифференциальной форме при встречном направлении токов имеют вид:
Если напряжения и токи синусоидальны, то уравнения трансформатора в комплексной форме запишутся следующим образом:
Эти уравнения равносильны следующим:
Эти уравнения равносильны следующим:
Последние уравнения являются контурными уравнениями, которые соответствуют схеме рис. 8-12.
Следовательно, эта схема может рассматриваться в качестве схемы замещения трансформатора без магнитопро-вода. В отличие от рис. 8-11 в схеме замещения первичная и вторичная цепи трансформатора связаны не индуктивно, а гальванически
Если 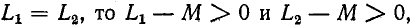
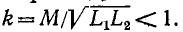
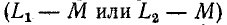
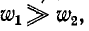
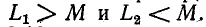
схема замещения рис. 8-12 может быть практически осуществлена только при фиксированной частоте, когда отрицательная индуктивность может быть замещена емкостным элементом; в общем же случае схема с линейным элементом, имеющим отрицательную индуктивность, практически нереализуема.
Входящие в схему рис. 8-12 разности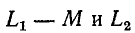
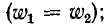
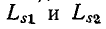
При неодинаковых числах витков первичной и вторичной обмоток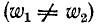
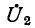
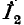
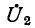
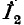
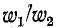
Придав уравнениям (8-15) следующий вид:
можно преобразовать их таким образом:
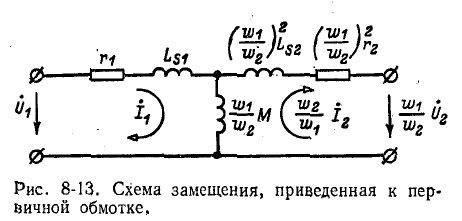
Полученные уравнения являются контурными уравнениями для приведенной схемы замещения трансформатора (рис. 8-13).
Схема замещения трансформатора, приведенная к первичной обмотке, содержит: сопротивление 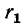
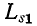
индуктивность 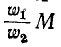
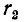
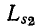
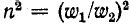
Индуктивные сопротивления 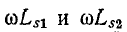
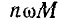
при встречном направлении токов равна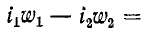
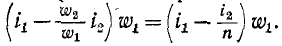
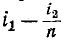
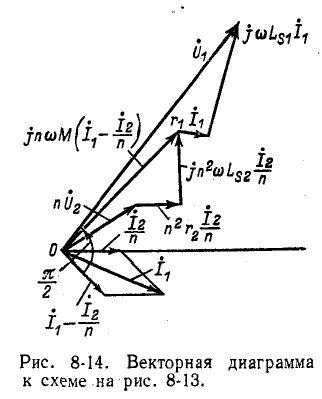
Схеме рис. 8-13 соответствует векторная диаграмма, показанная на рис. 8-14. При построении векторной диаграммы в качестве исходных могут быть приняты приведенные вторичные напряжение и ток.
Падения напряжения от приведенного вторичного тока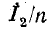
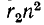
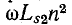
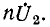
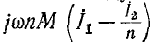
Падение напряжения от тока 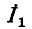
Ввиду того что вторичные электрические величины — напряжение 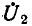
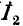
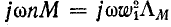
Дополнив схему рис. 8-13 идеальным трансформатором с коэффициентом трансформации n, получим эквивалентную схему трансформатора (рис. 8-15).
Рисунки 8-12—8-15 соответствуют встречному направлению токов, принятому в исходной схеме рис. 8-11.
Схема замещения с измененным положительным направлением вторичного тока соответствовала бы согласному направлению токов в исходной схеме.
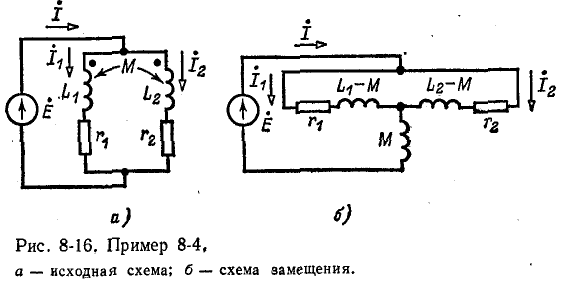
Пример 8-4.
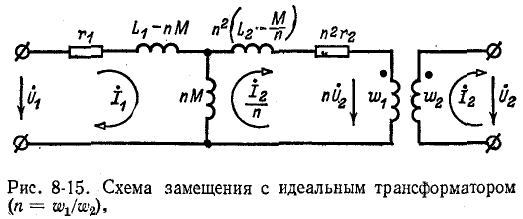
Решить пример 8-1 с помощью схемы замещения трансформатора (см. рис. 8-12).
Рассматривая индуктивно связанные элементы схемы рис. 8-16, а в качестве трансформатора с попарно соединенными первичными и вторичными выводами и пользуясь схемой замещения рис. 8-12 (с изменением направления тока 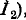
Комплексное сопротивление всей цепи равно:
Применяя сокращенную запись
находим:
Энергия индуктивно связанных обмоток
Рассмотрим вопрос об энергии индуктивно связанных обмоток. Дифференциальные уравнения двух индуктивно связанных обмоток при встречном направлении токов (см, рис, 8-11) имеют вид:
Умножив первое уравнение на 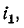
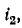
или
где 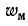
Как и следовало ожидать, мгновенная мощность,подводимая к трансформатору через первичные выводы, равна сумме мгновенных значений мощностей, расходуемых на нагрев обмоток, скорости изменения энергии 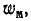
Первое слагаемое энергии магнитного поля равно энергии поля первой обмотки при

При согласном направлении токов третье слагаемое в выражении энергии будет иметь знак плюс.
Первое и второе слагаемые положительны, третье же в зависимости от знаков мгновенных токов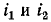
Пример 8-5.
Две индуктивно связанные катушки имеют индуктивности 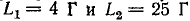
Определить энергию поля, создаваемую этими катушками при токах
Взаимная индуктивность катушек
Энергия каждой катушки, взятой отдельно, составляет:
Энергия взаимного расположения
Энергия поля всей системы при согласном направлении токов
а при встречном направлении токов
Входное сопротивление трансформатора
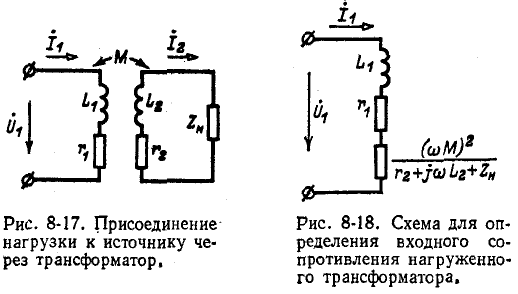
Если нагрузка 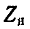
Следовательно, 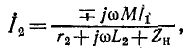
Третье слагаемое в правой части выражения (8-16) представляет собой комплексное сопротивление, вносимое из вторичной цепи в первичную; схема рис. 8-18 эквивалентна схеме рис. 8-17. В зависимости от характера 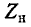
Допустим теперь, что нагрузка 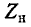
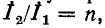
Следовательно, идеальный трансформатор, включенный между нагрузкой и источником электроэнергии, изменяет сопротивление нагрузки пропорционально квадрату коэффициента трансформации без изменения его угла.
Это свойство практически используется в различных областях электротехники, проводной связи, радио, приборостроения, автоматики для уравнивания сопротивлений источника и нагрузки (с целью повышения отдаваемой источником мощности).
Поэтому в том случае, когда требуется изменить сопротивление какой-либо нагрузки без изменения самой нагрузки, включается промежуточный трансформатор, по свойствам приближающийся к идеальному трансформатору с коэффициентом трансформации, определяемым на основании (8-17):
где 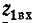
Формула (8-17) непосредственно вытекает также из приведенной схемы замещения трансформатора (см. рис. 8-13), поскольку идеальный трансформатор не имеет активных сопротивлений и индуктивностей рассеяния 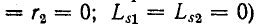
Входное сопротивление идеального трансформатора при замкнутых выходных выводах равно нулю, а при разомкнутых — бесконечности.
Пример 8-6.
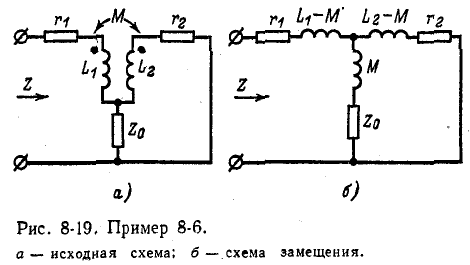
Определить входное сопротивление цепи, показанной на рис. 8-19, а.
Пользуясь схемой замещения, представленной на рис. 8-19, б, находим:
Пример 8-7.
Определить входное сопротивление цепи, состоящей из двух трансформаторов, включенных каскадно с нагрузкой 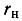
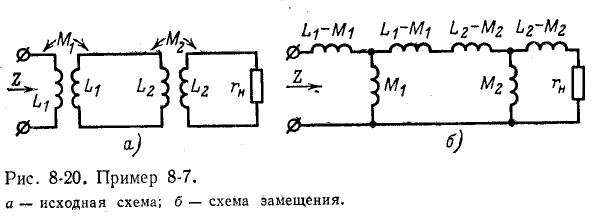
В соответствии с (8-16) входное сопротивление второго трансформатора будет:
Рассматривая 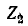
После преобразования находим:
К тому же результату можно прийти на основе схемы замещения, показанной на рис. 8-20, б.
Автотрансформатор
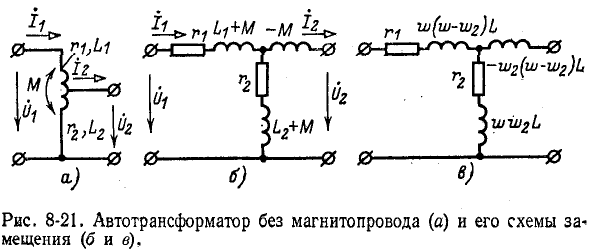
Автотрансформатор отличается от трансформатора тем, что его обмотка низшего напряжения является частью обмотки высшего напряжения (рис. 8-21, а). Так же как и трансформатор, он может быть понижающим или повышающим.
Уравнения автотрансформатора в комплексной форме для указанных на рис. 8-21, а положительных направлений токов и напряжений записываются так:
Эти уравнения соответствуют схеме замещения, показанной на рис. 8-21, б. Правая ветвь схемы состоит из практически неосуществимого линейного элемента — отрицательной индуктивности (—М). Поэтому полученная схема замещения рис. 8-21, б может быть использована только для расчета. Практически осуществить ее можно только для фиксированной частоты, когда элемент — М
замещается емкостью. Однако если индуктивность нагрузки, подключенной к выходным выводам, компенсирует отрицательную индуктивность, то схема замещения автотрансформатора в сочетании с нагрузкой практически осуществима.
Итак, схема замещения автотрансформатора представляет собой трехлучевую звезду. Сопротивления лучей этой звезды могут быть найдены и другим способом, если поочередно приравнять суммы сопротивлений двух лучей сопротивлениям между соответствующими выводами автотрансформатора (при разомкнутом трётьем выводе).
Обозначим: индуктивность каждого витка L, общее число витков 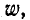
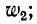
В режиме холостого хода автотрансформатора (т. е. при разомкнутых выходных выводах), если не учитывать рассеяния, отношение первичного напряжения 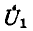
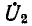
n — коэффициент трансформации автотрансформатора.
При нагрузке подводимая к автотрансформатору мощность передается на вторичную сторону как посредством электромагнитной индукции (через магнитное поле), так и непосредственно через электрическую связь.
Применение автотрансформатора вместо обычного трансформатора той же мощности и с таким же коэффициентом трансформации дает экономию в меди, затрачиваемой на обмотку. Экономия достигается за счет сокращения общего числа витков и уменьшения толщины провода обмотки, через которую проходит ток, равный разности первичного и вторичного токов.
Экономия в меди тем больше, чем ближе к единице коэффициент трансформации, так как при этом уменьшается разность токов
Индуктивно связанные колебательные контуры
В радиотехнике широко распространены двухконтурные колебательные системы, в которых связь между контурами осуществляется при помощи взаимной индукции.
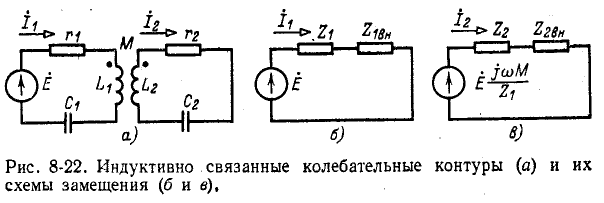
На рис. 8-22, а показаны колебательные контуры с индуктивной (трансформаторной) связью. Обозначим собственные сопротивления контуров через 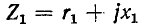
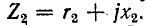
На рис. 8-22, б изображена схема замещения для первичного контура. Первичный ток равен:
а вторичный ток
Следует заметить, что напряжение 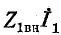
Подставив (8-18) в (8-19) и умножив числитель и знаменатель на 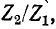
Выражение (8-20) могло быть выведено и по теореме об эквивалентном источнике.
Числитель полученной дроби равен э. д. с., наводимой во вторичном контуре, когда он разомкнут, а знаменатель представляет собой эквивалентное сопротивление вторичного контура, в котором влияние первичного контура учтено сопротивлением 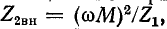
Схема замещения для вторичного контура показана на рис. 8-22, в; здесь
Активные составляющие вносимых сопротивлений всегда положительны, а знаки реактивных составляющих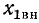
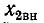
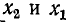
Как 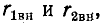
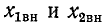
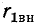
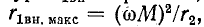
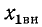
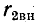
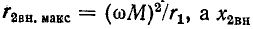
Настройка связанных контуров
На практике часто добиваются получения максимального тока 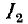
- изменением параметров первичного контура, например емкости
, резонанс, который при этом возникает, называется первым частным резона н-с о м;
- изменением параметров вторичного контура, например емкости
; в этом случае возникает второй частный резонанс;
- изменением параметров одного из контуров и сопротивления связи; резонанс в этом случае называется сложным;
- изменением параметров обоих контуров и сопротивления связи; в этом случае резонанс называется полным.
Первый частный резонанс:
Согласно (8-19) вторичный ток прямо пропорционален первичному. Поэтому максимуму тока 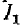
Первый частный резонанс наступает при
В этом случае:
Второй частный резонанс наступает при
При этом
Сложный резонанс:
При настройке первичного контура оптимальное сопротивление связи найдем, приравняв нулю первую производную
Отсюда
Следовательно, оптимальное сопротивление связи
‘ В этом случае получается максимум максиморум вторичного тока:
Условия (8-21) и (8-23), которые при этом выполняются, означают, что собственное сопротивление первичного контура равно сопротивлению, комплексно сопряженному с сопротивлением, вносимым из вторичного контура в первичный, т. е.
Из [формулы (3-17)] известно, что это и есть условие передачи максимума активной мощности от источника к приемнику.
Аналогично при настройке вторичного контура оптимальное сопротивление связи равно:
причем условия (8-22) и (8-24) в совокупности означают,
что
т. е. и в этом случае выполняется условие передачи максимума активной мощности от источника к приемнику. При этом
Следовательно, при сложном резонансе максимум максиморум вторичного тока не зависит от того, какой из контуров настраивается на резонанс.
Полный резонанс:
При настройке на полный резонанс сначала настраивают первичный контур при разомкнутом вторичном, т. е. добиваются условия 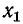
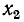
Оптимальное сопротивление связи находится из условия
откуда
При этом вторичный ток равен:
Хотя максимум максиморум вторичного тока при настройке на полный резонанс и получается таким же, как при настройке на сложный резонанс, настройка на полный резонанс имеет то преимущество, что сопротивление связи меньше, чем при сложном резонансе, оно как и активные сопротивления 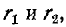
Эффективность передачи энергии из первичного контура во вторичный оценивается коэффициентом полезного действия двухконтурной системы, равным отношению мощности, поглощаемой сопротивлением 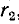
Очевидно, 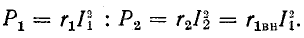
Когда вторичный контур настроен на частоту источника,
При настройке на полный резонанс 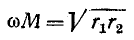
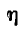
Если колебательные контуры идентичны и частота близка к резонансной, то оптимальный коэффициент связи при настройке на полный резонанс с учетом (8-25) примерно равен затуханию контура:
Например, для радиотехнических контуров с добротностью Q = 100 оптимальный коэффициент связи составит
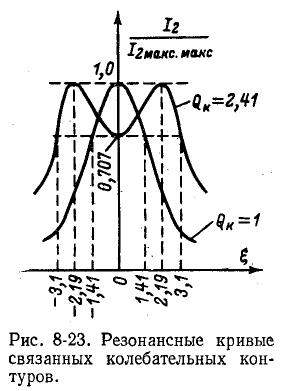
Резонансные кривые и полоса пропускания связанных контуров
Ограничимся рассмотрением случая, когда связанные колебательные контуры имеют одинаковые резонансную частоту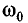
Для построения резонансных кривых вторичного тока воспользуемся выражением (8-20), приняв 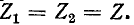
Величина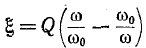
При частотах, близких к резонансной, 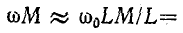
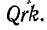
откуда
Отнеся вторичный ток к току 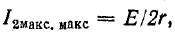
Если контуры настроены на частоту источника, то 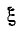
Выясним, каким значениям 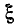
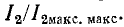
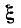
При Qk < 1 второй и третий корни лишены физического смысла и резонансная кривая имеет только один максимум — при 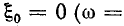
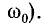
При Qk = 1 и 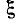
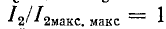
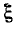
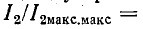
Сказанное иллюстрируется рис. 8-23.
Легко показать, что при 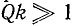
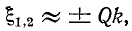
Коэффициент связи k = 1/Q = d, при котором получается предельная одногорбая резонансная кривая, называется критическим. Он совпадает с оптимальным коэффициентом связи двух идентичных контуров, настроенных на полный резонанс.
Полосой пропускания связанных колебательных контуров, как и в случае одиночного колебательного контура, условно считается область частот, на границах которой резонансная кривая снижается не более чем в 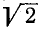
Так как
то приняв вблизи резонансной частоты
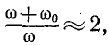
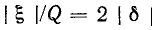
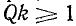
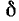
служит
Это выражение справедливо до тех пор, пока впадина резонансной кривой находится выше или совпадает c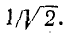
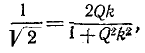
Подставив это значение Qk в (8-28), найдем:
т. е. при Qk = 2,41 полоса пропускания в 3,1 раза больше, чем у одиночного колебательного контура.
Если Qk = 1, то 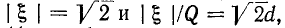
При Qk = 0,68 полоса пропускания связанных контуров равна полосе пропускания одиночного контура, а при 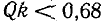
Величина Qk в радиотехнической литературе носит название параметра связи.
(8-28)
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Теорема об эквивалентном источнике
- Применение матриц к расчету электрических цепей
- Дуальные цепи
- Электромеханические аналогии
5.1 Индуктивная связь. Эдс взаимной индукции. Взаимная индуктивность. Коэффициент связи.
Электрические
цепи называются связанными, если процессы
в них влияют друг на друга. Это влияние
может осуществляться посредством
общего электрического или магнитного
поля. В последствии случая цепи называются
индуктивно связанными.
Рассмотрим две
катушки, расположенные рядом (рис. 5.1.а)
Рис.5.1
Протекающий в
первой катушке с числом витков
W1и индуктивностиL1токi1вызывает
магнитный поток Ф11. Часть потока
Ф12охватывает находящуюся вторую
катушку с числом витковW2и индуктивностьюL2.
ЭДС, находящаяся
в первой катушке под воздействием Ф11
называется ЭДС
самоиндукции, где
— потокосцепление самоиндукции ………………
,
где
-потокосцепления взаимной индукции,
-взаимная
индуктивность между первой и второй
катушками.
Протекающий во
второй катушке ток i2(рис.5.1.б), вызывает поток Ф22.
Часть этого потока,
охватывает витки первой катушки. По
аналогии можем записать
,
,
где e2-ЭДС
самоиндукции второй катушки,
-потокосцепление
самоиндукции второй катушки,
e21-ЭДС
взаимной индукции, находящаяся в первой
катушке под воздействием потока Ф21.
М21-взаимная
индуктивность между второй и первой
катушками.
Если обе катушки
находятся в среде не обладающей никакими
аномальными свойствами, то взаимные
индуктивности М12и М21оказываются равными
М12=М21=М.
величина и по ней
трудно судить о степени взаимного
влияния катушек друг на друга.
Для оценки степени
связи катушек пользуются относительной
величиной –коэффициентом связи К,
который определяется как среднее
геометрическое из отношения потокосцепления
взаимной индукции к потокосцеплениям
самоиндукции.
Коэффициент К
может принимать значения в пределах от
0 до 1.
При К=0 между
катушками не существует индуктивной
связи, при К=1-поток одной катушки
полностью охватывает витки второй
катушки Ф12=Ф11, Ф21=Ф22.
Величина К зависит
от:
–расстояния
между катушками,
–взаимной
ориентации катушек в пространстве,
–магнитных
свойств среды, в которой расположены
катушки.
5.2. Одноименные зажимы индуктивно связанных катушек.
Рассмотрим две
катушки, расположенные на одном основании
(рис 5.2)
Рис. 5.2
Направление тока
и вызванного им магнитного потока
связаны по правилу правого винта.
Следовательно ток i1будет вызывать поток Ф1,направленный
влево. Токi2будет
вызывать магнитный поток Ф2,также
направленный влево.
Т.е. зажимы
индуктивно связанных катушек, одинаковое
направление токов относительно которых,
вызывает одинаковое направление потоков
–называются одноименными. На электрических
схемах цепей одноименные зажимы катушек
принято обозначать жирными точками или
звездочками.
5.3. Последовательное соединение индуктивно связанных катушек при согласном включении.
Рассмотрим две
индуктивно связанные катушки, соединенные
последовательно (рис 5.3). Каждая из
катушек обладает индуктивностью L1иL2и активным
сопротивлением проводника из которого
катушка изготовленаr1иr2. Индуктивная
связь на электрической
схеме указана двусторонней стрелкой и
взаимной индуктивностью М.
Рис 5.3.
Одноименные зажимы
катушек обозначены жирными точками и
расположены так, что протекающий под
воздействием напряжения U
ток I
вызывает в катушках одинаковое направление
потоков. Поэтому включение называется
согласным.
Запишем уравнение
представленное на рис 5.3 цепи мгновенных
значениях токов и напряжений.
Для комплексов
действующих значений токов и напряжений
последнее уравнение примет вид:
Перепишем это
уравнение следующим образом:
Выражение в
квадратных скобках называется
сопротивлением двух последовательно
соединенных индуктивно связанных
катушек при согласном включении
Выражение в круглых
скобках называется полной индуктивностью
двух последовательно соединенных
индуктивно связанных катушек при
согласном включении
Очевидно Zсогл
>Z,
где Z-полное
сопротивление двух последовательно
соединенных катушек без индуктивной
связи:
Увеличение
сопротивления Zсоглпроисходит за счет увеличения полной
индуктивностиLсогл
Построим векторную
диаграмму двух последовательно
соединенных индуктивно связанных
катушек при согласном включении. Для
этого задаемся вектором
тока
.
Напряжение на активном сопротивлении
первой катушкисовпадает по фазе с током. Напряжение
на индуктивности первой катушкиопережает ток на 900. Откладываем
этот вектор с конца векторапод прямым углом к
току
.
Напряжение на первой катушке, вызванное
индуктивной связью
также опережает
ток на 900. Откладываем этот вектор
с конца вектора.
Напряжение на активном сопротивлении
второй катушкисовпадает с током
.
Напряжение на второй индуктивностии напряжение на второй катушке
обусловленное взаимной индуктивностьюопережает ток на 900.
Откладываем
вектора напряжения в таком же порядке
: следующий вектор откладывается с конца
предыдущего.
В результате
получим векторную диаграмму изображенную
на рис 5.4.
Рис.5.4
Соединяя начало
вектора
и конец последнего вектора
,
получим напряжение.
Сумма первых трех векторов напряжения
дает напряжение на первой катушке.
Напряжение на второй катушке,
получается как сумма последних трех
векторов напряжения.
Соседние файлы в папке Конспект 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
Random converter
- Калькуляторы
- Электротехнические и радиотехнические калькуляторы
Калькулятор взаимной индукции
Этот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности.
Пример. Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока.
Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле:
где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. У слабо связанных катушек или обмоток коэффициент связи k < 0.5. У сильно связанных катушек коэффициент связи k > 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
Тороидальные трансформатор и дроссель в импульсном блоке питания
Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как
Две катушки с взаимной индукцией на принципиальной схеме
При увеличении силы тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь. Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания
В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока
Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
Примеры расчетов
Расчет взаимоиндукции двух катушек индуктивности 110 микрогенри и 130 микрогенри с коэффициентом связи 0,5
Расчет взаимоиндукции двух катушек индуктивности 10 мГн и 12 мГн с коэффициентом связи 0,25
Расчет взаимоиндукции двух катушек индуктивности 20 микрогенри и 24 микрогенри с коэффициентом связи 0,5
Расчет взаимоиндукции двух катушек индуктивности 12 миллигенри и 15 миллигенри с коэффициентом связи 0,75
Расчет взаимоиндукции двух катушек индуктивности 8,2 миллигенри и 10 миллигенри с коэффициентом связи 0,5
Расчет взаимоиндукции двух катушек индуктивности 430 микрогенри и 510 микрогенри с коэффициентом связи 0,25
Расчет взаимоиндукции двух катушек индуктивности 1 мГн и 1,2 мГн с коэффициентом связи 0,25
Расчет взаимоиндукции двух катушек индуктивности 100 мГн и 120 мГн с коэффициентом связи 0,25
Расчет взаимоиндукции двух катушек индуктивности 560 миллигенри и 680 миллигенри с коэффициентом связи 0,25
Расчет взаимоиндукции двух катушек индуктивности 56 миллигенри и 68 миллигенри с коэффициентом связи 0,25
Электротехнические и радиотехнические калькуляторы
Электроника — область физики и электротехники, изучающая методы конструирования и использования электронной аппаратуры и электронных схем, содержащих активные электронные элементы (диоды, транзисторы и интегральные микросхемы) и пассивные электронные элементы (резисторы, катушки индуктивности и конденсаторы), а также соединения между ними.
Радиотехника — инженерная дисциплина, изучающая проектирование и изготовление устройств, которые передают и принимают радиоволны в радиочастотной области спектра (от 3 кГц до 300 ГГц), также обрабатывают принимаемые и передаваемые сигналы. Примерами таких устройств являются радио- и телевизионные приемники, мобильные телефоны, маршрутизаторы, радиостанции, кредитные карточки, спутниковые приемники, компьютеры и другое оборудование, которое передает и принимает радиосигналы.
В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Главная
→
Теория электрических цепей
→
Коэффициент связи
Коэффициент связи
Коэффициент связи — отношение взаимной индуктивности к ее максимально возможному значению (при отсутствии потоков рассеивания в индуктивно-связанных катушках)
k μ = k СВ = | M | M max = | M | L 1 L 2 ≤1,
где L1, L2 — индуктивности самоиндукции индуктивно-связанных катушек (например, L1 = N1Ф11/i1), при этом коэффициент связи kСВ = 1 соответствует так называемой совершенной магнитной связи, когда равны нулю индуктивности рассеяния.

индуктивно-связанные катушки
Беспроводная передача энергии через магнитно-связанные индуктивные катушки
Время на прочтение
6 мин
Количество просмотров 27K
Введение
Думаю, что многие из читателей видели хотя бы один ролик на популярных видеосервисах, где электричество передается через пустое пространство при помощи индуктивных катушек.
В этой статье мы хотим обратиться к первоосновам процесса беспроводной передачи энергии с помощью магнитного поля. Начав с рассмотрения простейшей индуктивной катушки, и вычисления ее индуктивности, мы постепенно перейдем к теории электрических цепей, в рамках которой, будет показан и обоснован способ
передачи максимальной мощности
при прочих равных условиях. Итак, начнем.
Магнитное поле одиночного витка с током
Рассмотрим магнитное поле одиночного витка с током. Найдем магнитное поле витка в любой точке пространства. Почему необходимо подобное рассмотрение? Потому что почти во всех книгах, по крайней мере в тех, которые удалось отыскать автору статьи, решение данной задачи ограничивается нахождением лишь одной компоненты магнитного поля и лишь вдоль оси витка —
, в то время как мы отыщем закон для магнитного поля во всем пространстве.
Иллюстрация к закону Био-Савара-Лапласа
Для нахождения магнитного поля, воспользуемся законом Био-Савара-Лапласа (смотри Википедия — Закон Био-Савара-Лапласа). На рисунке видно, что центр системы координат
совпадает с центром витка. Контур окружности витка обозначен как
, а радиус окружности — как
.По витку течет ток
.
— это переменная-радиус-вектор из начала координат в произвольную точку витка.
— это радиус-вектор в точку наблюдения. Еще нам понадобится полярный угол
— угол между радиус-вектором
и осью
. Расстояние от оси витка до точки наблюдения обозначим за
. И наконец,
— элементарное приращение радиус-вектора
.
Согласно закону Био-Савара-Лапласа, элемент контура с током
создает элементарный вклад в магнитное поле, который дается формулой
Теперь остановимся подробнее на переменных и выражениях, входящих в формулу. С учетом аксиальной симметрии задачи можем записать
Для того чтобы найти результирующее магнитное поле, нужно проинтегрировать по всему контуру витка, то есть
После подстановки всех выражений и некоторых тождественных преобразований получаем выражения для аксиальной и радиальной компоненты магнитного поля соответственно
Для нахождения абсолютного значения магнитного поля необходимо просуммировать компоненты по теореме Пифагора
.
Продемонстрируем полученное решение на примере витка радиуса
(м) и
(А).
Амплитуда аксиальной компоненты магнитного поля
Амплитуда радиальной компоненты магнитного поля
Абсолютная амплитуда магнитного поля
Заметим, что для витка произвольной формы, на больших расстояниях
, т.е. много больше характерного размера витка, поведение магнитного поля будет стремиться к найденному решению.
Подсказка…
Для подобных вычислений и построения графиков удобно использовать MathCad 15
Катушка индуктивности. Магнитно-связанные катушки
Теперь, когда мы знаем решение для магнитного поля одного витка, можем найти индуктивность катушки, состоящей из
витков. По определению индуктивность — это коэффициент пропорциональности между током в витке и магнитным потоком через площадь сечения витка. Мы пользуемся здесь идеальной моделью катушки, которая безразмерна по направлению своей оси симметрии. Конечно же, на практике такого не бывает. Однако, как приближенные, полученные формулы будут достаточно хороши. Хотя катушки и считаются безразмерными вдоль
, необходимо задаться ненулевым радиусом сечения провода. Обозначим его
, и пример равным
(мм). Иначе при интегрировании магнитного потока подынтегральное выражение обратится в бесконечность.
Индуктивно связанные катушки
На рисунке изображены две магнитно связанные катушки. Пусть первая катушка имеет радиус
и содержит
витков, а вторая —
и
соответственно. Тогда для нахождения собственных индуктивностей необходимо вычислить магнитный поток каждой катушки через свое собственное сечение.
Поскольку в катушке много витков, найдем величину, называемую потокосцепление, дважды умножив на количество витков
По определению, индуктивность это коэффициент пропорциональности
в формуле
. Таким образом, получим собственные индуктивности катушек
Пусть центры катушек разделены расстоянием
, лежат на одной оси, и их плоскости витков сориентированы параллельно. Для нахождения взаимной индуктивности, нужно вычислить потокосцепление, образуемое одной катушкой через сечение другой, то есть
Тогда взаимная индуктивность катушек дается выражением
Насколько известно автору, такие интегралы можно взять только численно.
Заметим, что как правило
и
. Коэффициентом связи катушек называется величина
Исследуем зависимость коэффициента связи катушек от расстояния. Для этого рассмотрим две одинаковые катушки с радиусом витков
(м) и количеством витков
. При этом собственная индуктивность каждой из катушек составит
(мГн).
Коэффициент связи катушек от расстояния между ними
График не изменится, если одинаково изменить число витков в обеих катушках, либо одинаково изменить радиус обеих катушек. Коэффициент связи удобно выражать в процентах. Из графика видно, что даже при расстоянии между катушками в 1 (мм) коэффицент связи меньше 100%. Коэффициент падает до 10% на расстоянии порядка 60 (мм), и до 1% на 250 (мм).
Беспроводная передача энергии
Итак, нам известны индуктивности и коэффициент связи. Теперь воспользуемся теорией электрических цепей переменного тока для поиска оптимальных параметров, при которых передаваемая мощность оказалась бы максимальной. Для понимания этого параграфа читатель должен быть знаком с понятием электрического импеданса, а также с законами Кирхгофа и законом Ома. Как известно из теории цепей, две индуктивно-связанные катушки образуют воздушный трансформатор. Для анализа трансформаторов удобна Т-образная схема замещения.
Воздушный трансформатор и его эквивалентная схема
Передающую катушку слева будем условно называть «трасмиттер», а принимающую катушку справа — «ресивер». Между катушками коэффициент связи
. На стороне ресивера находится потребитель, представленный нагрузкой
. Нагрузка в общем случае может быть комплексной. Входное напряжение на стороне трансмиттера
, а входной ток —
. Напряжение, передаваемое на ресивер —
, и передаваемый ток
. Полный импеданс на стороне трансмиттера обозначим как
, а полный импеданс на стороне ресивера
.
Предполагается, что на вход схемы подается синусоидальное напряжение
.
Обозначим
— сопротивления и индуктивности катушек (две собственные и одна взаимная) соответственно. Тогда, согласно теории трансформатора
С другой стороны, согласно нашим обозначениям
где
— полные
активные
сопротивления на стороне трансмиттера и ресивера соответственно, и
— полные
реактивные
сопротивления.
Импеданс связи равен
.
Найдем входной ток цепи
где знак
обозначает параллельное соединение сопротивлений. Тогда напряжение, переданное на ресивер
И наведенный ток
Можем найти комплексную мощность, переданную в ресивер
Таким образом имеем выражение для комплексной мощности
Выражение для
активной
компоненты мощности
Выражение для
реактивной
компоненты мощности
В большинстве практических задач требуется передать максимальную активную мощность, поэтому
Либо, что то же самое
Для удобства введем функцию
и исследуем ее на наличие экстремумов
Откуда получаем систему из двух уравнений
Эта система имеет пять решений, два из которых нефизичны, так как приводят к мнимым значениям величин, которым полагается быть действительными. Три других
физических
решения приведены ниже вместе с соответствующими формулами для мощности
Решение 1
Мощность
Решение 2 и 3
Мощность для решений 2 и 3
Решение 2 и 3 нужно использовать, когда реактивное сопротивление связи достаточно велико
Когда же это не так, нужно использовать решение 1. Чаще всего в реальных ситуациях
окажется мало, поэтому рассмотрим решение 1 несколько подробнее.
Решение 1:
. И соответствующая ему активная мощность дается формулой
Из формулы мощности видно, что мощность зависит от реактивного сопротивления связи
, а значит и от частоты передачи
, и от геометрии взаимного расположения катушек, которая учитывается коэффициентом связи
.
Как заметили внимательные читатели, зависимость
— нелинейная. Функция
достигает максимума при
.
Исследование формулы мощности на экстремумы
Максимальная активная мощность при
равна
Таким образом, вышеозначенная формула представляет
абсолютный теоретический предел
переданной активной мощности при любых условиях. При этом для реактивной мощности, переданной в ресивер, имеем
Численное моделирование
Продемонстрировать работу всей вышеизложенной теории можно, выполнив симуляцию SPICE модели нашего устройства из двух связанных катушек.
SPICE модель двух индуктивно-связанных катушек
Симуляция выполнена для коэффициента связи
%, что соответствует 25 см удаления между катушками. Параметры катушек те же, что и в предыдущем параграфе, принятые для построения графика
.
Получается, что реактивные сопротивления каждой из катушек необходимо скомпенсировать конденсаторами
и
. То есть настроить каждый из контуров (передающий и принимающий) в резонанс на заданной частоте. Если предположить, что величина нагрузки действительная, то величины емкостей могут быть найдены из формул
Ниже приведены два графика для переданного напряжения и переданной мощности во времени на частоте
(кГц).
Переданное напряжение
Переданная мощность
Из рисунков видно, что на расстоянии 25 (см) переданное напряжение оказалось приблизительно в 2.5 меньше входного, а переданная пиковая мощность — приблизительно в 4 раза меньше мощности, потребляемой от входа,
что согласуется с полученными формулами
.
В заключении опишем, какие меры можно предпринять для увеличения передаваемой мощности:
- увеличить количество витков в катушках
- увеличить радиус витков
- увеличить частоту передачи
- уменьшить расстояние между катушками
- ввести магнитный сердечник, принадлежащий обеим катушкам (замкнутый либо открытый)
- ввести незамкнутый магнитный сердечник, принадлежащий лишь катушке-ресиверу
Пожалуй, написание этой статьи накладывает на автора обязательство изготовить и протестировать такую систему из двух катушек в лабораторных условиях, но это уже совсем другая история. Благодарю за внимание.
Литература
- Сивухин, Д. В. «Общий курс физики. Т. 3: Электричество и магнетизм.» (1990).
- Бессонов, Лев Алексеевич. Теоретические основы электротехники. Электромагнитное поле. Общество с ограниченной ответственностью Издательство ЮРАЙТ, 2012.
- Лаврентьев, М. А., and Б. В. Шабат. «Теория функций комплексной переменной.» (1972).

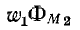
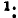
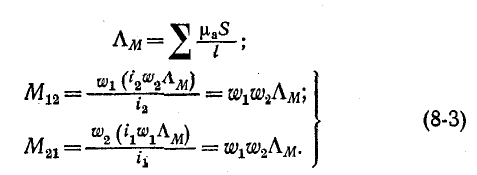
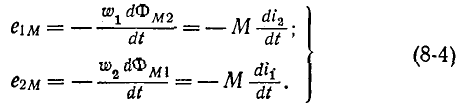
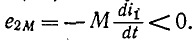
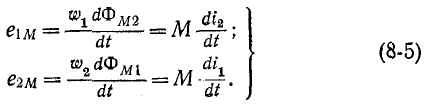
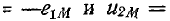
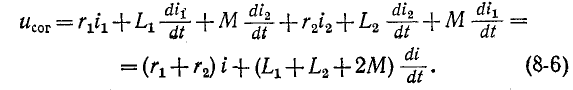
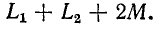
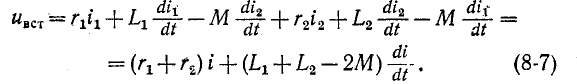
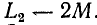
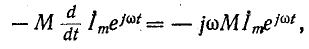
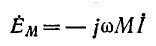
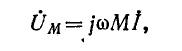
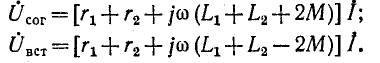
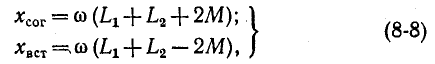
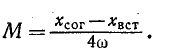
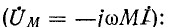
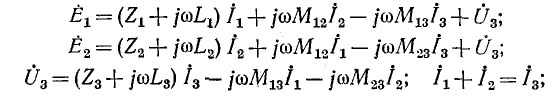

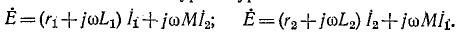
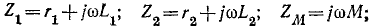
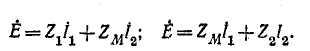
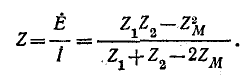
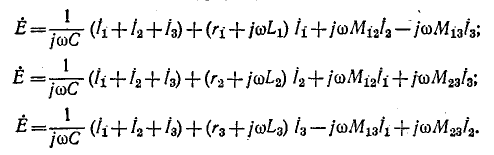
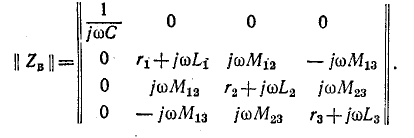
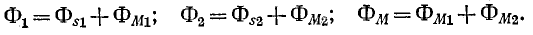
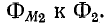
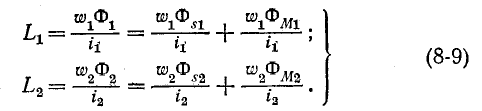
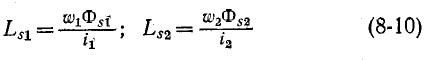
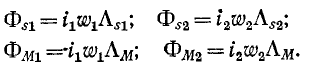
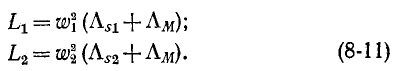
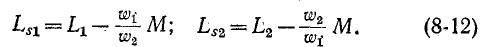
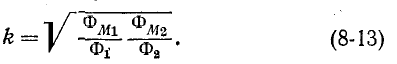
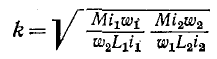

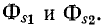
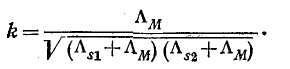
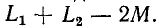
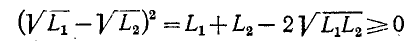
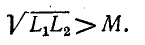
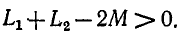
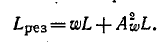
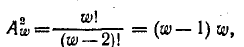
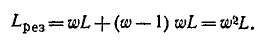
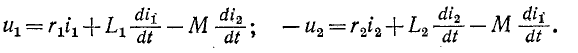
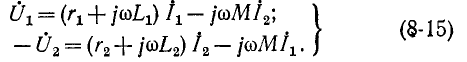
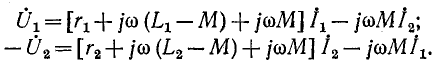
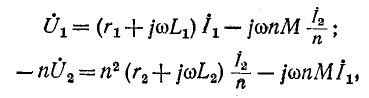
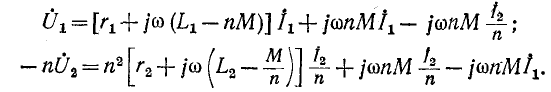
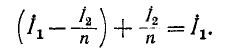
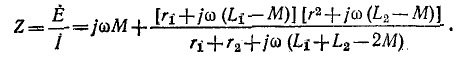
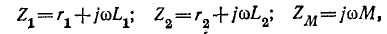
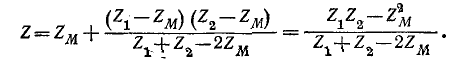
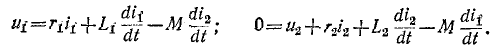
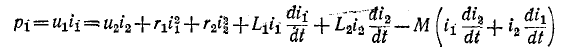
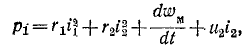
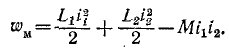
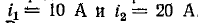
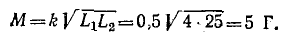
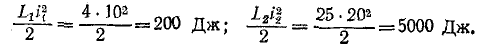
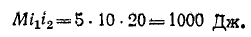
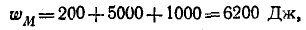
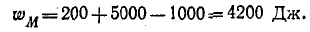
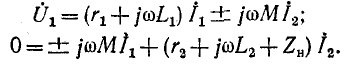
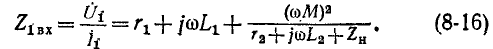
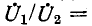
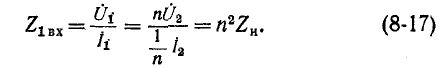
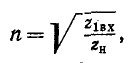
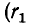
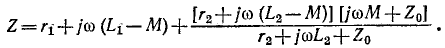
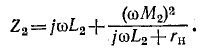
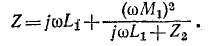
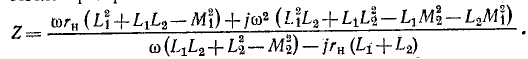
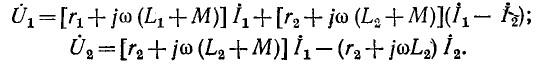
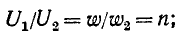
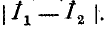
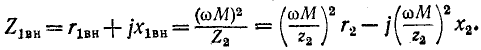


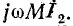
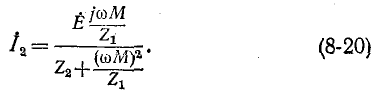
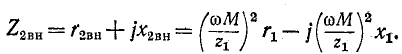
 , резонанс, который при этом возникает, называется первым частным резона н-с о м;
, резонанс, который при этом возникает, называется первым частным резона н-с о м;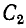 ; в этом случае возникает второй частный резонанс;
; в этом случае возникает второй частный резонанс;