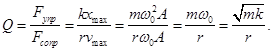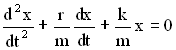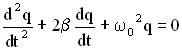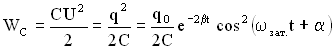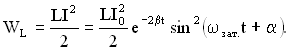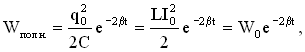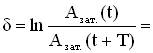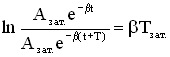Затухающие
колебания. Декремент затухания,
коэффициент затухания, время релаксации
Свободные колебания
технических систем в реальных условиях
протекают, когда на них действуют силы
сопротивления. Действие этих сил приводит
к уменьшению амплитуды колеблющейся
величины.
Колебания,
амплитуда которых из-за потерь энергии
реальной колебательной системы
уменьшается с течением времени,
называются затухающими.
Наиболее часто
встречается случаи, когда сила
сопротивления пропорциональна скорости
движения
где r —
коэффициент сопротивления среды. Знак
минус показывает, что FC направлена
в сторону противоположную скорости.
Запишем
уравнение колебаний в точке, колеблющийся
в среде, коэффициент сопротивлений
которой r. По
второму закону Ньютона
где β — коэффициент
затухания. Этот коэффициент характеризует
скорость затухания колебаний, При
наличии сил сопротивления энергия
колеблющейся системы будет постепенно
убывать, колебания будут затухать.
— дифференциальное
уравнение затухающих колебаний.
— уравнение
затухающих колебаний.
ω – частота затухающих
колебаний:
Период затухающих
колебаний:
З
колебания при строгом рассмотрении не
являются периодическими. Поэтому о
периоде затухаюших колебаний можно
говорить, когда β мало.
Если
затухания выражены слабо (β→0), то .
Затухающие колебания можно
рассматривать как
гармонические колебания, амплитуда
которых меняется по экспоненциальному
закону
В
уравнении (1) А0 и
φ0 —
произвольные константы, зависящие от
выбора момента времени, начиная е
которого мы рассматриваем колебания
Рассмотрим
колебание в течение, некоторого времени
τ, за которое амплитуда уменьшится
в е раз
τ — время релаксации.
Коэффициент
затихания β обратно пропорционален
времени, в течение которого амплитуда
уменьшается в е раз.
Однако коэффициента затухания недостаточна
для характеристики затуханий колебаний.
Поэтому необходимо ввести такую
характеристику для затухания колебаний,
в которую входит время одного колебаний.
Такой характеристикой
является декремент (по-русски:
уменьшение) затуханияD,
который равен отношению амплитуд,
отстоящих по времени на период:
Логарифмический
декремент затухания равен
логарифму D:
Логарифмический
декремент затухания обратно пропорционален
числу колебаний, в результате которых
амплитуда колебаний уменьшилась
в е раз.
Логарифмический декремент затухания
— постоянная для данной системы величина.
Еще
одной характеристикой колебательной
система является добротность Q.
Добротность
пропорциональна числу колебаний,
совершаемых системой, за время релаксации
τ.
Добротность Q колебательной
системы является мерой относительной
диссипации (рассеивания) энергии.
Добротность Q колебательной
системы называется число, показывающее
во сколько раз сила упругости больше
силы сопротивления.
Чем больше добротность,
тем медленнее происходит затухание,
тем затухающие колебания ближе к
свободным гармоническим.
Вынужденные
колебания.
Резонанс
В целом ряде случаев
возникает необходимость создания
систем, совершающих незатухающие
колебания. Получить незатухающие
колебания в системе можно, если
компенсировать потери энергии,
воздействуя на систему периодически
изменяющейся силой.
Пусть
Запишем
выражение для уравнения движения
материальной точки, совершающей
гармоническое колебательное движение
под действием вынуждающей силы.
По второму закону
Ньютона:
(1)
— дифференциальное
уравнение вынужденных колебаний.
Это дифференциальное
уравнение является линейным неоднородным.
Его решение равно
сумме общего решения однородного
уравнения и частного решения неоднородного
уравнения:
Найдем частное
решение неоднородного уравнения. Для
этого перепишем уравнение (1) в следующем
виде:
(2)
Частное решение
этого уравнения будем искать в виде:
Тогда
Подставим в (2):
т.к.
выполняется для любого t ,
то должно выполняться равенство γ
= ω , следовательно,
Это комплексное
число удобно представить в виде
где А определяется
по формуле (3 ниже), а φ — по формуле (4),
следовательно, решение (2),в комплексной
форме имеет вид
Его вещественная
часть, являвшаяся решением уравнения
(1) равна:
где

(4)
Слагаемое
Хо.о. играет
существенную роль только в начальной
стадии при установлении колебаний до
тех пор, пока амплитуда вынужденных
колебаний не достигнет значения
определяемого равенством (3). В
установившемся режиме вынужденные
колебания происходят с частотой ω и
являются гармоническими. Амплитуда (3)
и фаза (4) вынужденных колебаний зависят
от частоты вынуждающей силы. При
определенной частоте вынуждающей силы
амплитуда может достигнуть очень больших
значений. Резкое возрастание амплитуды
вынужденных колебаний при приближении
частоты вынуждающей силы к собственной
частоте механической системы,
называется резонансом.
Ч
ω вынуждающей силы, при которой
наблюдается резонанс, называется
резонансной. Для того чтобы найти
значение ωрез,
необходимо найти условие максимума
амплитуды. Для этого нужно определить
условие минимума знаменателя в (3) (т.е.
исследовать (3) на экстремум).
Зависимость
амплитуды колеблющейся величины от
частоты вынуждающей силы называется резонансной
кривой.
Резонансная кривая будет тем выше, чем
меньше коэффициент затухания β и с
уменьшением β, максимум резонансных
кривых смешается вправо. Если β = 0, то
ωрез =
ω0.
При ω→0
все кривые приходят к значению
— статическое отклонение.
Параметрический
резонанс возникает в том случае, когда
периодическое изменение одного из
параметров система приводит к резкому
увеличению амплитуды колеблющейся
системы. Например, кабины, делающие
«солнышко» за счет изменения
положения центра тяжести система.(То
же в «лодочках».) См. §61 .т. 1 Савельев
И.В.
Автоколебаниями
называются такие колебания, энергия
которых периодически пополняется в
результате воздействия самой системы
за счет источника энергии, находящегося
в этой же системе.
Соседние файлы в папке Физика_1
- #
- #
- #
- #
- #
- #
21.05.2015145.41 Кб3116.doc
- #
- #
21.05.2015184.41 Кб2019.pdf
- #
21.05.201599.84 Кб122.doc
- #
21.05.2015112.13 Кб1020.doc
- #
3.1. Механические затухающие колебания
3.2. Электромагнитные затухающие колебания
3.3. Характеристики затухающих колебаний
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:
Упругая сила. , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак «минус» показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
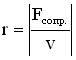
Учитывая, что и
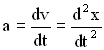
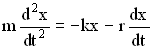
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
Обозначим , где β – коэффициент затухания,
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
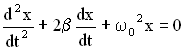
.
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний:
(физический смысл имеет только вещественный корень, поэтому
).
Период затухающих колебаний: 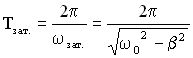
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
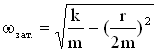
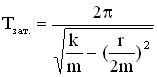
, для пружинного маятника
.
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
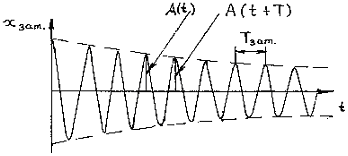
Графики зависимости смещения от времени и амплитуды от времени
представлены на Рисунках 3.1 и 3.2.
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний
Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
3.2. Электромагнитные затухающие колебания
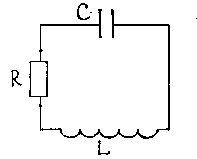
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
Рисунок 3.3.
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:
Падение напряжения:
— на активном сопротивлении: , где I – сила тока в контуре;
— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).
Подставим значения UR, UC, в уравнение, отражающее закон Кирхгофа, получим:
.
Сила тока определяется как производная от заряда , тогда
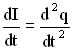
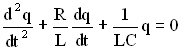
Обозначим ,
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
или
.
Амплитуда затухающих колебаний заряда имеет вид:
, где
.
Частота затухающих колебаний в LCR – контуре:

Период затухающих электромагнитных колебаний:
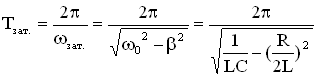
Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так
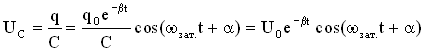
Величина 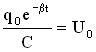
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.
Окончательное уравнение для силы тока таково:
,
где 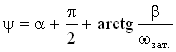
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
и энергии магнитного поля
Полная энергия в любой момент времени:
где W0 – полная энергия контура в момент времени t=0.
1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: .
Пусть за время τ амплитуда колебаний уменьшится в «e » раз («е» – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 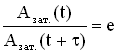
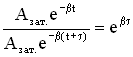
.
Промежуток времени τ, за который амплитуда уменьшается в «е» раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ — физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
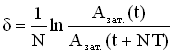
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
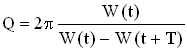
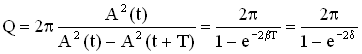
При малых значениях логарифмического декремента δ добротность колебательной системы равна
,
где Ne – число колебаний, за которое амплитуда уменьшается в «е» раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна 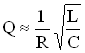
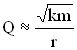
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω0 = β частота затухающих колебаний становится равной нулю ωзат. = 0, а Тзат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω0 = β запишется так: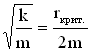
.
Для LCR – контура условие 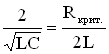
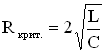
Основные формулы по физике — КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
|
Физические законы, формулы, переменные |
Формулы колебания и волны |
||||
|
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; t — время; α — начальная фаза; (ωt+α ) — фаза. |
|
||||
|
Связь между периодом и круговой частотой: |
|
||||
|
Частота: |
|
||||
|
Связь круговой частоты с частотой: |
|
||||
|
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора. |
|||||
|
Частота собственных колебаний: |
|
||||
|
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 — амплитуды составляющих колебаний, α1 и α2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания |
|
||||
|
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов. |
|
||||
|
Амплитуда затухающих колебаний: где А0 — амплитуда в начальный момент времени; β — коэффициент затухания; t — время. |
|
||||
|
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура. |
|
||||
|
Частота затухающих колебаний ω: |
|
||||
|
Период затухающих колебаний Т: |
|
||||
|
Логарифмический декремент затухания: |
|
||||
|
Связь логарифмического декремента χ и коэффициента затухания β: |
|
||||
|
Амплитуда вынужденных колебаний где ω — частота вынужденных колебаний, fо — приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: |
|
||||
|
Резонансная частота |
|
||||
|
Резонансная амплитуда |
|
||||
|
Полная энергия колебаний: |
|
||||
|
Уравнение плоской волны: где ξ — смещение точек среды с координатой х в момент времени t; k — волновое число: |
|
||||
|
Длина волны: где v скорость распространения колебаний в среде, Т — период колебаний. |
|
||||
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Коэффициент — сопротивление — среда
Cтраница 1
Коэффициент сопротивления среды в значительной степени зависит от скорости осаждения частицы.
[1]
Величина коэффициента сопротивления среды зависит от режима движения ( осаждения) частицы. В соответствии с терминологией гидравлики такое осаждение называют происходящим в ламинарном режиме.
[2]
Дина-секунда на сантиметр равна коэффициенту сопротивления среды, в которой на тело, движущееся со скоростью 1 см / с, действует сила 1 дин.
[3]
Соотношение между коэффициентом диффузии и коэффициентом сопротивления среды ( VI 1.17) было впервые получено Эйнштейном и называется формулой Эйнштейна.
[4]
С помощью In TI можно экспериментально определить коэффициент сопротивления среды п или К. Наблюдая колебательные движения точки, измеряют ряд последовательных размахов ее колебании. Если численные значения размахов составляют геометрическую прогрессию, то это значит, что силы сопротивления пропорциональны первой степени скорости.
[5]
Понятие о декременте затухающих колебаний позволяет найти коэффициент сопротивления среды экспериментально.
[6]
По формуле ( 77) рассчитывают значения коэффициента сопротивления среды при осаждении частиц.
[7]
На рис. 3 — 5 изображена графическая зависимость коэффициента сопротивления среды от режима обтекания шарообразных частиц.
[9]
Коэффициент пропорциональности а называется коэффициентом жидкого трения или коэффициентом сопротивления среды. Его значение зависит от размеров и формы движущегося тела, а также от свойств жидкости или газа.
[10]
При расчете L, необходимы опытные данные для определения коэффициента сопротивления среды с учетом инерционных членов при замедленном движении вдоль пылеосадительной камеры, а также знание распределения скоростей потока газа по объему камеры.
[11]
У обозначает момент инерции маятника относительно оси подвеса О, Р коэффициент сопротивления среды.
[12]
Обозначим жесткость пружин, соединяющих шары, через / с, коэффициент сопротивления среды движущемуся шару через г и предположим, что пружины подчиняются закону Гуна, а движущиеся шары — закону Стокса. Таким образом, константа k определяется эластическими свойствами цепных молекул полимера, а константа г характеризует внутреннее трение в полимере.
[13]
Мы можем теперь приступить к доказательству некоторых теорем, справедливых для самого общего случая, когда коэффициент сопротивления среды в различных направлениях различен и изменяется от одной точки к другой. Если распределение давлений известно, то при помощи данного в ( 28) метода мы можем построить поверхности равного давления, трубки тока, источники и стоки.
[14]
Страницы:
1
2