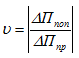Как найти коэффициент поперечной деформации - AvtoShod.ru

Лабораторная работа № 4. Определение величины коэффициента поперечной деформации для стали.

Цель работы – экспериментально определить величину коэффициента поперечной деформации (коэффициента Пуассона) для стали при испытании на растяжение.

Основные сведения

Под действием осевой нагрузки стержень изменяет свою длину и размеры поперечного сечения. Соотношение между величинами поперечной и продольной деформации для каждого материала при растяжении или сжатии является постоянной величиной и характеризует упругие свойства материала.

Абсолютную величину отношения поперечной деформации ε_поп стержня к продольной деформации ε_пр называют коэффициентом Пуассона:

Его можно вычислить, если измерить изменения линейных размеров стержня в поперечном и продольном направлениях при действии осевой нагрузки, вызывающей только упругие деформации.

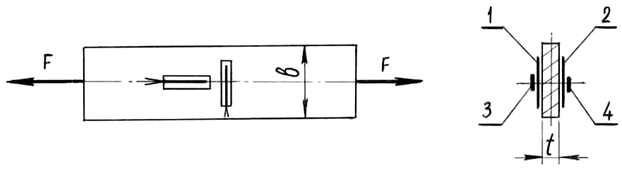
В данной работе определение коэффициента Пуассона проводится на образце, растягиваемом на испытательной машине Р-5. Образец для испытаний представляет собой широкую полосу, дающую возможность установки тензодатчиков в поперечном направлении; его длина в 4-5 раза больше ширины для исключения влияния неравномерности распределения деформаций в местах приложения нагрузки к образцу.

Наиболее быстро и наглядно коэффициент Пуассона определяется при помощи тензодатчиков сопротивления. Принцип работы датчика основан на изменении его омического сопротивления вследствие деформации проволоки датчика.

Рис. 4.1. Схема расположения рабочих тензодатчиков на образце

Рабочие датчики наклеиваются на испытуемый образец в поперечном (датчики 1,2) и в продольном (датчики 3,4) направлениях попарно на обеих сторонах растягиваемой пластины с целью исключения влияния возможного эксцентриситета продольного усилия.

Изменения сопротивления рабочих датчиков, вызванные деформацией образца, фиксируются измерительным прибором ИДЦ-1.

Порядок выполнения и обработка результатов

После установки и закрепления испытуемого образца производим его начальное нагружение небольшой нагрузкой для обжатия образца в захватах машины. Показания тензодатчиков при этой нагрузке записывают в таблицу как начало отсчета. Чем больше деформации, тем точнее можно их измерить, поэтому после предварительного обжатия нагрузку доводим до максимального значения.

При проведении опыта нужно избегать мертвых ходов приборов, для этого изменение нагрузки следует производить только в направлении, соответствующем возрастанию нагрузки. Снимаем показания тензодатчиков, также записав их значения в таблицу. После проведения опыта следует проверить начальные отчеты.

Определяем приращение показаний каждого тензодатчика, затем – средние значения приращений показаний для датчиков, установленных в продольном ΔП_пр и поперечном ΔП_поп направлениях, и экспериментальное значение коэффициента Пуассона. При испытании на растяжение продольные тензодатчики показывают увеличение отсчетов, поперечные — их уменьшение.

Так как сигналы от всех тензодатчиков идут на один и тот же регистрирующий прибор, то цена деления шкалы прибора не играет роли, и коэффициент Пуассона следует вычислять по формуле

Полученный результат необходимо сопоставить с известными значениями коэффициента Пуассона из справочника или учебной литературы и сделать заключение о достоверности проведенного эксперимента.

Контрольные вопросы

Какая величина называется коэффициентом поперечной деформации?
Как экспериментально определить коэффициент поперечной деформации (коэффициент Пуассона)?
Почему при определении продольных и поперечных деформаций используют по два тензометра?

Испытание материалов на кручение >
Другие лабораторные работы >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Стержни, работающие
на растяжение или сжатие, испытывают
помимо продольных
деформаций
и поперечные.

Как показывает
опыт, при растяжении бруска (рис.
длина его
увеличивается на величину Δl,
ширина же уменьшается на величину
Δb=b—b₁.

относительная
продольная деформация равна

Относительная
поперечная деформация равна

При сжатии бруска
продольной деформацией является
укорочение, поперечной —
удлинение.
Опыты показывают, что для большинства
материалов ε₁
в 3 — 4 раза
меньше, чем ε.

Абсолютная
величина
отношения относительной поперечной
деформации ε₁
к относительной продольной ε
называется
коэффициентом
поперечной деформации или
коэффициентом
Пуассона μ:

Коэффициент
поперечной деформации и,, так же как и
модуль упругости Е,
является
характеристикой
упругих свойств материала. Для
материалов, упругие свойства которых
одинаковы во всех направлениях, упругие
постоянные Е
и μ
полностью
характеризуют эти свойства. Такие
материалы называются изотропными.
С достаточной
для целей практики точностью к ним могут
быть отнесены сталь и другие металлы,
большинство естественных камней, бетон,
каучук, неслоистые пластмассы.

Наряду с материалами
изотропными существуют и анизотропные
материалы,
т.е. такие, свойства которых в различных
направлениях различны. К таким материалам
относятся в первую очередь дерево,
слоистые пластмассы, некоторые камни,
ткани и другие. Одно значение Е
и μ,
не может охарактеризовать их упругие
свойства, для них необходимо иметь ряд
значений упругих характеристик в
различных направлениях.

Для измерения
числовой величины μ
необходимо при растяжении или сжатии
бруска измерять одновременно продольные
и поперечные деформации. Обычно эти
измерения производятся при растяжении
образца, взятого в виде длинной и широкой
пластинки (металлы), или при сжатии
призматических образцов (камень).

Величины коэффициента
поперечной деформации для различных
материалов при деформировании их в
пределах упругости даны в таблице 1.

Зная, можно вычислить
изменение объема образца при растяжении
или сжатии. Длина образца после деформации
равна l·(1+
ε). Площадь после деформации равна F(1—
εμ)².
Объем после
деформации равен

где V
– первоначальний объем.

Так как ε
до предела
пропорциональности —
малая
величина, то квадратами ее пренебрегаем.
Тогда объем V₁
равен

Относительное
изменение объема равно

Если коэффициент
поперечной деформации μ
=0,5, то объем при деформации не меняется.
Так как для большинства материалов μ
<0,5, то растяжение сопровождается
увеличением, а сжатие —
уменьшением
объема. Для резины μ
≈ 0,5, и объем ее при растяжении почти не
меняется.

Практическое
значение появления поперечных деформаций
в связи с продольными чрезвычайно
велико. Это значение в дальнейшем будет
подробно освещено. Для иллюстрации
принятых методов и полученных формул
рассмотрим следующий пример.

К кронштейну ABC,
состоящему
из деревянного стержня АС
и железной
тяги АВ,
подвешен в
точке А груз
Q=
4 Т (рис.
9).
Сечение
тяги АВ —
круглое,
стержня квадратное. Каковы должны быть
диаметр d
стержня АВ и стороны квадрата а
(стержень
АС), если
допускаемые напряжения для дерева [σ_
]=25 кГ/см²,
дли
стали [σ₊]=900кГ/см²,
([σ_ ] —
допускаемое
напряжение на сжатие, [σ₊] —
на
растяжение); найти вертикальное и
горизонтальное перемещения точки А.
Длина АС
равна l₂ =1
м.

Усилия N₁
и N₂
в стержнях
АВ и
АС находим из условия равновесия шарнира
А, к
которому
приложена известная сила Q
и неизвестные
усилия N₁
и N₂.

Построив треугольник
равновесия для этих сил (рис. 10),
получаем

Погребные
площади сечений стержней АВ
и АС
равны

Диаметр тяги равен

сторона квадрата
равна

Обе величины
приняты с округлением —
для стального
стержня до целых мм,
для деревянного
до см.

Для определения
перемещения f
точки А
разъединим
в ней стержни и изобразим их новые длины
BA_t
и СА₂,
увеличив и уменьшив старые на Δl₁=АА₁
и Δl₂=АА₂,
не меняя пока направления стержней
(рис. 11,
а). Для
того чтобы найти новое положение точки
А, сведем
вместе деформированные стержни, вращая
их около точек В
и С.
Точки A₁
и А₂
будут
перемещаться по дугам А₁А₃
и А₂А₃,
которые по
их малости могут быть приняты за прямые,
перпендикулярные к BA±
и СА₂—
Тогда
горизонтальное перемещение точки А
будет равно

а вертикальное
(рис. 11,
б)

Отрезок

Но
A₁A₄=A₁A₅+
А₅А₄=
Δl₁·cosα+Δl₂,
так
что

Тогда

Деформации стержней
определяются формулами

Таким образом,
горизонтальное перемещение точки А
равно f₂=0,24
мм,
вертикальное

а полное перемещение
АА₃
равно

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации

Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот — длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения — поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε’ — деформации, приходящиеся на единицу длины или пощади сечения стержня.

где Δl — изменение длины стержня;

Δa — изменение площади сечения.

Продольную деформацию растяжения обычно считают положительной, деформацию сжатия — отрицательной. Продольная и поперечная деформации связаны соотношением

μ — коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.

В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.

σ = Eε

Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости — это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.

Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:

Произведение EA называется жесткостью сечения.

При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.

Источник

Коэффициент поперечной деформации

Коэффициент поперечной деформации. Кроме того, опыт работы в продольных деформациях и поперечных, работающих на стержне, растяжение или сжатие. Как показывает опыт, при растяжении штанги (рис. 11) его длина увеличивается на величину D/, а ширина уменьшается на величину D£ = £ — равную относительной продольной деформации Относительная поперечная деформация

равна ДД Сжатие стержня продольной деформации представляет собой укороченное, скрещенное растяжение. Эксперименты показывают, что для большинства материалов 3-4E в 3 раза меньше, чем.§ 9] коэффициент поперечной деформации 39

Абсолютное значение отношения относительной поперечной деформации (et)
Людмила Фирмаль

к относительной продольной деформации (e) называется коэффициентом поперечной деформации или коэффициентом Пуассона (l: Р= <2-8 ) Для свойств материала характерны коэффициент поперечной деформации C, а также модуль упругости l. Для материалов, упругие свойства которых одинаковы во всех

направлениях, упругие константы E и R. такой материал называют изотропным. С достаточной точностью на практике к ним можно отнести назначение стали и других металлов, большинства природных камней, бетона, резины, цветных пластмасс. Кроме изотропных материалов, Существуют также анизотропные материалы, то есть те, свойства которых различны в разных направлениях. К таким веществам относятся в основном клееная

древесина, пластик, камень, ткань и др. Величины E и P не могут характеризовать упругие свойства, но они должны иметь некоторые значения упругих свойств в разных направлениях. Для измерения числа Р необходимо измерить как продольную, так и поперечную деформацию при растяжении или сжатии стержня. Как правило, эти измерения производятся путем растяжения образца, взятого в виде длинной и широкой пластины (металл), или путем сжатия образца призмы (камень). В следующем примере мы рассмотрим определение коэффициента поперечной деформации. П р и М Е Р3. При волочении стального образца с узким прямоугольным поперечным сечением

со сторонами 80 мм и 3 мм продольное удлинение, измеренное на длине 100 мм, было равно 0,05 мм; такая же нагрузка прилагалась и к стальному образцу. Относительная продольная деформация равна Относительная поперечная деформация равна °b=-1 5 5.1 0-’60′ • Абсолютное образование; Это соотношение дает значение коэффициента поперечных де-40 напряжений и деформаций при растяжении и сжатии[CH и Значения поперечных деформаций при их деформировании в пределах упругости различных материалов представлены в таблице 3. Т а б л и Ц А3.

Величина коэффициента поперечной деформации. Наименование материала г Сталь…
Людмила Фирмаль

……………. М е д ы……………….. Б р о н з а…………….. Железо………………. Вести. ……………. Бюстгальтеры……………. Алюминиевый………. С и н К……………….. 0.25-0.33 0.31-0.34 0.32-0.35 0.23-0.27 0.45 0,32-0,42 0.32-0.36 0.21 Золото……………. Серебро…………. Стекло……………. Камни……………. Б е т о н………………. Резинка……………. Штекер……………. Фанера……………. Целлулоид. ……… 0.42 0.39 0.25 0.16-0.34 0.08-0.18 0.47 0.00 0.07 0.39 Зная это, можно рассчитать изменение объема образца при растяжении или сжатии. Длина образца после деформации равна Z(1—| — e). Площадь после деформации равна f(1-EP.4. Объем после деформации С=Ч(1 4-й) (1_fxs)’=в(1+е) (1-СЕ)’где V-первоначальный объем. E-это небольшое количество до предела пропорциональности, поэтому мы игнорируем этот квадрат. Тогда объем C равен V1=y[l+e (l-

2lx) J. Относительное изменение объема выглядит следующим образом П р и М Е Р4. Рассчитано относительное увеличение объема удлинительных стержней из низкоуглеродистой стали. Модуль упругости Е=2-10Е кг / см2;коэффициент поперечной деформации Р=0,3;растягивающее напряжение равно допуску низкоуглеродистой стали, т. е.=1400 кг: см*. Увеличение объема равноценно (’- 2f0=^ -. 1 1 — 2 • 0,3] = 2,8-10— = 0,028 o / o — Очень малое значение. Если коэффициент поперечной деформации|l=0,5, то объем при деформации не изменяется. Так как для большинства материалов|l<^0.5,растяжение сопровождается увеличением, сжатие — § 10] пример 41 Уменьшение объема. Резина р. 0,5, а ее объем при растяжении практически не изменяется. Практическая значимость появления поперечных деформаций, связанных с продольными очень высока. Это значение описано более подробно.

Смотрите также:

Решение задач по сопротивлению материалов

Источник

ИЗВЕСТИЯ ТОМСКОГО ОРДЕНА ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКОГО ИНСТИТУТА имени С. М. КИРОВА

Том 225 1972

КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ В ПРОЦЕССЕ ДЕФОРМИРОВАНИЯ И РАЗРУШЕНИЯ

Э. М. МИХАЙЛОВСКИЙ, к. К. ПАХОТИН, Л. М. СЕДОКОВ

‘ I

(Представлена городской научной конференцией молодых ученых и специалистов)

В пределах упругости соотношение поперечной и продольной деформаций при простом растяжении образца остается примерно постоянным и выражает одну из констарт механических свойств материала, называемую коэффициентом Пуассона — ц.

За пределами упругости коэффициент поперечной деформации существенно изменяется и может характеризоваться тремя величинами, найденными либо по упругой, либо по пластической, либо по полной (упруго-пластической) деформации.

Практическое использование в инженерных расчетах уравнения теории наибольших удлинений [1, 2],

— I1 (32 + За) < аР 0)

требует точного знания величины коэффициента поперечной деформации за пределами упругости, так как реальные хрупкие материалы перед разрушением дают остаточную деформацию, превышающую. 1—2%.

Распространение условия (1) и на область одноосного сжатия [2] приводит к тому, .что сопротивление хрупких материалов сжатию всегда равно

Ы= V. . (2)

где

ас — предел прочности на осевое сжатие,

ар—предел прочности на осевое растяжение.

Назовем соотношение пределов прочности на растяжение и на сжатие «коэффициентом хрупкости»

(3)

КГ

Из уравнения (2) и (3) следует, что коэффициент хрупкости всегда равен коэффициенту поперечной деформации ц. Однако это равенство не имеет ни теоретического, ни экспериментального обоснования. Фактическое значение этих величин приводится в табл. 1.

Из табл. 1 следует, что/ численные . значения коэффициентов [л и V для различных материалов не совпадают: для стекла .ц’ в 5 раз больше V, а для закаленной стали У7, наоборот, V в три раза больше Применительно к чугуну эти величины довольно близки, но все же расхождение превышает 10%.

Для малой упруго-пластической деформации Жуковым [7] было показано, что опытные данные хорошо совпадают с- вычисленными по формуле

3 К-Ег ,А.

‘ (4)

где Л»—модуль объемной деформации, ^ — секущий модуль. При деформациях порядка 1% расчетное значение ¡ло по зависимости (4) отличается от ^ — 0,5 не более, чем на 5%’. Учитывая, что для хрупких материалов остаточная деформация обычно превосходит 1%, можно полагать, что в момент разрушения для хрупких материалов ц всегда близок к 0,5 [8].

Таблица 1

Материал V Литература

Стекло 0,23 0,045 H. Н. Давиденков

А. Н. Ставрогин [3]

Гипс 0,22 0,140 »» >»

Чугун 0,28 0,320 Корнет и Грасси [4]

Зак. сталь Р18 0,25 0,480 3. М. Конюшко 15]

Зак. сталь У7 0,30 0,940 Ф. С. Савицкий

О. П. Бурмакина [6]

Коэффициент поперечной пластической деформации ц* Давиденков и Васильев [10] предлагают определять по уравнению

‘-¿(‘-/да ‘ <5>

где 6 — остаточная объемная деформация,

е* — относительное условное остаточное удлинение.

Мейер [10], Эндрю и Ли [11], Давиденков и Васильев установили, что при растяжении металлов до е* = 10% остаточная деформация объема находится в пределах (10-М5)ХЮ~ ‘ илда по зависимости (5) коэффициент ц* равен 0,47.

Было высказано предположение [10], что при больших деформациях ц* должен приближаться к 0,5.

Если пренебречь остаточной деформацией объема, ввиду ее очевидной малости, получим

¡х* = 1Л (6)

е* V V

График ц,* = Це*) по (6) представлен на рис. 1. Там же нанесены результаты по растяжению сплошных цилиндрических образцов из меди и латуни в состоянии поставки.

До испытания микрометром измерялись диаметры образцов на концах и в середине расчетной длины в двух взаимно перпендикулярных плоскостях. Для опытов были отобраны образцы, расхождение величин диаметров которых на расчетной длине ее превышало 0,01 мм.

Расчетная длина отмечалась двумя перпендикулярными оси образца рисками, которые наносились на делительной установке, и равнялась 20 мм. Растяжение производилось на машине ЦДМУ-30 до е* = 60 %.

^’Ыгчлцят’чгйа« |

* тгпредес микрометром

■ — микроскопа с ценой деления 0,02 мм. Полученные данные приведены

^ . ‘ * хгпроцееее-экеиеримента диаметры на расчетной длине измерялись ‘ микрометром, расстояние между рисками —с помощью специального

шйШ

?3е- С-‘ ■

0,5

с —

о^ч • ‘

1 ^^ •

0,1

ол

Рис. 1. График зависимости коэффициента пластической деформации от условной остаточной относительной ‘¿еформацииф — медь (опыт) О—латунь (опыт)

Щ’

в табл. 2. Из табл. 2 и рис. 1 следует, чтоц* значительно меньше 0,5 при деформациях, превышающих 10%.

Снижения ц* следовало ожидать, поскольку при экспериментах коэффициент пластической поперечной деформации обычно определяют как результат деления показаний приборов; регистрирующих абсолютную остаточную продольную и поперечную деформации.

— Фактический коэффициент пластической деформации, подсчитанный по соотношению истинных (логарифмических) деформаций, всегда будет равен 0,5, как показано на рис. 2 сплошной линией.*

При малых степенях деформации должна быть принята во внимание и упругая составляющая общей деформации, В этом случае коэффициент поперечной деформации

Таблица 2

Медь

Латунь

Р, кг мм и. мм Р, кг ММ /¿1 ЖИ^

0 19,91 20,45 0 20,00 20,50

3000 19,63 21,05 6000 19,63 21,29

4000 19,31 21,80 7000 19,44 21,70

5000 18,88 22,91 8000 19,18 22,35

6000 16,55 29,14 9000 18,82 23,12

10000 18,55 23,90

11000 18,20 24,90

12000 17,46 27,20

12430 16,01 32,00

асимптотически прибли-роста его значения тем

растет,

жаясь к значению 0,5, причем интенсивность выше, чем меньше упрочнение материала, и наоборот., Это вытекает из следующей формулы [9]:

= + (7)

где

Е —- модуль начальной нормальной упругости,

,2. Заказ 4746.

.17

, В — касательный модуль -г тангенс угла наклона касательной и кривой течения.- ,

. На рис. 2 зависимость (7) для меди и латуни показана пунктирными линиями.

J»

— О / О п ————

… . J»0 , h о .»и- ■ • .. • ‘/- ■

1——— 1 1 1 1 • ‘ > N

0.3

Рис. 2. 1 — график коэффициента пластической деформации, найденный по соотношению логарифмических деформаций; 2 — график коэффициента |х0 по зависимости (7) для меди: # —йедь (опыт) О—латунь (опыт) .

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Выводы

1. Коэффициент поперечной пластичеасой деформации р,*, подсчитанный как соотношение показаний тензометров, с ростом деформации-снижается и приближается к значению коэффициента Пуассона в уп-‘РУГОЙ области. ■:

— . 2- Фактический коэффициент поперечной пластической деформаций будет.равен 0,5, если.его расчет вести по соотношению истинных (логарифмических) деформаций.

3. С достаточной для инженерных расчетов точностью при определении приведенного напряжения, по теории «наибольших удлинений применительно к хрупким материала^м (с введением коэффициента хрупко-, ста) крэффициент поперечной деформации следует принимать равным 0,5, так как такое значение этого коэффициента является наиболее вероятным в момент .разрушения.

ЛИТЕРАТУРА —

1. В. А. Гастев. Краткий курс сопротивления материалов. Физматгиз, М., 1959.

2. Я: Б. Ф р и д»Й а н. Механические свойства металлов. Оборвнгиз, М., 1952. ‘ «Ъ. Н. Н. Давиденков, И. Н. Ставрогин. Изв. АН СССР, ОТН, № 8, 1954.

4. J. Cornet^and R. С. G г a s s i, J. of Appl.Méch., v. 22, № 2, 1955.

5. Ф. С. Савицкий, О. П. Бур маки на. ФММ, т. 7, вып. 3, 1959.

, 6. 3. М. К о нто» ш й о. .’Расчеты на прочность в машиностроении, сб. 46, МВТУ; Машгиз, 1955. .■:■■.■■■■■ -*1 . — >. .■■■■■<■■■.

7. А. М. Жуко е. Изв. АН СССР, ОТН, № 12, 1954. :8.- Л. М. Седок о-в. Изв. ТПИ, т. 157, Томск, 1968. , 9- Н. И. Давиденков, Д.,М. Васильев. Заводская лаборатория, т. 18; № 5, М„ 1952.

10. Mayer, Metals Technology, т. Ill, вып. 3, 1936.

11. Andrew, Lee, Jron and Steel Jnstitute 165, page 2, 1950. , ;

12. А. В. Гурьев. ФММ, т. 2, вып. 3, 1956.

Источник