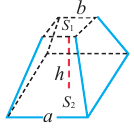
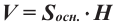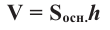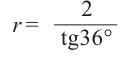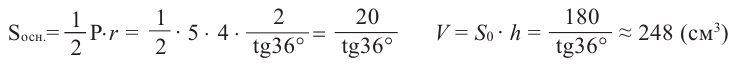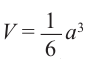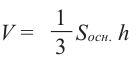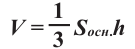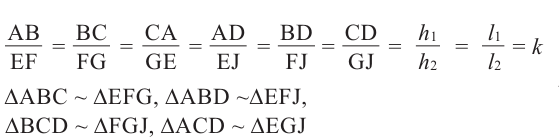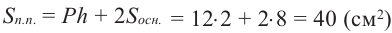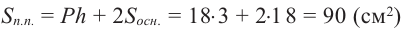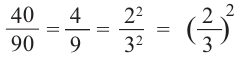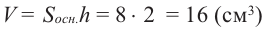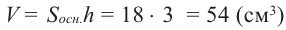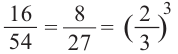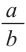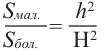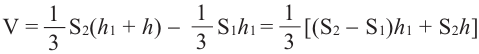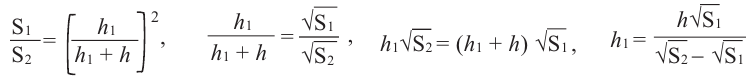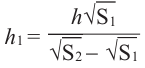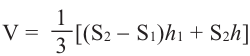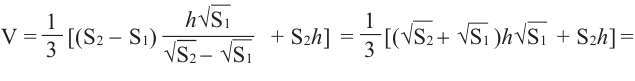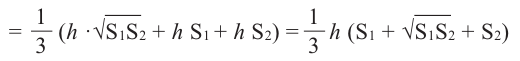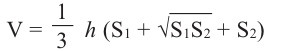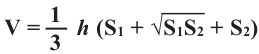Здравствуйте! Очередная порция задачек с призмами, рассматриваются треугольные призмы. Объединил несколько заданий схожих по одному «признаку» – у них через среднюю линию основания проходит сечение. Вопросы стоят о вычислении площади поверхности или объёма либо исходной призмы, либо отсечённой. Что важно здесь помнить?
Это свойство подобия фигур касающееся площади, в частности про треугольник уже речь была в одной из статей, посмотрите (п.2). Но даже, если вы вдруг забудете это, представленные задачи будут интуитивно понятны и решите вы их в одно действие.
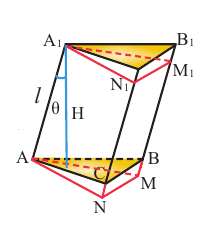
77111. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 6, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
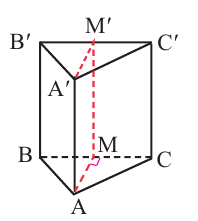
Сказано, что плоскость проходит через среднюю линию основания, то есть через точки, которые являются серединами соседних сторон треугольника. При чём она проходит параллельно боковому ребру – это означает, что указанная плоскость также проходит через середины соответствующих соседних сторон другого основания.
Без каких-либо вычислений понятно, что площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.
Посмотрите!
Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.
Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.
Ответ: 3
76147. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.
Задача обратная предыдущей. Формула для площади боковой поверхности призмы:
Значит для отсечённой призмы:
Высота у пирамид общая, поэтому площадь боковой поверхности исходной призмы зависит от периметра. Поскольку получившиеся треугольники в основании призмы подобны, и их соответствующие стороны относятся как 1:2, значит периметр основания исходной призмы вдвое больше периметра основания отсечённой.
А это означает, что и площадь боковой поверхности так же больше в 2 раза и равна 40.
Ответ: 40
27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Известно, что объём призмы равен произведению площади основания и высоты. Высота для указанных призм общая, значит изменение объёма зависит только от изменения площади поверхности.
Рассмотрим треугольники лежащие в основаниях призм – они подобны. Если рассматривать основание исходной призмы относительно основания отсечённой, то коэффициент подобия будет равен 2. Что это нам даёт?
Мы знаем, что пощади подобных фигур соотносятся как квадрат коэффициента подобия, значит:
Основание отсечённой призмы в 4 раза меньше.
Таким образом, и её объём будет в 4 раза меньше, то есть 8.
Формально можно расписать так:
Ответ: 8
74745. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7. Найдите объем исходной призмы.
Задача обратная предыдущей. Объём призмы равен произведению площади основания на высоту:
Высота общая, значит объём меняется в зависимости от изменения площади основания.
Треугольник лежащий в основании исходной призмы, как уже сказано, подобен треугольнику лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию.
Площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть:
Таким образом, площадь основания исходной призмы больше площади основания отсечённой призмы в 4 раза.
Следовательно объем исходной призмы будет в 4 раза больше объема отсечённой призмы. Таким образом, искомый объём равен 28.
Ответ: 28
Ещё три задачи про площадь поверхности призмы
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Увеличим все рёбра призмы в три раза. Что получается?
Получается, что каждая грань полученной призмы и соответствующая ей грань исходной призмы являются подобными фигурами. При чём коэффициент подобия равен 3. Мы, что площади подобных фигур пропорциональны квадрату коэффициента подобия, то есть:
Это означает, что площадь каждой отдельной грани нашей призмы увеличится в 9 раз. Так как площадь поверхности всей призмы это сумма площадей всех граней, то разумеется, что и вся площадь поверхности призмы также увеличится в 9 раз.
Ответ: 54
*На самом деле не важно о каком теле идёт речь (о призме, пирамиде, кубе, параллелепипеде), суть одна.
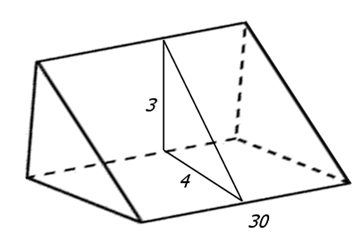
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 30 и отстоит от других боковых ребер на 3 и 4. Найдите площадь боковой поверхности этой призмы.
На момент написания статьи эта задача из открытого банка заданий ЕГЭ удалена, но мы её рассмотрим, так вернуться может туда в любой момент, а значит и быть на экзамене в будущие годы.
Для вычисления боковой поверхности призмы воспользуемся формулой:
В данном случае боковое ребро это общее ребро перпендикулярных друг другу граней, оно равно 30. Перпендикулярным сечением призмы является прямоугольный треугольник с катетами 3 и 4. По теореме Пифагора найдём его гипотенузу и сможем вычислить периметр:
Таким образом:
Второй путь решения!
Указанная выше формула для кого-то может быть не понятна. В чём её смысл и что она выражает?
Посмотрите на каждую отдельную грань (положив призму на бок) – это параллелограммы. При чём основания этих параллелограммов равны и равны они боковому ребру, то есть 30. Высоты у них будут разные.
Две нам известны 3 и 4, третья не известна. Но её мы можем найти. Разрежем призму перпендикулярно боковым рёбрам, сечением разреза будет прямоугольный треугольник с катетами 3 и 4, найдём гипотенузу:
Получается, что площадь боковой поверхности равна сумме площадей трёх параллелограммов:
Ответ: 360
72605. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота 2.
Призма правильная, значит гранями являются равные по площади прямоугольники. Так как призма шестиугольная, то имеем 6 таких прямоугольников. Площадь боковой поверхности равна сумме площадей всех боковых граней:
Ответ: 72
27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Посмотреть решение
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Посмотреть решение
27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Посмотреть решение
27150. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Посмотреть решение
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
Посмотреть решение
На этом всё, всего доброго!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна
Решение: + показать
Задача 2. В правильной четырёхугольной призме известно, что
Найдите угол между диагоналями
и
Ответ дайте в градусах.
Решение: + показать
Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
боковое ребро равно
Найдите объем призмы.
Решение: + показать
Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
высота призмы равна
Найдите площадь ее поверхности.
Решение: + показать
Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и
Площадь ее поверхности равна
. Найдите высоту призмы.
Решение: + показать
Задача 6. Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?
Решение: + показать
Задача 7. В правильной треугольной призме , все ребра которой равны
найдите угол между прямыми
и
. Ответ дайте в градусах.
Решение: + показать
Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и
и боковым ребром, равным
Решение: + показать
Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом
Одно из ребер параллелепипеда составляет с этой гранью угол в
и равно
Найдите объем параллелепипеда.
Решение: + показать
Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —
Решение: + показать
Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны
Решение: + показать
Задача 12. В правильной шестиугольной призме все ребра равны
. Найдите расстояние между точками
и
.
Решение: + показать
Задача 13. В правильной шестиугольной призме все ребра равны
Найдите угол
. Ответ дайте в градусах.
Решение: + показать
Задача 14. В правильной шестиугольной призме , все ребра которой равны
найдите угол между прямыми
и
. Ответ дайте в градусах.
Решение: + показать
Задача 15. В правильной шестиугольной призме все ребра равны
Найдите тангенс угла
Решение: + показать
Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки
см до отметки
см. Найдите объем детали. Ответ выразите в см
Решение: + показать
Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в
раза больше, чем у первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение: + показать
Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.
Решение: + показать
Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.
Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны
и наклонены к плоскости основания под углом
Решение: + показать
Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на
и
Найдите площадь боковой поверхности этой призмы.
Решение: + показать
Задача 23. В правильной треугольной призме стороны оснований равны
боковые рёбра равны
Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер
, и
и точку
Решение: + показать
Задача 24. В правильной треугольной призме стороны оснований равны
боковые рёбра равны
Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер
и
Решение: + показать
Задача 25. Объём куба равен
Построено сечение
проходящее через середины рёбер
и
и параллельное ребру
Найдите объём треугольной призмы
Решение: + показать
Задача 26. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать
Задача 27. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
площадь основания которой равна
а боковое ребро равно

Задача 28. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать
Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы
площадь основания которой равна
а боковое ребро равно
Решение: + показать

На чтение 4 мин Просмотров 66.3к. Опубликовано 13 февраля, 2019
Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Содержание
- Призма треугольная — определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Правильная призма — прямая призма, основанием которой является правильный многоугольник.
- Пример призмы
- Задачи на расчет треугольной призмы
Призма треугольная — определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
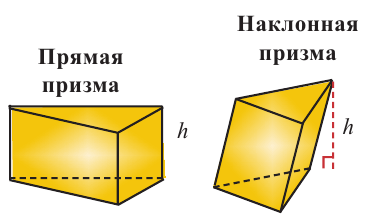
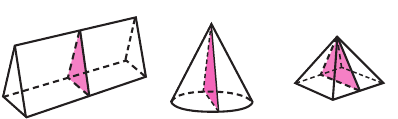
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
Sбок=Pосн.h
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Содержание:
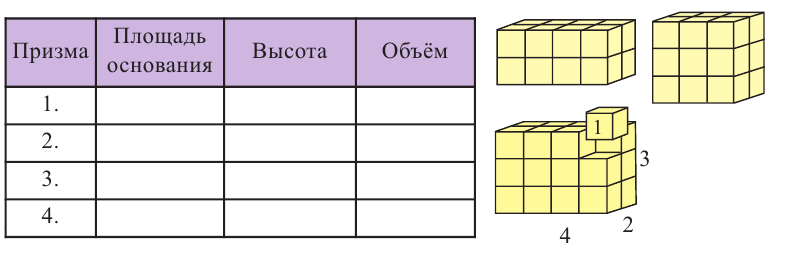
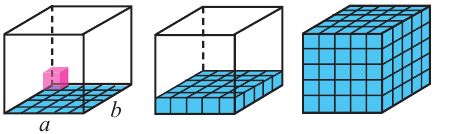
Исследование. Соберите не менее 4 призм различных размеров из кубиков и изобразите полученные призмы.
- Предположим, что ребро каждого кубика, из которых состоит призма, равна 1 единице, площадь грани равна 1 квадратной единице, а объём равен 1 кубической единице.
- Данные для каждой призмы запишите в таблицу.
- Какая связь существует между площадью основания призмы и высотой?
- Вытащите один кубик из угла конструкции и изобразите вид впереди, сверху и сбоку каждого кубоида.
Если тело можно разделить на конченое число треугольных пирамид, то оно называется простым телом. Для простых тел объём — положительная величина, численное значение которой удовлетворяет следующим свойствам.
- Объёмы конгруэнтных тел равны.
- Объём куба, ребро которого равно единице, равен кубической единице.
- Если тело можно разделить на простые части, то его объём равен сумме объёмов полученных частей.
Тела, имеющие одинаковые объёмы называются равновеликими. Объём прямоугольного параллелепипеда, размеры которого являются натуральными числами, равен
количеству кубических единиц, из которых он состоит. Можно также показать, что объём прямоугольного параллелепипеда, размеры которого заданы любыми действительными числами равен произведению трёх измерений: 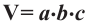
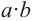
Следствие: Объём куба с ребром а равен:
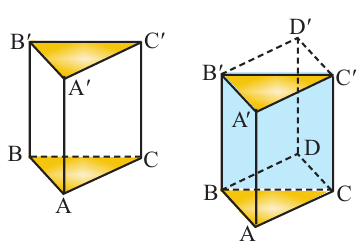
Объём любой прямой призмы равен произведению площади основания и высоты. Справедливость данного утверждения проверим на прямой призме, в основании которой лежит прямоугольный треугольник.
Достроим основание призмы до прямоугольника, получим призму, достроенную до прямоугольного параллелепипеда. Объём полученной призмы равен 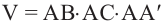
Плоскость 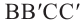
В треугольнике ABC, являющимся основанием прямой призмы, проведём высоту так, чтобы она пересекала противоположную сторону во внутренней области: 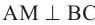
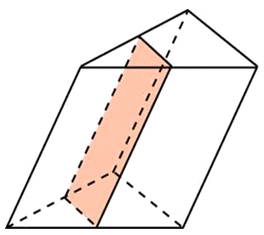
Если основанием прямой призмы является произвольный многоугольник, то её также можно разделить на треугольные призмы и найти её объём как сумму объёмов данных призм. Наклонную призму АВСА’В’С’ преобразуем в прямую призму равного объёма. Для этого:
- проведём плоскость перпендикулярную боковым рёбрам;
- отделим оставшуюся при сечении верхнюю часть призмы;
- переместим и соединим её с оставшейся внизу частью;
- высота полученной прямой призмы является боковым ребром наклонной призмы, т.е.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
Следствие. Объём наклонной призмы равен произведению перпендикулярного сечения и ребра призмы: 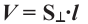
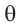
Поэтому, 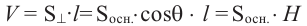
Таким образом объём призмы равен произведению площади основания и высоты.
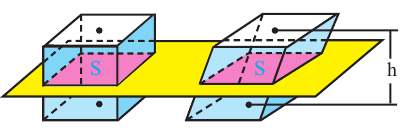
Принцип Кавальери для нахождении объёмов
Если площади сечений параллельных основаниям двух тел равны, то равны и их объёмы, при условии, что основания лежат в одной плоскости, а высоты равны. Этот принцип открыл итальянский математик Бонавентура Кавальери (1598 — 1647).
Объем призмы
Объем призмы равен произведению площади основания и высоты.
Пример №1
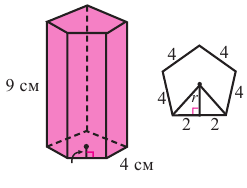
Найдём объём правильной пятиугольной призмы, стороны основания которой равны 4 см, а длина бокового ребра 9 см. Центральный угол правильного пятиугольника равен 360 : 5 = 72° значит апофема равна:
Площадь правильного многоугольника равна полупроизведению периметра и апофемы.
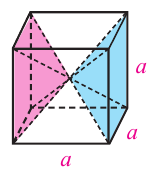
Исследование. 1. Диагонали куба деляг его на 6 конгруэнтных пирамид. Основание каждой пирамиды — грань куба, а высота
каждой пирамиды равна
а)Докажите, что объём каждой пирамиды равен
б)Докажите, что объём каждой пирамиды равен
Объём пирамиды
Объем пирамиды равен одной третьей произведения площади основанию на высоту.
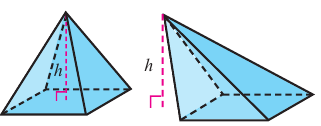
1)заданной пирамиды ТАВС;
2)пирамиды TCNM;
3)пирамиды ТМВС.
Основания 2-ой и 3-ей пирамид конгруэнтны: 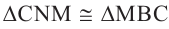
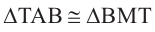
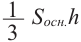
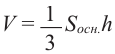
Подобие фигур в пространстве
Подобные фигуры имеют одинаковую форму и пропорциональные размеры.
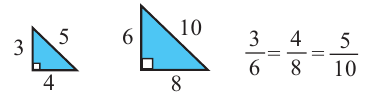
Например, прямоугольные треугольники на рисунке подобны, так как отношения соответствующих сторон равны.
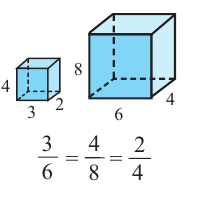
Прямоугольные параллелепипеды на рисунке подобны, так как отношения соответствующих линейных размеров равны и соответствующие грани являются подобными четырёхугольниками. Правильные многогранники подобны. В частном случае подобными являются все кубы, правильные тетраэдры и т.д.
Подобные фигуры
Если при преобразовании расстояние между любыми двумя точками, меняется в одинаковое число раз, то такое преобразование называется подобием. Одна и другая, полученная при преобразовании подобием, фигура называются подобными фигурами. Коэффициент подобия равен отношению расстояний между парой любых двух соответсвующих точек.
Пример №2
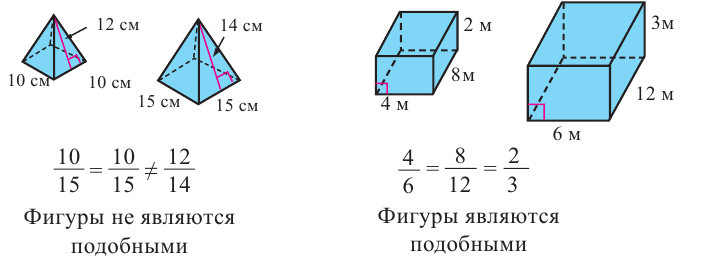
Определим подобны или нет фигуры на рисунке.
Площади поверхностей и объёмы подобных фигур
Исследование. Покажите подобны или нет следующие фигуры.
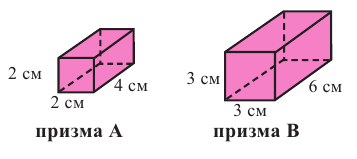
Призмы А и В (прямоугольные параллелепипеды) подобные призмы
с коэффициентом подобия равным 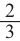
Для данных призм найдите:
а)отношение площадей полных поверхностей;
б)отношение объёмов.
а)площадь полной поверхности призмы А
площадь полной поверхности призмы В
Отношение полной поверхности призмы А к полной поверхности призмы В
б)объём призмы А
объём призмы В
Отношение объёма призмы А к объёму призмы В
Если коэффициент подобия двух пространственных фигур равен 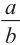
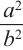
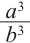
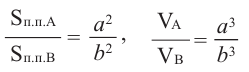
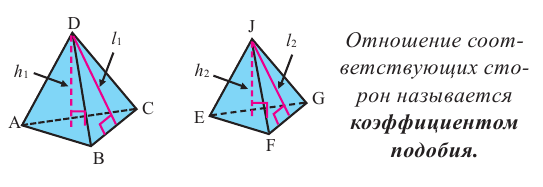
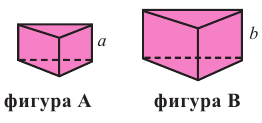
Пирамида, полученная сечением плоскости параллельной основанию, подобна данной. Коэффициент подобия можно найти из отношения соответствующих линейных размеров.
Например, на рисунке даны высоты. Тогда, отношения их боковых поверхностей, основании и полных поверхностей равно квадрату отношения высот.
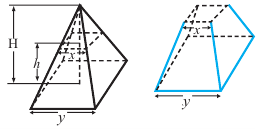
Объём усечённой пирамиды
Исследование. В древнем Египте объём правильной усечённой четырёхугольной пирамиды вычисляли по формуле 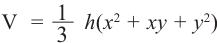
Объём усечённой пирамиды можно также найти как разность объёмов пирамид, при сечении плоскостью параллельной основанию.
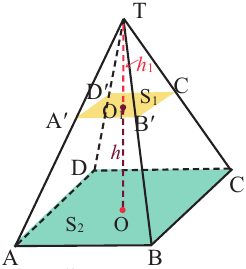
Здесь V — объём усечённой пирамиды, S2 и S1 площади нижнего и верхнего оснований. h — высота усечённой пирамиды, h1 — высота меньшей пирамиды.
Так как эти пирамиды подобны, то отношение площадей равно квадрату отношений высот. Запишем это равенство и найдём высоту меньшей пирамиды.
Учитывая выражение
в равенстве
получим:
Объём усечённой призмы
Объём усечённой пирамиды с площадями оснований 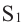
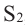
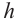
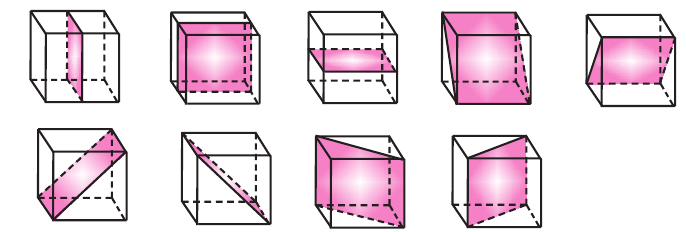
Задачи на сечение плоскостью
Пример:
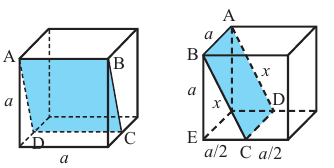
На рисунке показано сечение куба, с ребром а, плоскостью АВDО. Точки D и С являются серединами рёбер. Найдём площадь сечения.
Решение:
Дано: куб, длина ребра которого равна а точки D и С середины рёбер.
Найдите:
Для удобства повернём куб и отметим данные задачи на рисунке. Из 
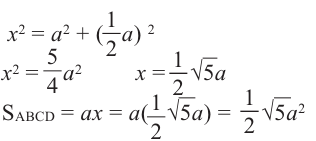
Симметрия в пространстве
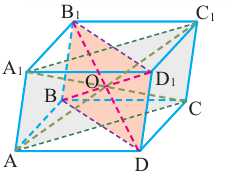
В пространственных фигурах также можно наблюдать различную симметрию. Известно, что в параллелепипеде диагональные сечения являются параллелограммами и диагонали ВD1 и DВ1 пересекаясь в точке О делятся пополам.
Можно показать, что другие диагонали также пересекаются в точке О и делятся пополам. Значит, точка пересечения диагоналей параллелепипеда является центром его симметрии.
В пространстве, помимо симметрии относительно точки и прямой, рассматривается симметрия относительно плоскости.
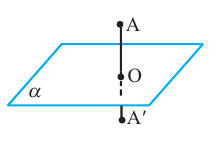
Если отрезок АА’ пересекает плоскость а посередине, и перпендикулярен плоскости, то говорят, что точки А и А’ симметричны относительно плоскости а.
Если точки фигуры, симметричные некоторой плоскости, также принадлежат этой фигуре,то эту плоскость называют плоскостью симметрии, а фигуру называют симметричной относительно плоскости.
Прямоугольный параллелепипед, у которого все линейные размеры разные, кроме центра симметрии имеет ещё три оси и три плоскости симметрии. Прямая, проходящая через точку пересечения диагоналей противоположных граней, называется осью симметрии,а плоскость, проходящая перпендикулярно через середину рёбер называется плоскостью симметрии. Параллелепипед, у которого два линейных размера равны, имеет 5 плоскостей симметрии. Данные изображения нарисуйте в тетрадь.
Точка пересечения диагоналей куба является его центром симметрии. Прямые, проходящие через середину параллельных рёбер, не принадлежащих одной грани (их всего 6) и прямые, проходящие через центры противоположных граней(их всего три), являются осями симметрии куба. У куба 9 плоскостей симметрии. Они изображены на следующих рисунках.
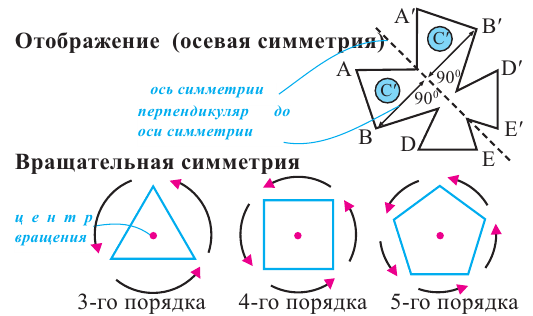
Вращательная симметрии
Вращательная симметрия пространственных фигур похожа на вращательную симметрию плоских фигур. Однако, для объёмных фигур она определяется при помощи оси вращения.
Вращательная и осевая симметрия широко применяется при изучении строения молекул веществ.
Пример №3
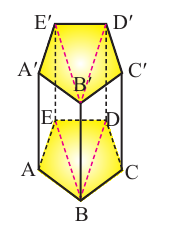
На рисунке показан вид сверху деталей, в виде правильных треугольных призм. Из них сконструирована правильная шестиугольная призма с центром основания О. Сколько деталей понадобилось для этого?
Основанием призмы является правильный шестиугольник, состоящий их 6 конгруэнтных треугольников. Каждый треугольник заполнен призмами. По изображению видно, что в один треугольник помещено 1+3 + 5 + 7 + 9 = 25 призм . Для правильной шестиугольной призмы таких призм нужно будет 6 • 25 = 150.
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
$С_1Н$ — высота
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$h$ — высота призмы.
$S_{бок}=P_{осн}·h$
$S_{п.п}=S_{бок}+2S_{осн}$
$V=S_{осн}·h$
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
2. Квадрат
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ — сторона правильного шестиугольника.
Пример:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Решение:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
$S_{п.п}=S_{бок}+2S_{осн}=P_{осн}·h+2S_{ромба}$
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
$АВ=√{5^2+12^2}=√{25+144}=√{169}=13$
$Р=13·4=52$
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
$S_{основания}={d_1·d_2}/{2}={10·24}/{2}=120$
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
$S_{п.п}=P_{осн}·h+2S_{ромба}=52·20+2·120=1040+240=1280$
Ответ: $1280$
Цилиндр — это та же призма, в основании которой лежит круг.
$S_{бок}=P_{осн}·h=2πRh$
$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$
$V=S_{осн}·h=πR^2 h$
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN {//} AC, MN = {AC}/{2}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$


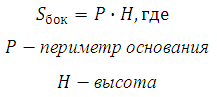
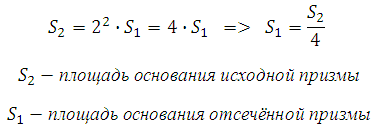
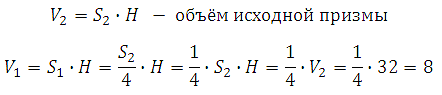
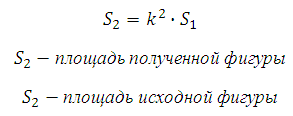
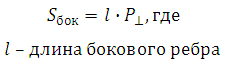















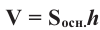
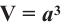
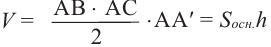
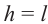 , основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.