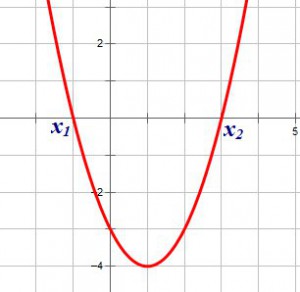
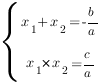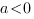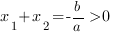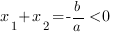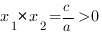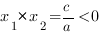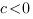Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.
— Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
— Аналогично с (a<-1), только график вытянут вниз.
— Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.
— Аналогично (a∈(-1;0)), только ветви направлены вниз.
-
Парабола пересекает ось y в точке (c).
-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) — абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)
Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример: -
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз. -
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. -
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
Как найти k и b по графику линейной функции?
Знаки коэффициентов квадратного трехчлена.
В этой статье я расскажу, как по графику квадратичной функции найти знаки коэффициентов квадратного трехчлена.
Чтобы определить знаки коэффициентов квадратного трехчлена по графику квадратичной функции 
Согласно теореме Виета, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.
Квадратное уравнение называется приведенным, если его старший коэффициент равен единице.
Чтобы уравнение 
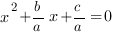
И эти же соотношения справедливы для уравнения
По графику квадратичной функции мы легко можем определить знак коэффициента 


Также по графику легко определяются знаки корней (корни квадратного трехчлена 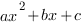

Если оба корня положительны, то 
Если оба корня отрицательны, то 
Если корень с большим модулем положителен, то 
Если корень с большим модулем отрицателен, то 
Если корни имеют одинаковые знаки, то 
Если корни имеют разные знаки, то 
Во всех случаях, определив знак коэффициента 

Рассмотрим примеры.
1. Определить знаки коэффициентов квадратного трехчлена 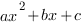

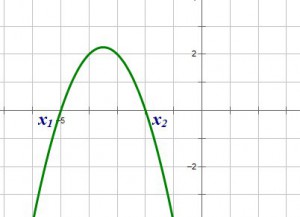
1. Ветви параболы направлены вниз, следовательно, 
2. Корни имеют одинаковые знаки, следовательно, их произведение положительно: 


3. Оба корня отрицательны, следовательно, их сумма отрицательна: 


Ответ: 


2. Определить знаки коэффициентов квадратного трехчлена 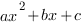

1. Ветви параболы направлены вверх, следовательно, 
2. Корни имеют разные знаки, следовательно, их произведение отрицательно: 


3. Корень с большим модулем положителен, следовательно, сумма корней положительна: 


Ответ: 


Замечание: 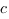

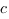
Описание презентации по отдельным слайдам:
-
1 слайд
Алгоритм
нахождения значения коэффициентов a, b, c
по графику квадратичной функции
y= ax2 +bx+c. -
2 слайд
Нахождение коэффициента a
1) по графику параболы определяем координаты вершины (m,n)
2) по графику параболы определяем координаты любой точки А (х1;у1)
3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
4) решаем полученное уравнение. -
3 слайд
Нахождение коэффициента b
1) Сначала находим значение коэффициента a
(шаг I, смотри выше)2)В формулу для абсциссы параболы m= -b/2a подставляем значения
m и a3) Вычисляем значение коэффициента b.
-
4 слайд
Нахождение коэффициента с:
1)Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с)-точка пересечения графика параболы с осью Оу.
2)Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a,b)
3)Подставляем найденные значения a, b , А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с. -
5 слайд
По графику функции найдите значения коэффициентов a, b, c
-
-
-
Нахождение коэффициентов квадратичной функции y=ax2 + bx +c
I Нахождение коэффициента а :
-
по графику параболы определяем координаты вершины (m,n)
-
по графику параболы определяем координаты любой точки A (x;y)
-
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
y=а(х-m)2+n
-
решаем полученное уравнение.
II. нахождение коэффициента b: b= — (х1 + х2) это для приведённого уравнения
-
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 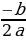
-
Вычисляем значение коэффициента b.
III. нахождение коэффициента с: с = х1 ∙ х2 это для приведённого уравнения
-
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
-
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)
-
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах2 +bх+с и находим с.
I Нахождение коэффициента а :
-
по графику параболы определяем координаты вершины (m,n)
-
по графику параболы определяем координаты любой точки A (x;y)
-
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
y=а(х-m)2+n
-
решаем полученное уравнение.
II. нахождение коэффициента b:
-
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 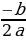
-
Вычисляем значение коэффициента b.
III. нахождение коэффициента с:
-
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
-
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)
-
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах2 +bх+с и находим с.
Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:
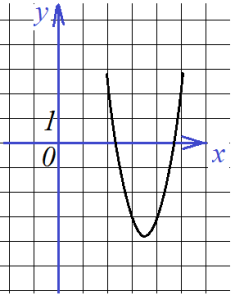
Найти все коэффициенты по графику функции
Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:
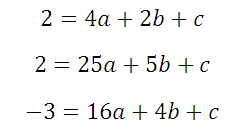
Последние два уравнения вычтем:
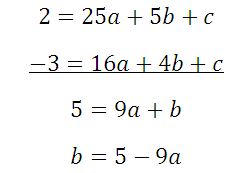
Данное выражение подставим в первое и второе уравнения:
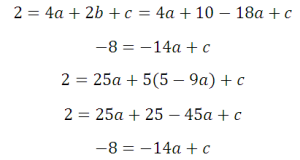
Вычтем два получившихся уравнения:
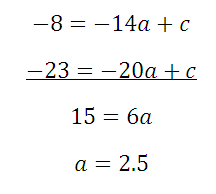
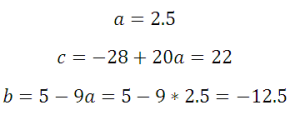
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:
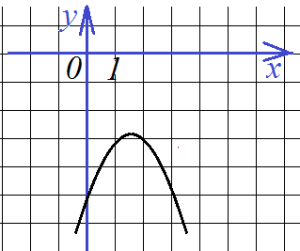
Найти все коэффициенты по графику функции
Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):
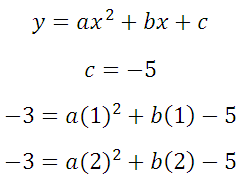
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:
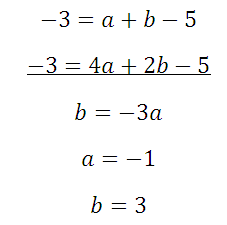
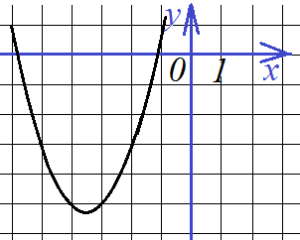
Найти все коэффициенты по графику функции
Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:
Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.
Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:
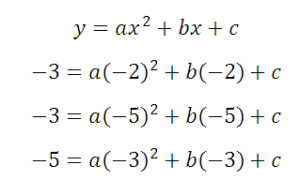
Из первого уравнения вычитаем второе:
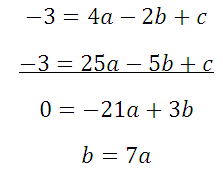
Полученное подставим в первое и третье:
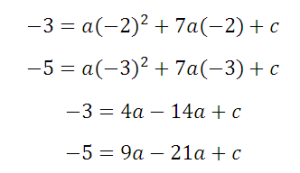
Полученные уравнения вычтем вновь, и найдем искомое:
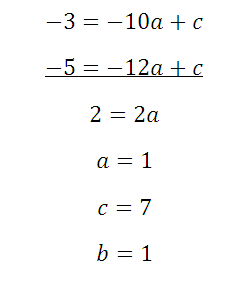
Нахождение знаков коэффициентов квадратичной функции по графику(подготовка к ГИА)
Выполнила: Давыдова Галина АнатольевнаУчитель математикиМКОУ «Кукуйская ООШ №25»Ефремовский район, тульская область
Введение
Данный материал поддерживает изучение основного курса математики и способствует лучшему усвоению базового курса . Материал можно использовать как на уроках математики, так и на дополнительных занятиях при подготовке к ГИА. Квадратичная функция является одной из главных функций школьной математики и от учащегося требуется четкое понимание и знание всех ее свойств.По знакам коэффициентов можно воспроизвести схематический график квадратичной функции, по знаку выражения (b2 – 4ac) определить существование и число корней. Ученику надо понимать, как коэффициенты квадратичной функции, их знаки, соотношения между ними определяют свойства функции влияют на расположение графика. Так же важно уметь определять знаки коэффициентов по графику квадратичной функции.
Цели :
выработать умение исследования и чтения графиков;формировать математическое мышление, необходимые человеку в современном обществе.
Задачи :
Научиться находить знаки коэффициентов по графику;овладеть рядом технических и интеллектуальных математических умений;приобрести определенную математическую культуру;
Квадратичная функция
Квадратичной функцией называется функция вида: y=aх2+bx+c,где а – коэффициент при старшей степени неизвестной х (первый коэффициент), b – коэффициент при неизвестной х (второй коэффициент), с — свободный член.
Для определения знака коэффициентов квадратичной функции по графику воспользуемся теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.
Квадратное уравнение называется приведенным, если его старший коэффициент равен единице.Чтобы уравнение aх2+bx+c =0 стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение х2+b/ax+c/a =0 . Для него справедливы соотношения: х1 + х2 = — b / а х1 • х2 = с/аИ эти же соотношения справедливы для уравнения aх2+bx+c=0
Определение знака коэффициента а по графику квадратичной функции
1. если ветви параболы направлены вверх, то а>0 , 2. если ветви параболы направлены вниз, то а<0 .
Определение знака корней квадратного трехчлена по графику квадратичной функции
Корни квадратного трехчлена aх2+bx+c – это абсциссы точек пересечения графика функции y=aх2+bx+c с осью абсцисс Если оба корня положительны, то х1 + х2 = -b / а >0Если оба корня отрицательны, то х1 + х2 = — b / а <0Если корень с большим модулем положителен, то х1 + х2 = — b / а >0.Если корень с большим модулем отрицателен, то х1 + х2 = — b / а <0.Если корни имеют одинаковые знаки, то х1 • х2 = с/а >0Если корни имеют разные знаки, то х1 • х2 = с/а<0.Во всех случаях, определив знак коэффициента а по направлению ветвей параболы, мы легко найдем знаки коэффициентов b и c
Пример №1
Определить знаки коэффициентов квадратичной функции , если график функции имеет вид:1. Ветви параболы направлены вниз, следовательно, а<0.2. Корни имеют одинаковые знаки, следовательно, их произведение положительно: х1 • х2 = с/а >0. Так как а<0 , следовательно, с <0 .3. Оба корня отрицательны, следовательно, их сумма отрицательна: х1 + х2 = — b / а <0. Так как а <0 , следовательно, b<0.Ответ: а<0 , b<0, с <0.
Пример №2
Определить знаки коэффициентов квадратичной функции , если график функции имеет вид:1. Ветви параболы направлены вверх, следовательно, а>0.2. Корни имеют разные знаки, следовательно, их произведение отрицательно: х1 • х2 = с/а<0. Так как а>0 , следовательно, с<0.3. Корень с большим модулем положителен, следовательно, сумма корней положительна: х1 + х2 = — b / а >0. Так как а>0 , следовательно, b<0.Ответ: а>0. b<0, с<0 .
Модуль «Алгебра» прототип задания 5
График какой из приведенных ниже функций изображен на рисунке?1. У= -х2 -6х-52. У= х2 +6х+53. У= х2 -6х+54. У= -х2 +6х-5 Решение:Ветви направлены вверх, следовательно а>0.Сумма корней отрицательна, х1 + х2 = -6, а=1>0,следовательно, b >0, b=6 Ответ: 2
Найдите знаки коэффициентов а;b и с по графику функции, изображенному на рисунке.
Литература
1. «Алгебра. Учебник для 8 кл. общеобразовательных учреждений» Ю.Н. Макарычев и др., изд-во «Просвещение», 2010.;2. «Алгебра. Учебник для 9 кл. общеобразовательных учреждений» Ю.Н. Макарычев и др., изд-во «Просвещение», 2011.;3. ГИА, Математика, 3000 задач с ответами, Часть 1, Семенов А.Л., Ященко И.В., 2013.