Коэффициент корреляции вводится как
величина, которая служит мерой тесноты
(силы) линейной корреляционной зависимости
признаков.
Рассмотрим сначала эксперименты, в
которых одновременно измеряются только
две величины (обозначим их Y
иX ). Пусть
проведеноn независимых
совместных измерений признаковY
иX , в результате
которых полученоnпар чисел:
(x1,
y1),
(x2,
y2),
(x3,
y3),
…, (xi
, yi
), …, (xn,
yn).
(4.7)
Такую совокупность пар чисел можно
рассматривать как случайную выборку
из генеральной совокупности всех
возможных значений пары (Y
,X). Поэтому получаемое
по этим данным значение коэффициента
корреляции называют выборочным.
Выборочный коэффициент корреляции
определяется равенством

где yi
— экспериментальное значение
величиныY ,
соответствующееxi
;
n – объем
выборки;
— выборочные средние признаковX
иY ;
—выборочныесредние квадратичные
отклонения признаковX
иY .
Если вместо выборочных использовать
исправленныесредние квадратичные
отклоненияsx,sy
, то вычисление выборочного
коэффициента корреляции производится
по формуле
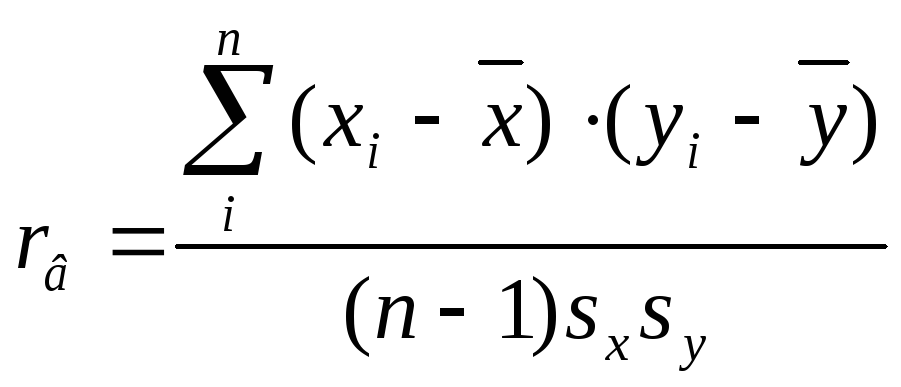
(4.9)
Почему введенное таким образом выражение
для rв способно служить мерой тесноты
корреляционной связи? Дело в том, что
выражение дляrв
является суммой произведений так
называемых нормированных отклонений.
Нормированное отклонениеt(xi)
вариантыxiесть разность между значениемxiварианты и ее средним значением,
отнесенная к среднему квадратичному
отклонению этой варианты:.
Аналогичноесть нормированное отклонение
вариантыyi
. Используя нормированные отклонения,
выражение дляrвможно представить в видеrв=.
При коррелированности (т.е. наличии
сопряженности изменения) признаковX
иY величиныt(xi)
иt(yi)
принимают положительные и отрицательные
значения некоторым регулярным образом,
поэтому произведенияt(xi)
t(yi)
входят вбольшей
частью с одинаковым знаком, что
обеспечивает отличиеrв
от нуля. Кроме того, при
коррелированности признаковX
иY и модули
величинt(xi)
иt(yi)
меняются согласованно: например, в
случае линейной корреляции большим по
модулю значениямt(xi)
соответствуют, как правило, большие по
модулю значения t(yi),
что также приводит к отличиюrв
от нуля. Наоборот, при отсутствии
корреляции знаки величинt(xi)
иt(yi)
будут меняться чисто случайным образом,
из-за чего число положительных слагаемых
в суммебудет примерно равно числу отрицательных,
что приведет к их взаимному сокращению
и равенствуrв =
0.
Существует много различных рабочих
формул для вычисления rв
прямым способом, т.е. при
непосредственном использовании
полученных в результате измерений
значенийxi
иyi
. Здесь приведены лишь наиболее
употребимые из них. Выражение
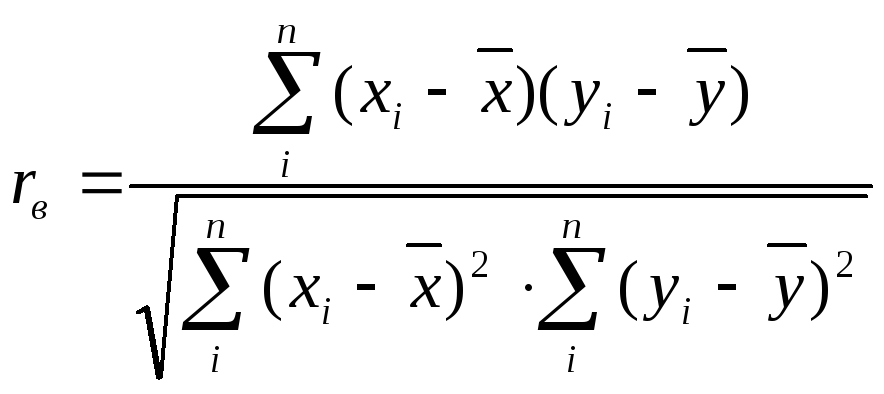
получается из (4.8) заменой
и
выражениями


выражении используются только отклонения
вариант от средних.
Еще одна формула для вычисления rвполучается в результате преобразования
числителя в выражении (4.9):
Отсюда получаем
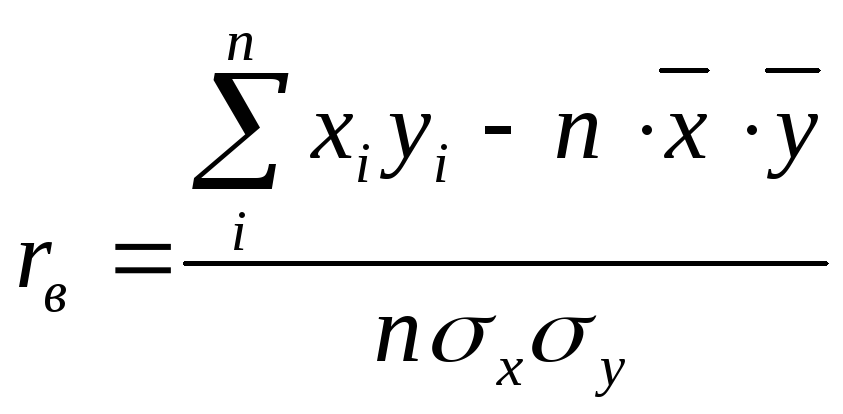
или
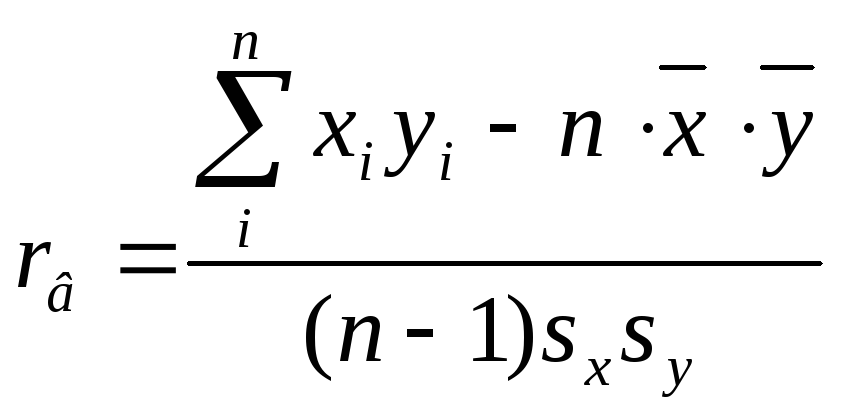
Формулы (4.8 ), (4.9) и (4.10 ) для вычисления
выборочного коэффициента корреляции
применимы и в случаях, когда данные
измерений не могут быть сгруппированы,
из-за того, что различные значения xi
иyi
величинX иY
наблюдаются по одному разу, и в тех
случаях, когда данные могли бы быть
сгруппированы, но решено группировку
не делать.
Если данные n
экспериментов по совместному измерению
значений величинY
иX сгруппированы
и представлены в виде корреляционной
таблицы (типа приведенной в 4.4.2.), то
выборочный коэффициент корреляции
удобно вычислять по формуле
, (4.13)
где x,y
– варианты (наблюдавшиеся значения)
признаковX иY
;
nxy
— частота (число появлений)
наблюдавшейся пары вариант (x
,y );
n – объем
выборки ();
— выборочные средние признаковX
иY ;
— выборочные средние квадратичные
отклонения признаковX
иY .
Если использовать исправленныесредние квадратичные отклоненияsx,sy
, то
.
(4.14)
Важно отметить, что выборочный коэффициент
корреляции rв и угловой коэффициентk
прямой линии регрессии (4.4) связаны
между собой соотношением
(4.15)
или
.
(4.16)
Это выражение не только дает еще один
способ вычисления коэффициента
корреляции, но и явно указывает на то,
что rв является мерой именно линейной
корреляционной связи.
Пример 4.3. Проверить прямым вычислением
справедливость формулы (4.15) по данным
примера 4.2.
Решение. По данным примера 4.2.
Выборочные дисперсии равны
,
.
Выборочные средние квадратичные
отклонения равны
Отсюда
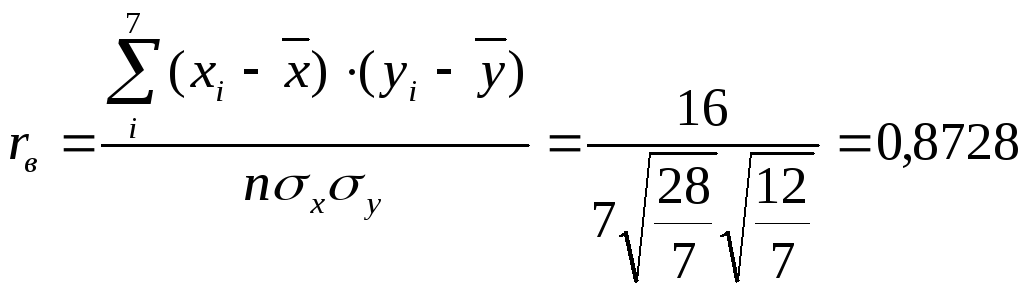
С другой стороны
Если вместо выборочных использовать
исправленные средние квадратичные
отклонения, которые оказываются в данном
случае равными sx
=,sy
=
,
то
Е
Какие значения rв
можно считать большими, а какие
средними или малыми? Оказывается, что
при наличии корреляции степень влияния
изменений одного признака на изменения
другого может быть выражена квадратом
коэффициента корреляции.
Это значит, что приrв
= 0,9 81% вариации одного признака
обусловлен вариацией другого признака,
в остальных же 19% случаев совпадение
или несовпадение вариаций признаков
по знаку и величине является чисто
случайным. Приrв
= 0,3 такая обусловленность имеет
место менее, чем для 10% вариаций. Таким
образом, корреляцию (связь) принято
считать: очень тесной, если;
тесной, если;
средней (значительной), если;
умеренной, если;
слабой, если
Изучаемые признаки X
иYчасто имеют
различную размерность, но коэффициент
корреляцииrвесть всегда величинабезразмерная.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейный коэффициент корреляции
Краткая теория
Под теснотой связи между
двумя величинами понимают степень сопряженности между ними, которая
обнаруживается с изменением изучаемых величин. Если каждому заданному
значению
соответствуют
близкие друг другу значения
, то связь считается тесной (сильной); если
же значения
сильно
разбросаны, то связь считается менее тесной.
Рассмотрим наиболее важный
для практики и теории случай линейной зависимости вида:
При тесной корреляционной
связи корреляционное поле представляет собой более или менее сжатый эллипс. Две
корреляционные зависимости переменной
от
приведены на рисунке.
Очевидно, что в случае (а)
зависимость между переменными менее тесная, чем в случае (б), так как точки
корреляционного поля (а) дальше отстоят от линии регрессии, чем точки поля (б).
Перейдем к оценке тесноты
линейной корреляционной зависимости. Для показателя тесноты связи нужная такая
стандартная система единиц измерения, в которой данные по различным
характеристикам оказались бы сравнимы между собой. Статистика знает такую
систему единиц. Эта система использует в качестве единицы измерения переменной
ее среднее квадратическое отклонение
.
Учтем, что
и запишем
уравнение парной линейной зависимости
в эквивалентном виде:
В этой системе величина:
показывает, на сколько
величин
изменится
в среднем
, когда
увеличится
на одно
.
Величина
является
показателем тесноты связи и называется линейным коэффициентом корреляции. Коэффициент
корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции.
Если
, то корреляционная связь между переменными
называется прямой, если
– обратной.
Приведем другие модификации
формулы для расчета линейного коэффициента корреляции:
или
Наиболее часто для расчета
используют формулу, получаемую простыми преобразованиями:
По этой формуле
находится
непосредственно из данных наблюдений и на значении
не
скажутся округления данных, связанных с расчетом средних и дисперсий.
Линейный выборочный
коэффициент корреляции
(при
достаточно большом объеме выборки
) обладает следующими свойствами:
-
Коэффициент корреляции
принимает значения на отрезке
, т.е.
. При этом, чем ближе по модулю
к
единице – тем теснее связь.
При
корреляционная
связь представляет собой линейную функциональную зависимость. При этом все
наблюдаемые значения располагаются на прямой линии.
При
линейная
корреляционная связь отсутствует. При этом линия регрессии параллельна оси
.
Расчет линейного коэффициента корреляции предполагает, что
переменные
и
распределены нормально. В других случаях
(когда распределения
и
отклоняются от нормальных) линейный
коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи
переменных.
Пример решения задачи
Задача
Компания,
занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон
определенной модели цену, дифференцированную по регионам. Следующие данные
показывают цены на видеомагнитофон в 10 различных регионах о соответствующее им
число продаж:
|
Число продаж, шт. |
420 | 380 | 350 | 400 | 440 | 380 | 450 | 425 | 430 | 480 |
| Цена, тыс.руб. | 5.6 | 6.0 | 6.5 | 6.0 | 5.0 | 6.4 | 4.5 | 5.0 | 5.7 | 4.4 |
Рассчитайте
выборочный коэффициент линейной корреляции и проверьте его значимость
при
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим
расчетную таблицу:
Вычислим
линейный коэффициент корреляции:
Вывод
Связь
между числом продаж и ценой очень тесная, обратная – с уменьшением цены
увеличивается объем продаж.
Проверим
значимость коэффициента корреляции:
По таблице критических точек t-критерия Стьюдента (по уровню значимости
и числу степеней свободы
) находим:
— коэффициент корреляции значим.
Кроме этой задачи на другой странице сайта есть еще
задача на расчет коэффициента корреляции, коэффициента детерминации, построение линии линейной регрессии и корреляционного поля.
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 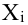
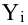
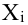
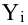
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: 
Коэффициент r мы считаем в Excel, с помощью функции 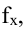
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:
Связь нельзя считать случайной, если:
В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 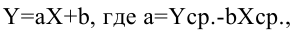
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 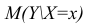
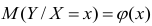
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
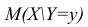
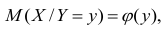
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек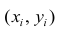
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
Аналогично определяется кривая регрессии X по Y (X на Y):
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее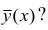
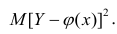
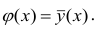
Если рассеивание вычисляется относительно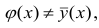
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
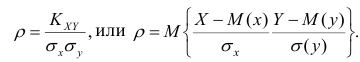
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 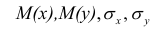
математического ожидания является среднее арифметическое, т.е.
Оценкой дисперсии служит выборочная дисперсия, т.е.
Тогда выборочный коэффициент корреляции
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
функция регрессии X на Y — следующий вид:
Выражения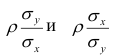
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 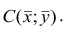
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
Возведём выражение под знаком суммы в квадрат:
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что
Таким образом, окончательно получаем
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 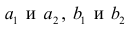
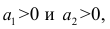
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 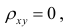
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
где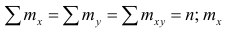
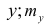
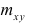
Из формулы (1.2) очевидно, что 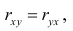
Поле корреляции. Вычисление оценок параметров двумерной модели
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 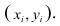
Пару случайных чисел 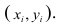
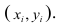
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 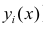
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 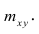
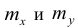
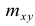
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
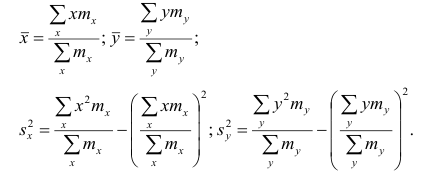
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 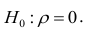
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 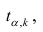
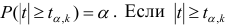
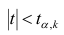
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
В этом, случае доверительный интервал для римеетвид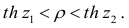
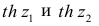
где 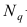
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
где 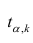
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 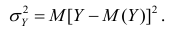
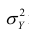
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 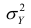
Первое слагаемое обозначим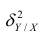
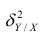
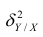
Покажем, что 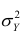
Для простоты полагаем распределение дискретным. Имеем
так как при любом х справедливо равенство
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 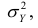
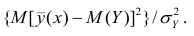
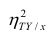
Разделив обе части равенства (1.9) на 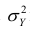
Из последней формулы имеем
Поскольку 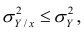
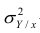
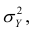
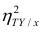
Все сделанные выводы справедливы и для 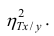
следует, что 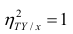
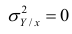
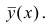
Далее, из равенства (1.12) следует, что 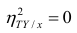
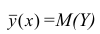
Аналогичными свойствами обладает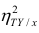
Часто используют величину
Считают, что она не может быть отрицательной. Значения величины 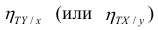
Значения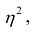
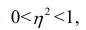
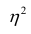
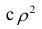
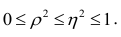
Разность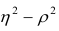
При вычислении 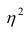
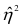
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 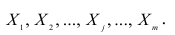
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 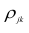
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
где 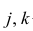
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между 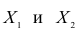
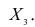
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 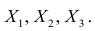
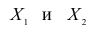
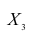
корреляции и имеет вид
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при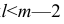
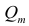
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
Для определения частного коэффициента корреляции второго порядка, например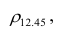
вычеркнув из исходной матрицы 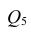
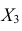
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
где 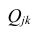
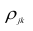
матрицы 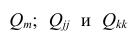
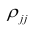
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
Формула выборочного частного коэффициента корреляции имеет вид
где 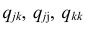
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 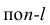
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции
где 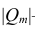
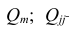
дополнение к элементу
Квадрат коэффициента множественной корреляции 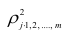
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 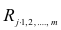
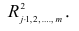
где 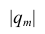
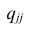
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
Пусть 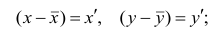
что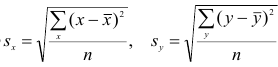
В зависимости от того, что принять за меру различия между величинами 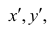
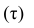
Введём следующую меру различия между объектами: будем считать 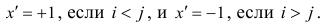
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как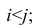
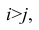
Рассмотрим формулу ( 1 .22). В нашем случае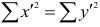
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.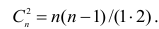
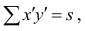
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 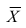
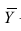
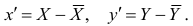
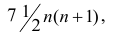
Тогда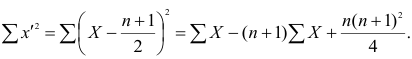
чисел натурального ряда равна
Тогда
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину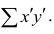
Коэффициент корреляции рангов Спирмэна
У коэффициентов 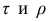
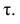
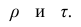
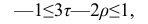
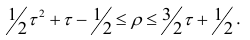
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму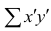
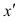
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 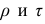
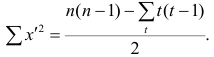
где t и u—число связанных пар в последовательностях.
Обозначая 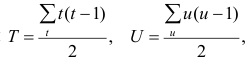
Аналогично находим выражение для р. Только в этом случае
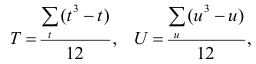
последовательностях, а
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации
где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
Пример:
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне
Решение. Для вычислений составим таблицу. Находим суммы
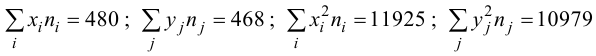
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
Проверим значимость 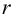
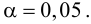
По таблице распределения П6 Стьюдента 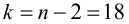
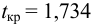
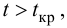
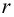
Пример:
Для данных табл. 13 найти корреляционное отношение
Для вычисления эмпирического корреляционного отношения найдем групповые средние
Тогда
Вычисляем корреляционное отношение
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. The correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where
The formula for 
the formula for 
where
The formula for 
the formula for 
Pearson’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where
Alternative formulae for 

where
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) More general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, 
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is
This uncentered correlation coefficient is identical with the cosine similarity.
The above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is
-
(3)
where in (3)
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is[citation needed]
radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance, 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
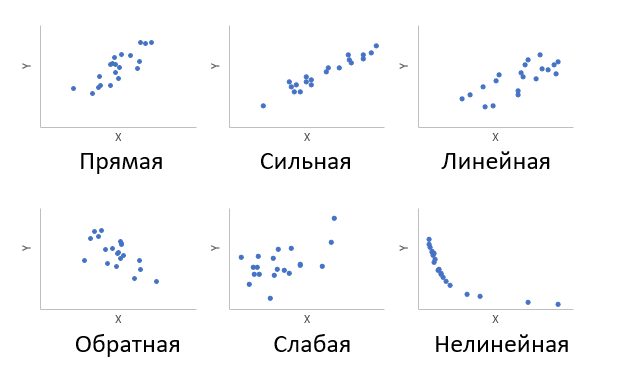
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
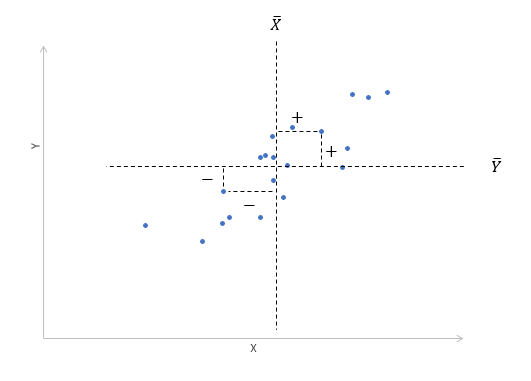
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
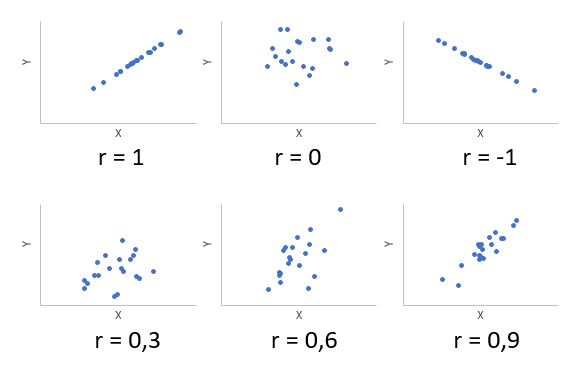
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
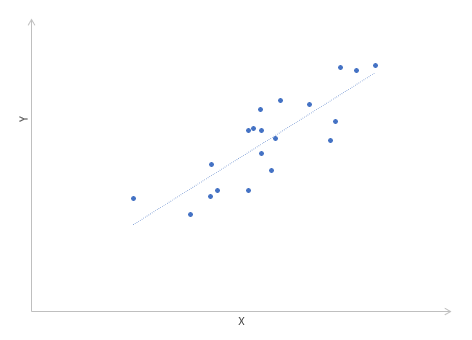
Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
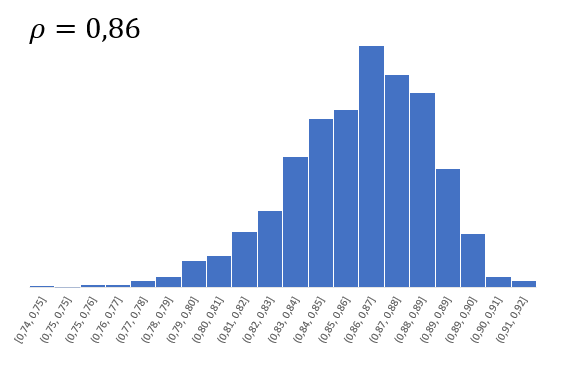
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
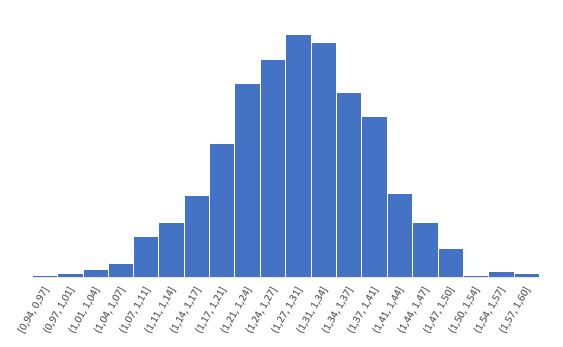
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
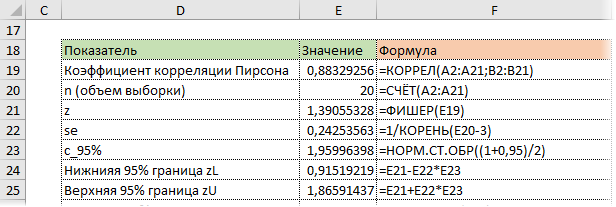
Нижняя граница z:
Верхняя граница z:
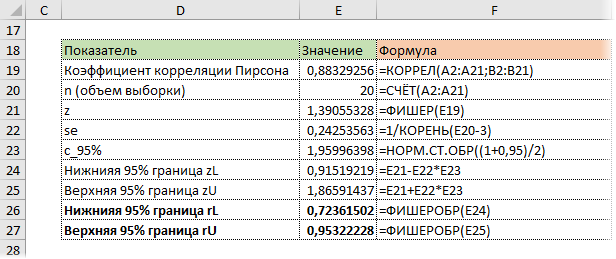
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Верхняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
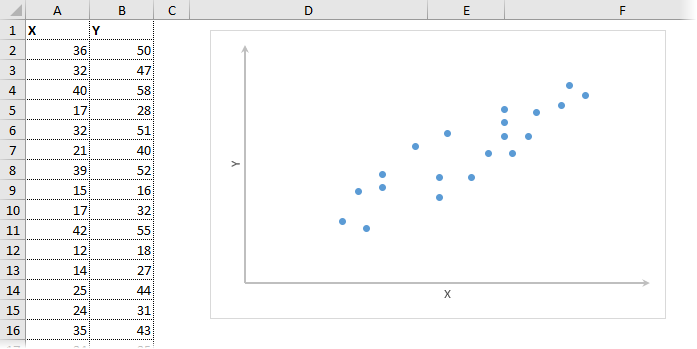
Корреляционный анализ в Excel лучше начинать с визуализации.
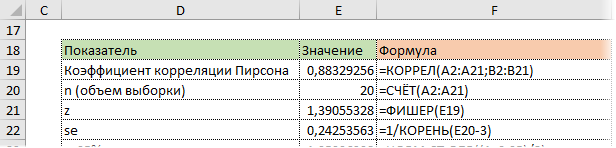
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
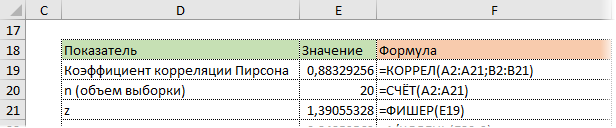
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
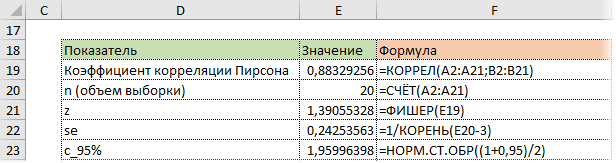
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
↓ Скачать файл с примером ↓
Поделиться в социальных сетях:


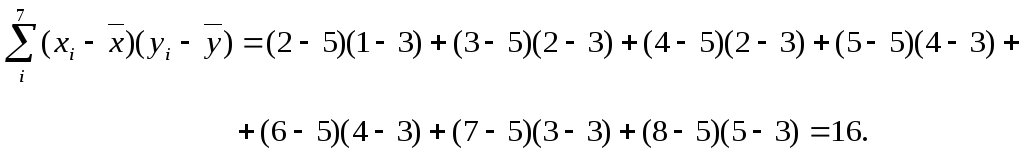
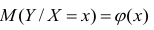
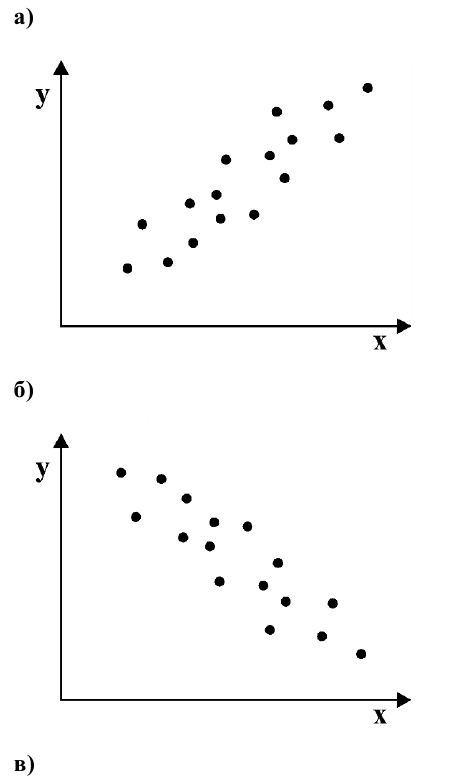
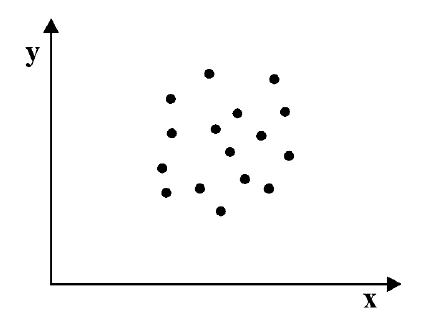
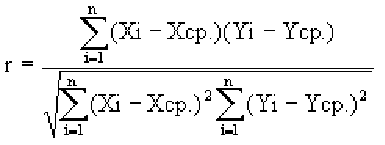
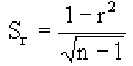
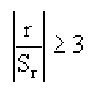
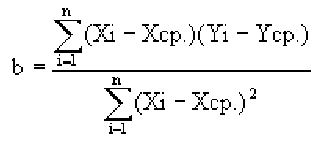
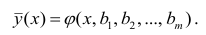
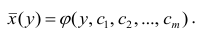
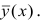
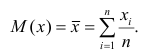
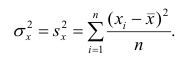
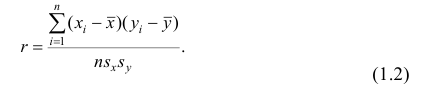
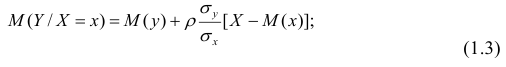
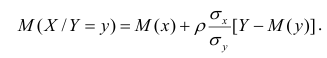
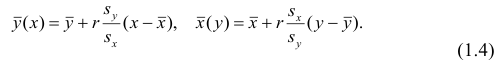
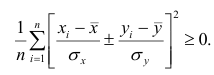
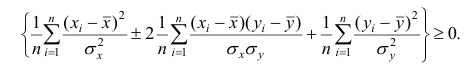
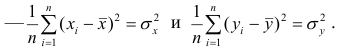
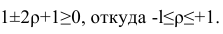
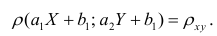
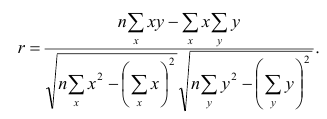
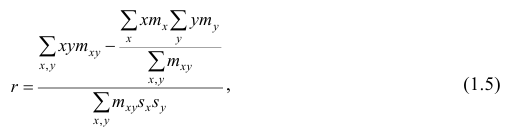
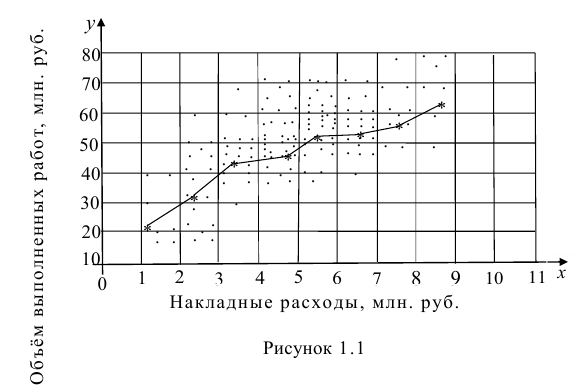
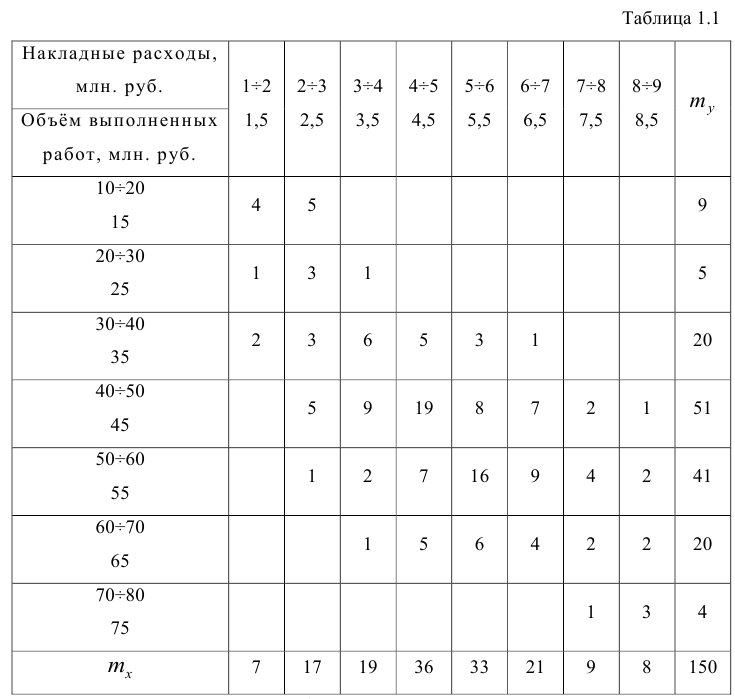
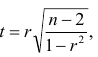
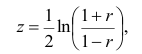
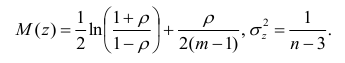
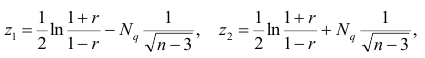
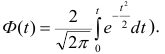
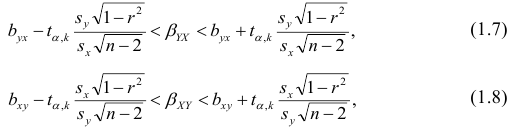
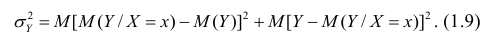
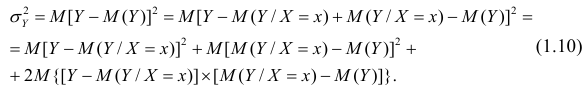
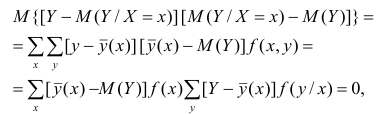
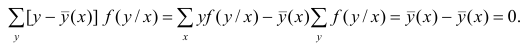
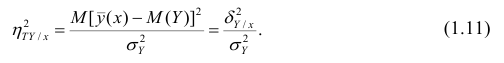
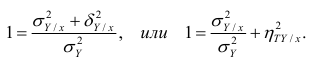

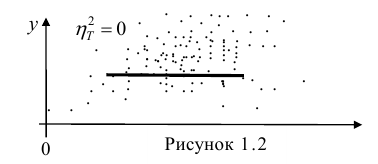
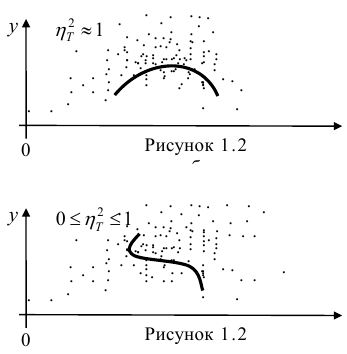

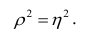
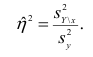

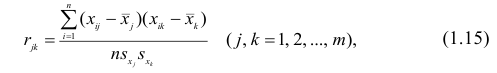
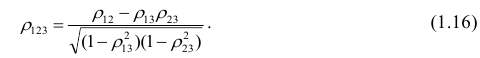
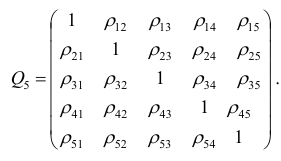
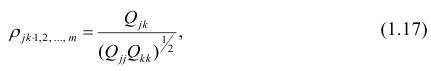
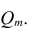
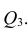
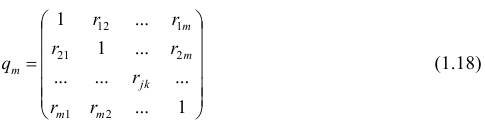


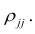

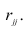
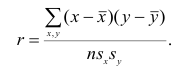

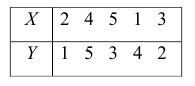
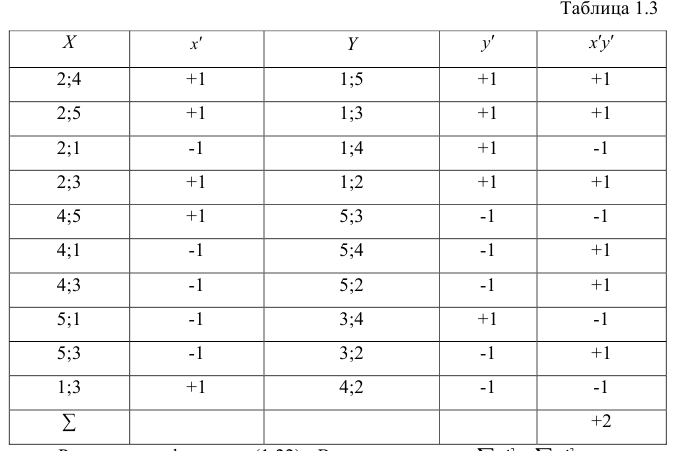
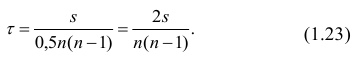
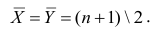
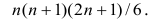
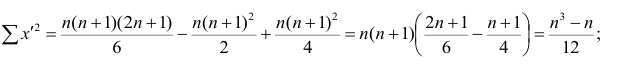
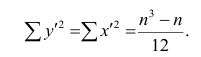
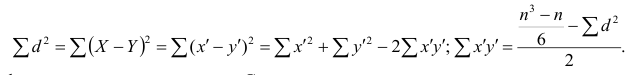

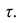
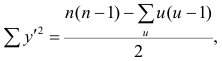
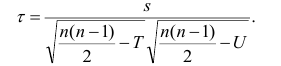
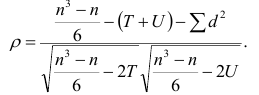

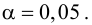
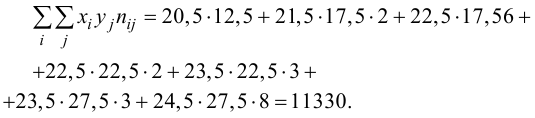
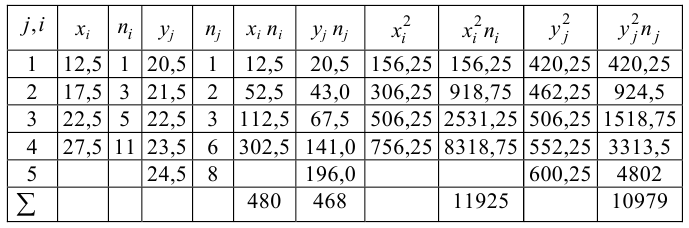
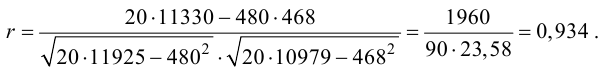
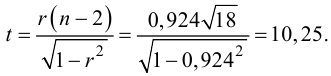
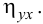
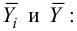
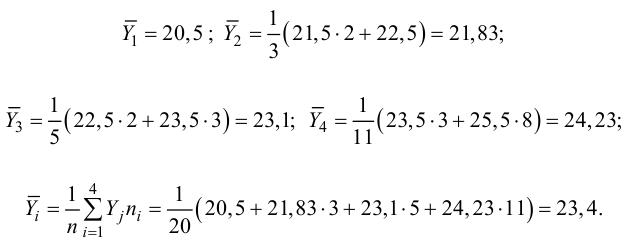
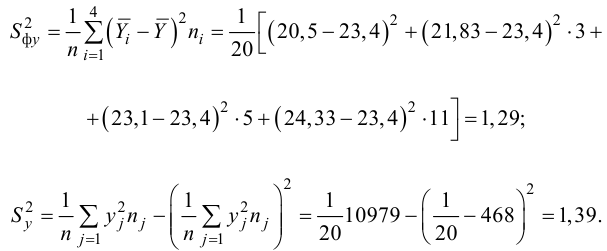
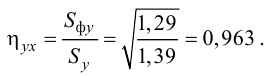



![{displaystyle operatorname {cov} (X,Y)=operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e88bc4ba085b98d5cca09b958ad378d50127308)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})]}{sigma _{X}sigma _{Y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042c646e848d2dc6e15d7b5c7a5b891941b2eab6)
![{displaystyle {begin{aligned}mu _{X}={}&operatorname {mathbb {E} } [,X,]\mu _{Y}={}&operatorname {mathbb {E} } [,Y,]\sigma _{X}^{2}={}&operatorname {mathbb {E} } left[,left(X-operatorname {mathbb {E} } [X]right)^{2},right]=operatorname {mathbb {E} } left[,X^{2},right]-left(operatorname {mathbb {E} } [,X,]right)^{2}\sigma _{Y}^{2}={}&operatorname {mathbb {E} } left[,left(Y-operatorname {mathbb {E} } [Y]right)^{2},right]=operatorname {mathbb {E} } left[,Y^{2},right]-left(,operatorname {mathbb {E} } [,Y,]right)^{2}\&operatorname {mathbb {E} } [,left(X-mu _{X}right)left(Y-mu _{Y}right),]=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [,X,]right)left(Y-operatorname {mathbb {E} } [,Y,]right),]=operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,],,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2469cdb397ef7d50c200b03c9e9f7311f0ab2b1)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,]}{{sqrt {operatorname {mathbb {E} } left[,X^{2},right]-left(operatorname {mathbb {E} } [,X,]right)^{2}}}~{sqrt {operatorname {mathbb {E} } left[,Y^{2},right]-left(operatorname {mathbb {E} } [,Y,]right)^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5984dfb290912b0e0b92a984bf49cdd628c38b2c)








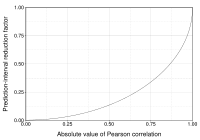

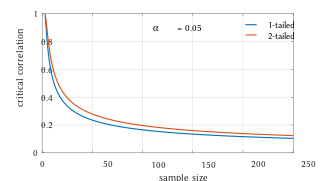








![z={frac {x-{text{mean}}}{text{SE}}}=[F(r)-F(rho _{0})]{sqrt {n-3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7a3d54a70f9005e3bf9a2accf62cbf0fa0ea71)
![{displaystyle 100(1-alpha )%{text{CI}}:operatorname {artanh} (rho )in [operatorname {artanh} (r)pm z_{alpha /2}{text{SE}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc3f0ee39499c97bb851229113f49d83100bf2)
![{displaystyle 100(1-alpha )%{text{CI}}:rho in [tanh(operatorname {artanh} (r)-z_{alpha /2}{text{SE}}),tanh(operatorname {artanh} (r)+z_{alpha /2}{text{SE}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf658969d39ea848505750b5cd76db21da78dd5c)


![{displaystyle {begin{aligned}r(Y,{hat {Y}})&={frac {sum _{i}(Y_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}(Y_{i}-{hat {Y}}_{i}+{hat {Y}}_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}[(Y_{i}-{hat {Y}}_{i})({hat {Y}}_{i}-{bar {Y}})+({hat {Y}}_{i}-{bar {Y}})^{2}]}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={sqrt {frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sum _{i}(Y_{i}-{bar {Y}})^{2}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86595f3f77e8ee96952760d9176a5fa140cc562)




![{displaystyle operatorname {mathbb {E} } left[rright]=rho -{frac {rho left(1-rho ^{2}right)}{2n}}+cdots ,quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/683b838e709e3b32a3c22dfec4fa665a593f42ad)


![{displaystyle r=operatorname {mathbb {E} } [r]approx r_{text{adj}}-{frac {r_{text{adj}}left(1-r_{text{adj}}^{2}right)}{2n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e094c3fdfcb0bfd127f4be74e582f22a407201c4)
![{displaystyle r_{text{adj}}approx rleft[1+{frac {1-r^{2}}{2n}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf3f71f2cfe17f8f0d422d5ac0d482cc429a925)





![{displaystyle operatorname {corr} _{r}(X,Y)={frac {operatorname {mathbb {E} } [,X,Y,]}{sqrt {operatorname {mathbb {E} } [,X^{2},]cdot operatorname {mathbb {E} } [,Y^{2},]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d897e4b303a062ed14cc9f88f35f5c8ffc91f7)