Руководитель:
Пестрожукова Елена Александровна
Учреждение:
ГАПОУ «Нижнеломовский многопрофильный техникум»
В процессе работы над индивидуальным проектом по математике «Геометрическое определение коэффициента комфортности жилья « учениками Нижнеломовского многопрофильного техникума была поставлена и реализована цель выяснить, дом какой формы наиболее комфортен для проживания с точки зрения соотношения объема жилья и его поверхности.
Подробнее о проекте:
В ученической исследовательской работе по математике «Геометрическое определение коэффициента комфортности жилья» автор проводит анализ учебно-методической литературы об истории геометрии и строительства, рассматривает характеристики разных геометрических фигур, а также выясняет особенности применения геометрических норм и правил в строительстве домов.
В готовом творческом и исследовательском проекте по математике «Геометрическое определение коэффициента комфортности жилья» учащимися были выбраны для исследования несколько видов жилищ разных геометрических форм и размеров, определены формулы вычисления объемов и площадей поверхности различных геометрических тел, соответствующих выбранным жилищам. Авторы проекта вычислили коэффициенты комфортности для каждого жилища и выявили жилище наиболее комфортной для проживания формы с точки зрения соотношения объема жилищного пространства и его поверхности.
Оглавление
Введение
1. Геометрия и строительство.
1.1 Применение геометрии в строительстве.
1.2. Геометрические фигуры и тела в строительстве
1.3. Объемы тел и площади поверхностей.
2. Вычисление коэффициента комфортности жилья разной геометрической формы.
Заключение
Список литературы
Введение
«Все вокруг геометрия!»
Ле Корбюзье
Вся жизнь современного человека проходит в тесной связи с математикой. Современная жизнь людей на столько сложна и многообразна, что им постоянно приходиться совершенствовать свою математическую культуру и постоянно при решении насущных проблем обращаться к математике. Куда бы ни кинул взгляд человек – всюду геометрические объекты, всюду геометрия. К тому же место, где человек проводит большую часть своей жизни, его жилище, тоже имеет определенную геометрическую форму.
А каким должен быть дом современного человека? При строительстве любого дома люди всегда задаются вопросом: «Какой дом лучше?». «Лучше тот, что теплее» – скажут одни, «лучше тот, что красивее или комфортнее» — скажут другие. Но есть ли способ определить – это «лучше»? Попробуем ответить на этот вопрос с точки зрения геометрии.
В последнее время все чаще говорят о том, что мировые запасы природных ресурсов небезграничные, остро стоит проблема энергосбережения. Одним из способов сэкономить тепло является обеспечение жилья наименьшей потерей тепла через его поверхность. Можно существенно уменьшить размеры дома, но человек должен иметь достаточно жилого пространства, чтобы чувствовать себя комфортно. Таким образом, встает вопрос: как достичь сочетания максимально возможного объема жилого пространства при минимальной площади поверхности, через которую может уходить тепло. И сейчас этот вопрос остается для человечества особенно актуальным.
В связи с этим была поставлена цель исследования: выяснить, дом какой формы наиболее комфортен для проживания с точки зрения соотношения объема жилья и его поверхности.
Что определило задачи исследования:
- Выбрать для исследования несколько видов жилищ разных геометрических форм и размеров.
- Определить формулы вычисления объемов и площадей поверхности различных геометрических тел, соответствующих выбранным жилищам.
- Вычислить коэффициенты комфортности для каждого жилища.
- Выявить жилище наиболее комфортной для проживания формы с точки зрения соотношения объема жилищного пространства и его поверхности.
Объект исследования: использование геометрии в жизни человека.
Предмет исследования: применение геометрии для определения коэффициента комфортности жилья.
Гипотезаисследования: существует жилище определенной геометрической формы, имеющее наибольший коэффициент комфортности для жизни человека.
Методыисследования:
- наблюдение;
- поиск и отбор информации;
- анализ, исследование, систематизация материала.
Применение геометрии в строительстве
Профессия строителя является очень древней. До наших дней дошло немало сооружений, возраст которых измеряется тысячелетиями. Свой опыт мастера строительного дела передавали из поколения в поколение, в том числе и математические знания. В строительстве никак не обойтись без математики. В современном строительстве роль этой науки непрерывно возрастает. Специалисты должны создавать и перерабатывать чертежи, тексты, документы, таблицы, формулы; выполнять расчеты площадей различных фигур, объёмов многогранников и тел вращения.
Важно отметить и обратную историческую взаимосвязь: потребности зарождающегося строительства и, возникшей вслед за ним архитектуры, явились одним из стимулов, благодаря которым возникла и сделала первые
шаги геометрия. Ни один из видов искусств так тесно не связан с геометрией как архитектура и строительство. Тесная связь геометрии и архитектуры известна с давних времен. Издревле геометрия считалась одним из разделов архитектуры.
Архитекторы утверждают, что геометрия – это основа архитектурного мастерства. С давних времен люди возводя свои жилища думали об их прочности, удобстве, внешнем виде, устойчивости к погодным и климатическим условиям. Прочность сооружения заключается не только в материале, из которого оно сделано, но и в конструкции, используемой при строительстве.
Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы сооружений являются комбинациями различных геометрических тел.
Геометрические фигуры и тела в строительстве
Куб — правильный многогранник, каждая грань которого представляет собой квадрат.
Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани -параллелограммами.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Сфера (от греческого — мяч, шар) — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).
Конус — тело, ограниченное конической поверхностью и кругом основания.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Объемы тел и площади поверхностей
Для измерения объемов и площадей поверхности многогранников и тел вращения используются следующие формулы.
Куб: S_(п.п.)=6а^2 ,V=а^3
Призма: S_(п.п.)=2S_o+S_(б.п.) ,S_(б.п.)=P_(o )∙H ,V=S_o∙H
Пирамида: S_(п.п.)=S_o+S_(б.п.) ,S_(б.п.)=1/2 P_(o )∙d ,V=1/3 S_o∙H
Сфера, шар: S_(п.п.)=4∙π∙R^2 ,V=4/3 (∙π∙R)^3
Конус: S_(п.п.)=S_o+S_(б.п.) S_(б.п.)=π∙R∙l ,V=1/3 (∙π∙R)^2∙H
Цилиндр: S_(п.п.)=2S_o+S_(б.п.),S_(п.п.)=2∙π∙R∙H ,V=(π∙R)^2∙H
Вычисление коэффициента комфортности жилья разной геометрической формы
Жилище – место жизни человека, место, где он рождается, растет. Это кров, укрытие, место покоя и порядка. Жилище как центр человеческой вселенной осознается почти повсеместно. Но в зависимости от образа жизни и места на земном шаре оно имеет большую или меньшую значимость для человека. Вместе с этим каждый человек стремится к более высокому качеству жизни, которое зависит от комфортности условий, обеспечивающих жизнедеятельность человека.
Существует зависимость между комфортом нашего дома и его математическими характеристиками: например, объёмом и площадью. Ученые предложили формулу вычисления комфортности жилища: . Здесь V – объём жилища (например, вашей комнаты) и S – полная поверхность жилища. Самым комфортным считается жильё с коэффициентом k = 1.
Геометрия архитектуры окружающих нас зданий разнообразна. Как известно, разные народы строили для себя жилье разных форм, видимо, строители руководствовались известными им принципами. И почему кот, когда в холодную ночь он приготовляется ко сну, поджимает лапы, свертывается и таким образом делает свое тело насколько возможно шарообразным? Почему так удобно свернуться «калачиком», когда спишь? Видимо, соотношения формы, объема и площади поверхности тел имеют закономерность, влияющую на степень комфортности. Это можно доказать опытным путем. Вычислим коэффициент комфортности жилья разной геометрической формы.
1. Подавляющее число жилых зданий имеет форму куба или прямоугольного параллелепипеда.
Дано: куб с ребром а.
Найти: коэффициент комфортности к
Решение:1)Найдем объем куба: V=a³
2)Найдем площадь полной поверхности: Sп.п.=6а²
3)Найдем коэффициент комфортности к=(36π(а^3 )^2)/(〖6а〗^2 )^3 = (36πа^6)/(216а^6 )=π/6 к=0,52< 1 => жилье формы куба не очень комфортное!
Дано: жилище формы прямоугольного параллелепипеда с измерениями а=8м, b=4м, с=4м.
Найти: коэффициент комфортности к
Решение:
1) Найдем объем прямоугольного параллелепипеда: V= abc =128м³
2) Найдем площадь полной поверхности: Sп.п.=2(ab+bc+ac)=160 м²
3) Найдем коэффициент комфортности к <1, => жилье формы прямоугольного параллелепипеда не очень комфортное!
2. В современном мире существуют здания пирамидальной формы. Причины, по которым человечество древнего мира выбрало для строительства первых высотных зданий форму пирамиды, очевидны. Причина номер один: форму пирамиды подсказала сама природа. Причина номер два: форма пирамиды в строительстве при определенных условиях является самым надежным и крепким сооружением.
Дано: правильная четырехугольная пирамида, а=5 м, H=4 м
Найти: коэффициент комфортности к
Решение:
1. Найдем площадь основания: Sосн.= а2 =25м²
2. Найдем площадь боковой поверхности: Sб.п.= м²
3. Найдем площадь полной поверхности: Sп.п.= Sосн.+ Sб.п =72 м²
4. Найдем объём: V= а2 h =33(3)м³
5. Найдем коэффициент комфортности:
<1, => коэффициент далек от 1, жилье не комфортное!
3. Чум является универсальным жилищем северных народов. Это переносная конусообразная палатка, форма которой является приспособленной, целесообразной для тундры. Форма конуса делает жилище устойчивым при метелях и сильных ветрах, снег с него легко скатывается. Интересно, как чувствует себя человек в доме конусообразной формы с точки зрения комфортности.
Дано: жилище конусообразной формы h=4м, r =3м.
Найти: коэффициент комфортности к
Решение:
1) Найдем объем конуса: V=П r2 h =37,68м³
2) Найдем площадь полной поверхности: Sп.п.= П r2 + П rl =75,36 м²
3) Найдем коэффициент комфортности
К <1, => коэффициент далек от 1, жилье не комфортное!
4. Достаточно знаменит дом Константина Мельникова в Москве — шедевр русского авангарда, входящий во все учебники по архитектуре 20 века. Выбор цилиндрической формы архитектор объяснял тем, что в таком пространстве при отсутствии прямых углов полезная площадь намного больше, чем в традиционных зданиях.
Не менее известен «AquaDom» – это 25-метровый аквариум цилиндрической формы из акрилового стекла, построенный вокруг прозрачного лифта. Он находится в отеле «Radisson SAS Hotel» в Берлине. Вычислим коэффициент комфортности проживания в цилиндрическом доме.
Дано: цилиндр, h=3м, R=2м.
Найти: коэффициент комфортности
Решение: Sполн.п. =2ПR(R+Н)=2·П·2(2+3)=20П≈62,8 м2
V= Sосн. · h =ПR²· h=12П≈37,68 м3
<1, тем не менее, пока это наибольший из полученных коэффициентов.
5. Рассмотрим несколько примеров вычисления коэффициентов комфортности комбинированного жилья.Жилье – прямоугольный параллелепипед – усеченная пирамида;
Дано: а=6м, в=4м, с=8м, а1= 3м, в1=2, h=3.
Найти: коэффициент комфортности к
Решение:
Найдём объём и площадь поверхности параллелепипеда:
V1=abc=192м², S1=6·4+6·8·2+8·4·2=184м²
Найдём объём и площадь полной поверхности усечённой пирамиды
V1 =h*(S+s+√Ss)/3=42м³
Sповерх=Sбок+Sосн =55,2
Найдём объём и полную поверхность комбинации тел
V=V1+V2= 234,2 м², S =239,2м², К=36πv2 S³=0,45<1
Коэффициент комфортности низкий, жилье не комфортно.
Жилье – полусфера – цилиндр.
Дано: R=2, h=5.
Найти: коэффициент комфортности к
Решение: Vцилиндра = ПR2h=251,2 м3,
Vполушара = ПR3=133,973 м3, Vтела=385,17 м3.
Sцилиндра = 2ПRh+ ПR2=175,84 м2, Sполусферы = 4ПR2=100,48 м2, Sтела=276,32 м2 К=36πv2S³=0,7949 < 1
Это наибольший из полученных коэффициентов.
6. Современное строительство предлагает дома сферической формы.
Дано: жилье шарообразной формы радиусом R.
Найти: коэффициент комфортности
Решение: Sсферы.=4 πR2, V=(4πR^3)/3,
С помощью математических расчетов получены следующие результаты комфортности жилья таблица 1:
| №п/п | Вид жилья | Коэффициент комфортности, к |
| 11 | Куб | 0,52 |
| 22 | Прямоугольный параллелепипед | 0,45216 |
| 33 | Пирамида | 0,335 |
| 44 | Конус | 0,375 |
| 55 | Цилиндр | 0,648 |
| 66 | Комбинированное: усеченная пирамида и прямоугольный параллелепипед | 0,45 |
| 77 | Комбинированное: полусфера и цилиндр | 0,79 |
| 88 | Сфера | 1 |
Сравним результаты с помощью диаграммы:
Вывод: У всех жилищ разной формы различный изопериметрический коэффициент комфортности, и существует жилище, имеющее наилучший изопериметрический коэффициент. Дом — сфера имеет самый большой коэффициент комфортности. Дом — сфера комфортен для жилья.
Известно, что природа, в отличие от нашего традиционного строительства, не создаёт сложные, немобильные конструкции и технологии.
Идеальной формой, наиболее близкой природе, как известно, является шар. Преимущества и возможности строительства сфер:
Согласно изопериметрической теореме из всех тел равного объема наименьшую поверхность имеет шар. Это означает, что на шарообразные сооружения нужно материалов меньше, чем на иные.
Прочность сферы обеспечена равномерным распределением нагрузок на все точки поверхности. Она превосходно работает на сжатие и на изгиб.
Сфера является наилучшей формой от ветровых и снеговых нагрузок.
Создание сферы отличает минимальная материалоемкость, трудоемкость и длительность возведения.
Сферическая форма сама по себе является энергосберегающей, к тому же она изготавливается практически бесшовной, что минимизирует теплопотери, и снижает затраты на устройство отопительной системы.
Отсутствие арматуры в стенах.
В сферических сооружениях нет углов, где обычно застаивается воздух, их легче проветривать.
Легкость и прочность сфер обуславливает целесообразность их строительства в сейсмически опасных районах.
Сферу значительно сложнее разрушить взрывами, даже пробитая в одном или нескольких местах, она не теряет своих конструктивных способностей и не «складывается».
Можно создавать сферические многоярусные городские структуры, используя минимальные площади под фундаменты, развивая пространственные композиции.
Заключение
Все вокруг математика! Все вокруг геометрия! И в самом деле — всюду геометрия. Современная цивилизация — это Цивилизация Математики, Геометрии. С помощью геометрии в данной работе исследуется степень комфортности жилья в зависимости от его геометрической формы. Как известно сегодня дом это совсем не роскошь, а настоящая необходимость, причем порой довольно острая. При этом современное жилье с каждым годом претерпевает все более ощутимые изменения, совершенствуясь в своей комплектации и получая все новые и новые возможности.
Исследование подтвердило гипотезу: жилье сферической формы имеет высший коэффициент комфортности. Таким образом, цели и задачи исследования достигнуты.
Очевидно, в скором будущем преимущества сферы будут использованы в архитектуре, и новые города будут содержать дома — сферы, полусферы в комбинации с цилиндрами. Тенденции к округлости форм уже налицо в автомобилестроении, оформлении интерьеров, не заставят себя ждать они и строительстве жилья.
Практическое значение творческой работы. В работе выполнен расчет коэффициента комфортности для различных видов жилья. Решение этой задачи может иметь важнейшее практическое значение и может быть использовано в дальнейшем в архитектуре и строительстве.
Эта работа может быть использована для мотивации к изучению геометрии для студентов первого курса, а так же в рамках недели математики на внеклассных мероприятиях.
Так какой же дом лучше? Безусловно, для каждого человека лучше тот дом, в котором он вырос или живет сейчас. И в этой работе была предпринята попытка сделать маленький шаг навстречу возможности проектировать и строить эти дома уютнее и комфортнее.
Список литературы
- Л.С. Атанасян. Геометрия 10-11, Просвещение, 2003.
- С.Б. Проскуряков. Строители пирамид из созвездия Большого пса, Орел, «Книга», 1992.
- Ван дер Варден. Математика древнего Египта, Вавилона и Греции, Пробуждающая наука. Перевод с голландского И.Н.Веселовского, Москва, 1959.
- Н.А. Заиченко Нужна ли математика в жизни? [Электронный ресурс].
- Б.В. Гнеденко. Математика в современном мире. — М.: Просвещение, 2005. — 177 с.
- Г.И. Глейзер. История математики в школе. — М.: Просвещение, 1984.
- Н. Ф. Гуляницкий. Архитектура гражданских и промышленных зданий в пяти томах. Том I. История архитектуры. – М.: Строиздат.1984.
- А. В. Волошинов. Математика и искусство — М.: Просвещение, 2000.
Если страница Вам понравилась, поделитесь в социальных сетях:
Геометрическое определение коэффициента комфортности жилья
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Языков М.Д. 1
1ГБОУ СОШ №2 г.Сызрани
Калинкина И.М. 1
1ГБОУ СОШ №2 г.Сызрани
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение.
Вся жизнь современного человека проходит в тесной связи с математикой.
Куда бы ни посмотрел человек – везде геометрические объекты, везде геометрия. К тому же место, где человек проводит большую часть своей жизни, его жилище, тоже имеет определенную геометрическую форму и присущие ей свойства.
А каким должен быть дом современного человека? При строительстве любого дома люди всегда задаются вопросом: «Какой дом лучше?». «Лучше тот, что теплее» – скажут одни, «лучше тот, что красивее или комфортнее» — скажут другие и так далее. Тогда зададимся вопросом, есть ли способ определить – это «лучше»? Я решил ответить на вопрос с точки зрения геометрии.
Так появилась цель моей работы: выяснить, дом какой формы наиболее комфортен для проживания с точки зрения соотношения объема жилья и его поверхности.
Глава I.
Идея создания этого проекта появилась во время прогулки по городу. Изначально человек при строительстве дома предполагает его основную геометрическую форму и размеры, а затем появляются еще определенные факторы, которые тоже говорят о комфортности жилья -строй материалы, размещение, внутреннее устройство и т.д.
Задачи исследования:
1. Выбрать для исследования несколько видов жилищ разных геометрических форм и размеров;
2. Определить формулы вычисления объемов и площадей поверхности различных геометрических тел, соответствующих выбранным жилищам;
3. Вычислить коэффициенты комфортности для каждого жилища;
4. Выявить жилище наиболее комфортной для проживания формы, с точки зрения соотношения объема жилищного пространства и его поверхности.
Предмет исследования: применение геометрии для определения коэффициента комфортности жилья.
Гипотеза: возможно определить жилище какой формы обладает наилучшим изопериметрическим коэффициентом комфортности.
Жилище – место жизни человека, это кров, укрытие, место покоя и порядка. В зависимости от того, в какой части света или стране находится человек, его жилище может иметь разную форму и особенности: где-то более тёплое, влагоустойчивое или же более крепкое. В результате в условиях определенного климата и имеющихся строительных материалов у всех народов появились В последнее время все чаще говорят о том, что мировые запасов природных ресурсов небезграничны.
Темпы добычи газа в России — 763 млрд м³ (за 2021 год достигла максимума)национальные жилища.
Доказанные запасы газа России составляют 47,8 трлн м³.
Если мы такими же темпами будем добывать и использовать газ, то, по прогнозам экспертов, газовые месторождения иссякнут через 50-70 лет.
Перед населением планеты давно стоит проблема энергосбережения. Известно, что огромное количество энергии тратится на отопление помещений, в том числе жилых.
Одним из способов сэкономить тепло является обеспечение жилья наименьшей потерей тепла через его поверхность. Можно существенно уменьшить размеры дома, но человек должен иметь достаточно жилого пространства, чтобы чувствовать себя комфортно. Таким образом, встает вопрос: как достичь сочетания максимально возможного объема жилого пространства при минимальной площади поверхности, через которую может уходить тепло. И сейчас этот вопрос остается для человечества актуальным, а с учетом ситуации с энергоносителями становится все более острым. Поэтому выбранная мной тема очень актуальна.
Глава II.
Расчет коэффициентов комфортности жилья
Существует зависимость между комфортом нашего дома и его математическими характеристиками: например, объёмом и площадью. Ученые предложили формулу вычисления комфортности жилища:
V – объём жилища (например, вашей комнаты), S – полная поверхность жилища.
Вычислим коэффициент комфортности жилья разной геометрической формы.
1. Жилище формы прямоугольного параллелепипеда
Дано: жилище формы прямоугольного параллелепипеда с измерениями а=8м, b=4м, с=3м.
Решение:
1. Найдем объем прямоугольного параллелепипеда: V= abc =96м³
2. Найдем площадь полной поверхности: Sп.п.=2(ab+bc+ac)=136 м²
= ≈ 0, 414
3. Найдем коэффициент комфортности:
2. Жилище в форме куба
Дано: куб с ребром а.
Найти: коэффициент комфортности
Решение:
1. Найдем объем куба: V=a³
2. Найдем площадь полной поверхности: Sп.п.=6а²
= = 0,523
3.Найдем коэффициент комфортности:
3. Здание в форме треугольной призмы
Дано: а=6м, с=8м, h=4. Найти: коэффициент комфортности k -?
Решение:
1. Найдём площадь поверхности:
S= (а +6с) = (6 +6·8)= 175,2 м²
· а²с= 6² · 8 =124,7м³
2. Найдём объём:
= ≈ 0, 327
3. Коэффициент комфортности:
a
с
а
4. Здание пирамидальной формы
Дано: жилье в форме правильной четырехугольной пирамиды с измерениями а=5 м, h=4 м
Решение:
1. Найдем площадь основания: Sосн.= а² =25 м²
2. Найдем площадь боковой поверхности:
= 4 ⋅( 4 ⋅ ≈ 47м²
3. Найдем площадь полной поверхности: Sп.п.= Sосн.+ Sб.п =72 м²
4. Найдем объём:
= ≈ 33,(3) м³
5. Найдем коэффициент комфортности:
= ≈ 0, 335
5. Здание конической формы
Чум является жилищем северных народов, конической формы, в
высоту достигает 4 метров, в диаметре 5-6 метров, крытый шкурами, берестой или мешковиной. Форма конуса делает жилище устойчивым при метелях и сильных ветрах, снег с него легко скатывается. Интересно, как чувствует себя человек в доме конусообразной формы с точки зрения комфортности.
Определим коэффициент комфортности жилища конусообразной формы h=4м, r =3м.
Решение:
= ≈ 37,68м³
1. Найдем объем конуса:
2. Найдем площадь полной поверхности:
Sп.п.=Sосн.+Sбок = + = 3,14 3 +3,14 3 = 75,36 м²
= ≈ 0, 375
3. Найдем коэффициент комфортности:
6. Здание цилиндрической формы
Достаточно знаменит дом Константина Мельникова в Москве — шедевр русского авангарда, входящий во все учебники по архитектуре ХХ века. Выбор цилиндрической формы архитектор объяснял тем, что в таком пространстве при отсутствии прямых углов полезная площадь намного больше, чем в традиционных зданиях.
Вычислим коэффициент комфортности проживания в цилиндрическом доме.
Дано: жилье цилиндрической формы, h=3м, r=2м.
Решение:
1. Найдем объем цилиндра:
V= Sосн. · h =r²· h= 2 ·3 =37,68 м³
2. Найдем площадь полной поверхности:
=2 ( + Н) = 2·3,14·2·(2 + 3) =
= ≈ 0, 648
3. Найдем коэффициент комфортности:
7. Жилье формы треугольной усеченной пирамиды
Дано: жилье с параметрами а=8, в=4, h=4,7, L=5
Найти: коэффициент комфортности
Решение:
1. Найдем площадь:
Sполн = Sосн1 + Sосн2 + Sбок = + h)=
= + 4,7)=116 м²
2. Найдем объем:
Sосн1 Sосн2 = м³
= ≈ 0, 418
3. Найдем коэффициент комфортности:
8. Жилье формы четырехугольной усеченной пирамиды
Дано: жилье с параметрами а=8, в=4, h=4,7, L=5
Найти: коэффициент комфортности
Решение:
1. Найдем площадь:
Sполн = Sосн1 + Sосн2 + Sбок =4 а+ ) =
= + )= 189 м²
2. Найдем объем:
Sосн1 Sосн2 =5,5 м³
= ≈ 0, 516
3. Найдем коэффициент комфортности:
9. Жилье формы усеченного конуса
Дано: жилье с параметрами l=10,4, R=5, r=2, h10
Найти: коэффициент комфортности
Решение:
1. Найдем площадь:
Sполн 3,14 )=319,6 м²
=м³
2. Найдем объем:
= ≈ 0, 577
3. Найдем коэффициент комфортности:
Рассмотрим несколько примеров вычисления коэффициентов
комфортности комбинированного жилья.
10. Здание цилиндрической формы с конической крышей
Хижина цилиндрической формы с глиняными стенами, с конической
крышей из камыша — народное жилище Замбии. Высота примерно 3-4 м,
в диаметре достигает 5-6 метров.
Определим коэффициент комфортности жилища цилиндрической
формы с конической крышей Н=2м, h=1,5м, r =2,5м.
Решение:
1. Найдем площадь полной поверхности:
Sбок.кон. = = 3,14 2,5 = 32,04 м²
= S1осн.+Sбок.= +Н = 3,14·2.5 +2·3,14·2.5·2 =5
32,04+51,055=83,065 м²
=1,5+2 м³
2. Найдем объем:
= ≈ 0, 474
3. Найдем коэффициент комфортности:
11. Здание прямоугольный параллелепипед и треугольная призма
Дано: а=10м, в=8м, с=3м, а1= 8м, в1=8, h=10м.
Решение:
1. Найдём площадь полной поверхности:
Sп.п.=Sпарал.+Sпризм= 2вc+2ac+ав + (в +6а)-в1с =403,43 м²
240+277,13=517,12м³
2. Найдём объём поверхности комбинации тел:
= ≈ 0, 46
3. Найдем коэффициент комфортности:
12. Жилье в форме полусферы
Дано: жилье формы полусферы радиусом «r» =2.
Решение:
1. Найдем площадь полной поверхности:
Sполусферы = + Sосн= +=3= 3 =37,68м²
= 16,75
2. Найдём объём:
= ≈ 0, 593
3. Найдем коэффициент комфортности:
13. Жилье шарообразной формы
Дано: жилье шарообразной формы радиусом r.
Найти: коэффициент комфортности
Решение:
1. Найдем площадь сферы:
Sсферы= 4 π r²
= = 1
2. Найдем объем сферы:
3. Найдем коэффициент комфортности:
14. Я просчитал коэффициент комфортности своего жилища.
Наш дом имеет форму прямоугольного параллелепипеда с мансардной крышей
Дано: а=10м, в=11м, с=3м, h=2,6м.
Решение:
1. Найдём площадь полной поверхности:
Sп.п.= 2(10 3+11 3)+10 11+2(10 2,6+11 2,6)+10 11= 236+219,2=455,2 м²
2. Найдём объём поверхности комбинации тел:
10 11 3+10 11 2,6=330+286= 616м³
= ≈ 0, 455
3. Найдем коэффициент комфортности:
С помощью математических расчетов получены следующие результаты комфортности жилья: Таблица 1
|
№ п/п |
Вид жилья |
Коэффициент комфортности |
|
1 |
Прямоугольный параллелепипед |
0,414 |
|
2 |
Куб |
0,520 |
|
3 |
Треугольная призма |
0,327 |
|
4 |
Пирамида |
0,335 |
|
5 |
Конус |
0,375 |
|
6 |
Цилиндр |
0,648 |
|
7 |
Усеченная треугольная пирамида |
0,418 |
|
8 |
Усеченная четырехугольная пирамида |
0,516 |
|
9 |
Усеченный конус |
0,577 |
|
10 |
Комбинированное: цилиндр и конус |
0,474 |
|
11 |
Комбинированное: прямоугольный параллелепипед и треугольная призма |
0,460 |
|
12 |
Полусфера |
0,593 |
|
13 |
Свой дом |
0,455 |
|
14 |
Сфера |
1 |
Сравним результаты с помощью диаграммы (рис. 1):
Вывод: у всех жилищ разной формы различный изопериметрический коэффициент комфортности, и существует жилище, имеющее наилучший изопериметрический коэффициент. Дом — сфера имеет самый большой коэффициент комфортности. Дом — сфера комфортен для жилья.
Преимущества и возможности строительства сфер:
— Сфера является наилучшей формой от ветровых и снеговых нагрузок.
— Сферическая форма сама по себе является энергосберегающей, к тому же она изготавливается практически бесшовной, что минимизирует теплопотери, и снижает затраты на устройство отопительной системы.
— Легкость и прочность сфер обуславливает целесообразность их строительства в сейсмически опасных районах.
— Сферу значительно сложнее разрушить взрывами, даже пробитая в одном или нескольких местах, она не теряет своих конструктивных способностей и не «складывается».
Заключение.
В ходе исследования я определил жилища какой формы наиболее комфортны для проживания с точки зрения соотношения объема жилищного пространства и потери тепла через его поверхность.
Для этого были проведены вычисления изопериметрических коэффициентов жилищ и их сравнение.
Исследование подтвердило гипотезу: возможно определить жилище какой формы обладает наилучшим изопериметрическим коэффициентом комфортности.
Таким образом, цели и задачи исследования достигнуты.
Эта работа может быть использована для мотивации к изучению геометрии на внеклассных мероприятиях.
На сегодняшний день в инструментарии архитекторов есть программы-помощники, они автоматически просчитывают (исходя из заданных климатических показателей и времени суток) теплопотери, освещенность, вентиляцию проектируемого пространства. В них можно двигать стены, окна и собирать нужную по пространству модель. Было бы интересно выяснить, где еще используются изопериметрические свойства фигур.
Так какой же дом лучше? Безусловно, для каждого человека лучше тот дом, в котором он вырос или живет сейчас. И в этой работе была предпринята попытка сделать маленький шаг навстречу возможности проектировать и строить эти дома уютнее и комфортнее.
Я узнал, что в мире существуют дома самых необычных форм:
Дом в форме призмы
Этот коттедж площадью всего 40 м² расположен в сельской местности на ферме в Австралии. Он построен на фундаменте старого сарая, разрушенного ураганом в 2017 году. Дом отличается односкатной крышей, расположенной под углом 30°, на которой установлены солнечные батареи. Они обеспечивают жильцов электричеством.
Дом на длинных ногах
Домик-кабинка в Норвегии стоит на прочном основании — сваях, заглубленных на 6 м. Он устойчив к ветровым нагрузкам несмотря на то, что возвышается над землёй на 8 м и весит 14 тонн. Конструкцию привезли на участок в готовом виде, чтобы процесс строительства не затрагивал окружающий ландшафт.
Дом-шишка
Эти домики построены в Италии среди ценных хвойных деревьев, которые обычно используются для изготовления музыкальных инструментов. Коттеджи предназначены для отдыха и имеют три уровня:
Кривой дом в городе Сопот (Польша)
Этот необычный дом совершенно лишен прямых углов. Он был создан в 2004 году архитекторами Залевским и Шотинским. Вдохновили архитекторов на создание столь смелого сооружения рисунки художников детских книг Пера Оскара Дальберга и Яна Марцина Шанцера.
Пузырьковый дом Пьера Кардена (Франция)
Этот необычный дом построен для такого же необычного хозяина – известного модельера Пьера Кардена – его хорошим другом Анти Ловагом.
Дом-пузырь в Австралии
Э тот особняк необычной формы был построен в 1981 году по проекту архитектора Грэма Бирчалла. Трехэтажная резиденция Bubble House состоит из 11 бетонных шаров-пузырей от 4 до 8 м в диаметре каждый. Шарообразные конструкции образуют в особняке 20 комнат. В доме три уровня, включая подвал. При этом на всю резиденцию всего три спальни и два санузла.
Футуристические дома в Хертогенбос
Жилой район, состоящий из 50 сферических домов, построен по проекту архитектора Дриса Крейкампа. Дома были построены в рамках экспериментального доступного жилья, эти здания легко демонтировать и перевезти. Вес одного шара — всего лишь 1240 килограммов, и каждый из них можно установить даже на стационарной водной платформе
Кубик роттердамский
В 1984 году в славном в Роттердаме вырос необычный кубический объект, состоящий из 40 домов. Автор творения — архитектор Пит Блом.
Корзинка из Огайо
Вот как нужно брендировать собственный офис! Зато ни у кого не возникает сомнения род деятельности американской компании. Здесь из кленовой древесины вручную изготавливаются различные корзины. Здание состоит из 7 этажей, а 160 тонные ручки оснащены специальной системой, позволяющей предотвратить обледенение в зимний период.
Невидимый зеркальный дом в Нью-Йорке
Нью-Йоркская дизайн-студия STPMJ представила проект невидимого дома, зеркальная поверхность которого не сразу позволяет заметить его в лесном ландшафте.
MIRROR HOUSES — самый известный зеркальный дом в мире. Архитектором проекта является Питер Пахлером. Сооружение расположено в Италии, вблизи города Бальцано. Коттедж сдается в аренду всем желающим, для проведения в нем незабываемого уикенда.
Зеркальный дом — архитектурное сооружение все стены которого построены из отражающих зеркал.
Перевернутый дом
Трассенхайд, Германия Этот объект из Германии своим названием точно отображает идею постройки — «Мир, стоящий на голове». Помещение полностью жилое. Это самый настоящий коттедж, где только экстерьер кажется весьма необычным.
Самый маленький дом в мире
Дом Артура Видена — согласно Книге рекордов Гиннеса, официально считается самым маленьким в мире. Построен в 1919 г. Домик площадью 28 кв.м предприимчивый английский подрядчик ухитрился втиснуть в проход между двумя другими домами. Длина строения – 14 м, ширина – 2м, а высота потолков – 2,4 м. При этом, грамотно спроектировав жилище, архитектору удалось разместить на этой площади кухню со складным столом, плитой и стиральной машиной и спальню с кроватью, которая убирается в стену.
В домике имеются ванная и уютная гостиная. Еще семья оборудовала в доме подвал и облагородила территорию внутренним двориком с крохотным садом.
Самый большой частный дом в мире– дом индийского миллиардера Мукеш Амбани и его семьи «Антилия», который находится в Мумбаи. Высота дома – двадцать семь этажей, соответствующих шестидесяти стандартным этажам, в доме девять лифтов. Общая высота здания в 173 м, площадь около 37 000 м² «Антилия» способна выдержать 8-ми бальное землетрясение. На шести этажах расположена парковка, где находится коллекция автомобилей владельца, а седьмой этаж отведен под частный автосервис. Ещё один этаж – это небольшой театр. Далее следуют этажи с бальными залами, бассейнами, спа-салонами, висячими садами. Семья миллионера, в которую входит Мукеш, его мать, жена и трое детей, занимает четыре этажа, а три этажа – шестьсот человек обслуживающего персонала. Над резиденцией находятся 3 вертолётные площадки и центр управления полётами. Главный концепт проекта – смешение архитектурных элементов и стилей, которые будучи последовательно соединёнными, ни разу не повторяются. Нет повторений и в материалах отделки. Самый большой в мире частный дом является одновременно и самым дорогим в мире частным строением.
Какова правильная площадь жилья?
Санитарным законодательством РФ утвержден минимальный размер общей площади жилого помещения – 18 м². Например, для семьи из 4-х человек комфортным считается помещение с площадью жилых комнат 72 м². Также в сумму нужно прибавить около 20-30 м² на:
кухню (20-30 м²)
коридор (4-5 м²);
ванную (4-5 м²);
туалет (2-3 м²);
подсобную комнату (5-7 м²).
В итоге, как показывает несложный расчет, комфортный размер дома для семьи из 4 человек – около 80-90 м². Остальное увеличение площади и, соответственно, размера жилья зависит от личных пожеланий и нужд будущих жильцов.
Анкетирование
После совместной работы я опросил своих одноклассников, понравилось ли им тема «Геометрическое определение коэффициента комфортности жилья» и расчет коэффициентов комфортности. Предложил им ответить на вопросы анкеты:
По результатам анкетирования, я сделал вывод, что моим одноклассникам интересна тема «Геометрическое определение коэффициента комфортности жилья». На кружке по математике можно продолжить работу по расчету коэффициентов комфортности жилья.
В будущем я планирую продолжить изучение данной темы и рассчитать коэффициенты комфортности для сложных конструкций:
Список литературы:
Спивак А.В. Тысяча и одна задача по математике: Кн. для учащихся 5–7 кл.– М.: Просвещение, 2010г.
А.Б. Крыжановский «Изопериметры» М. – Л.,Физматлит, 1959 г. Л.С. Атанасян. Геометрия 10-11, Просвещение, 2003. — 287с.
Н.А. Заиченко Нужна ли математика в жизни? [Электронный ресурс].
Б.В. Гнеденко. Математика в современном мире. — М.: Просвещение, 2005. — 177 с.
Болтянский, В.Г. Наглядная топология / В.Г. Болтянский, В.А.,Ефремович – М.: Наука, 1975. – 160 с.
Глейзер. Г.И. история математики в средней школе / Г.И. Глейзер. – М.: Просвещение, 1970.
Математический энциклопедический словарь / Ю.В. Прохоров [и др.]. –М.: Издательство «Советская энциклопедия», 1988. – 340 с.
Перельман Я.И. «Занимательная геометрия». – М.: АСТ.Астрель, 2003.
Прасолов, В.В. Наглядная топология / В.В. Прасолов. – М.: МЦНМО, 1995. – 110 с.
Старова, О.А. Топология – 2013. – № 9. – с.28-34.
Просмотров работы: 540
Государственное
учреждение образования «Средняя школа №9 г. Слуцка»
КУПОЛ ДОМА ТВОЕГО
Исследовательская работа по математике
Автор работы:
Кашаед Дарья Владиславовна
учащаяся 9 «А» класса
Руководитель:
Тарасова Галина Ивановна
учитель математики
Государственное учреждение образования
«Средняя школа №9 г. Слуцка»
г. Слуцк
2020г.
Содержание
Введение……………………………………………………………………………3
1.Вычисление коэффициента комфортности жилищ различной формы……..5
1.1.
Вычисление коэффициента комфортности жилья
в форме прямоугольного параллелепипеда………………………………………. 5
1.2.
Вычисление коэффициента комфортности жилья
в форме куба………7
1.3.
Вычисление коэффициента комфортности жилья
в форме конуса…….8
1.4.
Вычисление коэффициента комфортности
жилья в форме усеченного конуса………………………………………………………………………10
1.5.
Вычисление коэффициента комфортности жилья
в форме цилиндра..11
1.6.
Вычисление коэффициента комфортности купольного
дома — жилья в форме полусферы и шара …………………………………………..……13
Заключение……………………………………………………………………….16
Список
использованных источников………………………………….………..18
Приложения………………………………………………………………………19
Введение
В одной из телепередач “Прогноз
погоды» я услышала, что в скандинавских странах часто строят малоэтажные дома
сферической формы, т.к. эти дома являются самыми экономичными с точки зрения
соотношения потери тепла и объема жилищного пространства, более устойчивы к
природным катаклизмам и самыми комфортными. Очень усомнилась в экономичности и комфортности
такого жилья. Когда человеку уютно, приятно, спокойно, он говорит, что ему
комфортно.
С помощью интернета убедилась, что
человек создает жилища разнообразной формы. Существуют традиционные жилища
разных народов, а также современные архитектурные сооружения. Возникло много
вопросов, на которые захотелось найти ответы. Существует ли связь между
чувством комфортности и формой жилища? Жилище какой формы наиболее комфортно
для проживания с точки зрения соотношения объема жилья и потери тепла через его
поверхность? Существует ли зависимость между
комфортом нашего дома и его математическими характеристиками: например, объёмом
и площадью? Какой
из народов нашей планеты сумел создать жилище наиболее комфортной формы?
Ответить
на все поставленные вопросы можно вычислив коэффициент комфортности жилищ
различной формы: прямоугольного параллелепипеда, куба, конуса, усеченного
конуса, цилиндра, полусферы и сферы. Опираясь на стереометрическую
изопериметрическую теорему, учеными была получена формула для вычисления
комфортности жилища.
Чтобы
впоследствии узнать, дом, какой формы является наиболее комфортным для
проживания с точки зрения соотношения потери тепла и объема жилищного
пространства, необходимо вычислить и сравнить изопериметрические коэффициенты
жилищ. Назовем этот коэффициент коэффициентом комфортности. Для этого
потребуется формула k
= , где V — объем жилища,
S — площадь полной поверхности. Чем больше коэффициент, тем комфортнее жилище.
Цель исследования:
определить, жилище, какой формы наиболее комфортно для проживания с точки
зрения соотношения объема и площади полной поверхности жилищного пространства.
Задачи:
·
Изучить
теоретический материал по теме работы.
·
Анализ
интернет — ресурсов
·
Вычислить коэффициенты комфортности для жилищ
разной геометрической формы.
·
Сравнить коэффициенты комфортности исходя
из полученных результатов.
·
Найти применение результатам исследования
в повседневной жизни.
Объектом исследования
являются жилища, которые имеют различную геометрическую форму.
Предмет
исследования: изопериметрический коэффициент комфортности жилища.
Гипотеза: жилье
сферической формы имеет наивысший коэффициент комфортности.
Актуальность темы заключается в демонстрации и применении
математических знаний в повседневной практической деятельности человека.
Методы исследования: сбор материала по теме, его анализ и обработка,
математические
расчеты, поиск применения
результатов исследования в повседневной жизни, оформление работы, создание
презентации.
1.Вычисление коэффициента комфортности
жилищ различной формы
Изопериметрический коэффициент комфортности
можно найти по формуле: k = , где V- объем жилища, S
— площадь полной поверхности. Чем больше коэффициент,
тем комфортнее жилище.
Чем
ближе изопериметрический коэффициент геометрического тела к единице, тем ближе
такое жилище к идеальному с точки зрения моего исследования. Это значит, что
жилище, имеющее наибольший изопериметрический коэффициент, — наилучшее с точки
зрения соотношения жилого пространства и поверхности, через которую уходит из
дома тепло.
1.1.
Вычисление коэффициента комфортности жилья
в форме прямоугольного параллелепипеда
В
нашем городе, как и во многих
странах, подавляющее число многоэтажных и одноэтажных домов имеют
форму прямоугольного параллелепипеда. И наш дом, и первый арендный дом в нашем
городе. Такую же форму имеют частные дома не только в нашей стране, но и в
других странах – в Испании, Мексике, Аргентине…(Приложение1). Комнаты
преимущественно тоже в форме прямоугольного параллелепипеда. Используя формулу,
по которой вычисляется коэффициент комфортности жилища, определим наиболее
комфортную комнату в нашей квартире, а так же коэффициент комфортности кабинета
математики и спортивного зала в нашей школе. Сравним коэффициент комфортности
трех комнат, имеющих равную площадь пола и высоту, но различную форму пола.
1.1.1. Зал
в нашей квартире: длина – 6,4м; ширина- 3м, высота –
2,4м.
Вычисление
коэффициента комфортности:
1)Найдем объем прямоугольного параллелепипеда:V=abc=6,4*3*2,4=
46,8(м³)
2) Найдем площадь полной поверхности:
S полн. поверхности
= 2(ab+bc+ac)
= 2(6,4.3+3*2,4+6,4*2,4) = 2(19,2+7,2+15,36) =2*41,76 = 83,52 (м²)
3) Найдем коэффициент комфортности: 

0,425
0,425<1
1.1.2. Моя спальня: длина – 5м; ширина – 3м;
высота – 2,4м.
Вычисление
коэффициента комфортности:
1) Найдем объем прямоугольного параллелепипеда: V= abc
=5*3*2,4=36(м³).
2)Найдем площадь полной поверхности:
S полной поверхности =2(ab+bc+ac)=2(5.3+3*2,4+5*2,4)=
2(15+7,2+12) = 68,4( м²).
3) Найдем коэффициент комфортности: 

0,458.
0,458 < 1.
Оказалось, что при одной и той же ширине и высоте, но при разной
длине коэффициент комфортности разный. 0,425 < 0,458 < 1
1.1.3. Кабинет математики в школе: длина — 8м; ширина —
6м; высота -3.2м.
Вычисление
коэффициента комфортности:
1)
V=a*b*c=6*8*3,2=153,6
(м3)
2)
S=6*3.2*2+3.2*8*2+8*6*2=185,6
(м2)
3)
k = =
0,42 .
0,42 ˂ 1
1.1.4. Спортивный зал нашей школы: длина
-15 м, ширина -8 м, высота-4,2м
Вычисление
коэффициента комфортности:
1)V=4,
20*8*15=504 (м3)
2)S=8*4,
20*2+15*4, 20*2+8*15*2=433, 2 (м2)
3)
k=
=
0, 35.
0,35˂ 1.
1.1.5. Сравним коэффициент комфортности трех комнат,
имеющих равную площадь пола -36м2 и высоту-2.4м, но различную форму
пола.
1.1.5.1. Квадрат со
стороной 6 м.
Вычисление
коэффициента комфортности:
1) V=36*2,4=86,4
(м3)
2) S=6*4*2,4+36*2=57,6+72=129,6
(м2)
3) k=
=
0, 39 ˂
1.
1.1.5.2 Прямоугольник
со сторонами 4м и 9м.
Вычисление
коэффициента комфортности:
V=36*2,4=86,4
(м3)
S=4*2,4*2+9*2,4*2+36*2=19,2
+43,2 +72=134,4 (м2)
k=
=
0, 35 ˂ 1.
1.1.5.3 Прямоугольник со сторонами 2м и 18м.
Вычисление
коэффициента комфортности:
V=36*2,4=86,4
(м3)
S=2*2,4*2+18*2,4*2+36*2
= 9,6 +86,4 +72 = 168 (м2)
k=
=
0, 18˂ 1.
Вывод: коэффициент комфортности жилья в форме прямоугольного
параллелепипеда значительно меньше единицы, коэффициент комфортности комнат,
имеющих равную площадь пола и высоту, но различную форму пола выше, если пол
имеет форму квадрата. Значит, жилье формы прямоугольного параллелепипеда не
очень комфортное.
1.2 Вычисление коэффициента комфортности
жилья в форме куба
Нередко
встречаются дома и помещения в форме куба. Примером могут служить десять отелей
в форме куба, а так же частные дома в Китае, в Ирландии, в Германии, в
Канаде…(Приложение 2)
Так
как коэффициент комфортности жилья в форме куба не зависит от размеров ребра,
вычислим его в общем виде.
Дано: куб с ребром а.
Найти: коэффициент комфортности.
Решение.
1)Найдем объем куба: V= a³.
2)Найдем площадь полной поверхности: Sп.п.=6а².
3)Найдем коэффициент комфортности k= =

0,52˂ 1.
Вывод: коэффициент комфортности
жилья в форме куба меньше единицы, но по сравнению с жильем в форме
прямоугольного параллелепипеда коэффициент комфортности выше. Значит жилье в
форме куба комфортнее.
1.3.Вычисление
коэффициента комфортности жилья в форме конуса
В
разных странах имеются дома в форме конуса. Так коническую форму имеют собор в бразильском городе Маринге, здание в
городе Могила на острове Самосир, здание гостиницы в
Беларуси чум Башня Кутаба в Индии. Жилищем
конической формы является восточносибирский чум. Это переносная конусообразная
палатка, которая достаточно устойчива при сильном ветре и метелях. (Приложение
3). Выясним, комфортно ли в таком
жилище и зависит ли коэффициент комфортности чума от величины высоты и радиуса
основания.
1.3.1. Если радиус, высота и образующая заданы
числами, образующими Пифагорову тройку.
Дано:
высота – 4 м, радиус основания – 3 м, образующая – 5 м.
Вычисление
коэффициента комфортности:
1)
V= * 3,14*32*4=
37,68(м3)
2)
Sбоковой поверхности =
3,14*3*5=47,1 (м2)
3)
Sоснования = 3,14*32
= 28,26 (м2)
4)
S = 47,1 + 28,26 = 75,36 (м2)
5)
k=
=
0,375
0,375˂ 1.
1.3.2. Уменьшим первоначальное значение радиуса на 1 м.
Дано:
высота – 4 м, радиус основания – 2 м, образующая –м.
Вычисление
коэффициента комфортности:
1)V=
* 3,14*22*4=
16,75( м3)
1)
Sбоковой поверхности = 3,14*2*=26,64 (м2)
2)
Sоснования = 3,14*22
= 12,56 (м2)
3)
S = 26,64 + 12,56 = 39,2 (м2)
4)
k=
=
0,53.
0,53˂ 1
1.3.3. Уменьшим высоту в 2
раза.
Дано:
высота – 2 м, радиус основания – 3 м, образующая –м
Вычисление
коэффициента комфортности:
1)
V= * 3,14*32*2= 18,84(
м3)
2)
Sбоковой поверхности = 3,14*3*=
(м2)
3)
Sоснования = 3,14*32
= 28,26 (м2)
4)
S = 33,96 + 28,26 = 75,36 (м2)
5)
k=
0,17.
0,17˂ 1
1.3.4. Если осевое сечение
конуса правильный треугольник.
Дано:
l =a, R=, h =
.
Вычисление
коэффициента комфортности:
1)
V= πR2h
= *π
*
=
2)
Sбоковой поверхности = πRl
=
3)
Sоснования = π =
4)
Sполной поверхности =
5)
k=
=
0,44.
0,44˂ 1
Вывод: коэффициент комфортности
жилья в форме конуса меньше единицы; коэффициент комфортности выше, если
осевое сечение конуса правильный треугольник и высота больше радиуса основания.
Значит жилье в форме конуса комфортнее, если угол наклона образующей к плоскости
основания больше 60о.
1.4.
Вычисление коэффициента комфортности жилья в форме усеченного конуса
Собор
Святого Себастьяна В Рио-де-Жанейро, д-ром Оуэн Гейгер
(Owen Geiger), жилища эвенков имеют форму усеченного
конуса. (Приложение 4). Посчитаем коэффициент комфортности такого
жилища. Проверим зависит ли он от угла наклона образующей к плоскости
основания. Воспользуемся формулами:
Sполной
поверхности = πR12
+π l
(R1+R2
) + πR22
V = πH(R12
+ R1
R2
+ R22)
1.4.1 Дано: R1
= 3м, R2
=2м, H=2,5м.
l
= =
2,70(
м)
Sполной
поверхности=3.14*32+3.14 *2,7(3+2)+3,14*22=28,26+42,39+
12,5683,21(м2)
V = 3,14*
2,5* (9+6+4) 49,72(
м3)
k=
=
0, 49.
0, 49˂ 1
1.4.2 Уменьшим высоту.
Дано:
R1
= 3м, R2
=2м, H=2м
l
= =
2,23(м)
Sполной
поверхности=3.14*32+3.14*2,23*5*3,14*22=28,26+35,01+12,5675,83(м2)
V
= 3,14*
2* (9+6+4) 39,77(
м3)
k=
=
0,41 ˂
1.
1.4.3 Увеличим высоту.
Дано: R1
= 3м, R2
=2м, H=3,5м
l
= =
3,64 (
м)
Sполной
поверхности=3.14*32+3.14*3,64*5*+3,14*22=28,26+57,15+
12,5697,97(м2)
V
= 3,14*
3,5* (9+6+4) 69,60(
м3)
k=
=
0,58 ˂
1.
Вывод: коэффициент комфортности
жилья в форме усеченного конуса меньше единицы; но он выше, коэффициента
комфортности жилья в форме конуса. Комфортнее жилье, если угол наклона
образующей к плоскости основания больше 60о.
1.5. Вычисление коэффициента комфортности
жилья в форме цилиндра
Форма цилиндра достаточно распространена в архитектуре. В форме
цилиндра построены различные башни, высотные дома, кинотеатры, спортивные
сооружения. Примером архитектурных сооружений в форме цилиндра могут быть:
круглый дом Мельникова в Москве, цилиндрический дом в Мадриде, «AquaDom»
–25-метровый аквариум в отеле «Radisson SAS Hotel» в Берлине, здание
из стекла и бетона в Варшаве, жилой комплекс «Авангард» в Москве, вилла в Японии, а
так же юрта – жилище кочевников казахов, монголов, киргизов и жилище народа
Кирди в Камеруне. (Приложение 5). Вычислим коэффициент комфортности
такого жилища.
1.5.1. Традиционные размеры
жилища народа Кирди: радиус основания – 2 м, высота – 6 м.
V=
πR2Н=
3,14* 4 *6= 75,36( м3)
Sполной
поверхности = 2 πR(R+Н)=
2*3,14*2(2+6)= 100,48(м2)
k=
=
0.63 ˂
1.
1.5.2. Рассмотрим влияет ли изменение
высоты на коэффициент комфортности.
Дано: R
= 2 м, h
= 3м
Вычисление
коэффициента комфортности:
V=
π*R2*h
= π * *
3 = 37,68( м3)
Sбоковой
поверхности = 2πRh
= 2*3,14*2*3 = 37,68(м2)
Sоснования
= π =
3,14*4= 12,56(м2)
Sполной
поверхности = 37,68 + 25,12 = 62,8(м2)
k=
=
0, 65 ˂
1.
1.5.3. Увеличим радиус, высоту
оставим прежней.
Дано:R
= 3 м, h
= 3м
Вычисление
коэффициента комфортности:
V=
π*R2*h
= π * *
3 = 84,78( м3)
Sбоковой
поверхности = 2πRh
= 2*3,14*3*3 = 56,52(м2)
Sоснования
= π =
3,14*9= 28,26(м2)
Sполной поверхности = 56,52 + 56,52 = 113,04(м2)
k=
=
0,56 ˂
1.
1.5.4. Рассмотрим
равносторонний цилиндр.
Дано:R
= 2 м, h
= 4м
V=
π*R2*h
= π * *
4 = 50,24( м3)
Sбоковой
поверхности = 2πRh
= 2*3,14*2*4 = 50,24(м2)
Sоснования = π =
3,14*4= 12,56(м2)
Sполной поверхности = 50,24 + 25,12 = 75,36(м2)
k=
=
0,67 ˂
1.
Вывод: коэффициент комфортности
жилья в форме цилиндра меньше единицы, но по сравнению с другими, такое жилье
можно считать достаточно комфортным. Из всех цилиндров наивысший коэффициент
комфортности у равностороннего цилиндра.
1.7.
Вычисление коэффициента комфортности
купольного дома — жилья в форме полусферы и шара
Под купольным
домом принято понимать строительный объект сферической, формы и с закругленной
крышей. Форму шара и полусферы имеют многие архитектурные
сооружения. Первые сферические постройки появились еще в Византии, да и
эскимосы стали создавать свои жилища в условиях экстремально низких температур
еще много лет назад. Северные народы первыми заметили, что сферические
постройки обладают высокой ветроупорностью и сейсмоустойчивостью. Современные
сферические здания выглядят просто невероятно, проекты поражают воображения.
Какслауттанен —
семейная гостиница. Этот уникальный отель с аутентичными номерами — иглу с
панорамной крышей расположился в Полярном круге, в провинции Лапландии в
Финляндии. Аналогичный отель есть в Канаде и еще пяти странах. Номера оснащены
всем необходимым для проживания, а через прозрачную крышу виднеется чистейшее
небо со звездами или северным сиянием. Дачи и частные дома в
Подмосковье, дом-шар в Новосибирске, дома в
Великобритании имеют сферическую форму. 50 сфер на цилиндрических основаниях
стоят в одном месте, образуя особый микрорайон городка Хертогенбос недалеко от
Амстердама. Название поселения — Болвонинген, что означает дом-шар. Этим
сооружениям уже около 40 лет (Приложение 6). Интересно, как чувствует
себя человек в доме сферической формы с точки зрения комфортности..
1.6.1. Вычислим
коэффициент комфортности полусферы.
Дано:R
= 2 м.
Вычисление
коэффициента комфортности:
V=
πR3
Sбоковой
поверхности = 2πR 2
Sоснования
= π
Sполной
поверхности = = 3π
k=
=
0,60 .
0,60 ˂ 1.
1.6.2. Вычислим коэффициент комфортности сферического жилища. Размеры жилища:
радиус – 2 м.
Вычисление коэффициента
комфортности:
1)
V=*3.14*23 =
33,49 м3
2)
S = 4*3.14*22 = 50,24(м2)
3)k=
=
= 0.999980009 ≈1
1.6.3. Вычислим
коэффициент комфортности в общем виде.
V=
πR3
S
поверхности = 4πR 2
k=
=
= 1
Вывод: мы получили наибольший
возможный коэффициент. Купольный дом — сфера наиболее комфортен для жилья.
Заключение.
В процессе моего
исследования я изучила теоретический
материал [1] для вычисления площади и объема геометрических тел,
проанализировала параметры и характеристики жилищ разных народов, вычислила
коэффициент комфортности жилищ различной формы: прямоугольного параллелепипеда,
куба, конуса, усеченного конуса, цилиндра, полусферы и сферы и сравнила
комфортность жилищ разной формы и размеров.
Цель работы
достигнута. Исследование подтвердило гипотезу: Жилье сферической
формы имеет высший коэффициент комфортности. Думаю, что в скором будущем
преимущества сферы будут использованы в архитектуре, и новые города будут преимущественно
содержать дома — сферы, полусферы в комбинации с цилиндрами. Будущее за купольными
сооружениями.
Практическая
значимость моего исследования состоит в том, что сведения,
полученные в ходе выполнения этой работы, может применить любой человек,
который живет в частном доме или имеет загородный дом при постройке беседок,
теплиц, установке подвесных кресел. Эту информацию можно использовать,
отправляясь на отдых при выборе отелей с видом на северное сияние, кемпингов,
палаток, а так же при выборе детских домиков-палаток и жилья для своих
питомцев. (Приложение 7).
Материал данной работы можно рекомендовать к
использованию на уроках математики или на факультативных занятиях в качестве
дополнительного материала с целью появления у учащихся заинтересованности к
учебному предмету и пробуждения желания к изучению математики, а также для
расширения их кругозора.
Считаю,
что интересно и полезно продолжить расчеты исследованием более сложных форм и
фигур.
В процессе исследования комфортности
жилища я испытала интеллектуальную комфортность — это удовлетворенность
своей мыслительной деятельностью и ее результатами, а также удовлетворение
потребности в получении новой информации.
Список используемых источников
1.
В.В. Шлыков
«Геометрия 11», Минск, «Народная асвета» 2013г.
2.
А. М.
Абрамов, Н.Я. Виленкин, Г.В. Дорофеев, и др. Избранные вопросы математики
10 кл.: Факультативный курс. М.: Просвещение 1980
3.
https://m-strana.ru/articles/kupolnyy-dom/
4. melnikovasv.ucoz.ru›_ld/0/41
5. http://festival.1september.ru/articles/525352/http://www. rugbc. org/ru/resources/articles/izvseh—tel—ravnogo—ob—ema—naimenshaya—poverhnost—u—shara melnikovasv. ucoz. ru›_ld/0/41 http://festival.1september. ru/articles/525352/ http://www. /books/000738756344d1ef668c1
6.
дома-сферы фото
7. жилища народов мира с
названиями
Приложения
Приложение
1

Дом в Слуцке Первый
арендный дом в Слуцке

Частный дом в Испании Загородный
дом в Аргентине
Приложение
2



дом в Китае Частный дом в Ирландии Частный дом в Германии

Дом в Канаде
Десять отелей в форме куба
Приложение
3


Здание гостиницы в
Беларуси Собор
в Бразилии

Здание
на острове Самосир
Приложение
4

д-ром Оуэн
Гейгер Собор Святого Себастьяна в Рио-де Жанейро

Жилище эвенков
Приложение
5


Варшава,
Польша Дом
Мельникова


в Японии


жилище кочевников Частный дом в Швеции
казахов, монголов,
киргизов


Жилища народов кирди в Камеруне
Деревня в Северной Кении
Приложение
6


дом в Подмосковье Дом-шар в Новосибирске

Дома-шары в голландском городе Хертогенбос



Дома-шары изнутри Иглу




семейная гостиница Дача в
Подмосковье
в финской Лапландии
Приложение
7
Детские
домики-палатки


Кемпинговый отдых


В Украине в
Беларуси в Тульской обл. РФ
Беседки и
подвесные кресла



Номера-иглу в
Финском отеле
Домики
для питомцев


«Дух геометрического, математического
порядка будет хозяином судеб
архитектуры» (Ле Корбюзье)
Тема:
2022 год
Цель проекта:
- Обобщение знаний учащихся о свойствах площадей и объемов геометрических фигур;
- Формирование умений применять данные формулы при решении задач практического характера;
- Усвоение навыков коллективной работы при решении задач;
- Развитие пространственных представлений, образного мышления.
Задачи проекта:
- Вспомнить изученные ранее основные характеристики геометрических тел (призмы, пирамиды, конуса, цилиндра, шара и композиций из этих фигур);
- Показать применение данных формул при решении задач практического характера и вычислении коэффициента комфортности жилища;
- Оформить результаты работы в виде коллективной презентации.
Этапы работы над проектом:
- 1 этап – создание рабочих групп, определение целей и задач проекта, планируемых результатов, распределение работы между учащимися в группах;
- 2 этап – поиск необходимой информации, подбор иллюстраций, теоретического материала, решение задач практического характера;
- 3 этап — оформление результатов работы в виде презентации;
- 4 этап – защита коллективного творческого проекта, подведение итогов проекта.
Проблема: жильё какой формы самое комфортное?
Коэффициент комфортности жилья:
Формирование групп
- 1 группа – исследование многогранников и
комбинаций геометрических фигур
.
- 2 группа – исследование тел вращения и
комбинаций геометрических фигур
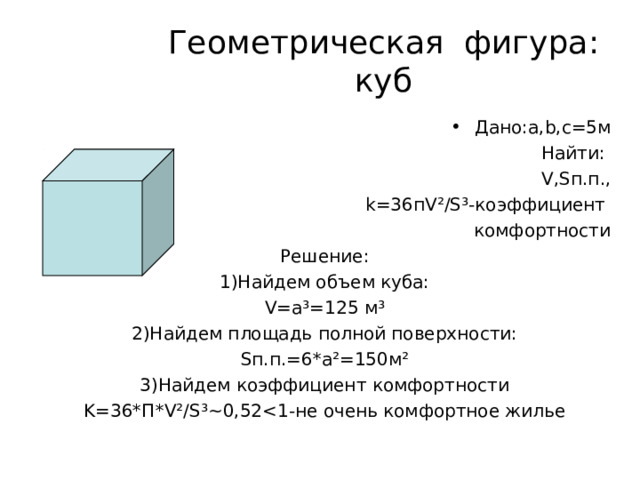
Геометрическая фигура: куб
- Дано: a , b , c=5 м
Найти:
V,S п.п.,
k=36 п V ²/S³- коэффициент
комфортности
Решение:
1)Найдем объем куба:
V=a ³ =125 м ³
2)Найдем площадь полной поверхности:
S п.п.=6*а ² =150м ²
3)Найдем коэффициент комфортности
K=36* П *V²/S³~0, 52
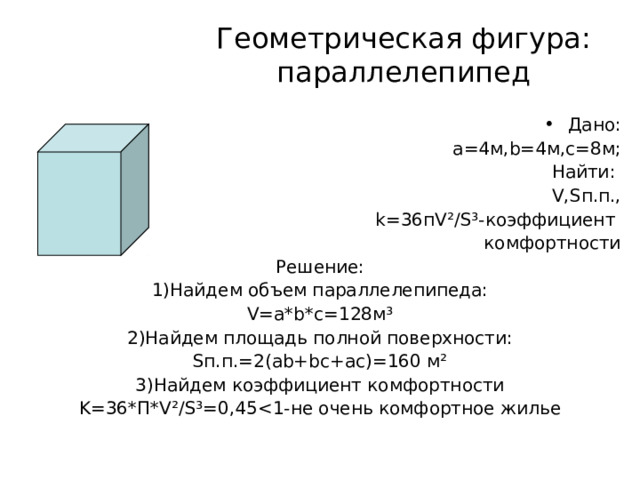
Геометрическая фигура: параллелепипед
- Дано:
а =4 м, b=4 м,с=8м;
Найти:
V,S п.п.,
k=36 п V ²/S³- коэффициент
комфортности
Решение:
1)Найдем объем параллелепипеда:
V=a *b*c=128 м ³
2)Найдем площадь полной поверхности:
S п.п.=2( ab+bc+ac) =160 м ²
3)Найдем коэффициент комфортности
K=36* П *V²/S³=0,45
Архитектурные сооружения в форме параллелепипеда и куба
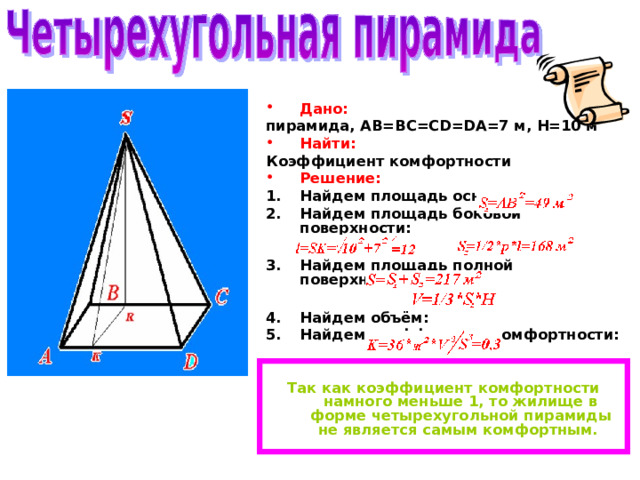
- Дано:
пирамида, AB=BC=CD=DA=7 м, H=10 м
- Найти:
Коэффициент комфортности
- Решение:
- Найдем площадь основания:
- Найдем площадь боковой поверхности:
- Найдем площадь полной поверхности:
- Найдем объём:
- Найдем коэффициент комфортности:
Так как коэффициент комфортности намного меньше 1, то жилище в форме четырехугольной пирамиды не является самым комфортным.
Египетские пирамиды
Комбинация геометрических фигур: прямоугольный параллелепипед и усечённая пирамида.
- Дано:
- а=6м, в=4м, с=8м
- а1= 3м, в1=2, н=3
- Найти : к
- решение:
- Найдём объём и площадь поверхности параллелепипеда:
- V1=abc=192 м ²
- S1p*c+a*b=184 м ²
- Найдём объём и площадь полной поверхности усечённой пирамиды
См. продолжение
Решение
- =h*(S+s+√Ss)/3=42 м ³
- =S бок+ S осн
- S бок=49,2
- =S бок+ S осн = 55,2
- найдём объём и полную поверхность комбинации тел
- V=V1+V2=234 , 2 м ²
- S= + =239 ,2м ²
- К=36 π vS³=0,45
Геометрическая фигура: конус
Дано: R=1 ,5м, H=3 м, L=3 ,4м
Найти: S п.п., V , K -коэффициент комфортности.
Решение:
1) Найдем площадь полной поверхности :
S п.п. = П R(R+L)=23 ,079м ²≈ 23,08 м ²
2)Найдем объем:
V=1/3 П R² * H≈7 ,07М ³
3) Найдем коэффициент комфортности:
K=36 п R²/S³≈0 ,46
значит жилье такой
формы не очень комфортное.
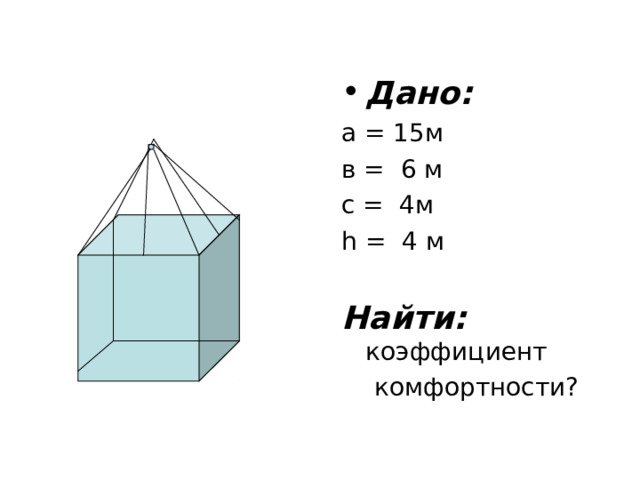
«Архитектурные» сооружения в форме конуса
- Дано:
а = 15м
в = 6 м
с = 4м
h = 4 м
Найти: коэффициент
комфортности?
Решение:
- Найдем объем и площадь поверхности параллелепипеда:
V = a * b * c = 450 м ³
S = 300 м ²
2) Для пирамиды найдём сначала L :
L1=5 м, L2=7 ,5 м
Найдём объём и площадь поверхности пирамиды: V =⅓ S осн * h = 120 м ³
S =120м ²
Найдём объём и площадь поверхности комбинации из геометрических тел: V=V1+V2=570 м ³
S=S1+S2= 420 м ²
Продолжение решения:
- 4) Найдём коэффициент комфортности:
- К=36* π * V²/S³ =0,49
- Вывод:
Жильё такой формы не очень комфортно.
Биг-Бен — едва ли не самые знаменитые в мире башенные часы.
Расположены в башне с восточной стороны Вестминстерского дворца
в городе Лондон
Благовещенская башня Московского Кремля.
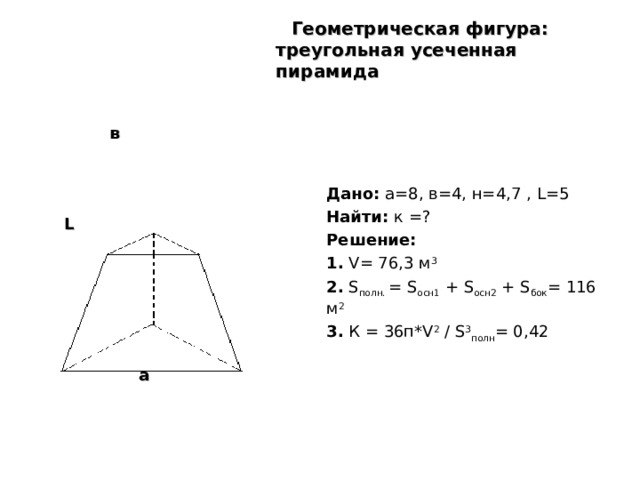
Геометрическая фигура: треугольная усеченная пирамида
в
Дано: а=8, в=4, н=4,7 , L=5
Найти: к =?
Решение:
1. V= 76,3 м 3
2. S полн. = S осн1 + S осн2 + S бок = 116 м 2
3. К = 36п* V 2 / S 3 полн = 0,42
L
а
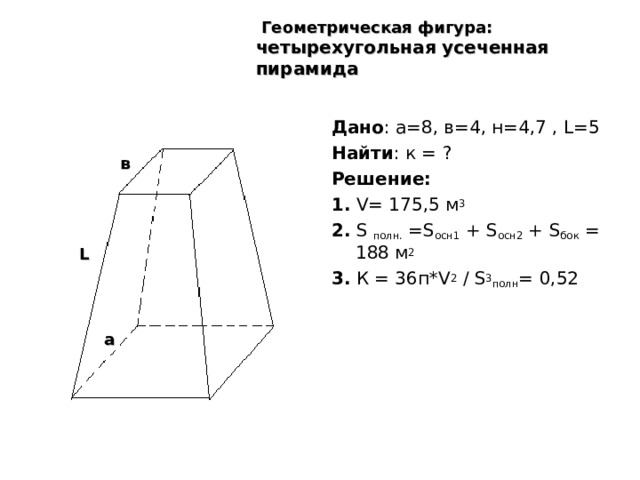
Геометрическая фигура: четырехугольная усеченная пирамида
Дано : а=8, в=4, н=4,7 , L=5
Найти : к = ?
Решение:
1. V= 175,5 м 3
2. S полн. =S осн1 + S осн2 + S бок = 188 м 2
3 . К = 36п* V 2 / S 3 полн = 0,52
в
L
а
- Дано:
Н=10 м, R1=5 м, R 2 = 2 м.
- Найти:
коэффициент комфортности
- Решение:
- Найдем образующую усеченного конуса:
- Найдем объем усеченного конуса:
- Найдем площадь поверхности усеченного конуса:
- Найдем К- коэффициент комфортности:
Комбинация геометрических фигур: цилиндр и усеченный конус
Дано: h=2 м , H=3 м ,r=3 м , R=6 м
Найти: коэффициент комфортности.
Решение: l =3,6
Найдем площадь и объем усеченного конуса:
=129,96 м
=118,7м
Найдем площадь и объем цилиндра:
=226,08м
=339,12м
=0,53 1
L
h
H
Геометрическая фигура: цилиндр.
- Дано : H=3 м., R=2 .
- Найти : S полн.п. ,V.
- Решение:
- S полн.п. = 2П R ( R +Н)
- V = S осн. * Н=П R ² *Н
- V = 3.14*4*3=37,68
- К= 36П V ² / S ³~ 160492,2/247673,15 ~ 0,65
- 0,65
- Ответ: 0,65.
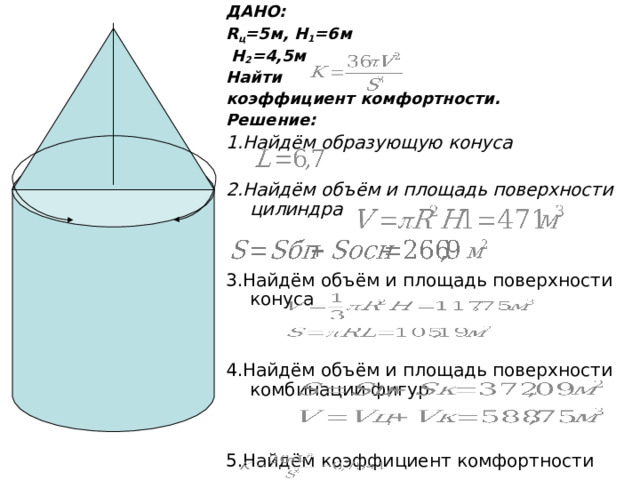
ДАНО:
R ц =5м, H 1 =6 м
H 2 =4,5 м
Найти
коэффициент комфортности.
Решение:
1.Найдём образующую конуса
2.Найдём объём и площадь поверхности цилиндра
3.Найдём объём и площадь поверхности конуса
4.Найдём объём и площадь поверхности комбинации фигур
5.Найдём коэффициент комфортности
Архитектурные сооружения в форме комбинации: конуса и цилиндра
Комбинация геометрических фигур: прямоугольный параллелепипед и треугольной призмы.
- Дано
- а=8,в=10,с=3
- А1=6,в1=10,с1=8
- Найти S полн, V, K.
- Решение
- V=abc=240 м ²
- V 2 =S осн *Н=179,2м ²
S осн = √ p(P-a)(P-b)(P-c)=82,24
V=V 1 +V 2 =419,2 м ²
S 1 =(8+10)*3+8*10=134 м ²
S 2 =2 S осн (6*10)*2=155,84 м ²
S=S 1 +S 2 289,84 м ²
K=36 π V²S³=o,82
Полусфера и цилиндр
R=4
H=5
R=5
Здания в мире
Города будущего
Данная презентация поможет при:
- Обобщении знаний о свойствах площадей и объемов геометрических фигур;
- Формировании умений применять данные формулы при решении задач практического характера.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Слайд 1
Бурангулова Алина, ученица 11 «А» класса Лицей «СИНТОН» самое комфортное жилье
Слайд 2
Цель работы: Обобщение знаний о свойствах площадей и объемов геометрических фигур; Формирование умений применять данные формулы при решении задач практического характера
Слайд 3
Часто можно слышать расхожую фразу: «Круг и шар – наиболее совершенные фигуры». Какой смысл вкладывается в это высказывание? В планиметрии есть теорема: «Из всех изопериметрических плоских фигур наибольшую площадь имеет круг». Иначе: «Из всех плоских фигур равной площади наименьший периметр имеет круг ». Аналогом в стереометрии этой теоремы будет теорема: «Из всех тел равного объёма наименьшую поверхность имеет шар». Изопериметрическое неравенство для объёмных тел будет записано так : V – объём тела, S – площадь полной поверхности.
Слайд 4
Формула для вычисления комфортности жилища : К – изопериметрический коэффициент; V – объём жилища; S – площадь поверхности.
Слайд 5
Восточносибирского чума: H =4 м, R =3 м. H R «Рассчитайте коэффициент комфортности»
Слайд 6
H R Жилища народов кирди в Камеруне: R =2м, H =6м.
Слайд 7
Нашего обычного жилища: a = 6 м , b = 3 м , c = 2,7 м а b с
Слайд 8
К=1 независимо от радиуса.
Слайд 9
Изопериметрический коэффициент К всегда меньше 1 или равен ей. Единственное тело, имеющее коэффициент, равный 1, — это шар