Как найти коэффициент гомотетии если - AvtoShod.ru

Гомотетия с центром (O) и коэффициентом (k) — это преобразование, в котором каждая точка (P) отображается такой точкой

P1,чтоOP1→=k⋅OP→,гдеk≠0

Гомотетия — это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).

Для гомотетичных фигур

в силе формулы отношения периметров

PF1PF=k

и площадей

SF1SF=k2

подобных фигур.

Интересно: любые две окружности гомотетичны.

Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент. Это можно записать: гомотетия ((O; k)).

На рисунке из фигуры

можно получить фигуру

гомотетией ((O; 2)).

Если фигуры находятся на противоположных направлениях от центра гомотетии, то коэффициент отрицательный.

На следующем рисунке из фигуры

можно получить фигуру

гомотетией ((O; — 2)).

Центр гомотетии может находиться и внутри фигуры. Серый треугольник из зелёного треугольника (ABC) получен гомотетией

O;12

Гомотетия ((O; -1)) — это центральная симметрия или поворот на (180) градусов, в данном случае фигуры одинаковые.

В отличие от гомотетии, геометрические преобразования — центральная симметрия, осевая симметрия, поворот, параллельный перенос — являются движением, т. к. в них фигура отображается в фигуру, равную данной.

Гомотетичные фигуры подобны, но подобные фигуры не всегда гомотетичны (в гомотетии важно расположение фигур).

Источник

Гомотетия

Подробности: Категория: Геометрия

Документальные учебные фильмы. Серия «Геометрия».

Преобразование плоскости называется преобразованием подобия или просто подобием, если существует такое число , что для любых двух точек А и В и их образов А’ и В’ выполняется равенство . Число называется коэффициентом подобия.
При =1 преобразование подобия сохраняет расстояния, т. е. является движением. Следовательно, движение — частный случай преобразования подобия. Рассмотрим пример преобразования подобия, отличного от движения.
Зададим точку М₀ и вещественное число . Каждой точке М плоскости поставим в соответствие точку М’ так, чтобы

(1)

Такое отображение является преобразованием плоскости и называется гомотетией. Точка М₀ называется центром гомотетии, а число m — коэффициентом гомотетии. Докажем, что гомотетия — преобразование подобия. Действительно, пусть М₁, М₂ — произвольные точки плоскости, а и — их образы. Из равенства (1) получаем: , поэтому

. (2)

Отсюда получаем: . Таким образом, гомотетия с коэффициентом m является преобразованием подобия с коэффициентом подобия .
При m = 1 из равенства (1) получаем: . Отсюда следует, что любая точка М плоскости совпадает с ее образом, т. е. гомотетия с коэффициентом m = 1 является тождественным преобразованием. При m = — 1 из равенства (1) получаем, что гомотетия — центральная симметрия. В остальных случаях (т. е. когда ) гомотетия — преобразование подобия, отличное от движения, т. е. преобразование плоскости, не сохраняющее расстояния между точками.

Выберем ортонормированный репер (О, Е₁, E₂) так, чтобы точка О совпала с центром гомотетии. Если М (х, у) —произвольная точка плоскости, а точка M′ (х’, у’) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии:
. (3)

Рассмотрим простейшие свойства гомотетии.

1) Гомотетия с коэффициентом переводит прямую, не проходящую через центр гомотетии, в параллельную ей прямую, а прямую, проходящую через центр гомотетии, — в себя.

□ Пусть Ах+Ву+С = 0 — уравнение данной прямой . Подставив сюда значения х, у из (3), получаем уравнение образа этой прямой: Ах’+By’+Сm = 0. Этим уравнением определяется прямая. Если С ≠ 0, то ||, а если С = 0, то и совпадают.

2) Гомотетия сохраняет простое отношение трех точек.

□ Пусть А, В и С — три точки прямой, а А′, В’ и С’ — их образы, и . По определению простого отношения трех точек имеем: . По формуле (2) получаем: , где m — коэффициент гомотетии. Следовательно, . Таким образом, , т. е. (АВ, С) = (А’В’, С’).

Из этих свойств следует, что гомотетия переводит отрезок в отрезок, луч в луч и полуплоскость в полуплоскость.

3) Гомотетия переводит угол в равный ему угол.

□ Пусть ВАС — данный угол, а В′ А′ С’ — образы точек В, А и С. По формуле (2) получаем:

. (4)

Отсюда следует, что

4) Гомотетия сохраняет ориентацию плоскости.

□ Пусть (А, В, С) — произвольный репер, а (А′, В’, С’) — его образ. Используя формулы (4), получаем: . Итак, в гомотетии любой репер и его образ ориентированы одинаково, т. е. гомотетия сохраняет ориентацию плоскости.

Нетрудно доказать, что если и — преобразования подобия с коэффициентами и , то — преобразование подобия с коэффициентом . Действительно, является преобразованием плоскости. Докажем, что для любых двух точек А и В и их образов A’ = () (А), B’ = () (В) выполняется равенство A’B’=AB. Если А₁=(А), B₁=(B), то А’ = (А₁), B’ = (B₁). По определению подобия А₁В₁ = АВ, А’В’ = A₁B₁, поэтому А’В’ = AB.

Теорема 1. Пусть — преобразование подобия с коэффициентом , a h — гомотетия с тем же коэффициентом и с центром в произвольной точке М₀. Тогда существует одно и только одно движение такое, что

. (5)

Рассмотрим преобразование

(6)

Оно является преобразованием подобия с коэффициентом , т.е. движением. Из равенства (6) получаем: , или . Таким образом, существует движение , удовлетворяющая условия (5).

Пусть теперь — произвольное движение, удовлетворяющее равенству . Отсюда получаем: . Учитывая равенство (6), мы приходим к выводу, что = .

Гомотетия обладает всеми свойствами 1° — 8° движений. Доказанная теорема позволяет заключить, что и преобразование подобия обладает теми же свойствами. Следовательно, имеет место утверждение: преобразование подобия прямую переводит в прямую, параллельные прямые — в параллельные прямые, сохраняет простое отношение трех точек, полуплоскость переводит в полуплоскость, отрезок — в отрезок, луч — в луч. Преобразование подобия угол переводит в равный ему угол, а перпендикулярные прямые — в перпендикулярные прямые.
Итак, доказано, что любое преобразование подобия можно представить в виде (5): , где — движение, a — гомотетия. Так как сохраняет ориентацию плоскости, т. е. любой репер переводит в репер той же ориентации, то если сохраняет ориентацию плоскости, то, очевидно, и сохраняет ориентацию плоскости, а если меняет ориентацию плоскости, то и меняет ориентацию плоскости. Таким образом, любое преобразование подобия либо сохраняет ориентацию плоскости, либо меняет ее ориентацию. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода.

Пусть — преобразование подобия коэффициентом . Выберем прямоугольную систему координат и найдем аналитическое выражение преобразования в системе . Для этого рассмотрим гомотетию с центром О и коэффициентом и воспользуемся теоремой 1. Пусть — движение, удовлетворяющее равенству (5). Запишем в системе аналитические выражения преобразований и :

Таким образом, если М (х, у) — произвольная точка плоскости, а М'(х′, у’) — ее образ в преобразовании то

(7)

где =1, если — преобразование подобия первого рода, и = — 1, если — преобразование подобия второго рода. Используя формулы (7), докажем теорему.

Теорема 2. Любое преобразование подобия, отличное от движения, имеет одну и только одну неподвижную точку.

□ Пусть равенства (7) — аналитическое выражение данного преобразования подобия. Точка М (х, у) является неподвижной точкой этого преобразования тогда и только тогда, когда

Рассмотрим определитель этой системы. Если =1, то , а если = — 1, то . Таким образом, при для любого имеем: . Отсюда следует утверждение теоремы.
Следствие. Любое преобразование подобия, имеющее более чем одну неподвижную точку или не имеющее неподвижных точек, является движением.
Используя доказанную теорему и ее следствие, можно провести классификацию преобразований подобия в зависимости от наличия неподвижных точек и инвариантных прямых.
А. Классификация преобразований подобия первого рода. Пусть f — преобразование подобия первого рода. Если f имеет более чем одну неподвижную точку или не имеет неподвижных точек, то по следствию предыдущей теоремы оно является движением, поэтому — параллельный перенос.
Остается рассмотреть случай, когда преобразование с коэффициентом имеет только одну неподвижную точку, которую обозначим через О. Пусть — гомотетия с коэффициентом и центром О. По теореме 1 существует такое движение , что . Так как и — подобия первого рода, то — движение первого рода, причем . Таким образом, — поворот вокруг точки О. Возможны три случая.

1) — тождественное преобразование. В этом случае , т. е. — гомотетия с положительным коэффициентом , .

2) — центральная симметрия. Ясно, что в этом случае — гомотетия с отрицательным коэффициентом .

3) — вращение на угол ; . В этом случае является произведением гомотетии на вращение . Оно называется центрально-подобным вращением.
Центрально-подобное вращение
Таким образом, преобразование подобия, имеющее только одну неподвижную точку, является либо гомотетией с коэффициентом , либо центрально-подобным вращением.

В. Классификация преобразований подобия второго рода. Пусть — преобразование подобия второго рода. Если имеет более чем одну неподвижную точку или не имеет неподвижных точек, то по аналогии со случаем А мы приходим к выводу, что преобразование является либо осевой симметрией, либо скользящей симметрией.
Рассмотрим случай, когда преобразование подобия с коэффициентом имеет только одну неподвижную точку О. Ясно, что , так как в противном случае — движение второго рода, но оно не может иметь только одну неподвижную точку. Пусть — гомотетия с коэффициентом к и центром О. По теореме 1 , где — движение второго рода. Точка О — неподвижная точка движения , поэтому — осевая симметрия. В этом случае называется центрально-подобной симметрией.
Центрально-подобная симметрия
Итак, существует шесть типов преобразования подобия, которые приведены в следующей таблице:

Таблица типов преобразования подобия

Преобразование пространства называется преобразованием подобия или просто подобием, если существует такое число , что для любых двух точек А и В и их образов А’ и В’ выполняется равенство . Число называется коэффициентом подобия.
При преобразование подобия сохраняет расстояния, т. е. является движением. Следовательно, движение — частный случай подобия. Примером преобразования подобия, отличного от движения, является гомотетия, которая в пространстве вводится точно так же, как и в плоскости. Зададим точку М₀ и вещественное число . Каждой точке М поставим в соответствие точку М’ так, чтобы

(1)

Это отображение называется гомотетией с центром Мо и коэффициентом m. Для двух точек M₁ и М₂ и их образов и из формулы (1) получаем:

(2)

Отсюда следует, что . Таким образом, гомотетия с коэффициентом m является преобразованием подобия с коэффициентом .
Выберем ортонормированный репер (О, Е₁, Е₂, Е₃) так, чтобы точка О совпала с центром гомотетии. Если М (х, у, z)—произвольная точка пространства, а точка М’ (х′, у′, z′) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии в пространстве:
(3)

Пользуясь формулами (3), можно доказать, что гомотетия переводит плоскость (прямую), не проходящую через центр гомотетии, в параллельную плоскость (прямую), а плоскость (прямую), проходящую через центр гомотетии,— в себя. Аналогично, пользуясь формулой (2), убеждаемся в том, что гомотетия сохраняет простое отношение трех точек. Отсюда следует, что гомотетия переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость и полупространство — в полупространство. Из формулы (2) следует также, что гомотетия переводит угол в равный ему угол.
Докажем, что гомотетия с коэффициентом m сохраняет ориентацию пространства, если , и меняет его ориентацию, если . Действительно, пусть (А, В, С, D) — произвольный репер, а (А′, В’, С’, D’) — его образ. По формуле (2) получаем: , , поэтому

Отсюда и следует сформулированное выше утверждение.

Теорема 1, сформулированная и доказанная (см. выше), полностью переносится на пространство, т. е. любое преобразование подобия пространства с коэффициентом является произведением гомотетии с тем же коэффициентом и произвольным центром на некоторое движение. Отсюда следует, что подобие пространства переводит плоскость (прямую) в плоскость (прямую), параллельные плоскости (прямые) —в параллельные плоскости (прямые). Подобие сохраняет простое отношение трех точек, поэтому оно переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость, полупространство — в полупространство. Подобие переводит угол в равный ему угол, взаимно перпендикулярные прямые (плоскости) — во взаимно перпендикулярные прямые (плоскости).
Точно так же, как и на плоскости, можно доказать, что любое преобразование подобия либо сохраняет ориентацию пространства, либо меняет ее. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода. Таким образом, гомотетия с положительным коэффициентом является преобразованием подобия первого рода, а гомотетия с отрицательным коэффициентом (в частности, центральная симметрия, ) — преобразованием подобия второго рода.

Источник

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

$[O{A_1} = k cdot OA,]$

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

$[O{A_1} = k cdot OA]$

$[O{B_1} = k cdot OB]$

$[O{C_1} = k cdot OC]$

$[O{D_1} = k cdot OD]$

и соединить вершины A1, B1, C1и D1 отрезками.

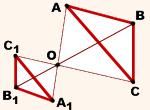
При k<0 гомотетия называется обратной ( точки A и A1лежат по разные стороны от точки O).

гомотетия с коэффициентом k<0

Чтобы построить треугольник, гомотетичный данному треугольнику ABC с центром гомотетии в точке O и коэффициентом k, k<0, нужно провести лучи, выходящие из вершин треугольника, проходящие через точку O, отложить на них отрезки соответствующей длины:

$[O{A_1} = k cdot OA]$

$[O{B_1} = k cdot OB]$

$[O{C_1} = k cdot OC]$

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Источник

§ 8.Гомотетия и подобие пространства

8.1. Определение гомотетии пространства

Рис. 44

Пусть О — данная точка пространства, k — данное число, k ≠ 0. Зададим следующее отображение пространства на себя. Образом произвольной точки М пространства будем считать такую точку М′, что = k (рис. 44).

Точка М имеет единственный образ — точку M′. Более того, из равенства ′ = k находим = ′. Это означает, что точка M′ имеет единственный прообраз — точку М, которая получается, если вектор ′ умножить на число . Следовательно, мы имеем биективное (взаимно-однозначное) отображение пространства на себя, т. е. преобразование пространства, которое называют гомотетией с центром О и коэффициентом k. Заметим, что точка О отображается сама на себя.

Определение. Гомотетией пространства с центром О и коэффициентом k ≠ 0 называется преобразование пространства, при котором любая точка М отображается на такую точку М′, что ′ = k .

Гомотетию с центром O и коэффициентом k обозначают .

Если при этой гомотетии точка М отображается на точку М′, то пишут (М) = M′ или М′ = (М) и говорят, что точка М′ гомотетична точке M. Аналогично определяются гомотетичные фигуры.

При k = 1 гомотетия является тождественным преобразованием, а при k = –1 — центральной симметрией с центром в центре гомотетии.

Из равенства ′ = k находим = ′, откуда следует, что точка М является образом точки M′ при гомотетии с центром О и коэффициентом . Это означает, что преобразование, обратное гомотетии , есть гомотетия с тем же центром О и коэффициентом, равным : ()–1 = .

Изучите взаимное расположение точек О, А и А′ = (А) при:

— k < 0;

— 0 < k < 1;

— k = 1;

— k > 1.

Рис. 45

Рассмотрим композицию двух гомотетий и с общим центром О и коэффициентами k1 и k2 (k1 ≠ 0, k2 ≠ 0).

Пусть M — произвольная точка пространства. Тогда образом точки М при гомотетии является такая точка M′, что M′ = k1. При последующей гомотетии образом точки M′ является такая точка М″, что ″ = k2′ (рис. 45).

Имеем ″ = k2′ = (k2•k1) = (k1•k2). Из этого равенства следует, что точка М отображается на точку M″ при гомотетии с центром О и коэффициентом, равным k1•k2, т. е. (М) = M″.

Таким образом, композицией двух гомотетий с общим центром O и коэффициентами k1 и k2 является гомотетия с центром О и коэффициентом k1•k2: ∘ = .

В частности, ∘ = ∘ = = = E, т. е. композиция двух гомотетий с общим центром и взаимнообратными коэффициентами является тождественным преобразованием.

8.2. Формулы и свойства гомотетии пространства

Выведем формулы гомотетии с центром в начале координат и коэффициентом k.

Рис. 46

Пусть М(х; у; z) — произвольная точка пространства, M′(x′; y′; z′) — её образ при гомотетии (рис. 46).

По определению гомотетии ′ = k . Это векторное равенство в координатной форме равносильно системе равенств

x′ = kx, y′ = ky, z′ = kz. (1)

Соотношения (1) называются формулами гомотетии с центром в начале координат и коэффициентом k.

Теорема 7. При гомотетии с коэффициентом k расстояние между точками изменяется в | k | раз.

Доказательство. Рассмотрим гомотетию . Пусть A(x1; y1; z1), C(x2; y2; z2) — данные точки; A′(; ; ), C′(; ; ) — их образы при гомотетии .

На основании формул (1) имеем

= kx1, = ky1, = kz1; = kx2, = ky2, = kz2. (2)

Тогда для расстояний A′C′ и АС, учитывая (2), получаем

| A′C′ | = =

= =

= | k|• = | k|•| AC|.

Теорема доказана. ▼

Теорема 8. При гомотетии плоскость отображается на параллельную ей или совпадающую с ней плоскость.

Доказательство. Прямоугольную систему координат Охyz выберем так, чтобы её начало O совпадало с центром гомотетии, и рассмотрим плоскость α, заданную в этой системе координат уравнением

Ax + By + Cz + D = 0.(3)

Точка М(х; у; z), координаты х, у, z которой удовлетворяют уравнению (3) плоскости α, при гомотетии отображается на некоторую точку М′ (х′; у′; z′) (рис. 47).

Рис. 47

Согласно (1), x′ = kx, y′ = ky, z′ = kz. Выразив из этих формул переменные х, у, z и подставив их значения в уравнение (3), получим уравнение A + В + С + D = 0.

Преобразуем его к виду

Ax′ + B y′ + Cz′ + kD = 0. (4)

Уравнение (4), которому удовлетворяют координаты точки М′, задаёт некоторую плоскость α′. Это означает, что образом плоскости при гомотетии является плоскость.

Перейдя к обычным обозначениям переменных (без штрихов), получаем следующее уравнение плоскости α′:

Ах + By + Cz + kD = 0.

Из уравнений плоскостей α и α′ следует, что эти плоскости или параллельны (при D ≠ 0), или совпадают (при D = 0), так как обе они имеют один и тот же нормальный вектор (А; В; С). Теорема доказана. ▼

Следствие 1. При гомотетии прямая отображается на параллельную ей или совпадающую с ней прямую.

Рис. 48

Доказательство. Пусть прямая a является пересечением двух плоскостей α и β: α = α ∩ β. При гомотетии плоскости α и β отображаются на некоторые плоскости α′ и β′, причём α′ параллельна α или совпадает с ней, β′ и β также параллельны или совпадают (рис. 48). Так как любое преобразование отображает пересечение фигур на пересечение их образов, то прямая a пересечения плоскостей α и β отобразится на прямую пересечения плоскостей α′ и β′. Обозначим a′ = α′ ∩ β′. Учитывая взаимное расположение плоскостей α′ и α, а также плоскостей β′ и β, получаем: прямая a′ параллельна прямой a, либо с ней совпадает, что и требовалось доказать. ▼

Перечислим ещё некоторые свойства гомотетии:

—при гомотетии величина плоского угла сохраняется;

—при гомотетии величина двугранного угла сохраняется;

—при гомотетии образом многогранного угла является равный ему многогранный угол;

—отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии;

—гомотетия с положительным коэффициентом не меняет ориентации тетраэдра (пространства), а с отрицательным коэффициентом — меняет.

Впоследствии мы узнаем, что отношение объёмов гомотетичных фигур равно модулю куба коэффициента гомотетии.

 ЗАДАЧА (1.123). РАВС — правильный тетраэдр. Построить его образ при гомотетии: 1) с центром С и коэффициентом, равным: а) 2; б) ; в) –; г) –1; 2) с центром в центре грани АВС и коэффициентом, равным: а) ; б) –1.

Решение. Предварительно рассмотрим следующий вопрос. Пусть при гомотетии с центром О точка М отображается на точку M′. (М) = M′. Тогда: 1) ↑↓ ′, т. е. точка О лежит между точками M′ и М (рис. 49, a); 2) | ′ | = | |, т. е. расстояние от точки M′ до точки О в два раза меньше расстояния от точки М до точки О.

Принимая это во внимание, решим задачу 1 (пункт в): центром гомотетии является вершина С данного тетраэдра РАВС. Сначала строим точки A′ = (A), B′ = (B), P′ = (Р) (рис. 49, б), при этом заметим, что центр С гомотетии отображается на себя: (С) = (С), а отрезок АВ при этой гомотетии отображается на параллельный ему отрезок А′B′, причём A′B′ = АВ.

Для остальных рёбер тетраэдра РАВС имеем:

(ВС) = B′C, B′C = ВС, точка B′ лежит на прямой ВС;

Рис. 49

(АС) = A′C, A′C = АC, точки A, A′, C лежат на одной прямой;

(AP) = A′P′, A′P′ = AP, A′P′ || AP;

(BP) = B′P′, B′P′ = BP, B′P′ || BP;

(CP) = CP′, CP′ = CP, точка P′ лежит на прямой СP.

Так как точки А, В, С, Р не лежат в одной плоскости, то точки A′, B′ С, P′ также не лежат в одной плоскости. Соединив отрезками прямых попарно эти точки, получаем тетраэдр P′A′B′C′, который гомотетичен данному тетраэдру РАВС. При гомотетии :

(тетраэдр РАВС) = тетраэдр P′A′B′C.

Грани тетраэдра P′A′B′C являются образами соответствующих граней тетраэдра РАВС:

(△ ABC) = △ A′B′C, (△ ABP) = △ А′В′Р′,(△ BCP) = △ B′CP′, (△ ACP) = △ A′CP′.

При этом соответствующие грани данного и построенного тетраэдров лежат в параллельных плоскостях или в одной плоскости.

8.3.Подобие пространства. Разложение подобия в композицию гомотетии и движения

Подобие с коэффициентом k обозначают символом Pk.

Определение. Подобием пространства с коэффициентом k (k > 0) называется такое преобразование пространства, при котором расстояние между любыми двумя точками изменяется в k раз, т. е. для любых двух точек А и В длина отрезка A′B′ равна k•| AB |, где A′ = Pk(А) и B′ = Pk(В).

Подобие пространства называют также подобным преобразованием пространства или преобразованием подобия пространства.

Если при этом подобии фигура F отображается на фигуру F′, то пишут Рk(F) = F′ и говорят, что фигура F′ подобна фигуре F.

Можно убедиться, что преобразование подобия пространства существует.

В самом деле, любое движение пространства есть подобие с коэффициентом k = 1; любая гомотетия пространства с коэффициентом k > 0 есть подобие с тем же коэффициентом; гомотетия с коэффициентом k < 0 есть подобие с коэффициентом | k|. Далее, композиция g ∘ гомотетии с коэффициентом k и движения g является подобием с коэффициентом | k |, так как расстояния между точками, изменённые в | k | раз при гомотетии, остаются таковыми при последующем движении.

Аналогично, композиция ∘ g движения g и гомотетии также является подобием с коэффициентом | k |.

Справедливо и обратное утверждение.

Теорема 9. Подобие с коэффициентом k можно разложить в композицию движения и гомотетии с некоторым центром и тем же коэффициентом.

Доказательство. Пусть Рk — данное подобие пространства.

Рассмотрим гомотетию пространства с некоторым центром А и коэффициентом Композиция подобия с коэффициентом k и гомотетии с коэффициентом не изменяет расстояния между точками, поэтому является движением пространства.

Композиция ∘ гомотетий с общим центром А и взаимно обратными коэффициентами k и является тождественным преобразованием Е: ∘ = Е. Тогда получаем: ∘ Pk = g, g — движение ⇔ ∘ ( ∘ Pk) = ∘ g ⇔ ( ∘ ) ∘ Pk = ∘ g ⇔ E ∘ Pk = ∘ g ⇔ Pk = ∘ g, что и требовалось доказать. ▼

Так как подобие есть композиция движения и гомотетии, а гомотетия и движение отображают прямые, плоскости, отрезки, лучи соответственно на прямые, плоскости, отрезки, лучи, то при подобии прямые, плоскости, отрезки и лучи отображаются также на прямые, плоскости, oтрезки и лучи соответственно.

Более того, при подобии сохраняется величина угла (плоского и двугранного), параллельные прямые (плоскости) отображаются на параллельные прямые (плоскости), перпендикулярные прямая и плоскость — на перпендикулярные прямую и плоскость.

Справедливость этих утверждений можно доказать, используя теорему 9. Проделайте это самостоятельно.

Из сказанного выше следует, что при подобном преобразовании пространства образом любой фигуры является «похожая» на неё фигура, т. е. фигура, имеющая такую же форму, что и отображаемая (данная) фигура, но отличающаяся от данной лишь «своими размерами».

Рассмотрим вопрос о композиции двух подобий с коэффициентами k1 и k2.

Пусть А и C — данные точки пространства. Если при подобии точки А и С отображаются соответственно на точки A′ и C′, а при последующем подобии точки A′ и C′ — на точки соответственно А″ и C″, то | A′C′ | = k1| AC |, | A″C″ | = k2| A′C′ |. Поэтому | A″C″ | = k2| A′C′ | = k2(k1| AC |) = (k1•k2)| AC |, т. e. при композиции двух подобий с коэффициентами k1 и k2 расстояние между точками изменяется в k1•k2 раз. Но подобие с коэффициентом k1•k2 изменяет расстояние между точками также в k1•k2 раз.

Из сказанного следует, что композиция двух подобий с коэффициентами k1 и k2 есть подобие с коэффициентом k1•k2:

∘ = .

Далее найдём преобразование, обратное подобию Pk.

Пусть это преобразование отображает точки А и C соответственно на точки А′ и C′. Тогда | A′C′ | = k| АС |, откуда | АС | = | A′C′ |. Из этого равенства следует, что точки A′ и C′ отображаются на точки соответственно А и С при подобии с коэффициентом . Но точки А′ = Pk(А) и C′ = Рk(С) отображаются на свои прообразы — точки А и С — преобразованием, обратным подобию Рk. Поэтому преобразованием, обратным подобию Pk, является подобие с коэффициентом :

= .

Заметим, что тождественное преобразование является подобием с коэффициентом k, равным 1. Это означает, что любая фигура подобна самой себе.

Таким образом, а) композиция двух подобий является подобием; б) преобразование, обратное подобию, есть подобие; в) тождественное преобразование — подобие.

8.4. О подобии фигур в пространстве

Вопрос о подобии фигур в пространстве можно рассматривать с точки зрения преобразований подобия, введя следующее определение.

Определение. Фигура F1 называется подобной фигуре F, если существует подобие пространства, отображающее фигуру F на фигуру F1.

Если фигура F1 подобна фигуре F, то пишут: F1 ∾ F.

Рассмотрим свойства отношения подобия фигур.

1. Если фигура F2 подобна F1, то существует подобие Рk, которое фигуру F1 отображает на фигуру F2. Тогда подобие с коэффициентом фигуру F2 отображает на фигуру F1. Теперь по определению подобных фигур фигура F1 подобна фигуре F2.

Таким образом, получили

F2 ∾ F1 ⇒ F1 ∾ F2.

В таком случае говорят, что отношение подобия фигур обладает свойством симметричности.

2. Пусть фигура F1 подобна фигуре F (F1 ∾ F), а фигура F2 подобна фигуре F1 (F2 ∾ F1). Это означает, что существуют такие два подобия и , что F1 = (F) и F2 = (F1). Тогда (F1) = ((F)) = ( ∘ ) (F) = (F) = F2, т. е. композиция подобий и фигуру F отображает на фигуру F2. Но композиция двух подобий есть подобие. Следовательно, фигура F2 подобна фигуре F.

Таким образом, получаем

F1 ∾ F, F2 ∾ F1 ⇒ F2 ∾ F.

В этом случае говорят, что отношение подобия фигур обладает свойством транзитивности.

3. Так как тождественное преобразование есть подобие с коэффициентом k = 1, то любая фигура подобна самой себе: F ∾ F. В этом случае говорят, что отношение подобия фигур обладает свойством рефлексивности.

Свойства рефлексивности, симметричности и транзитивности отношения подобия фигур позволяют разбить множество всех фигур пространства на подмножества — попарно непересекающиеся классы подобных между собою фигур: каждый класс представляет собой множество всех подобных друг другу фигур пространства. При этом любая фигура пространства принадлежит одному и только одному из этих классов.

Например, множество всех кубов — один класс, множество всех правильных тетраэдров — другой класс подобных между собой фигур.

Замечательным является тот факт, что все фигуры одного и того же класса обладают одними и теми же геометрическими свойствами с точностью до подобия (имеют одинаковую форму, но отличаются размерами: отношение площадей подобных фигур равно квадрату коэффициента подобия; далее мы узнаем, что отношение объёмов подобных фигур равно кубу коэффициента подобия).

Для изучения геометрических свойств фигур какого-либо класса достаточно изучить эти свойства произвольно выбранной (любой) фигуры этого класса: такими же свойствами (с точностью до подобия) обладают все фигуры этого класса.

Задания для работы с интернет-ресурсами

Наберите в поисковой строке каждое из указанных ниже движений пространства. Изучите каждое движение, набирая следующий комплект ключевых понятий, составляющими которого являются: «преобразование пространства», «определение движения», «картинки, иллюстрирующие данное движение», «неподвижные точки, прямые и плоскости движения», «род движения», «запись в координатах», «обратное преобразование».

1. Наберите в поисковой строке: «центральная симметрия пространства», «центрально-симметричные фигуры». Далее изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

2. Наберите в поисковой строке: «симметрия относительно плоскости», «зеркальная симметрия», «фигуры, симметричные относительно плоскости». Изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

3. Наберите в поисковой строке: «параллельный перенос». Изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

4. Найдите в поисковой системе темы: «композиция движений», «взаимосвязь различных движений», «движения первого и второго рода в пространстве», «ориентация в пространстве», «семь различных видов движений пространства». Далее изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

5. При помощи материалов, найденных в поисковой системе, узнайте больше о таких движениях, как: «скользящая симметрия», «зеркальный поворот», «винтовое движение». Далее изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

6. Узнайте из Интернета больше о жизни и научной деятельности Мишеля Шаля.

7. Наберите в поисковой строке: «гомотетия в пространстве», «подобие в пространстве». Далее изучите материал в соответствии с каждым из составляющих комплекта ключевых понятий.

8. Посмотрите в поисковой системе «применение преобразований плоскости для построения графиков функций», «преобразования графиков функций», «применение геометрии в алгебре».

9. Узнайте из материалов Интернета сведения о применении движений, особенно симметрий, в физике, химии, биологии, филологии и других науках. Постарайтесь найти как можно больше интересных рисунков, видеороликов и учебных фильмом, посвящённых этой теме. Предложите посмотреть их на ваших уроках.

10. Все, кому интересна геометрия, наберите в поисковой строке слова «топология», «топологически эквивалентные фигуры». Не являются ли топологически «родственными» кружка и тор, окружность и замкнутая ломаная из трёх звеньев, сфера и поверхность куба?

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2.Что нового вы узнали из этой главы?

3.Как могут пригодиться вам эти знания в повседневной жизни?

4.Какие задания главы были для вас самыми трудными? Почему?

5.Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6.Обращались ли вы за помощью к одноклассникам, родителям, учителю?

Источник

Гомотетия

Не пропустите также: