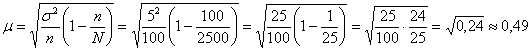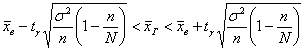11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Коэффициент
доверия позволяет вычислить предельную
ошибку выборки,
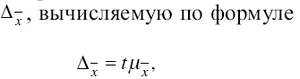
т. е.
предельная ошибка выборки равна
t-кратному числу средних ошибок выборки.
Таким
образом, величина предельной ошибки
выборки может быть установлена с
определенной вероятностью. Как видно
из последней графы табл. 6.1, вероятность
появления ошибки равной или большей
утроенной средней ошибки выборки, т. е.
крайне
мала и равна 0,003(1–0,997). Такие маловероятные
события считаются практически
невозможными, а потому величину
можно
принять за предел возможной ошибки
выборки.
Выборочное
наблюдение дает возможность определить
среднюю арифметическую выборочной
совокупности и величину предельной
ошибки этой средней, которая показывает
(с определенной вероятностью), насколько
выборочная величина может отличаться
от генеральной средней в большую или
меньшую сторону. Тогда величина
генеральной средней будет представлена
интервальной оценкой, для которой нижняя
граница будет равна

Интервал,
в который с данной степенью вероятности
будет заключена неизвестная величина
оцениваемого параметра,
называют доверительным, а
вероятность Р
– доверительной вероятностью. Чаще
всего доверительную вероятность
принимают равной 0,95 или 0,99, тогда
коэффициент доверия t равен
соответственно 1,96 и 2,58. Это означает,
что доверительный интервал с заданной
вероятностью заключает в себе генеральную
среднюю.
Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается
иотносительная
ошибка выборки,
которая определяется как процентное
отношение предельной ошибки выборки к
соответствующей характеристике
выборочной совокупности:
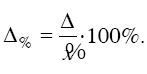
Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем, следовательно, ниже
точность оценки. Средняя (стандартная)
ошибка выборки зависит от объема выборки
и степени вариации признака в генеральной
совокупности.
Определение необходимой численности выборки
Одним
из научных принципов в теории выборочного
метода является обеспечение достаточного
числа отобранных единиц. Теоретически
необходимость соблюдения этого принципа
представлена в доказательствах предельных
теорем теории вероятностей, которые
позволяют установить, какой объем единиц
следует выбрать из генеральной
совокупности, чтобы он был достаточным
и обеспечивал репрезентативность
выборки.
Уменьшение
стандартной ошибки выборки, а следовательно,
увеличение точности оценки всегда
связано с увеличением объема выборки,
поэтому уже на стадии организации
выборочного наблюдения приходится
решать вопрос о том, каков должен быть
объем выборочной совокупности, чтобы
была обеспечена требуемая точность
результатов наблюдений. Расчет
необходимого объема выборки строится
с помощью формул, выведенных из формул
предельных ошибок выборки (Δ), соответствующих
тому или иному виду и способу отбора.
Так, для случайного повторного объема
выборки (n) имеем:
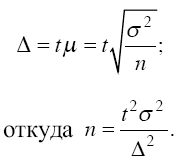
Суть
этой формулы – в том, что при случайном
повторном отборе необходимой численности
объем выборки прямо пропорционален
квадрату коэффициента доверия (t2) и
дисперсии вариационного признака (σ2) и
обратно пропорционален квадрату
предельной ошибки выборки (σ2). В
частности, с увеличением предельной
ошибки в два раза необходимая численность
выборки может быть уменьшена в четыре
раза. Из трех параметров два (t и σ)
задаются исследователем. При этом
исследователь исходя из цели
и
задач выборочного обследования должен
решить вопрос: в каком количественном
сочетании лучше включить эти параметры
для обеспечения оптимального варианта?
В одном случае его может больше устраивать
надежность полученных результатов (t),
нежели мера точности (σ), в другом –
наоборот. Сложнее решить вопрос в
отношении величины предельной ошибки
выборки, так как этим показателем
исследователь на стадии проектировки
выборочного наблюдения не располагает,
поэтому в практике принято задавать
величину предельной ошибки выборки,
как правило, в пределах до 10 %
предполагаемого среднего уровня
признака. К установлению предполагаемого
среднего уровня можно подходить по
разному: использовать данные подобных
ранее проведенных обследований или же
воспользоваться данными основы выборки
и произвести небольшую пробную выборку.
Наиболее
сложно установить при проектировании
выборочного наблюдения третий параметр
в формуле (5.2) – дисперсию выборочной
совокупности. В этом случае необходимо
использовать всю информацию, имеющуюся
в распоряжении исследователя, полученную
в ранее проведенных подобных и пробных
обследованиях.
Вопрос
об определении необходимой численности
выборки усложняется, если выборочное
обследование предполагает изучение
нескольких признаков единиц отбора. В
этом случае средние уровни каждого из
признаков и их вариация, как правило,
различны, и поэтому решить вопрос о том,
дисперсии какого из признаков отдать
предпочтение, возможно лишь с учетом
цели и задач обследования.
При
проектировании выборочного наблюдения
предполагаются заранее заданная величина
допустимой ошибки выборки в соответствии
с задачами конкретного исследования и
вероятность выводов по результатам
наблюдения.
В
целом формула предельной ошибки
выборочной средней величины позволяет
определять:
-
величину
возможных отклонений показателей
генеральной совокупности от показателей
выборочной совокупности; -
необходимую
численность выборки, обеспечивающую
требуемую точность, при которой пределы
возможной ошибки не превысят некоторой
заданной величины; -
вероятность
того, что в проведенной выборке ошибка
будет иметь заданный предел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.6. Оценка генеральной средней по повторной и бесповторной выборкам
Итак, вникаем: пусть из нормально распределенной (или около того) генеральной совокупности
объёма проведена выборка объёма
и по её результатам найдена выборочная средняя
. Тогда доверительный интервал для оценки
генеральной средней имеет вид:
, где
(«дельта» большая) – точность
оценки, которую также называют предельной ошибкойвыборки.
Точность оценки рассчитывается как произведение – коэффициента доверия
на среднюю ошибкувыборки
(«мю»).
Если известна дисперсия генеральной совокупности , то коэффициент доверия
отыскивается из лапласовского соотношения
, а средняя ошибка рассчитывается по формуле:
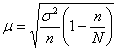
– для повторной.
Если же генеральная дисперсия не известна, то в качестве её приближения используют исправленную выборочную дисперсию . В этом случае коэффициент доверия
определяют с помощью распределения Стьюдента, а при
можно использовать соотношение
. Средняя же ошибка рассчитывается по аналогичным формулам:
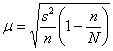
– для повторной выборки.
Напоминаю, что доверительная вероятность (надёжность) задаётся наперёд и показывает, с какой вероятностью построенный
доверительный интервал накрывает истинное
значение .
С конспектом отмучились, теперь задачи 
Модифицируем задание Примера 19, а именно уточним способ отбора попугаев:
Пример 25
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . По результатам 4%-ной бесповторной выборки объёма
, найдена выборочная средняя
(условно средний рост птицы).
1) Найти доверительный интервал для оценки генеральной средней с надежностью
.
2) Выборку какого объёма нужно организовать, чтобы уменьшить данный интервал в два раза?
Не решение даже, а целое исследование впереди, начинаем. Прежде всего, найдём объём генеральной
совокупности:
попугаев, и на самом деле нам предстоит
ответить на следующий вопрос: а достаточно ли выборки объёма ? Или для качественного исследования роста попугаев нужно выбрать побольше
птиц?
1) Доверительный интервал для оценки генеральной средней составим по формуле:
, где
– точность оценки. В задачах данного типа у коэффициента доверия часто
опускают подстрочный индекс и пишут просто ,
однако я не буду следовать мейнстриму, т. к. эта «кастрация» ухудшает понимание.
По условию, нам известна генеральная дисперсия, поэтому коэффициент доверия найдём из
соотношения . По таблице значений функции Лапласа либо на макете (пункт 1*) определяем, что этому значению функции соответствует аргумент
.
Поскольку выборка бесповторная, то среднюю ошибку рассчитаем по
формуле:
Таким образом, точность оценки и
соответствующий доверительный интервал:
– с вероятностью
данный интервал накроет истинное значение генерального среднего
роста попугая.
Теперь предположим, что нас не устраивает точность полученного результата. Хотелось бы уменьшить интервал. Или оставить
его таким же, но повысить доверительную вероятность. Этим вопросам и посвящён следующий пункт решения:
2) Выясним, сколько попугаев нужно взять, чтобы уменьшить полученный интервал в два раза. Иными словами, была точность
0,96, а мы хотим . При условии сохранения
доверительной вероятности необходимый объём выборки можно рассчитать по формуле 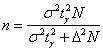
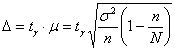
А нашей задаче:
и обязательно проверочка:
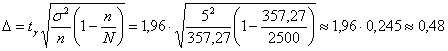
Таким образом, чтобы обеспечить точность при
надёжности нужно провести выборку объёмом
не менее 358 попугаев (округлили в бОльшую сторону). В этом случае получится доверительный
интервал в два раза короче:
И внимание! Здесь нельзя использовать значение предыдущего пункта! Почему? Потому что в новой выборке мы почти
наверняка получим НОВУЮ выборочную среднюю. Вот её-то и нужно будет подставить.
Осталось прикинуть, а не много ли это – 358 попугаев? Объём выборки составит: от генеральной совокупности – ну, в принципе, сносно, хотя и многовато. Поэтому здесь
можно использовать другой подход: оставить точность оценки прежней, но повысить доверительную вероятность до
. В этом случае нужно найти новый коэффициент доверия
(из соотношения
) и решить уравнение
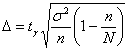
. Желающие могут выполнить этот пункт самостоятельно, в результате
получается выборка в попугаев или
генеральной совокупности. Что лучше, конечно, ведь измерить
линейкой 358 попугаев – задача хлопотная, они явно будут сопротивляться, а некоторые ещё и говорить нехорошие слова J.
Теперь распишем доверительный интервал подробно:
и ответим вот на какой вопрос: а что будет, если генеральная совокупность великА или даже бесконечна? В
этом случае дробь близкА к нулю, и мы получаем
интервал:
, который фигурировал в Примере 19. То есть по
умолчанию (когда не сказано, бесповторная выборка или нет), считают именно так.
Следует отметить, что полученный выше интервал соответствует повторной выборке со
средней ошибкой , таким образом, при слишком
большом объёме генеральной совокупности
математическое различие между бесповторной и повторной выборкой стирается.
Пришло время запланировать собственное статистическое исследование:
Пример 26
В результате многократных независимых измерений некоторой физической величины в прошлом достаточно точно определена генеральная дисперсия
ед.; при этом средняя величина склонна изменениям (от исследования к
исследованию). Сколько измерений нужно осуществить, чтобы с вероятностью заключить текущее истинное значение генеральной средней
в интервале длиной 0,5 ед.
И это как раз только что описанный случай: данную выборку можно считать бесповторной, при этом ген. совокупность
теоретически бесконечна; либо повторной, так как округлённые результаты измерений могут повторяться.
Краткое решение в конце книги, числа можете выбрать по своему вкусу J. Но здесь есть одно «странное» значение . Оно не случайно и соответствует
правилу «трёх сигм», т. е.,
практически достоверным является тот факт, что построенный интервал накроет истинное значение .
Разумеется, на практике генеральная дисперсия чаще не известна, и поэтому за неимением лучшего, используют исправленную
выборочную дисперсию:
Пример 27
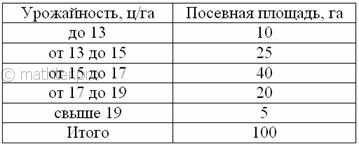
С целью изучения урожайности подсолнечника в колхозах области проведено 5%-ное выборочное обследование 100 га посевов,
отобранных в случайном порядке, в результате которого получены следующие данные:
С вероятностью 0,9974 определить предельную ошибку выборки и возможные границы, в которых ожидается средняя
урожайность подсолнечника в области.
Решение: в условии не указан тип отбора, но исходя из логики исследования, положим, что он
бесповторный. Поскольку выборка 5%-ная, то объем генеральной совокупности (общая посевная площадь области)
составляет:
гектаров – не знаю, насколько это
реалистично, оставим этот вопрос на совести автора задачи.
По условию, требуется найти предельную ошибку выборки (точность оценки) , где
–
коэффициент доверия, соответствующий доверительной вероятности , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле
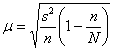
, который с вероятностью 99,74% (практически достоверно) накроет генеральную среднюю
урожайность
подсолнечника по области.
И если с коэффициентом «тэ гаммовое» трудностей никаких, то коэффициент «мю» здесь трудовой – по той причине, что нам не
известна исправленная выборочная дисперсия. Ну что же, хороший повод освежить пройденный материал. Смотрим на таблицу
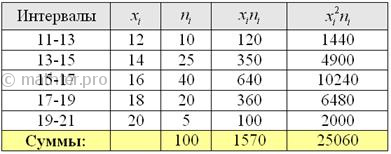
выше и приходим к выводу, что нам предложен интервальный вариационный ряд с
открытыми крайними интервалами. Поскольку длина частичного интервала составляет га, то вопрос закрываем так: 11-13 и 19-21 га.
Находим середины интервалов (переходим к
дискретному ряду), произведения и их суммы:
Вычислим выборочную среднюю: центнеров с гектара.
Выборочную дисперсию вычислим по формуле:
и этим частенько пренебрегают, но я
призываю поправлять дисперсию:
– мелочь, а приятно.
Теперь составляем доверительный интервал ,
где .
Найдём коэффициент доверия .
Поскольку нам известна лишь исправленная выборочная дисперсия (а не генеральная), то правильнее использовать распределение
Стьюдента. Но, к сожалению, в таблице нет значений для , но зато есть расчётный макет (пункт 2б). Для заданной надёжности и количества степеней свободы
получаем
.
Поскольку объём выборки , то можно использовать
нормальное распределение, и тут получается конфетка:
, какой способ выбрать – зависит от вашей
методички, и я так подозреваю, второй :). Но сейчас выберем первый.
Вычислим среднюю ошибку бесповторной выборки:
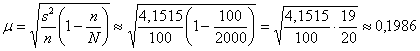
составляет ц/га, и искомый доверительный
интервал:
(ц/га) – границы, в которых ожидается
средняя урожайность подсолнечника в области с вероятностью (практически достоверно).
Ответ: ц/га,
(ц/га)
В рассмотренной задаче можно поставить вопросы, аналогичные Примеру 25, а именно попытаться улучшить исследование, в
частности, уменьшить точность оценки . В этом
случае для определения необходимого объема выборки используется та же формула 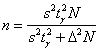
. Такие задачи, однако, встречаются, будьте
готовы. Да, и аналогичная формула для повторной выборки: .
Пример 28
По результатам 10%-ной бесповторной выборки объёма , найдены выборочная средняя
и дисперсия
.
а) Найти пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение генеральной совокупности.
б) Найти эти пределы, если выборка повторная. Какой способ точнее?
Значение 0,954 обусловлено тем, что автор задачи пощадил студентов, в методичке используется функция Лапласа и получается целое значение .
Решаем самостоятельно!


| Оглавление |
Загрузить PDF
Загрузить PDF
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента). Выполните следующие действия, чтобы вычислить доверительный интервал для нужных величин.
Шаги
-
1
Запишите задачу. Например: средний вес студента мужского пола в университете АВС составляет 90 кг. Вы будете тестировать точность предсказания веса студентов мужского пола в университете АВС в пределах данного доверительного интервала.
-
2
Составьте подходящую выборку. Вы будете использовать ее для сбора данных для тестирования гипотезы. Допустим, вы уже случайно выбрали 1000 студентов мужского пола.
-
3
Рассчитайте среднее значение и стандартное отклонение этой выборки. Выберите статистические величины (например, среднее значение и стандартное отклонение), которые вы хотите использовать для анализа вашей выборки. Вот как вычислить среднее значение и стандартное отклонение:
- Для расчета среднего значения выборки сложите значения весов 1000 выбранных мужчин и разделите результат на 1000 (число мужчин). Допустим, получили средний вес, равный 93 кг.
- Для расчета стандартного отклонения выборки необходимо найти среднее значение. Затем нужно вычислить дисперсию данных или среднее значение квадратов разностей от среднего. Найдя это число, просто возьмите квадратный корень из него. Допустим, в нашем примере стандартное отклонение равно 15 кг (заметим, что иногда эта информация может быть дана вместе с условием статистической задачи).
-
4
Выберите нужный доверительный уровень. Наиболее часто используемые доверительные уровни: 90 %, 95 % и 99 %. Он также может быть дан вместе с условием задачи. Допустим, вы выбрали 95 %.
-
5
Рассчитайте предел погрешности. Вы можете найти предел погрешности с помощью следующей формулы: Za/2 * σ/√(n). Za/2 = коэффициент доверия (где а = доверительный уровень), σ = стандартное отклонение, а n = размер выборки. Это формула показывает, что вы должны умножить критическое значение на стандартную ошибку. Вот как вы можете решить эту формулу, разбив ее на части:
- Вычислите критическое значение или Za/2. Доверительный уровень равен 95 %. Преобразуйте проценты в десятичную дробь: 0,95 и разделите ее на 2, чтобы получить 0,475. Затем посмотрите в таблицу Z-оценок, чтобы найти соответствующее значение для 0,475. Вы найдете значение 1,96 (на пересечении строки 1,9 и столбца 0,06).
- Возьмите стандартную ошибку (стандартное отклонение): 15 и разделите ее на квадратный корень из размера выборки: 1000. Вы получите: 15/31,6 или 0,47 кг.
- Умножьте 1,96 на 0,47 (критическое значение на стандартную ошибку), чтобы получить 0,92 — предел погрешности.
-
6
Запишите доверительный интервал. Чтобы сформулировать доверительный интервал, просто запишите среднее значение (93) ± погрешность. Ответ: 93 ± 0,92. Вы можете найти верхнюю и нижнюю границы доверительного интервала, прибавляя и вычитая погрешность к/от средней величины. Итак, нижняя граница составляет 93 — 0,92 или 92,08, а верхняя граница составляет 93 + 0,92 или 93,92.
- Вы можете использовать следующую формулу для вычисления доверительного интервала: x̅ ± Za/2 * σ/√(n), где x̅ — среднее значение.
Реклама
Советы
- И t-оценки и z-оценки можно рассчитать вручную, а также с помощью графического калькулятора или статистических таблиц, которые часто встречаются в учебниках по статистике. Также доступны онлайн-инструменты.
- Критическое значение, используемое для расчета погрешности, является постоянным и выражается либо через t-оценку, либо через z-оценку. T-оценка обычно более предпочтительна в условиях, когда стандартное отклонение выборки неизвестно или когда используется маленькая выборка.
- Ваша выборка должна быть достаточной (по размеру) для того, чтобы вычислить правильный доверительный интервал.
- Доверительный интервал не указывает на вероятность получения того или иного результата. Например, если вы на 95 % уверены, что среднее значение вашей выборки лежит между 75 и 100, то доверительный интервал в 95 % не означает, что среднее значение попадает в ваш диапазон.
- Есть много методов, таких как простая случайная выборка, систематический отбор и стратифицированная выборка, с помощью которых вы можете собрать репрезентативную выборку для тестирования.
Реклама
Что вам понадобится
- Выборка
- Компьютер
- Доступ в интернет
- Учебник статистики
- Графический калькулятор
Об этой статье
Эту страницу просматривали 264 469 раз.














 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп