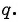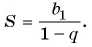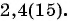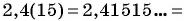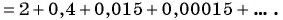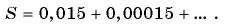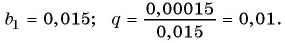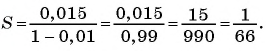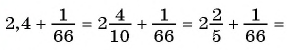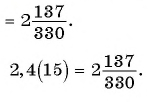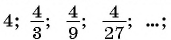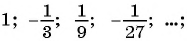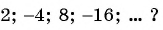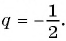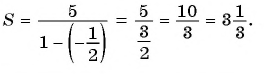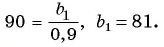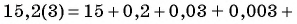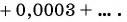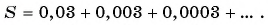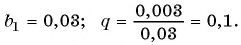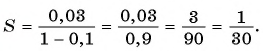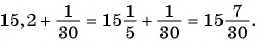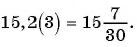У этого термина существуют и другие значения, см. w:Прогрессия.
Арифмети́ческая прогре́ссия (АП) — числовая последовательность вида
,
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа 
Любой (n — й) член прогрессии может быть вычислен по формуле общего члена:
Обозначение. Если последовательность 






Коротко: арифметическая прогрессия обозначается через 
Арифметическая прогрессия является монотонной последовательностью. При 



Свойства[править]
1. Общий член арифметической прогрессии[править]
Член арифметической прогрессии с номером 
- где
— первый член прогрессии,
— её разность,
— член арифметической прогрессии с номером
.
Доказательство: 
|
|---|
Пользуясь соотношением  выписываем последовательно несколько членов прогрессии: выписываем последовательно несколько членов прогрессии:
Заметив закономерность, делаем предположение, что База индукции
Переход индукции: Пусть наше утверждение верно при
Итак, утверждение верно и при |
Теперь перейдём к другому равенству.
Доказательство: 
|
|---|
Рассмотрим дважды предыдущую формулу для  -го и -го и  -го членов арифметической прогрессии. Имеем -го членов арифметической прогрессии. Имеем
Найдём их разность: |
Иногда удобно пользоваться формулой для члена арифметической прогрессии с 


Доказательство: 
|
|---|
Запишем формулу  Положим Положим  и и  Тогда Тогда
|
2. Разность арифметической прогрессии[править]
Из определения арифметической прогрессии имеем:
Ещё одна формула:
Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как
3. Признаки арифметической прогрессии[править]
На данный момент известны три критерия арифметической прогрессии. Вот они:
1. Последовательность 





| Доказательство |
|---|
Рассмотрим разность двух произвольных последовательных членов данной  . Имеем . Имеем
Следовательно, при любом |
2. Последовательность 

3. Последовательность 




P. S. Про остальные два критерия смотрите далее.
4. Характеристическое свойство арифметической прогрессии[править]
Последовательность 


| Доказательство |
|---|
| Необходимость:
Поскольку
Сложив эти равенства и разделив обе части на 2, получим Достаточность: Имеем, что для каждого элемента последовательности, начиная со второго, выполняется База индукции
Переход индукции: Пусть наше утверждение верно при
Но по предположению индукции следует, что Итак, утверждение верно и при Обозначим эти разности через |
Нетрудно сделать следующее предположение (обобщённое характеристическое свойство): 
| Доказательство |
|---|
Поскольку, очевидно, что для индекса  члена члена  выполняется двойное неравенство: выполняется двойное неравенство:  , то воспользуемся формулой разности к некоторой паре , то воспользуемся формулой разности к некоторой паре   , где , где  . .
Мы дважды воспользуемся ею для двух пар, то есть |
5. Лемма арифметической прогрессии[править]
Довольно любопытный факт можно заметить: 

Лемма. Суммы членов арифметической прогрессии с равными суммами номеров равны: если 


| Доказательство |
|---|
Пусть  . Рассмотрим левую часть требуемого равенства. Член . Рассмотрим левую часть требуемого равенства. Член  может быть представлен как может быть представлен как  . В свою очередь, ничто не мешает это повторить и для члена . В свою очередь, ничто не мешает это повторить и для члена  , то есть , то есть  . Тогда их сумма равна: . Тогда их сумма равна: ![{displaystyle a_{n}+a_{m}=[a_{1}+(n-1)d]+[a_{1}+(m-1)d]=2a_{1}+(n+m-2)d}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17ed4862b6cacd614eab35251e4bfe20545d286) . .
По условию |
Следствие 1. Последовательность 

Следствие 2. Лемму также можно представить в другой форме: 
| Доказательство |
|---|
| Достаточно проверить условие леммы. |
6. Тождество арифметической прогрессии[править]
Оказывается, что любые три члена арифметической прогрессии могут быть связаны между собой и своими индексами некоторым образом. Сформулируем данное утверждение.
6.1. Факт[править]
Пусть 





| Доказательство |
|---|
Решим следующую задачу.
Дано: Найти: Решение. Знаем, что В свою очередь, эта же разность
Поскольку левые части равны, то и правые подавно. Тогда верна такая запись:
Откуда по свойству пропорции имеем:
Итак, мы нашли, что хотели: Задача решена. В качестве следствия попутно нами доказано тождество арифметической прогрессии: |
6.2. Поучительный пример[править]
Дано: 


Решим эту задачу четырьмя способами, дабы показать их многообразие и эффективность.
Способ I [ через разность  ] ]
|
|---|
Находим сначала разность  по формуле по формуле 
И находим Ответ: |
Этот способ можно назвать «традиционный», поскольку опирается чисто на определения. А вот следующий зиждется на действительно интересном факте, о котором не все далеко знают, увы…
| Способ II [используя тождество] |
|---|
Знаем, что  можно вычислять по формуле можно вычислять по формуле 
Придадим переменным их значения и получим: Ответ: |
Всего одна формула дала нам нужный ответ! Безусловно, человеку хочется упростить всякие вычисления. В этом случае на помощь всегда приходит смекалка — посмотрите, как решить третьим способом.
| Способ III [по характеристическому свойству] |
|---|
| Итак, нам дана арифметическая прогрессия, поэтому выполняется обобщённое характеристическое свойство, а именно:
Придадим для этой формулы значения Выражаем Ответ: |
В некоторых случаях более внимательные всегда видят какие-нибудь закономерности. У нас именно такая ситуация, к нам на помощь приходит лемма!
| Способ IV [с помощью леммы] |
|---|
Так как  то можем применить лемму и записать: то можем применить лемму и записать:
Легко вычисляем нужный член
Ответ: |
7. Дополнительные формулы[править]
Можно без труда выводить ещё больше интересных формул. Приведём две из них и докажем первую, а вторая — по аналогии с отсылкой на первую.
- Формула 1:
| Доказательство |
|---|
Напишем сначала равенство  . .
Затем другое: Дальше просто: |
- Формула 2:
8. Сумма первых  членов арифметической прогрессии[править]
членов арифметической прогрессии[править]
- Сумма первых
членов арифметической прогрессии
может быть найдена по формулам:
| Доказательство |
|---|
| Запишем сумму двумя способами:
Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали:
(*) Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде
Получили, что каждое слагаемое не зависит от
Третья формула для суммы получается подстановкой Замечание: 1) Вместо (*) В доказательстве можно применить следствие 2 из леммы. |
Непосредственно из определения суммы первых 
Следствие 1. Член, стоящий на 

Более того, можно узреть и такой факт.
Следствие 2. Для любой пары 
| Доказательство |
|---|
Ясно, что  Аналогично с суммой Аналогично с суммой  , то есть , то есть  Вычтем первое равенство из второго: Вычтем первое равенство из второго:
|
Приоткроем ещё одну «тайну».
Следствие 3. Верна следующая формула при 

| Доказательство |
|---|
Методом математической индукцией по числу 
|
Следствие 4. Нетрудно вывести и такую формулу: 
| Доказательство |
|---|
По следствию 1 для  -го члена арифметической прогрессии можем написать следующее: -го члена арифметической прогрессии можем написать следующее:  Выразим Выразим  и получим: и получим:
|
Следствие 5. И наконец, вот ещё замечательная формула: 
Второй вариант записи: 
8.1. Сумма первых  чисел[править]
чисел[править]
Вопрос: как посчитать сумму от 


Например, сумма от 1 до 100 равна 
Если по известной сумме 



8.2. Сумма первых  нечётных чисел[править]
нечётных чисел[править]
Вопрос: какое будет 

Такое число должно быть: 


Поэтому сумма первых 
Например, 
Это свойство суммы нечётных чисел наглядно выражается чертежом , который составлен так: к квадрату (внизу слева) приставлены 3 таких же квадрата (1 сверху, 1 сбоку и 1 в верхнем углу); к этим квадратам приставлены ещё 5 квадратов (2 сверху, 2 сбоку и 1 в верхнем правом углу). К ним, далее, приложены 7 квадратов, потом 9 квадратов и т. д.
Тогда очевидно, что 
8.3. Интересный факт[править]
Формулировка: для всякой арифметической прогрессии при любом 
Примечание: 

| Доказательство |
|---|
Воспользуемся следствием 2 из пункта 8. Имеем  или или 
Прибавим к обеим частям Ну действительно, по тому же следствию 2 можно написать верное равенство:
Теперь докажем, что |
Комплементарное свойство суммы: 
9. Сумма членов арифметической прогрессии от  -ого до
-ого до  -ого[править]
-ого[править]
Сумма членов арифметической прогрессии с номерами от 


10. Сходимость арифметической прогрессии[править]
Арифметическая прогрессия 


| Доказательство |
|---|
Записав выражение для общего члена и исследуя предел  , получаем искомый результат. , получаем искомый результат.
|
11. Связь между арифметической и геометрической прогрессиями[править]
Пусть 




| Доказательство |
|---|
| Проверим характеристическое свойство для образованной геометрической прогрессии:
Воспользуемся выражением для общего члена арифметической прогрессии: Итак, поскольку характеристическое свойство выполняется, то |
Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.
Арифметические прогрессии высших порядков[править]
Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:
- 1, 4, 9, 16, 25, 36, …
разности которых образуют простую арифметическую прогрессию с разностью 2:
- 3, 5, 7, 9, 11, …
Треугольные числа 

Тетраэдральные числа 
Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.
Если ![{displaystyle left[a_{i}right]_{1}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d20714616bd224035f33bf8f7d3d80d5a18e82d9)




Примеры[править]
— первые 5 членов арифметической прогрессии, в которой
и
.
- Если все элементы некоторой последовательности равны между собой и равны некоторому числу
, то это есть арифметическая прогрессия, в которой
и
. В частности,
есть арифметическая прогрессия с разностью
.
- В физике — свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую. Какое расстояние пройдет тело за первую, вторую, третью,… секунду полета?
- В третьем тысячелетии високосными годами будут годы 2004, 2008,2012,…
- На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе через день, 2 дня, 3 дня,…?
- В литературе. Вспомним строки из романа А.С.Пушкина «Евгений Онегин», сказанные о его герое: «…Не мог он ямба от хорея, как мы ни бились, отличить». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Ямб — стихотворный метр с ударениями на четных слогах стиха: «Мой дядя самых честных правил…» (2, 4, 6, 8,…).
Хорей — стихотворный размер с ударением на нечетных слогах стиха: «Буря мглою небо кроет…» (1, 3, 5, 7,…)[5 стр.250].
Занимательная история[править]
Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050. Действительно, легко видеть, что решение сводится к формуле 

См. также[править]
- Геометрическая прогрессия
- Арифметико-геометрическая прогрессия
Ссылки[править]
- Шаблон:ВТ-ЭСБЕ
Примечания[править]
- ↑ Бронштейн, 1986, с. 139
Литература[править]
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся вузов. — М.: Наука, 1986. — 544 с.
Арифметическая прогрессия — коротко о главном
Определение арифметической прогрессии:
Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна ( displaystyle d).
Например:
- ( {{a}_{1}}=3)
- ( displaystyle {{a}_{2}}=3+d=7~Rightarrow d=7-3=4)
- ( displaystyle {{a}_{3}}=7+4=11) и т.д.
Арифметическая прогрессия бывает возрастающей (( displaystyle d>0)) и убывающей (( displaystyle d<0)).
Формула нахождения n-ого члена арифметической прогрессии:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) , где ( displaystyle n)– количество чисел в прогрессии.
Как найти член прогрессии, если известны его соседние члены:
( {{text{a}}_{text{n}}}=frac{{{text{a}}_{text{n}+1}}+{{text{a}}_{text{n}-1}}}{2}) — где ( displaystyle n) – количество чисел в прогрессии.
Сумма членов арифметической прогрессии:
1-й способ: ( {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.
2-й способ: ( displaystyle {{s}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.
Числовая последовательность
Итак, сядем и начнем писать какие-нибудь числа. Например: ( displaystyle 4,text{ }7,text{ }-8,text{ }13,text{ }-5,text{ }-6,text{ }0,text{ }ldots )
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ( displaystyle 7)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.
Это и есть пример числовой последовательности.
Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:
Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и ( displaystyle n)-ное число) всегда одно.
Число с номером ( displaystyle n) называется ( displaystyle n)-ным членом последовательности.
Всю последовательность мы обычно называем какой-нибудь буквой (например, ( displaystyle a)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: ( displaystyle {{a}_{1}},text{ }{{a}_{2}},text{ }…,text{ }{{a}_{10}},text{ }…,text{ }{{a}_{n}}).
Арифметическая прогрессия — определения
Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.
Например:
( begin{array}{l}{{a}_{1}}=3\{{a}_{2}}=3+d=7~~~Rightarrow ~d=7-3=4\{{a}_{3}}=7+4=11end{array})
Такая числовая последовательность называется арифметической прогрессией.
Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.
Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.
Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:
- ( displaystyle 3;text{ }6;text{ }9;text{ }12;text{ }15;text{ }17ldots )
- ( displaystyle 1;text{ }12;text{ }23;text{ }34;text{ }45text{ }ldots )
- ( displaystyle -5;text{ }-1;text{ }3;text{ }7;text{ }11;text{ }15ldots )
- ( displaystyle -6;text{ }5;text{ }17;text{ }28;text{ }39ldots )
Разобрался? Сравним наши ответы:
Является арифметической прогрессией – 2, 3.
Не является арифметической прогрессией – 1, 4.
Вернемся к заданной прогрессии (( displaystyle 3;text{ }7;text{ }11;text{ }15;text{ }19ldots )) и попробуем найти значение ее 6-го члена.
Существует два способа его нахождения.
Нахождения n-ого члена арифметической прогрессии
Способ I
Мы можем прибавлять к предыдущему значению числа прогрессии ( d=4) , пока не дойдем до ( displaystyle 6)-го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:
( begin{array}{l}{{a}_{4}}=11+4=15\{{a}_{5}}=15+4=19\{{a}_{6}}=19+4=23end{array})
Итак, 6-ой член описанной арифметической прогрессии равен 23.
Способ II
А что если нам нужно было бы найти значение ( displaystyle 140)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.
А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.
Это и есть математика!
Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка.
Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.
Что мы знаем?
- У нас есть арифметическая прогрессия: 3, 7, 11, 15, 19 и т.д.
- У нас есть номера прогрессии: 1, 2, 3, 4, 5, и т.д.
- Мы все время прибавляем 4, значит разница прогрессии d = 4.
Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.
7=3+4 или 7=3+d
Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?
11=3+4+4 или 11=3+d+d
Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.
Давай проверим? Чему равен 4-й член арифметической прогрессии?
15=3+4+4+4 или 15=3+d+d+d
Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!
Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа.
А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.
Например, посмотрим, из чего складывается значение ( displaystyle 4)-го члена данной арифметической прогрессии:
( begin{array}{l}{{a}_{4}}={{a}_{1}}+dleft( 4-1 right)\{{a}_{4}}=3+4left( 4-1 right)=15end{array})
Попробуй самостоятельно найти таким способом значение члена ( displaystyle n=6) данной арифметической прогрессии.
Рассчитал? Сравни свои записи с ответом:
( begin{array}{l}{{a}_{6}}={{a}_{1}}+dleft( 6-1 right)\{{a}_{6}}=3+4left( 6-1 right)=3+4cdot 5=3+20=23end{array})
Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли ( displaystyle d) к предыдущему значению членов арифметической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)) – уравнение арифметической прогрессии.
Кстати, таким образом мы можем посчитать и ( displaystyle 140)-ой член данной арифметической прогрессии (да и ( displaystyle 169)-ый тоже можем, да и любой другой вычислить совсем несложно).
Попробуй посчитать значения ( displaystyle 140)-го и ( displaystyle 169)-го членов, применив полученную формулу.
( begin{array}{l}…\{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=3+4left( 140-1 right)=3+4cdot 139=3+556=559\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=3+4left( 169-1 right)=3+4cdot 168=3+672=675end{array})
Возрастающие и убывающие арифметические прогрессии
Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.
Например:
( displaystyle begin{array}{l}4;text{ }6;text{ }8;text{ }10;text{ }12\-2;text{ }4;text{ }10;text{ }16;text{ }20end{array})
Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.
Например:
( displaystyle begin{array}{l}12;text{ }10;text{ }8;text{ }6;text{ }4\4;text{ }0;text{ }-4;text{ }-8;text{ }-12.end{array})
Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.
Проверим это на практике.
Нам дана арифметическая прогрессия, состоящая из следующих чисел: ( displaystyle 13;text{ }8;text{ }4;text{ }0;text{ }-4.)
Проверим, какое получится ( displaystyle 4)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:
( {{text{a}}_{text{n}}}={{text{a}}_{1}}+text{d}left( text{n}-1 right))
Заметим, что так как арифметическая прогрессия убывающая, то значение ( displaystyle d) будет отрицательным, ведь каждый последующий член меньше предыдущего.
( displaystyle d=8-13=-5)
( {{a}_{4}}={{a}_{1}}+dleft( 4-1 right))
Так как ( displaystyle d=-5), то:
( {{a}_{4}}=13-5left( 4-1 right)=13-15=-2)
Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.
Попробуй самостоятельно найти ( displaystyle 140)-ой и ( displaystyle 169)-ый члены этой арифметической прогрессии.
Сравним полученные результаты:
( begin{array}{l}{{a}_{140}}={{a}_{1}}+dleft( 140-1 right)\{{a}_{140}}=13-5left( 140-1 right)=13-5cdot 139=13-695=-682\{{a}_{169}}={{a}_{1}}+dleft( 169-1 right)\{{a}_{169}}=13-5left( 169-1 right)=13-5cdot 168=13-840=-827end{array})
Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)
Усложним задачу — выведем свойство арифметической прогрессии.
Допустим, нам дано такое условие:
( displaystyle 4;text{ }x;text{ }12ldots ) — арифметическая прогрессия, найти значение ( displaystyle x).
Легко, скажешь ты и начнешь считать по уже известной тебе формуле:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))
Пусть ( displaystyle {{a}_{1}}=4), а ( displaystyle {{a}_{3}}=12), тогда:
( displaystyle begin{array}{l}{{a}_{3}}={{a}_{1}}+dleft( 3-1 right)\12=4+2d~~Rightarrow ~d=frac{12-4}{2}=4\{{a}_{2}}=x={{a}_{1}}+d\{{a}_{2}}=x=4+4=8end{array})
Абсолютно верно.
Получается, мы сначала находим ( displaystyle d), потом прибавляем его к первому числу и получаем искомое ( displaystyle x).
Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа ( displaystyle 4024;~x;6072)?
Согласись, есть вероятность ошибиться в вычислениях.
А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?
Конечно да, и именно ее мы попробуем сейчас вывести.
Обозначим искомый член арифметической прогрессии как ( {{text{a}}_{text{n}}}), формула его нахождения нам известна – это та самая формула, выведенная нами в начале:
( {{a}_{n}}={{a}_{1}}+dleft( n-1 right)), тогда:
- предыдущий член прогрессии это ( {{a}_{n}}-d): ( {{a}_{n-1}}={{a}_{1}}+dleft( n-1 right)-d)
- последующий член прогрессии это ( {{a}_{n}}+d): ( {{a}_{n+1}}={{a}_{1}}+dleft( n-1 right)+d)
Просуммируем предыдущий и последующий члены прогрессии:
( {{a}_{1}}+dleft( n-1 right)-d+{{{a}}_{1}}+text{d}left( text{n}-1 right)+text{d}=2left( {{a}_{1}}+dleft( n-1 right) right)text{ }!!~!!text{ })
Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.
Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на ( 2).
( {{a}_{n}}=frac{{{a}_{n+1}}+{{a}_{n-1}}}{2}) – свойство членов арифметической прогрессии.
Попробуем посчитать значение ( x), используя выведенную формулу:
( x=frac{4+12}{2}=8)
Все верно, мы получили это же число. Закрепим материал.
Посчитай значение ( x) для прогрессии ( displaystyle 4024;~x;6072) самостоятельно, ведь это совсем несложно.
( x=frac{4024+6072}{2}=5048)
Молодец! Ты знаешь о прогрессии почти все!
Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…
Сумма первых n членов арифметической прогрессии
Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:
«Сосчитать сумму всех натуральных чисел от ( displaystyle 1) до ( displaystyle 40) (по другим источникам до ( displaystyle 100)) включительно».
Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…
Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.
Допустим, у нас есть арифметическая прогрессия, состоящая из ( displaystyle 6)-ти членов: ( displaystyle 6;text{ }8;text{ }10;text{ }12;text{ }14;text{ }16…)
Нам необходимо найти сумму данных ( displaystyle 6) членов арифметической прогрессии.
Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму ( displaystyle 100) ее членов, как это искал Гаусс?
Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.
Попробовал? Что ты заметил? Правильно! Их суммы равны
А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?
Конечно, ровно половина всех чисел, то есть ( frac{6}{2}=3).
Исходя из того, что сумма двух членов арифметической прогрессии равна ( 22), а подобных равных пар ( 3), мы получаем, что общая сумма равна:
( displaystyle Stext{ }=text{ }22cdot 3text{ }=text{ }66).
Таким образом, формула для суммы первых ( displaystyle n) членов любой арифметической прогрессии будет такой:
( displaystyle {{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}), где ( displaystyle n) – количество значений.
В некоторых задачах нам неизвестен ( displaystyle n)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу ( displaystyle n)-го члена. ( {{a}_{n}}={{a}_{1}}+dleft( n-1 right))
Что у тебя получилось?
( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n), где ( displaystyle n) – количество значений.
Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма ( displaystyle 40) чисел, начиная от ( displaystyle 1)-го, и сумма ( displaystyle 100) чисел начиная от ( displaystyle 1)-го.
Сколько у тебя получилось?
У Гаусса получилось, что сумма ( displaystyle 100 ) членов равна ( displaystyle 5050), а сумма ( displaystyle 40 ) членов ( displaystyle 820).
Так ли ты решал?
- ( {{S}_{40}}=frac{left( 1+40 right)cdot 40}{2}=frac{41cdot 40}{2}=frac{1640}{2}=820)
- ( {{S}_{100}}=frac{left( 1+100 right)cdot 100}{2}=frac{101cdot 100}{2}=5050)
На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.
Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.
Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется ( displaystyle 6) блочных кирпичей.
Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?
В данном случае прогрессия выглядит следующим образом:
( displaystyle 6;text{ }5;text{ }4;text{ }3;text{ }2; 1).
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Способ 1.
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\~~{{S}_{6}}=frac{left( 6+1 right)cdot 6}{2}=frac{7cdot 6}{2}=21\~end{array})
Способ 2.
( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n)
( {{S}_{n}}=frac{2cdot 6+1left( 6-1 right)}{2}cdot 6=frac{12+5cdot 6}{2}=frac{7cdot 6}{2}=frac{42}{2}=21)
А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.
Сошлось?
Молодец, ты освоил сумму ( displaystyle n)-ных членов арифметической прогрессии.
Конечно, из ( displaystyle 6) блоков в основании пирамиду не построишь, а вот из ( displaystyle 60)?
Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – ( displaystyle 1830) блоков:
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\{{S}_{60}}=frac{left( 60+1 right)cdot 60}{2}=frac{61cdot 60}{2}=61cdot 30=1830.end{array})
Арифметическая прогрессия: что это такое?
5 января 2017
- Тренировочные задачи
- Ответы и решения

Что ж, друзья, если вы читаете этот текст, то внутренний кэп-очевидность подсказывает мне, что вы пока ещё не знаете, что такое арифметическая прогрессия, но очень (нет, вот так: ОООООЧЕНЬ!) хотите узнать. Поэтому не буду мучать вас длинными вступлениями и сразу перейду к делу.
Для начала парочка примеров. Рассмотрим несколько наборов чисел:
- 1; 2; 3; 4; …
- 15; 20; 25; 30; …
- $sqrt{2}; 2sqrt{2}; 3sqrt{2};…$
Что общего у всех этих наборов? На первый взгляд — ничего. Но на самом деле кое-что есть. А именно: каждый следующий элемент отличается от предыдущего на одно и то же число.
Судите сами. Первый набор — это просто идущие подряд числа, каждое следующее на единицу больше предыдущего. Во втором случае разница между рядом стоящими числами уже равна пяти, но эта разница всё равно постоянна. В третьем случае вообще корни. Однако $2sqrt{2}=sqrt{2}+sqrt{2}$, а $3sqrt{2}=2sqrt{2}+sqrt{2}$, т.е. и в этом случае каждый следующий элемент просто возрастает на $sqrt{2}$ (и пусть вас не пугает, что это число — иррациональное).
Так вот: все такие последовательности как раз и называются арифметическими прогрессиями. Дадим строгое определение:
Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией. Сама величина, на которую отличаются числа, называется разностью прогрессии и чаще всего обозначается буквой $d$.
Обозначение: $left( {{a}_{n}} right)$ — сама прогрессия, $d$ — её разность.
И сразу парочка важных замечаний. Во-первых, прогрессией считается лишь упорядоченная последовательность чисел: их разрешено читать строго в том порядке, в котором они записаны — и никак иначе. Переставлять и менять местами числа нельзя.
Во-вторых, сама последовательность может являться как конечной, так и бесконечной. К примеру, набор {1; 2; 3} — это, очевидно, конечная арифметическая прогрессия. Но если записать что-нибудь в духе {1; 2; 3; 4; …} — это уже бесконечная прогрессия. Многоточие после четвёрки как бы намекает, что дальше идёт ещё довольно много чисел. Бесконечно много, например.:)
Ещё хотел бы отметить, что прогрессии бывают возрастающими и убывающими. Возрастающие мы уже видели — тот же набор {1; 2; 3; 4; …}. А вот примеры убывающих прогрессий:
- 49; 41; 33; 25; 17; …
- 17,5; 12; 6,5; 1; −4,5; −10; …
- $sqrt{5}; sqrt{5}-1; sqrt{5}-2; sqrt{5}-3;…$
Ладно, ладно: последний пример может показаться чересчур сложным. Но остальные, думаю, вам понятны. Поэтому введём новые определения:
Определение. Арифметическая прогрессия называется:
- возрастающей, если каждый следующий элемент больше предыдущего;
- убывающей, если, напротив, каждый последующий элемент меньше предыдущего.
Кроме того, существуют так называемые «стационарные» последовательности — они состоят из одного и того же повторяющегося числа. Например, {3; 3; 3; …}.
Остаётся лишь один вопрос: как отличить возрастающую прогрессию от убывающей? К счастью, тут всё зависит лишь от того, каков знак числа $d$, т.е. разности прогрессии:
- Если $d gt 0$, то прогрессия возрастает;
- Если $d lt 0$, то прогрессия, очевидно, убывает;
- Наконец, есть случай $d=0$ — в этом случае вся прогрессия сводится к стационарной последовательности одинаковых чисел: {1; 1; 1; 1; …} и т.д.
Попробуем рассчитать разность $d$ для трёх убывающих прогрессий, приведённых выше. Для этого достаточно взять любые два соседних элемента (например, первый и второй) и вычесть из числа, стоящего справа, число, стоящее слева. Выглядеть это будет вот так:
- 41−49=−8;
- 12−17,5=−5,5;
- $sqrt{5}-1-sqrt{5}=-1$.
Как видим, во всех трёх случаях разность действительно получилась отрицательной. И теперь, когда мы более-менее разобрались с определениями, пора разобраться с тем, как описываются прогрессии и какие у них свойства.
Члены прогрессии и рекуррентная формула
Поскольку элементы наших последовательностей нельзя менять местами, их можно пронумеровать:
[left( {{a}_{n}} right)=left{ {{a}_{1}}, {{a}_{2}},{{a}_{3}},… right}]
Отдельные элементы этого набора называются членами прогрессии. На них так и указывают с помощью номера: первый член, второй член и т.д.
Кроме того, как мы уже знаем, соседние члены прогрессии связаны формулой:
[{{a}_{n}}-{{a}_{n-1}}=dRightarrow {{a}_{n}}={{a}_{n-1}}+d]
Короче говоря, чтобы найти $n$-й член прогрессии, нужно знать $n-1$-й член и разность $d$. Такая формула называется рекуррентной, поскольку с её помощью можно найти любое число, лишь зная предыдущее (а по факту — все предыдущие). Это очень неудобно, поэтому существует более хитрая формула, которая сводит любые вычисления к первому члену и разности:
[{{a}_{n}}={{a}_{1}}+left( n-1 right)d]
Наверняка вы уже встречались с этой формулой. Её любят давать во всяких справочниках и решебниках. Да и в любом толковом учебнике по математике она идёт одной из первых.
Тем не менее предлагаю немного потренироваться.
Задача №1. Выпишите первые три члена арифметической прогрессии $left( {{a}_{n}} right)$, если ${{a}_{1}}=8,d=-5$.
Решение. Итак, нам известен первый член ${{a}_{1}}=8$ и разность прогрессии $d=-5$. Воспользуемся только что приведённой формулой и подставим $n=1$, $n=2$ и $n=3$:
[begin{align} & {{a}_{n}}={{a}_{1}}+left( n-1 right)d; \ & {{a}_{1}}={{a}_{1}}+left( 1-1 right)d={{a}_{1}}=8; \ & {{a}_{2}}={{a}_{1}}+left( 2-1 right)d={{a}_{1}}+d=8-5=3; \ & {{a}_{3}}={{a}_{1}}+left( 3-1 right)d={{a}_{1}}+2d=8-10=-2. \ end{align}]
Ответ: {8; 3; −2}
Вот и всё! Обратите внимание: наша прогрессия — убывающая.
Конечно, $n=1$ можно было и не подставлять — первый член нам и так известен. Впрочем, подставив единицу, мы убедились, что даже для первого члена наша формула работает. В остальных случаях всё свелось к банальной арифметике.
Задача №2. Выпишите первые три члена арифметической прогрессии, если её седьмой член равен −40, а семнадцатый член равен −50.
Решение. Запишем условие задачи в привычных терминах:
[{{a}_{7}}=-40;quad {{a}_{17}}=-50.]
Далее распишем 7-й и 17-й члены через формулу $n$-го члена прогрессии:
[left{ begin{align} & {{a}_{7}}={{a}_{1}}+6d \ & {{a}_{17}}={{a}_{1}}+16d \ end{align} right.]
[left{ begin{align} & {{a}_{1}}+6d=-40 \ & {{a}_{1}}+16d=-50 \ end{align} right.]
Знак системы я поставил потому, что эти требования должны выполняться одновременно. А теперь заметим, если вычесть из второго уравнения первое (мы имеем право это сделать, т.к. у нас система), то получим вот что:
[begin{align} & {{a}_{1}}+16d-left( {{a}_{1}}+6d right)=-50-left( -40 right); \ & {{a}_{1}}+16d-{{a}_{1}}-6d=-50+40; \ & 10d=-10; \ & d=-1. \ end{align}]
Вот так просто мы нашли разность прогрессии! Осталось подставить найденное число в любое из уравнений системы. Например, в первое:
[begin{matrix} {{a}_{1}}+6d=-40;quad d=-1 \ Downarrow \ {{a}_{1}}-6=-40; \ {{a}_{1}}=-40+6=-34. \ end{matrix}]
Теперь, зная первый член и разность, осталось найти второй и третий член:
[begin{align} & {{a}_{2}}={{a}_{1}}+d=-34-1=-35; \ & {{a}_{3}}={{a}_{1}}+2d=-34-2=-36. \ end{align}]
Готово! Задача решена.
Ответ: {−34; −35; −36}
Обратите внимание на любопытное свойство прогрессии, которое мы обнаружили: если взять $n$-й и $m$-й члены и вычесть их друг из друга, то мы получим разность прогрессии, умноженную на число $n-m$:
[{{a}_{n}}-{{a}_{m}}=dcdot left( n-m right)]
Простое, но очень полезное свойство, которое обязательно надо знать — с его помощью можно значительно ускорить решение многих задач по прогрессиям. Вот яркий тому пример:
Задача №3. Пятый член арифметической прогрессии равен 8,4, а её десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.
Решение. Поскольку ${{a}_{5}}=8,4$, ${{a}_{10}}=14,4$, а нужно найти ${{a}_{15}}$, то заметим следующее:
[begin{align} & {{a}_{15}}-{{a}_{10}}=5d; \ & {{a}_{10}}-{{a}_{5}}=5d. \ end{align}]
Но по условию ${{a}_{10}}-{{a}_{5}}=14,4-8,4=6$, поэтому $5d=6$, откуда имеем:
[begin{align} & {{a}_{15}}-14,4=6; \ & {{a}_{15}}=6+14,4=20,4. \ end{align}]
Ответ: 20,4
Вот и всё! Нам не потребовалось составлять какие-то системы уравнений и считать первый член и разность — всё решилось буквально в пару строчек.
Теперь рассмотрим другой вид задач — на поиск отрицательных и положительных членов прогрессии. Не секрет, что если прогрессия возрастает, при этом первый член у неё отрицательный, то рано или поздно в ней появятся положительные члены. И напротив: члены убывающей прогрессии рано или поздно станут отрицательными.
При этом далеко не всегда можно нащупать этот момент «в лоб», последовательно перебирая элементы. Зачастую задачи составлены так, что без знания формул вычисления заняли бы несколько листов — мы просто уснули бы, пока нашли ответ. Поэтому попробуем решить эти задачи более быстрым способом.
Задача №4. Сколько отрицательных членов в арифметической прогрессии −38,5; −35,8; …?
Решение. Итак, ${{a}_{1}}=-38,5$, ${{a}_{2}}=-35,8$, откуда сразу находим разность:
[d={{a}_{2}}-{{a}_{1}}=-35,8-left( -38,5 right)=38,5-35,8=2,7]
Заметим, что разность положительна, поэтому прогрессия возрастает. Первый член отрицателен, поэтому действительно в какой-то момент мы наткнёмся на положительные числа. Вопрос лишь в том, когда это произойдёт.
Попробуем выяснить: до каких пор (т.е. до какого натурального числа $n$) сохраняется отрицательность членов:
[begin{align} & {{a}_{n}} lt 0Rightarrow {{a}_{1}}+left( n-1 right)d lt 0; \ & -38,5+left( n-1 right)cdot 2,7 lt 0;quad left| cdot 10 right. \ & -385+27cdot left( n-1 right) lt 0; \ & -385+27n-27 lt 0; \ & 27n lt 412; \ & n lt 15frac{7}{27}Rightarrow {{n}_{max }}=15. \ end{align}]
Ответ: 15
Последняя строчка требует пояснения. Итак, нам известно, что $n lt 15frac{7}{27}$. С другой стороны, нас устроят лишь целые значения номера (более того: $nin mathbb{N}$), поэтому наибольший допустимый номер — это именно $n=15$, а ни в коем случае не 16.
Задача №5. В арифметической прогрессии ${{}_{5}}=-150,{{}_{6}}=-147$. Найдите номер первого положительного члена этой прогрессии.
Это была бы точь-в-точь такая же задача, как и предыдущая, однако нам неизвестно ${{a}_{1}}$. Зато известны соседние члены: ${{a}_{5}}$ и ${{a}_{6}}$, поэтому мы легко найдём разность прогрессии:
[d={{a}_{6}}-{{a}_{5}}=-147-left( -150 right)=150-147=3]
Кроме того, попробуем выразить пятый член через первый и разность по стандартной формуле:
[begin{align} & {{a}_{n}}={{a}_{1}}+left( n-1 right)cdot d; \ & {{a}_{5}}={{a}_{1}}+4d; \ & -150={{a}_{1}}+4cdot 3; \ & {{a}_{1}}=-150-12=-162. \ end{align}]
Теперь поступаем по аналогии с предыдущей задачей. Выясняем, в какой момент в нашей последовательности возникнут положительные числа:
[begin{align} & {{a}_{n}}=-162+left( n-1 right)cdot 3 gt 0; \ & -162+3n-3 gt 0; \ & 3n gt 165; \ & n gt 55Rightarrow {{n}_{min }}=56. \ end{align}]
Минимальное целочисленное решение данного неравенства — число 56.
Ответ: 56
Обратите внимание: в последнем задании всё свелось к строгому неравенству, поэтому вариант $n=55$ нас не устроит.
Теперь, когда мы научились решать простые задачи, перейдём к более сложным. Но для начала давайте изучим ещё одно очень полезное свойство арифметических прогрессий, которое в будущем сэкономит нам кучу времени и неравных клеток.:)
Среднее арифметическое и равные отступы
Рассмотрим несколько последовательных членов возрастающей арифметической прогрессии $left( {{a}_{n}} right)$. Попробуем отметить их на числовой прямой:
Я специально отметил произвольные члены ${{a}_{n-3}},…,{{a}_{n+3}}$, а не какие-нибудь ${{a}_{1}}, {{a}_{2}}, {{a}_{3}}$ и т.д. Потому что правило, о котором я сейчас расскажу, одинаково работает для любых «отрезков».
А правило очень простое. Давайте вспомним рекуррентную формулу и запишем её для всех отмеченных членов:
[begin{align} & {{a}_{n-2}}={{a}_{n-3}}+d; \ & {{a}_{n-1}}={{a}_{n-2}}+d; \ & {{a}_{n}}={{a}_{n-1}}+d; \ & {{a}_{n+1}}={{a}_{n}}+d; \ & {{a}_{n+2}}={{a}_{n+1}}+d; \ end{align}]
Однако эти равенства можно переписать иначе:
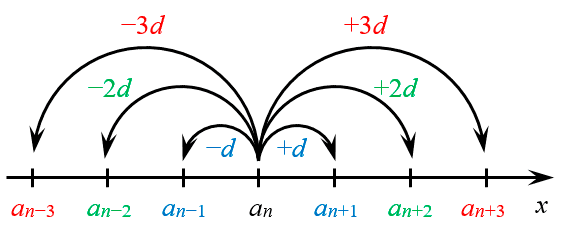
[begin{align} & {{a}_{n-1}}={{a}_{n}}-d; \ & {{a}_{n-2}}={{a}_{n}}-2d; \ & {{a}_{n-3}}={{a}_{n}}-3d; \ & {{a}_{n+1}}={{a}_{n}}+d; \ & {{a}_{n+2}}={{a}_{n}}+2d; \ & {{a}_{n+3}}={{a}_{n}}+3d; \ end{align}]
Ну и что с того? А то, что члены ${{a}_{n-1}}$ и ${{a}_{n+1}}$ лежат на одном и том же расстоянии от ${{a}_{n}}$. И это расстояние равно $d$. То же самое можно сказать про члены ${{a}_{n-2}}$ и ${{a}_{n+2}}$ — они тоже удалены от ${{a}_{n}}$ на одинаковое расстояние, равное $2d$. Продолжать можно до бесконечности, но смысл хорошо иллюстрирует картинка
Что это значит для нас? Это значит, что можно найти ${{a}_{n}}$, если известны числа-соседи:
[{{a}_{n}}=frac{{{a}_{n-1}}+{{a}_{n+1}}}{2}]
Мы вывели великолепное утверждение: всякий член арифметической прогрессии равен среднему арифметическому соседних членов! Более того: мы можем отступить от нашего ${{a}_{n}}$ влево и вправо не на один шаг, а на $k$ шагов — и всё равно формула будет верна:
[{{a}_{n}}=frac{{{a}_{n-k}}+{{a}_{n+k}}}{2}]
Т.е. мы спокойно можем найти какое-нибудь ${{a}_{150}}$, если знаем ${{a}_{100}}$ и ${{a}_{200}}$, потому что ${{a}_{150}}=frac{{{a}_{100}}+{{a}_{200}}}{2}$. На первый взгляд может показаться, что данный факт не даёт нам ничего полезного. Однако на практике многие задачи специально «заточены» под использование среднего арифметического. Взгляните:
Задача №6. Найдите все значения $x$, при которых числа $-6{{x}^{2}}$, $x+1$ и $14+4{{x}^{2}}$ являются последовательными членами арифметической прогрессии (в указанном порядке).
Решение. Поскольку указанные числа являются членами прогрессии, для них выполняется условие среднего арифметического: центральный элемент $x+1$ можно выразить через соседние элементы:
[begin{align} & x+1=frac{-6{{x}^{2}}+14+4{{x}^{2}}}{2}; \ & x+1=frac{14-2{{x}^{2}}}{2}; \ & x+1=7-{{x}^{2}}; \ & {{x}^{2}}+x-6=0. \ end{align}]
Получилось классическое квадратное уравнение. Его корни: $x=2$ и $x=-3$ — это и есть ответы.
Ответ: −3; 2.
Задача №7. Найдите значения $$, при которых числа $-1;4-3;{{}^{2}}+1$ составляют арифметическую прогрессию (в указанном порядке).
Решение. Опять выразим средний член через среднее арифметическое соседних членов:
[begin{align} & 4x-3=frac{x-1+{{x}^{2}}+1}{2}; \ & 4x-3=frac{{{x}^{2}}+x}{2};quad left| cdot 2 right.; \ & 8x-6={{x}^{2}}+x; \ & {{x}^{2}}-7x+6=0. \ end{align}]
Снова квадратное уравнение. И снова два корня: $x=6$ и$x=1$.
Ответ: 1; 6.
Если в процессе решения задачи у вас вылезают какие-то зверские числа, либо вы не до конца уверены в правильности найденных ответов, то есть замечательный приём, позволяющий проверить: правильно ли мы решили задачу?
Допустим, в задаче №6 мы получили ответы −3 и 2. Как проверить, что эти ответы верны? Давайте просто подставим их в исходное условие и посмотрим, что получится. Напомню, что у нас есть три числа ($-6{{}^{2}}$, $+1$ и $14+4{{}^{2}}$), которые должны составлять арифметическую прогрессию. Подставим $x=-3$:
[begin{align} & x=-3Rightarrow \ & -6{{x}^{2}}=-54; \ & x+1=-2; \ & 14+4{{x}^{2}}=50. end{align}]
Получили числа −54; −2; 50, которые отличаются на 52 — несомненно, это арифметическая прогрессия. То же самое происходит и при $x=2$:
[begin{align} & x=2Rightarrow \ & -6{{x}^{2}}=-24; \ & x+1=3; \ & 14+4{{x}^{2}}=30. end{align}]
Опять прогрессия, но с разностью 27. Таким образом, задача решена верно. Желающие могут проверить вторую задачу самостоятельно, но сразу скажу: там тоже всё верно.
В целом, решая последние задачи, мы наткнулись на ещё один интересный факт, который тоже необходимо запомнить:
Если три числа таковы, что второе является средним арифметическим первого и последнего, то эти числа образуют арифметическую прогрессию.
В будущем понимание этого утверждения позволит нам буквально «конструировать» нужные прогрессии, опираясь на условие задачи. Но прежде чем мы займёмся подобным «конструированием», следует обратить внимание на ещё один факт, который прямо следует из уже рассмотренного.
Группировка и сумма элементов
Давайте ещё раз вернёмся к числовой оси. Отметим там несколько членов прогрессии, между которыми, возможно. стоит очень много других членов:
Попробуем выразить «левый хвост» через ${{a}_{n}}$ и $d$, а «правый хвост» через ${{a}_{k}}$ и $d$. Это очень просто:
[begin{align} & {{a}_{n+1}}={{a}_{n}}+d; \ & {{a}_{n+2}}={{a}_{n}}+2d; \ & {{a}_{k-1}}={{a}_{k}}-d; \ & {{a}_{k-2}}={{a}_{k}}-2d. \ end{align}]
А теперь заметим, что равны следующие суммы:
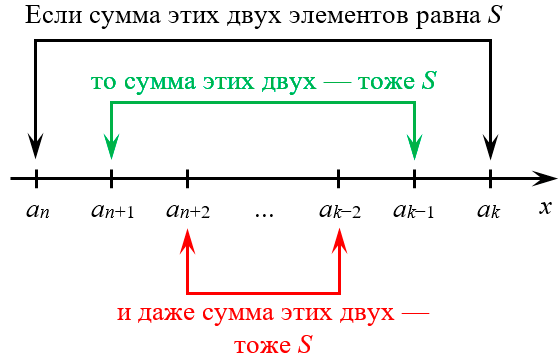
[begin{align} & {{a}_{n}}+{{a}_{k}}=S; \ & {{a}_{n+1}}+{{a}_{k-1}}={{a}_{n}}+d+{{a}_{k}}-d=S; \ & {{a}_{n+2}}+{{a}_{k-2}}={{a}_{n}}+2d+{{a}_{k}}-2d=S. end{align}]
Проще говоря, если мы рассмотрим в качестве старта два элемента прогрессии, которые в сумме равны какому-нибудь числу $S$, а затем начнём шагать от этих элементов в противоположные стороны (навстречу друг другу или наоборот на удаление), то суммы элементов, на которые мы будем натыкаться, тоже будут равны $S$. Наиболее наглядно это можно представить графически:
Понимание данного факта позволит нам решать задачи принципиально более высокого уровня сложности, нежели те, что мы рассматривали выше. Например, такие:
Задача №8. Определите разность арифметической прогрессии, в которой первый член равен 66, а произведение второго и двенадцатого членов является наименьшим из возможных.
Решение. Запишем всё, что нам известно:
[begin{align} & {{a}_{1}}=66; \ & d=? \ & {{a}_{2}}cdot {{a}_{12}}=min . end{align}]
Итак, нам неизвестна разность прогрессии $d$. Собственно, вокруг разности и будет строиться всё решение, поскольку произведение ${{a}_{2}}cdot {{a}_{12}}$ можно переписать следующим образом:
[begin{align} & {{a}_{2}}={{a}_{1}}+d=66+d; \ & {{a}_{12}}={{a}_{1}}+11d=66+11d; \ & {{a}_{2}}cdot {{a}_{12}}=left( 66+d right)cdot left( 66+11d right)= \ & =11cdot left( d+66 right)cdot left( d+6 right). end{align}]
Для тех, кто в танке: я вынес общий множитель 11 из второй скобки. Таким образом, искомое произведение представляет собой квадратичную функцию относительно переменной $d$. Поэтому рассмотрим функцию $fleft( d right)=11left( d+66 right)left( d+6 right)$ — её графиком будет парабола ветвями вверх, т.к. если раскрыть скобки, то мы получим:
[begin{align} & fleft( d right)=11left( {{d}^{2}}+66d+6d+66cdot 6 right)= \ & =11{{d}^{2}}+11cdot 72d+11cdot 66cdot 6 end{align}]
Как видим, коэффициент при старшем слагаемом равен 11 — это положительное число, поэтому действительно имеем дело с параболой ветвями вверх:
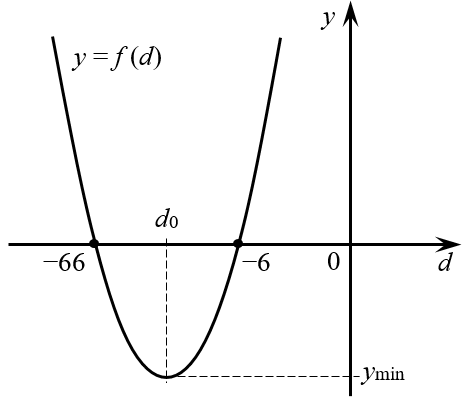
график квадратичной функции — парабола Обратите внимание: минимальное значение эта парабола принимает в своей вершине с абсциссой ${{d}_{0}}$. Конечно, мы можем посчитать эту абсциссу по стандартной схеме (есть же формула ${{d}_{0}}={-b}/{2a};$), но куда разумнее будет заметить, что искомая вершина лежит на оси симметрии параболы, поэтому точка ${{d}_{0}}$ равноудалена от корней уравнения $fleft( d right)=0$:
[begin{align} & fleft( d right)=0; \ & 11cdot left( d+66 right)cdot left( d+6 right)=0; \ & {{d}_{1}}=-66;quad {{d}_{2}}=-6. \ end{align}]
Именно поэтому я не особо спешил раскрывать скобки: в исходном виде корни было найти очень и очень просто. Следовательно, абсцисса равна среднему арифметическому чисел −66 и −6:
[{{d}_{0}}=frac{-66-6}{2}=-36]
Что даёт нам обнаруженное число? При нём требуемое произведение принимает наименьшее значение (мы, кстати, так и не посчитали ${{y}_{min }}$ — от нас это не требуется). Одновременно это число является разностью исходной прогрессии, т.е. мы нашли ответ.:)
Ответ: −36
Задача №9. Между числами $-frac{1}{2}$ и $-frac{1}{6}$ вставьте три числа так, чтобы они вместе с данными числами составили арифметическую прогрессию.
Решение. По сути, нам нужно составить последовательность из пяти чисел, причём первое и последнее число уже известно. Обозначим недостающие числа переменными $x$, $y$ и $z$:
[left( {{a}_{n}} right)=left{ -frac{1}{2};x;y;z;-frac{1}{6} right}]
Отметим, что число $y$ является «серединой» нашей последовательности — оно равноудалено и от чисел $x$ и $z$, и от чисел $-frac{1}{2}$ и $-frac{1}{6}$. И если из чисел $x$ и $z$ мы в данный момент не можем получить $y$, то вот с концами прогрессии дело обстоит иначе. Вспоминаем про среднее арифметическое:
[y=frac{-frac{1}{2}-frac{1}{6}}{2}=-frac{4}{2cdot 6}=-frac{1}{3}]
Теперь, зная $y$, мы найдём оставшиеся числа. Заметим, что $x$ лежит между числами $-frac{1}{2}$ и только что найденным $y=-frac{1}{3}$. Поэтому
[x=frac{-frac{1}{2}-frac{1}{3}}{2}=-frac{5}{6cdot 2}=-frac{5}{12}]
Аналогично рассуждая, находим оставшееся число:
[z=frac{-frac{1}{3}-frac{1}{6}}{2}=-frac{3}{6cdot 2}=-frac{1}{4}]
Готово! Мы нашли все три числа. Запишем их в ответе в том порядке, в котором они должны быть вставлены между исходными числами.
Ответ: $-frac{5}{12}; -frac{1}{3}; -frac{1}{4}$
Задача №10. Между числами 2 и 42 вставьте несколько чисел, которые вместе с данными числами образуют арифметическую прогрессию, если известно, что сумма первого, второго и последнего из вставленных чисел равна 56.
Решение. Ещё более сложная задача, которая, однако, решается по той же схеме, что и предыдущие — через среднее арифметическое. Проблема в том, что нам неизвестно, сколько конкретно чисел надо вставить. Поэтому положим для опредлённости, что после вставки всего будет ровно $n$ чисел, причём первое из них — это 2, а последнее — 42. В этом случае искомая арифметическая прогрессия представима в виде:
[left( {{a}_{n}} right)=left{ 2;{{a}_{2}};{{a}_{3}};…;{{a}_{n-1}};42 right}]
Далее распишем сумму первого, второго и последнего из вставленных чисел:
[{{a}_{2}}+{{a}_{3}}+{{a}_{n-1}}=56]
Заметим, однако, что числа ${{a}_{2}}$ и ${{a}_{n-1}}$ получаются из стоящих по краям чисел 2 и 42 путём одного шага навстречу друг другу, т.е. к центру последовательности. А это значит, что
[{{a}_{2}}+{{a}_{n-1}}=2+42=44]
Но тогда записанное выше выражение можно переписать так:
[begin{align} & {{a}_{2}}+{{a}_{3}}+{{a}_{n-1}}=56; \ & left( {{a}_{2}}+{{a}_{n-1}} right)+{{a}_{3}}=56; \ & 44+{{a}_{3}}=56; \ & {{a}_{3}}=56-44=12. \ end{align}]
Зная ${{a}_{3}}$ и ${{a}_{1}}$, мы легко найдём разность прогрессии:
[begin{align} & {{a}_{3}}-{{a}_{1}}=12-2=10; \ & {{a}_{3}}-{{a}_{1}}=left( 3-1 right)cdot d=2d; \ & 2d=10Rightarrow d=5. \ end{align}]
Осталось лишь найти остальные члены:
[begin{align} & {{a}_{1}}=2; \ & {{a}_{2}}=2+5=7; \ & {{a}_{3}}=12; \ & {{a}_{4}}=2+3cdot 5=17; \ & {{a}_{5}}=2+4cdot 5=22; \ & {{a}_{6}}=2+5cdot 5=27; \ & {{a}_{7}}=2+6cdot 5=32; \ & {{a}_{8}}=2+7cdot 5=37; \ & {{a}_{9}}=2+8cdot 5=42; \ end{align}]
Таким образом, уже на 9-м шаге мы придём в левый конец последовательности — число 42. Итого нужно было вставить лишь 7 чисел: 7; 12; 17; 22; 27; 32; 37.
Ответ: 7; 12; 17; 22; 27; 32; 37
Текстовые задачи с прогрессиями
В заключение хотелось бы рассмотреть парочку относительно простых задач. Ну, как простых: для большинства учеников, которые изучают математику в школе и не читали того, что написано выше, эти задачи могут показаться жестью. Тем не менее именно такие задачи попадаются в ОГЭ и ЕГЭ по математике, поэтому рекомендую ознакомиться с ними.
Задача №11. Бригада изготовила в январе 62 детали, а в каждый следующий месяц изготовляла на 14 деталей больше, чем в предыдущий. Сколько деталей изготовила бригада в ноябре?
Решение. Очевидно, количество деталей, расписанное по месяцам, будет представлять собой возрастающую арифметическую прогрессию. Причём:
[begin{align} & {{a}_{1}}=62;quad d=14; \ & {{a}_{n}}=62+left( n-1 right)cdot 14. \ end{align}]
Ноябрь — это 11-й месяц в году, поэтому нам нужно найти ${{a}_{11}}$:
[{{a}_{11}}=62+10cdot 14=202]
Следовательно, в ноябре будет изготовлено 202 детали.
Ответ: 202
Задача №12. Переплётная мастерская переплела в январе 216 книг, а в каждый следующий месяц она переплетала на 4 книги больше, чем в предыдущий. Сколько книг переплела мастерская в декабре?
Решение. Всё то же самое:
$begin{align} & {{a}_{1}}=216;quad d=4; \ & {{a}_{n}}=216+left( n-1 right)cdot 4. \ end{align}$
Декабрь — это последний, 12-й месяц в году, поэтому ищем ${{a}_{12}}$:
[{{a}_{12}}=216+11cdot 4=260]
Это и есть ответ — 260 книг будет переплетено в декабре.
Ответ: 260
Что ж, если вы дочитали до сюда, спешу вас поздравить: «курс молодого бойца» по арифметическим прогрессиям вы успешно прошли. Можно смело переходить к следующему уроку, где мы изучим формулу суммы прогрессии, а также важные и очень полезные следствия из неё.
Смотрите также:
- Формула n-го члена арифметической прогрессии
- Нахождение элементов арифметической прогрессии
- Тест к уроку «Сложные выражения с дробями» (легкий)
- Как считать логарифмы еще быстрее
- Задача B5: метод узлов
- Сфера, вписанная в куб
Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией
Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 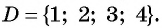
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 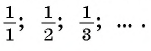
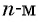
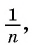
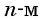
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 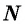
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 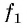
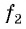
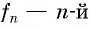
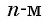
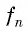
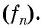
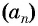
Если 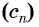
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 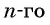
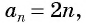
С помощью формулы 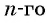
Например, пусть последовательность 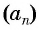
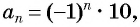
Чтобы найти некоторый член последовательности с помощью формулы 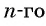
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 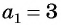
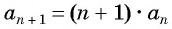
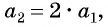
Пример №1
Найдите несколько членов последовательности 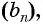
Решение:
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 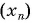
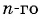
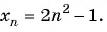
Решение:
Пример №3
Последовательность задана формулой 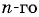
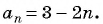
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 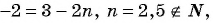
б) 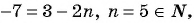
Пример №4
Для каких членов последовательности 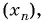
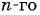
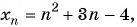
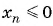
Решение:
Подставим в неравенство 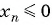
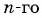
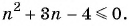
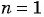
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 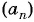
Решение:
Пример №6
Запишите несколько первых членов последовательности 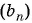
Задайте эту последовательность формулой 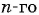
Решение:
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 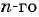
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С — 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С — 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С — 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
Число 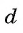
Из равенства 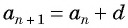
Чтобы задать арифметическую прогрессию 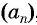
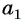
Например, если 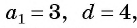
Если 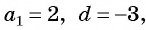
Если 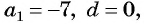
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 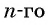
Выведем эту формулу. Если 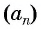
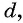
Сложим эти равенства:
После упрощения получим:
Так как число слагаемых 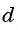
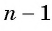
Получили формулу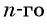
Формула 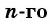
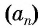
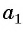
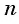
Пример №7
Последовательность 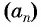
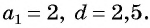
Решение:
По формуле 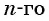
Ответ: 249,5.
Пример №8
Последовательность 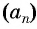
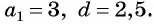
Решение:
а) По условию 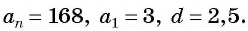
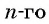
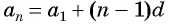
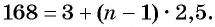
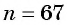
б) Подставим значения 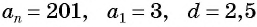
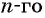
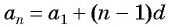
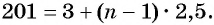
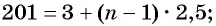
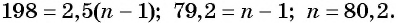
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 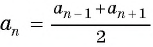
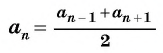
Доказательство. В арифметической прогрессии 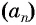
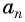
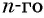
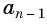
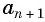
Найдем их среднее арифметическое:
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 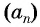
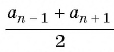
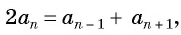
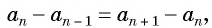
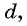
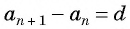
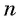
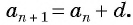
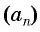
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
Решение:
Запишем для 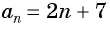
Найдем среднее арифметическое этих членов:
По характеристическому свойству арифметической прогрессии последовательность 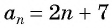
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 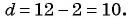
Пример №11
Известны члены арифметической прогрессии: 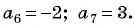
Решение:
Найдем разность арифметической прогрессии:
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 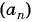
Решение:
По формуле 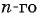
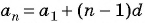
Пример №13
Запишите формулу 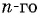
Решение:
По условию 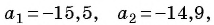
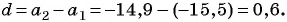
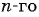
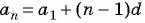
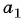
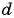
Подставим 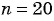
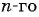
Пример №14
В арифметической прогрессии 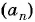
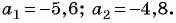
Решение:
Так как 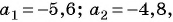
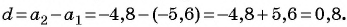
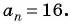
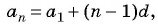
Пример №15
В арифметической прогрессии 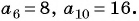
Решение:
По условию
Решим систему уравнений
Вычтем из второго уравнения первое, получим 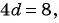
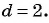
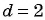
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 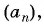
Решение:
По характеристическому свойству арифметической прогрессии 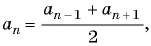
Пример №17
При каком значении 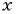
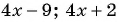
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии 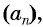
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 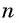
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е.
В общем виде:
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 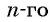
Тогда получим:
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 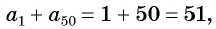
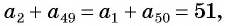
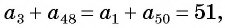
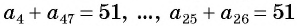
Выведем формулу суммы 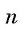
Обозначим 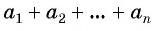
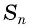
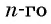
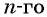
Сложим эти два равенства и получим:
По свойству 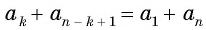
Число всех таких пар сумм равно 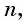
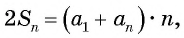
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 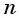
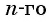
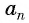
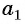
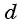
Если известен первый член прогрессии и разность, то удобно использовать формулу
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 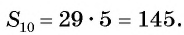
Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 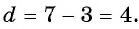
для и получим:
Ответ: 5050.
Пример №19
В арифметической прогрессии 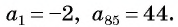
Решение:
Применим формулу суммы 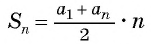
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
так как 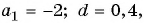
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 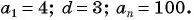
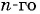
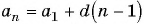
Воспользуемся формулой суммы 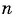
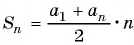
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 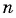
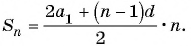
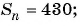
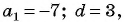
Так как 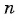
Пример №23
В арифметической прогрессии 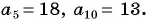
Решение:
Найдем 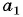
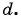
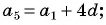
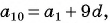
Решим полученную систему способом сложения:
Тогда
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 — 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна:
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 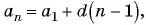
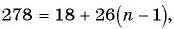
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 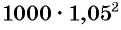
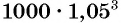
Через шесть лет сумма будет равна
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
Число 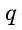
Из равенства 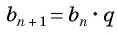
Чтобы задать геометрическую прогрессию 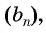
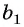
Например, если 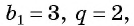
Если 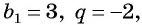
Если 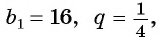
вид
Если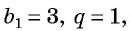
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 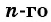
Выведем эту формулу. Если 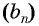
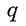
Перемножим эти равенства между собой:
Разделим обе части равенства на произведение 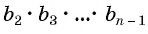
Так как число множителей 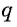
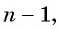
Получили формулу 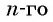
Формула 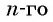
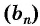
Пример №25
Последовательность 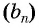
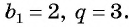
Решение:
По формуле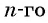
Ответ: 4374.
Пример №26
Последовательность 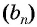
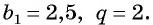
Решение:
По условию 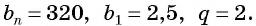
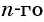
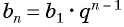
Решим это уравнение:
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 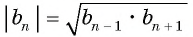
или 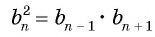
Доказательство:
В геометрической прогрессии 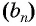
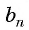
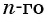
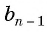
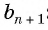
Найдем среднее пропорциональное (среднее геометрическое) соседних с 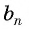
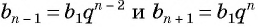
Выполним преобразования в правой части равенства:
откуда получим, что
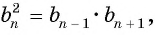
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 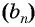
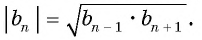
Тогда 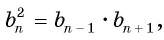
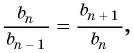
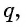
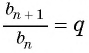
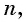
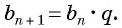
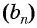
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой
Решение:
Запишем для 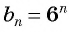
Найдем среднее пропорциональное этих членов:
По характеристическому свойству геометрической прогрессии последовательность 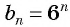
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 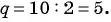
Пример №29
Известны члены геометрической прогрессии:
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 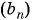
Решение:
По формуле 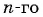
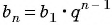
Пример №31
Запишите формулу 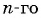
Решение:
По условию 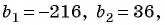
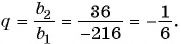
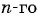
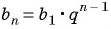
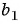
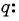
Подставим 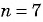
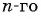
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
Известно, что 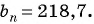
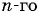
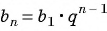
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 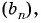
Решение:
По условию
Составим систему уравнений
Разделим второе уравнение на первое и получим:
Подставим это значение 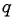
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 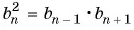
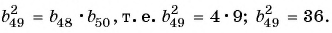
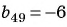
Пример №35
При каком значении 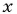
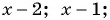
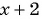
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).
Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 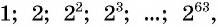
Выведем формулу, по которой можно находить сумму 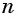
Обозначим сумму 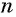
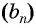
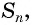
Умножим обе части этого равенства на знаменатель прогрессии 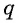
Вычтем из второго равенства первое и получим:
т. e. 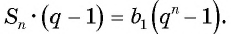
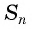
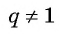
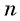
Если 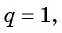
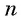
Формула суммы n первых членов геометрической прогрессии:
Вычислим по формуле суммы 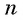
Первый член геометрической прогрессии 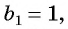
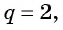
Тогда
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 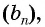
Решение:
Применим формулу суммы 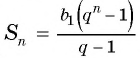
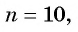
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 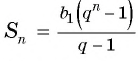
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 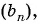
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
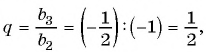
По формуле 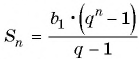
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если
Решение:
Подставим в формулу 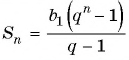
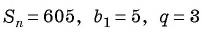
Пример №40
В геометрической прогрессии 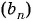

Решение:
Найдем знаменатель прогрессии:
Подставим в формулу 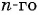
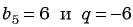
По формуле 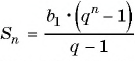
Пример №41
В геометрической прогрессии 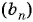
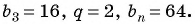
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 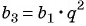
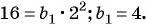
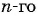
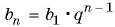
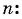
По формуле суммы 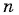
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 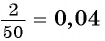
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 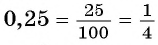
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 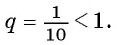
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель
Например, геометрическая прогрессия 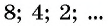
Геометрическая прогрессия 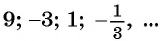
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 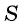
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 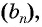
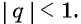
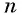
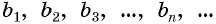
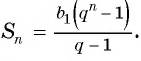
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 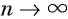
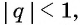
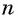
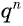
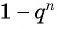
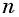
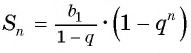
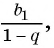
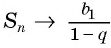
Число 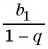
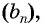
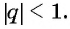
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 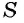
Вычислим по этой формуле сумму разрядных слагаемых:
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 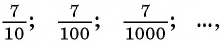
а знаменатель равен
Сумма бесконечно убывающей геометрической прогрессии:
Так как 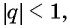
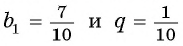
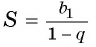
Значит,
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 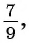
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
, и найти знаменатель этой прогрессии
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число
(1)
(2)
(3)
(4)
(5)
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 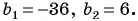
Решение:
Найдем знаменатель прогрессии: 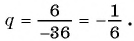
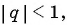
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а)
б)
в)
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 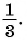
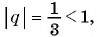
б) Поскольку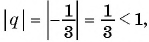
в) Знаменатель прогрессии 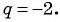
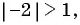
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 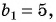
Решение:
По формуле 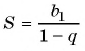
Пример №45
В бесконечно убывающей геометрической прогрессии 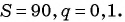
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 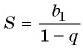
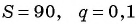
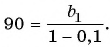
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1)
(2)
(3)
(4)
(5)
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства

















































![{displaystyle a_{n}+a_{m}=2a_{1}+(n+m-2)d=2a_{1}+(k+l-2)d=[a_{1}+(k-1)d]+[a_{1}+(l-1)d]=a_{k}+a_{l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/986721b4a1b32b83fa421239db5e94bd1590877d)





























































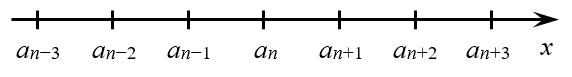

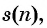

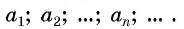
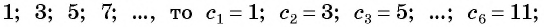
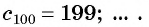
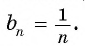
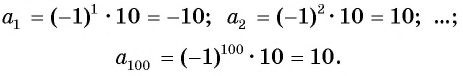
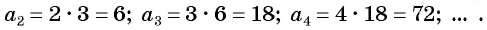
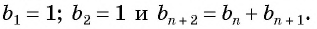
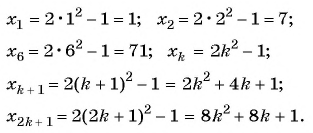
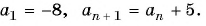
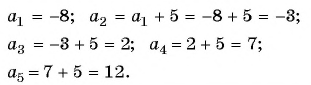
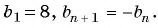
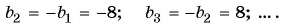
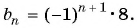
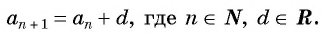
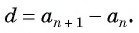
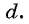
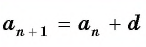
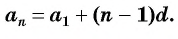
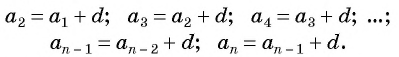
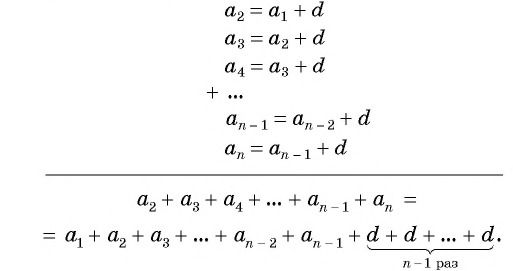
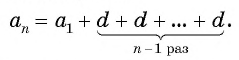
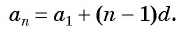

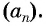
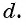
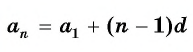
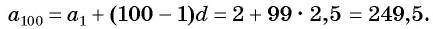
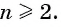
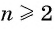
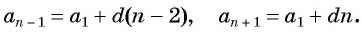
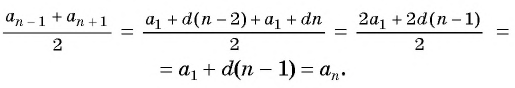
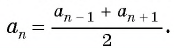
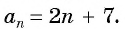
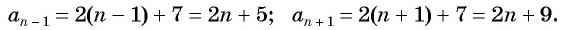
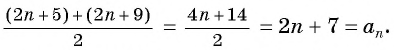
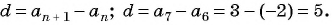
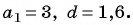
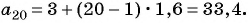
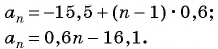
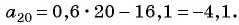
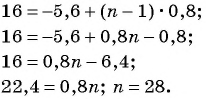
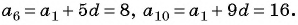
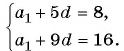
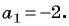
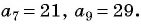
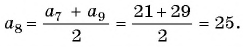
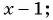
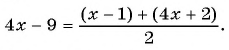
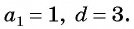
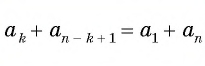
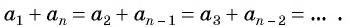
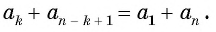
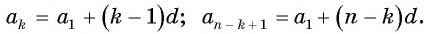
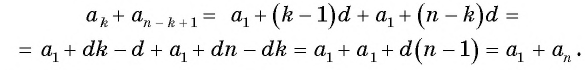
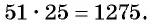
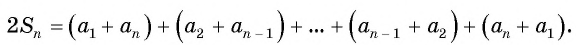
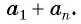
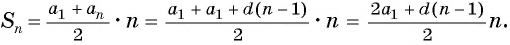
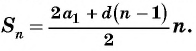
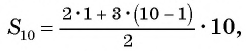

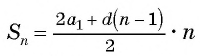
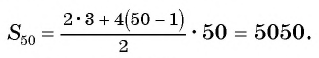
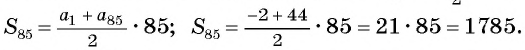
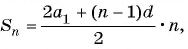
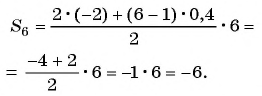
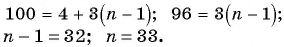
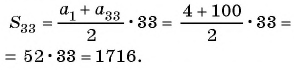
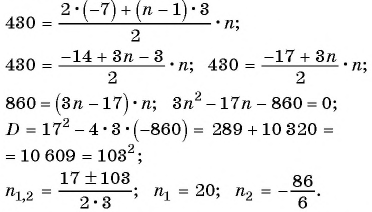
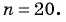
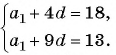
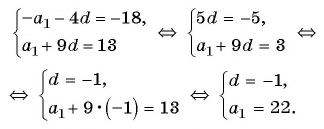
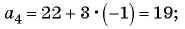
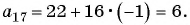
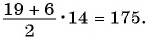
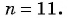
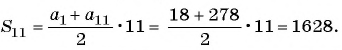
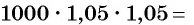
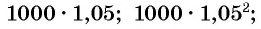
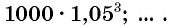
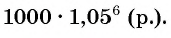
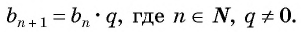
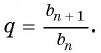
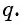
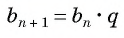
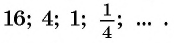
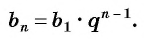
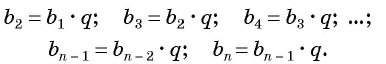
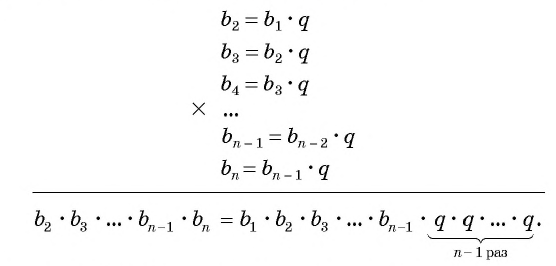
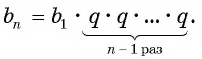
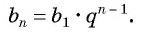
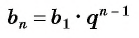
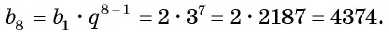
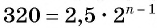
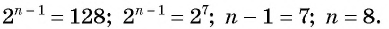
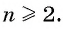
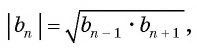
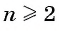
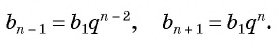
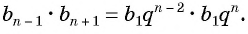
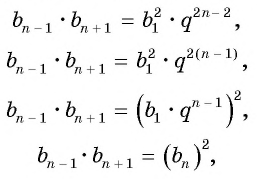
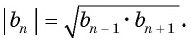
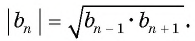
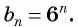
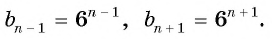
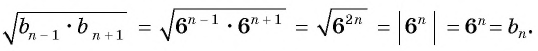
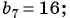
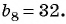
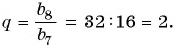
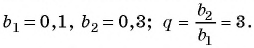
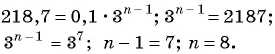
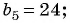
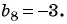
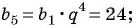
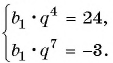
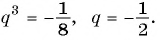
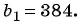
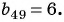
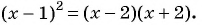
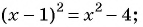
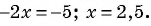

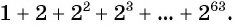
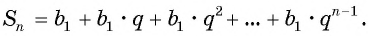
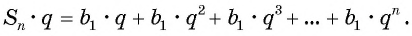
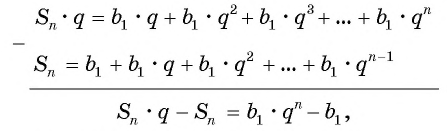
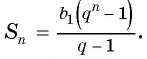
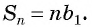
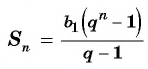
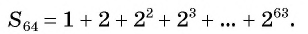
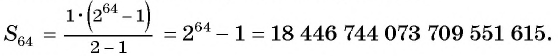
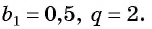
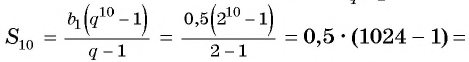
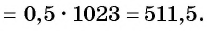
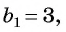
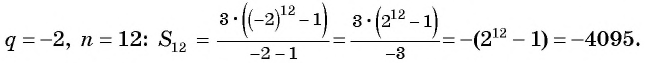
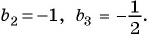
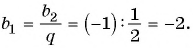
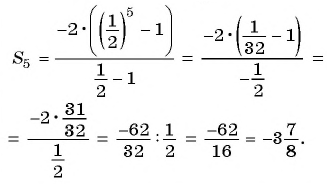
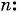
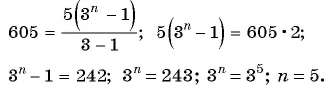
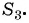
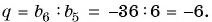
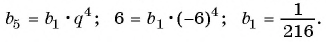
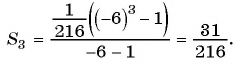
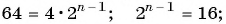
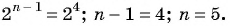
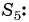
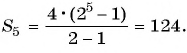
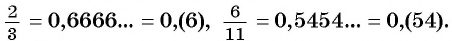
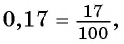
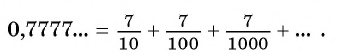
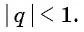
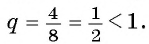
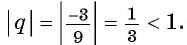
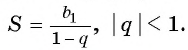
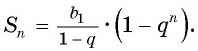
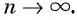
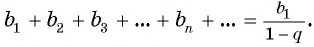
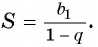
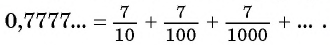
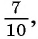
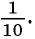
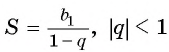
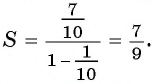
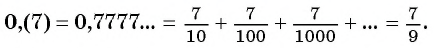
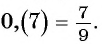
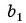 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии