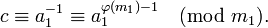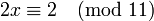Z /nZ
Z /nZ
факторизации базируются многие современные криптографические системы. Более подробно об этом мы будем вести речь в третьей главе первой части данного пособия.
|
Пусть |
n 1 фиксированное |
натуральное |
число. |
Множество |
Z/nZ 0,1,…,n 1 всевозможных остатков от деления целых чисел на n называется кольцом классов вычетов по модулю n. На множестве опреде-
|
лены операции сложения и умножения |
по правилам: суммой (произведе- |
|
|
нием) |
классов a, b Z /nZ называется |
класс, равный остатку от деления |
|
a b |
(a b) на n. Ввиду такой специфики операций элементы Z /nZ будем |
обозначать символами a вместо a. Оказывается, операции такого остаточного сложения и умножения наследуют основные свойства сложения и умножения целых чисел. Ввиду конечности количества элементов остаточное сложение и умножение можно задавать в виде таблиц.
Пример 1.2.1. Запишем таблицы сложения и умножения элементов в кольце классов вычетов Z /3Z :
|
0 |
1 |
2 |
|||||||||||||
|
0 |
0 |
||||||||||||||
|
1 |
2 |
||||||||||||||
|
1 |
1 |
2 |
0 |
||||||||||||
|
0 |
|||||||||||||||
|
2 |
2 |
1 |
0 1 2
0 0 0 0
1 0 1 2
2 0 2 1
Таблицы ярко демонстрируют экзотичность операций в кольце классов вычетов. Здесь, как видим, сумма ненулевых классов может равняться нулю, а «дважды два» далеко не четыре, а 1. Это означает, что класс 2 является обрат-
|
ным самому себе. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Определение 1.2.1. Элемент |
Z / mZ |
называется обратимым, |
если най- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
k |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дется такой класс |
Z / mZ, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
что k |
l |
l k |
1 |
. Тогда класс вычетов |
на- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
l |
l |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
зывают обратным к классу вычетов |
и его обозначают символом |
1. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
k |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 1.2.2. Приведем таблицу умножения в кольце Z /8Z |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||||||||||||||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||||||||||||||||||||||||||||||||||||||||||
|
0 |
6 |
0 |
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
4 |
2 |
4 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
0 |
3 |
6 |
7 |
5 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
4 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
0 |
4 |
0 |
4 |
0 |
4 |
0 |
4 |
||||||||||||||||||||||||||||||||||||||||||||
|
5 |
0 |
5 |
7 |
6 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
4 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
0 |
6 |
0 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
4 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
7 |
0 |
7 |
6 |
5 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
1 |
7

В данном примере, как видим из таблицы умножения, обратимыми явля-
ются 4 класса вычетов (половина элементов кольца): 1, 3, 5, 7. Классы
0, 2, 4, 6 не являются обратимыми. В кольце Z мы наблюдали однозначность разложения на множители и существование простых чисел. Здесь эти свойства теряются: 2 3 6 2 5 6 7; 4 2 2 2 6 4 7 4 3; 6 2 3 2 7 5 6.
Неоднозначность разложения на множители налицо, при этом ни один из необ-
ратимых классов нельзя отнести к разряду простых: 2 делится и на себя и на
6, 4 делится и на 2 и на 6, 6 делится и на себя и на 2.
Эмпирически определить наличие обратных элементов у данного класса k можно по таблице умножения: если в k -й строке этой таблицы найдется элемент 1, то первый элемент столбца, в котором находится найденный класс 1, и
есть обратный к классу k.
Разумеется, реально построить таблицу умножения можно лишь для небольших значений m. Отметим свойства строк таблиц умножения в общем случае.
Лемма 1.2.1. Пусть k такой класс кольца Z / mZ, что НОД (k, m) 1. То-
гда: 1) для каждого l 0 произведение k l 0, 2) k l k s , если l s; 3) отображение k :Z /mZ Z /mZ, действующее по правилу k (x) k x,
является взаимно однозначным; 4) k – обратимый класс в кольце Z / mZ. Лемма 1.2.2. Пусть k Z / mZ, такой, что НОД(k,m) d 1. Тогда:
1) существует такой ненулевой класс l Z / mZ, что k l 0;
2) найдутся ненулевые классы l1, l2 Z / mZ, такие, что k l1 k l2;
3) k l 1 для всех классов l Z / mZ, следовательно, класс k необратим в кольце Z / mZ.
Из лемм 1.2.1 и 1.2.2 вытекает
Критерий обратимости классов вычетов. Класс k Z / mZ обратим в этом кольце тогда и только тогда, когда НОД(k,m) 1. Если обратный к дан-
ному классу k Z / mZ существует, то он также обратим. Произведение обратимых классов кольца Z / mZ есть также обратимый класс. В частности, если m p простое число, то в кольце Z / mZ каждый ненулевой класс обратим.
Определение 1.2.2. Множество Z /mZ всех обратимых элементов кольца Z /mZ называется мультипликативной группой этого кольца.
Из критерия вытекает следующий алгоритм нахождения обратного класса к данному классу k Z / mZ. Вычисляем по алгоритму Евклида НОД(k,m).
Если НОД(k,m) d 1, то класс k необратим. Пусть НОД(k,m) 1. Для чисел k и m с помощью расширенного алгоритма Евклида строим соотношение Безу ku mv 1. Это равенство влечет соответствующее равенство классов
8

вычетов: k u m v 1 . Мы знаем, что m 0. Следовательно, имеем ра-
венство k u 1, которое и означает, что k 1 u. При этом часто оказывает-
|
ся, что u 0,1,…, m 1 . Поэтому формальная запись |
k |
1 |
u |
требует дора- |
|||||||||||||||
|
ботки. Если |
u m, то |
следует подобрать |
такое |
целое t 1, что |
|||||||||||||||
|
u tm 0,1,…,m 1 . Тогда |
1 |
. |
Если же u 0, |
то следует подобрать |
|||||||||||||||
|
k |
u tm |
||||||||||||||||||
|
такое целое t 1, что u tm 0,1,…, m 1 . Тогда |
1 |
. |
|||||||||||||||||
|
k |
u tm |
||||||||||||||||||
|
Пример 1.2.3. В кольце Z / 201Z найдем |
1. |
||||||||||||||||||
|
37 |
НОД(37, 201). |
||||||||||||||||||
|
Решение. |
С помощью |
алгоритма |
Евклида |
найдем |
|||||||||||||||
|
201 37 5 16; |
37 16 2 5; |
16 5 3 1. |
Таким образом, НОД(37, 201) 1 и |
37 1 существует. Из полученных равенств алгоритма Евклида построим соот-
|
ношение Безу для чисел |
201 и 37: |
1 201 7 37 ( 38). Следовательно, |
||||||||
|
1 |
Проверка: |
163 37 6031 201 30 1 1(mod201). |
||||||||
|
37 |
38 |
201 38 |
163. |
Значит, действительно 37 163 1.
Малая теорема Ферма. Пусть p простое число и целое число a не де-
лится на p. Тогда ap 1 1 в кольце Z / pZ.
Определение 1.2.3. Функция Эйлера – функция (m) натурального аргумента m, которая каждому натуральному числу m 1 ставит в соответствие количество натуральных чисел, меньших m и взаимно простых c m.
Функция Эйлера определяет количество обратимых элементов в кольце
Z /mZ, т. е. порядок группы Z /mZ . Эта функция обладает рядом мультипликативных свойств, облегчающих вычисление ее значений.
Свойство 1. (p) p 1 для каждого простого числа p. Для каждого составного n значение (n) n 1.
Свойство 2. (pn) pn pn 1 для каждого простого числа p и произ-
вольного натурального n 1.
Свойство 3. Если НОД(n,m) 1, то (n m) (n) (m).
|
Свойство 4. Если n ps1 |
ps2 |
…pst |
– каноническое разложение числа n, то |
||||||
|
1 |
2 |
t |
|||||||
|
1 |
1 |
1 |
|||||||
|
(n) 1 |
1 |
… 1 |
. |
||||||
|
pt |
|||||||||
|
p1 |
p2 |
||||||||
|
Пример 1.2.4. Вычислим (48). |
Поскольку 48 3 24, то согласно свой- |
ству 4 (48) 48 (1 1/3) (1 1/ 2) 16.
Пример 1.2.5. Из критерия обратимости классов вычетов следует, что в кольце Z / mZ имеется в точности (m) обратимых классов. Например, (12) 4. Значит, в кольце Z /12Z имеется именно 4 обратимых элемента. Непосредствен-
ная проверка показывает, что этими классами являются 1, 5, 7,11.
9
Все вычеты из (4) и только они
удовлетворяют сравнению (3) и равносильному ему сравнению . По модулю
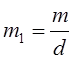
числа из (4) принадлежат одному классу. По модулю они
принадлежат различным классам:
Следовательно, сравнение имеет
решений:
,
,…,
.
Пример. . Так как
,
, то сравнение имеет 3 решения. Делим обе
части и модуль на 3, получаем: . Решениями сравнения
будут:
,
,
.
Пример. . Т.к.
,
, то сравнение имеет 3 решения. После
деления обеих частей и модуля на 3 получим сравнение:
.
Решение этого сравнения: .
Решения заданного сравнения: ,
,
.
Порядок класса вычетов. Первообразные корни. Индексы.
1. Порядок класса вычетов.
Изучим подробнее строение группы
, состоящей из обратимых элементов в кольце
вычетов . Эта группа состоит из классов вычетов
взаимно простых с модулем и содержит
классов вычетов.
Так как умножение в кольце коммутативно, то
—
коммутативная группа, состоящая из элементов. Поэтому все
элементы группы
(т.е.
все классы вычетов по модулю , взаимно простые с
) имеют конечный порядок и этот порядок –
делитель (это следует из теоремы Лагранжа). Учитывая
определение порядка элемента в группе, получаем следующее определение
порядка класса вычетов:
Определение 1. Порядком
класса вычетов , взаимно простого с модулем
, называется наименьшее натуральное число
, такое, что
.
Число называют
также порядком всех чисел , входящих в класс
вычетов . Если
, то из
равенства следует, что
. Итак,
получаем следующее:
Определение 2.
Пусть число взаимно просто с
,
.
Порядком числа по модулю
называется
наименьшее натуральное число , такое, что
.
Если порядок класса вычетов (соответственно числа
) по модулю
равен
, то
называется
показателем (числа
)
по модулю , или что
(
) принадлежит показателю
по модулю
.
Если порядок класса вычетов по модулю
равен
, то циклическая подгруппа, порождённая
классом вычетов в группе
,
состоит из элементов. И можно применить к этой
подгруппе все результаты о циклических подгруппах (см…..).
В частности, имеет место:
Теорема 1. Если и порядок
по
модулю равен
, то
тогда и только тогда, когда
делится на
.
Следствие 1. Если
порядок класса вычетов по модулю
равен
, то
тогда и только тогда, когда
, т.е
делится
на .
Следствие 2. Если
порядок класса вычетов по модулю
равен
, то все
классы вычетов различны.
Теорема 2. Если
порядок класса вычетов по модулю
равен
, то
порядок класса вычетов равен
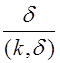
Следствие. Если
порядок класса вычетов по модулю
равен
, то
среди классов вычетов порядок
имеют
классов.
Доказательство. По
следствию 2 из теоремы 1 все классы вычетов различны.
Порядок имеют те из этих классов, для которых
. Число таких классов равно
.
Пример. Найдём
порядок класса вычетов по модулю
, а также все классы вычетов по этому
модулю, порядок которых равен порядку класса вычетов
Порядок любого класса вычетов
является делителем числа , следовательно порядок
класса вычетов по модулю
— это делитель числа
. Натуральные делители числа
— числа
. Будем
возводить число в степени с показателями
до тех пор, пока не получим число,
сравнимое с по модулю
. Имеем:
,
,
,
. Итак,
порядок числа 7 по модулю 43 равен 6
Чтобы найти остальные классы
вычетов по модулю 43, имеющие порядок 6, рассмотрим числа 0,1,2,3,4,5. Выбираем
из них взаимно простые с , т.е 1 и 5. Значит,
искомые классы вычетов: и
. Но
.
Получили: искомые классы вычетов и
.
2. Первообразные корни по простому модулю.
Пусть — простое число. Группа
обратимых элементов кольца
состоит из классов вычетов
. По теореме 1 порядок каждого из этих
классов вычетов является делителем числа .
Определение 3. Первообразным корнем по
простому модулю называется класс вычетов
по этому модулю, порядок которого равен
.
По следствию 2 из теоремы 1 получаем: если — первообразный корень по простому модулю
, то все степени
различны
(в этом случае ).
[1]
Интересные (и важные для приложений) примеры задания на одном множестве
одновременно нескольких операций доставляет криптография.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Вычеты и их применение
Определение вычета
Пусть — изолированная особая точка функции
. По определению изолированной особой точки существует некоторая окрестность этой точки, в которой
— аналитическая. Напомним, что для
эта окрестность имеет вид
, а для
—
.
Рассмотрим произвольный контур , принадлежащий такой окрестности и являющийся границей некоторой области, содержащей
(рис 4.2,а).
По следствию из основной теоремы Коши интеграл имеет одно и то же значение, независимо от вида кривой
, т.е. интеграл характеризует поведение функции
в особой точке
и, следовательно, может быть использован для исследования функции как некоторая числовая характеристика.
Вычетом функции в изолированной особой точке
называется интеграл
, где
— контур, принадлежащий окрестности точки
и охватывающий ее. Обход контура — положительный, т.е. область им ограниченная и принадлежащая окрестности
при обходе расположена слева: для
— обход против часовой стрелки (рис. 4.2,а), для
— по часовой стрелке (рис. 4.2,б). Обозначается вычет
(res — residu (фр.) — вычитать):
(4.16)
Так как в окрестности изолированной особой точки функция разлагается в ряд Лорана, то, используя формулы для коэффициентов ряда Лорана и сравнивая их с (4.16), замечаем, что можно сделать следующее заключение.
Утверждение 4.5. Вычет функции в изолированной особой точке равен коэффициенту при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при
для
, и этому коэффициенту, взятому с противоположным знаком, для
(4.17)
(4.18)
С помощью вычетов можно записать в другой форме основную теорему Коши для сложного контура.
Действительно, пусть функция в области имеет
особых точек
. Можно рассмотреть контуры
, которые являются границами непересекающихся областей
, таких, что каждая из особых точек
(изолированных особых точек) принадлежит одной из
(рис. 4.3,а), а интеграл по
согласно определению (см. формулу (4.16)) есть
.
Кроме того, для любого контура , ограничивающего область
, которой принадлежат все особые точки функции
, и контура
— границы окрестности бесконечно удаленной точки справедливо равенство
(обход на
по часовой стрелке (рис. 4.3,б)). Из этих рассуждений и формулы (4.16) получаем следующие утверждения.
Основная теорема о вычетах
Утверждение 4.6 (основная теорема о вычетах). Если функция -аналитическая в
за исключением конечного числа особых точек
, то справедливо равенство (где
— граница области
):
(4.19)
Обобщенная теорема о вычетах
Утверждение 4.7 (обобщенная теорема о вычетах). Сумма вычетов функции во всех ее особых точках, включая бесконечно удаленную точку, равна нулю:
(4.20)
Пример 4.22. Найти вычеты следующих функций в их особых точках: а) ; б)
.
Решение
Особыми точками функций являются точки . Записываем разложения функций в ряд Лорана в окрестности этих точек (см. примеры 3.31, 3.33 и 3.34):
а)
Из этих разложений находим:
Полученный результат иллюстрирует обобщенную теорему о вычетах:
Заметим также, что здесь точки и
— простые полюсы, а
— устранимая особая точка.
б)
Из этих разложений имеем:
Вычет в бесконечно удаленной точке можно найти, используя обобщенную теорию о вычетах:
. Этот же результат получим, если запишем разложение функции в области
-окрестности
Заметим, что для этой функции —
,
—
, а
— устранимая особая точка.
Пример 4.23. Найти вычеты следующих функций в особых точках: а) ; б)
.
Решение
Пример 4.24. Найти вычеты следующих функций в их особых точках: a) ; б)
.
Решение
Конечные особые точки функций являются существенно особыми точками. Это для первой функции и
для второй. Разложим функции в ряды в окрестностях этих точек и найдем вычеты по формуле (4.17):
а)
Следовательно, .
Так как у рассматриваемой функции другах конечных особых точек нет, то по формуле (4.20) . Заметим, что
— устранимая особая точка для данной функции
;
б)
поэтому . Поскольку нет другах конечных особых точек, то по формуле (4.20)
. Точка
является полюсом первого порядка данной
.
Вычисление вычетов в полюсе и устранимой особой точке
В рассмотренных выше примерах при нахождении вычетов использовались формулы (4.17),(4.18) , т.е. функции раскладывались в ряды Лорана. При этом знание типа особой точки, в которой вычисляется вычет функции, не является обязательным. Таким методом всегда определяется вычет в тех случаях, когда заранее предполагается, что особая точка — существенно особая точка для функции. В случае устранимой особой точки и полюсов задачу вычисления вычета по формуле (4.17) можно заменить некоторыми практически более удобными формулами и правилами. Вывод этих формул и правил в общем виде, очевидно, связан с исследованием разложения функции в ряд в окрестности особой точки, а тип особой точки определяется по поведению функции, т.е. вычислением предела.
Так, если и
— конечная особая точка, то в разложении функции в ряд Лорана в окрестности
, согласно утверждению 4.1, отсутствует главная часть. Следовательно,
и
.
Если и
— полюс функции
, то можно определить порядок полюса, также не прибегая к разложению функции в ряд, используя утверждение 4.3. Пусть
—
функции
, тогда разложение функции в ряд в окрестности
имеет вид (4.6). Умножив обе части равенства на
и продифференцировав результат
раз, получим выражение
из которого определяем .
В частности, при имеем
. Последнее равенство принимает наиболее удобную форму для функции вида
, где
— аналитические вточке
функции и
. А именно:
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 4.8
1. Если конечная особая точка является устранимой особой точкой функции
, то (где
— устранимая особая точка)
(4.21)
2. Если полюс порядка п функции
, то
(4.22)
(4.23)
3. Если —
функции
, где
— аналитические в точке
функции и
, то
(4.24)
Алгоритм вычисления вычета функции
Замечание 4.6. Формула (4.22) дает следующий алгоритм вычисления вычета функции в полюсе порядка .
1. Умножить на
, где
— порядок полюса
, и получить функцию
.
2. Найти производную функции порядка
.
3. В соответствии с (4.22) найти .
Пример 4.25. Найти вычеты в конечных особых точках функций:
Решение
Конечными особыми точками являются
и
— полюсы первого порядка, причем в каждом случае функцию можно представить в виде, допускающем применение формулы (4.24). Используя эту формулу, находим
Для функции точка
также является
и выполняются условия применимости формулы (4.24) . При этом функцию удобно представить в виде
. Применяя формулу (4.24), находим
Точка для
— полюс второго порядка. Применяем формулу (4.22) при
. Запишем решение согласно алгоритму.
1. Умножаем на
и записываем функцию
.
2. Находим производную функции
3. Используя (4.22), получаем .
Для функции единственная конечная особая точка
является устранимой особой точкой, поэтому
(согласно (4.21)).
Все полученные результаты соответствуют результатам примеров 4.22 и 4.23.
Пример 4.26. Найти вычеты следующих функций в особых точках: а) ; б)
;
Решение
В заключение раздела рассмотрим бесконечно удаленную точку в случае, когда она является устранимой особой точкой для . Разложение функции в ряд Лорана имеет вид (4.5). Коэффициент
можно определить из этого равенства следующим образом:
. Так как, очевидно,
, то, доопределяя функцию, положим
. Получаем формулу для вычисления вычета в
— устранимой особой точке функции
(4.25)
В частности, если является нулем функции
, то есть
, то формула принимает вид
(4.26)
Пример 4.27. Найти вычеты в бесконечно удаленной точке функций:
а) ; б)
.
Решение
а) Точка — устранимая особая точка для этих функций и
. Поэтому вычеты этих функций находим по формуле (4.26):
Результат совпадает с полученным в примере 4.22.
б) Точка — устранимая особая точка для
, так как
. Вычет находим по формуле (4.25):
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.
В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.
Содержание
- 1 Определения
- 2 Свойства
- 3 Классы вычетов
- 4 Решение сравнений
- 4.1 Сравнения первой степени
- 4.2 Сравнения второй степени
- 5 История
- 6 Ссылки
Определения
Говорят, что два целых числа a и b сравнимы по модулю натурального числа n, если при делении на n они дают одинаковые остатки.
Эквивалентные формулировки: a и b сравнимы по модулю n, если их разность a — b делится на n, или если a может быть представлено в виде a = b + kn, где k — некоторое целое число.
- Пример: 32 и −10 сравнимы по модулю 7, так как 32 = 7∙4 + 4, −10 = 7∙(-2) + 4.
Утверждение «a и b сравнимы по модулю n» записывается в виде:
Свойства
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
то
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 
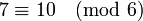
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
Другие свойства:
Классы вычетов
Множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n, и обычно обозначается [a]n или 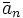
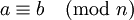
Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел 

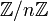
Операции сложения и умножения на 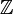

- [a]n + [b]n = [a + b]n
Относительно этих операций множество 
Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
- Если b не кратно d, то у сравнения нет решений.
- Если b кратно d, то у сравнения существует единственное решение по модулю m / d, или, что то же самое, d решений по модулю m. В этом случае в результате сокращения исходного сравнения на d получается сравнение:
где a1 = a / d, b1 = b / d и m1 = m / d являются целыми числами, причем a1 и m1 взаимно просты. Поэтому число a1 можно обратить по модулю m1, то есть найти такое число c, что 

Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Пример: решим уравнение 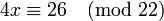
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: 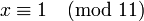
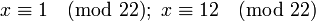
Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Ссылки
- Вейль А., Основы теории чисел, М.:Мир, 1972.
- Виленкин Н. Я., Сравнения и классы вычетов, Квант, № 10, 1978.
- Виноградов И. М., Основы теории чисел, М.: ГИТТЛ, 1952.
Wikimedia Foundation.
2010.

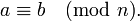

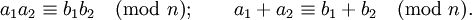
![[a]_ncdot [b]_n=[acdot b]_n](https://dic.academic.ru/pictures/wiki/files/99/cb8dd8e51b2583aa2bcaa03446e485c3.png)