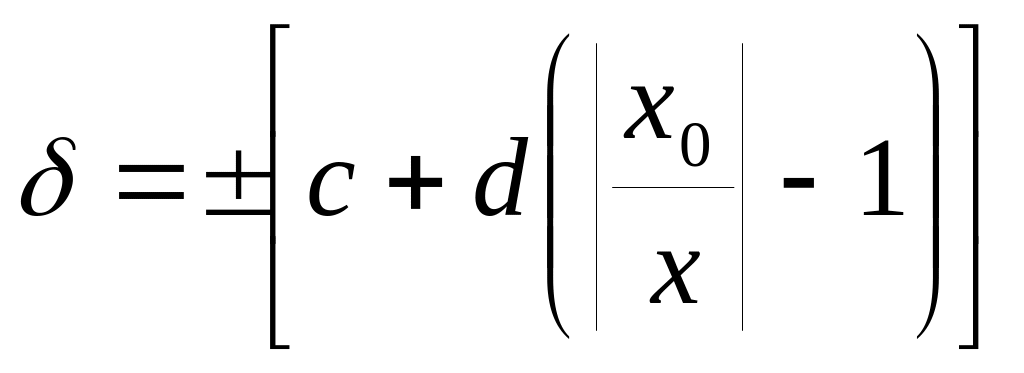Как найти класс точности по приведенной погрешности

Приведенная в
предыдущем параграфе номенклатура МХ
в известном смысле предполагает строгое
нормирование МХ СИ, используемых при
высокоточных лабораторных измерениях
и мет­рологической аттестации, других
СИ.

При технических
измерениях, когда не предусмотрено
выде­ление случайных и систематических
составляющих, когда не су­щественна
динамическая погрешность СИ, когда не
учитываются влияющие (дестабилизирующие)
факторы и т.д., можно пользо­ваться
более грубым нормированием — присвоением
СИ опреде­ленного класса точности по
ГОСТ 8.401—80.

Класс
точности —
это обобщенная МХ, определяющая раз­личные
свойства СИ. Например, у показывающих
электроизме­рительных приборов класс
точности помимо основной погреш­ности
включает также вариацию показаний, а у
мер электричес­ких величин — величину
нестабильности (процентное изменение
значения меры в течение года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
явля­ется непосредственной
характеристикой точности измерений,
вы­полняемых с помощью этих СИ,
поскольку точность измерения зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.

В частности, чтобы
измерить величину с точностью до 1%,
недостаточно выбрать СИ с погрешностью
1%. Выбранное СИ дол­жно обладать
гораздо меньшей погрешностью, так как
нужно учесть как минимум еще погрешность
метода.

Правда,
в некоторых случаях возможна и
противоположная ситуация, когда
погрешность измерения меньше погрешности
прибора (нулевые методы измерения).
Например, схема измере­ния построена
так, что стрелка нуль-индикатора при
разности измеряемых величин, равной
1%,
отклоняется
полностью на100
делений. Пусть погрешность нуль-индикатора
равна одному де­лению.
В этом случае возможен остаточный
разбаланс также на одно деление, равный
1% однопроцентной разности измеряемых
величин. Тогда относительная погрешность
измерения не превы­сит
0,01%, т. е. составит одну сотую относительной
погрешности нуль-индикатора.
Однако рассмотренный случай можно
отнести к исключениям
из общего правила.

В
связи с большим разнообразием как самих
СИ, так и их МХ,
ГОСТ 8.401—80 устанавливает несколько
способов назначе­ния
классов точности. При этом в основу
заложены следующие поло­жения:

• в
  качестве норм служат пределы допускаемых
  погрешнос­тей,
  включающие систематические и случайные
  составляющие;

• основная
  δ_осн
  и все виды дополнительных погрешностей
  δ_осн
  нормируются
  порознь (см. п. 3.2).

Первое
положение свидетельствует о необходимости
разраба­тывать
СИ с учетом однократного отсчета
показаний по величине общей
погрешности.

Второе
положение направлено на обеспечение
максимальной однородности однотипных
СИ.

Например,
можно обеспечить

,
за счет любого δ_i
Од­нако
замена одного СИ другим не всегда будет
эквивалентной, поскольку
одно СИ будет иметь большую температурную
погреш­ность,
другое — частотную, что при конкретном
измерении не­известно.

Определяя
класс точности, нормируют прежде всего
пределы допускаемой
основной погрешности δ_осн.
Пределы допускаемой до­полнительной
погрешности устанавливают в виде
дольного (крат­ного)
значения [δ_осн].

Классы
точности присваивают СИ при их разработке
по резуль­татам
государственных приемочных испытаний.
Если СИ предназна­чены
для измерения одной и той же физической
величины, но в разных
диапазонах, или — для измерения разных
физических вели­чин,
то этим СИ могут присваиваться разные
классы точности как по
диапазонам, так и по измеряемым физическим
величинам.

В
эксплуатации СИ должны соответствовать
этим классам точ­ности.
Однако при наличии соответствующих
эксплуатационных требований класс
точности,
присвоенный
на производстве, в экс­плуатации
может понижаться.

Пределы
допускаемых основной и относительной
погрешнос­тей выражают в форме
абсолютной, относительной или приве­денной
погрешностей. Способ выражения
погрешностей зависит от
характера изменения погрешности по
диапазону измерения, назначения
и условий применения СИ.

Если
погрешность результатов измерений в
данной области измерений
принято выражать в единицах измерений
величины или делениях
шкалы, то принимается форма абсолютных
погрешнос­тей
(меры, магазины номинальных физических
величин). Если границы
абсолютных погрешностей в пределах
диапазона измерений
практически постоянны, то принимается
форма приведен­ной
погрешности, а если эти границы нельзя
считать постоянны­ми,
то форма относительной погрешности.

Поэтому
ГОСТ 8.401—80 в качестве основных
устанавливает три
вида классов точности СИ:

• для
  пределов допускаемой абсолютной
  погрешности в еди­ницах
  измеряемой величины или делениях шкалы;

• для
  пределов допускаемой относительной
  погрешности в виде ряда
  чисел

, (3.4)

где
А=1;
1,5;
(1,6); 2; 2,5; (3); 4; 5 и 6; значения 1,6 и 3 —
допус­каемые,
но не рекомендуемые; п
= 1;
0; -1; -2; …;

• для
пределов допускаемой приведенной
погрешности с тем

же
рядом (3.4): γ = ± А10ⁿ.

Абсолютная
погрешность может выражаться одним
числом Δ
= ±а
при
неизменных границах, двучленом Δ = ±
(а + bх)
—
при линейном
изменении границ абсолютной погрешности,
т.е. при совместном
проявлении аддитивной и мультипликативной
состав­ляющих
(см. рис. 3.4), или в виде таблицы, графика
функции при нелинейном
изменении границ (например, табл. 3.1).

Классы
точности СИ, выраженные через абсолютные
погреш­ности, обозначают прописными
буквами латинского алфавита или римскими
цифрами. При этом, чем дальше буква от
начала алфа­вита, тем больше значения
допускаемой абсолютной погрешнос­ти.
Например, СИ класса С более точен, чем
СИ класса М, т. е. это число — условное
обозначение и не определяет значение
погреш­ности.

Класс
точности через относительную погрешность
СИ назна­чается
двумя способами.

• Если
погрешность СИ имеет в основном
мультипликатив­ную
составляющую, то пределы допускаемой
основной относи­тельной
погрешности устанавливают по формуле

.
(3.5)

Так
обозначают классы точности мостов
переменного тока, счетчиков
электроэнергии, делителей напряжения,
измеритель­ных
трансформаторов и др.

• Если
СИ имеют как мультипликативную, так и
аддитивную

составляющие,
то класс точности обозначается двумя
цифрами, соответствующими
значениям с
и
d
формулы:

.
(3.6)

Здесь
с и d
выражаются также через ряд (3.4). Причем,
как правило,
с>d.
Например,
класс точности 0,02/0,01, означает, что
с
= 0,02, а d=0,01,
т. е. приведенное значение относительной
по­грешности
к началу диапазона измерения γ_n=
0,02%, а к концу γ_k
=0,01%.

Кроме
того, ГОСТ 22261—94 устанавливает пределы
допуска­емой
основной погрешности в виде относительной
погрешности, выраженной в децибелах
(дБ):

,

где
A’=
10 при измерении энергетических величин
(мощности, энергии,
плотности энергии);
А’= 20
при измерении силовых элекгромагшггных
величин (напряжения, силы тока,
напряженности поля).
Следует иметь в виду, что если два прибора
имеют разные чувствительности
S₁=
-100 дБ/Вт и .S₂=
-95 дБ/Вт, то значение чувствительности
у второго СИ выше, чем у первого, так как
-95>
-100.

Наиболее
широкое распространение (особенно для
аналого­вых
СИ) получило нормирование класса точности
по приведенной
погрешности:

^, (3.7)

Условное
обозначение класса точности в этом
случае зависит от
нормирующего значения х_N
,
т.
е. от шкалы СИ.

Если
х_N
представляется
в единицах измеряемой величины, то класс
точности обозначается числом, совпадающим
с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 оз­начает,
что γ = 1,5%.

Если
х_N
— длина
шкалы (например, у амперметров), то класс
1,5
означает, что γ =1,5% длины шкалы.

Не
всегда число, обозначающее класс
точности, показывает предел
допускаемой погрешности. В частности,
у некоторых одно­значных
мер электрических величин оно характеризует
нестабиль­ность,
показывая, на сколько процентов значение
меры может изменяться
в течение года.

Сравнения
способов выражения погрешностей
позволяют выс­казать
некоторые соображения.

При
известных классе точности СИ, выраженном
через при­веденную
погрешность γ, и чувствительности S
абсолютная по­грешность СИ составит

,
а
относительная на отметке x
соответственно,

.

Сравнение
формул (3.6) и (3.7) показывает, что первая
отра­жает
гиперболическую, а вторая — линейную
зависимость. При форме
записи (3.6) абсолютная погрешность имеет
вид:

.

Если
х
> Зх₀,
то шкала становится резко нелинейной
и про­изводить
измерения на этом участке неудобно.
Целесообразно перейти
на другой диапазон измерения. Расчетные
коэффици­енты с и d
округляются
до принятых рядом (3.4), а соотноше­ние
их с классом точности по приведенной
погрешности у при­ведено
в табл. 3.2.

Отрицательное
влияние аддитивной составляющей
погрешно­сти заключается в том, что
она не позволяет использовать одно и
то же СИ для измерения как больших, так
и малых величин. По­этому на начальной
части шкалы СИ измерения, как правило,
недопустимы.

Из
формулы относительной погрешности δ =
Δ/х видно, что ее значение растет обратно
пропорционально х
и
изменяется по ги­перболе (рис. 3.8), т.
е. относительная погрешность равна
классу СИ δ₀
лишь на последней отметке шкалы (х
=
х_k).
При
х→0 вели­чина δ→∞. При уменьшении
измеряемой величины до значения х_min
относительная погрешность достигает
100%. Такое значение измеряемой величины
называется порогом
чувствительности. Эта
величина ограничивает снизу полный
диапазон Д_п
измеряемых величин. Верхняя граница Д_п
ограничена пределом измерения х_к.

Отношение
Д_п
= x_k/
x_min
называют
еще полным динамическим диапазоном
измерения.

Тогда,
задаваясь некоторым значением
относительной погреш­ности δ_з
(например δ₃
= 5, 10 и 20%), можно ограничить снизу рабочий
диапазон Д_р
(рис. 3.8), т.е. величина Д_р
назначается доста­точно произвольно.

Резюмируя
изложенное, следует сказать, что если
класс точ­ности СИ установлен по
наибольшему допускаемому приведен­ному
значению погрешности (формула (3.7), а для
оценки по­грешности конкретного
измерения необходимо знать значение
аб­солютной или относительной
погрешности в данной точке, то в этом
случае выбор СИ, например, класс 1 (γ =
1%) для измере­ния с относительной
погрешностью ±1% будет правильный, если
верхний предел х_N
СИ
равен измеряемому значению х
величины.
В остальных случаях относительную
погрешность измерения необ­ходимо
определять по формуле

.
(3.8)

Таким
образом, снять показание — не значит
измерить. Надо оценить еще и погрешность
измерения, учитывая, что случайные
погрешности делают результат ненадежным,
а систематические — неверным. Допускаемая
величина относительной погрешности СИ
определяется требуемой точностью δ_изм
измерений. Постоянство ве­роятности
получения наибольшей возможной абсолютной
погреш­ности во всех точках шкалы
следует из формулы (3.8). Обычно от­носительная
погрешность в пределах рабочего участка
шкалы не может превышать приведенную
погрешность более чем в три раза.
Выполнение этого условия по отношению
к СИ с равномерной шкалой приводит к
тому, что при односторонней шкале рабочий
диапазон Д_р
занимает последние две трети ее длины
(рис. 3.9, а),
при
двусторонней шкале того же диапазона
— одну треть (рис. 3.9,6),
при
безнулевой шкале Д может распространяться
на всю длину шкалы (рис. 3.9, а),
т.е.
нерабочая зона шкалы L_нэ=
0.

Для некоторых СИ
характерна сложная зависимость
относи­тельной погрешности от
измеряемой величины или влияющих
фак­торов, которая приводит к
логарифмической характеристике
точ­ности. В основном это широкодиапазонные
СИ, например мосты постоянного тока,
мосты сопротивлений, цифровые частотоме­ры
и т. п. Для них ГОСТ 8.401—80 допускает
нормирование клас­сов точности
трехчленной формулой

,
(3.9)

где
х_min
и х_к
— порог
и предел чувствительности; δ_з
— относительная .
погрешность,
ограничивающая снизу рабочий диапазон,
в обозначениях рис. 3.8.

Например,
у широкодиапазонного моста сопротивлений
в тех­нической
документации указано, что относительная
погрешность не
превосходит значений в диапазонах:

10²,…,10⁴
Ом — 0,5 %; 5,…10⁵
Ом – 1 %;

0,5,…,10⁶
Ом – 5 %; 0,2,…,2∙10⁶
Ом – 10 % и 0,1,…,4∙10^б
Ом – 20 %.

При
δ_з
=0,5 %, х_min
=
0,02 Ом и х_к
= 20∙10⁶
Ом для любого х
относительная
погрешность составит

.

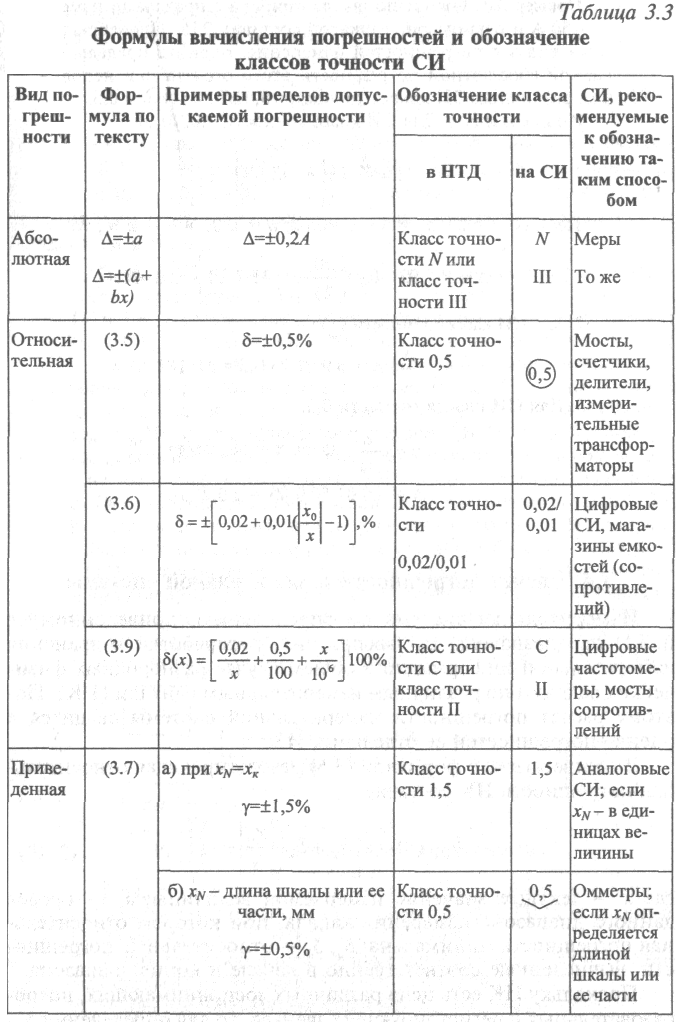
Обозначения
классов точности в документах и на
приборах приведены
в табл. 3.3.

3.5. Метрологические
характеристики цифровых средств
измерений

3.5.1. Общие положения

Под
цифровыми СИ (ЦСИ) будем понимать приборы,
пре­дусматривающие
либо цифровой отсчет показаний, либо
цифровое
преобразование измерительной информации:
ЦИУ (ЦИП) — цифровые
измерительные устройства (приборы); ИВК
— инфор­мационные вычислительные
комплексы; АЦП — аналого-цифро­вые
измерительные преобразователи; ЦАИ —
цифроаналоговые измерительные
преобразователи. Комплекс нормируемых
метро­логических
характеристик (НМХ) ЦСИ устанавливается
исходя из
их назначения. Если они относятся к СИ,
то в основу должны быть
положены ГОСТ 8.009-84, ГОСТ 8.401-80, РД
50-453-84. Если
ЦСИ выступает как средство автоматики,
то используют другие
стандарты.

Для
большинства ЦСИ характерно линейное
преобразование измеряемой
величины, т. е. показание ЦСИ пропорционально
чис­ловому
значению измеряемой величины или ее
отклонению от заданного
(например) значения. Различают
однопредельные, мно­гопредельные
и комбинированные ЦСИ для прямых,
косвенных или совокупных измерений.

Обобщенная
структурная схема ЦСИ (рис. 3.11) включает
ана­логовый
преобразователь (АП) входной величины,
квантователь (КВ),
преобразователь (ПК) и отсчетное
устройство (ОУ).

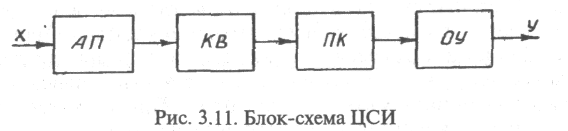
Для
упрощения на схеме (см. рис. 3.11) не показаны
блоки син­хронизации,
управления, памяти и другие блоки и
устройства, не­обходимые для обеспечения
заданного качества работы ЦСИ. От­метим
лишь, что квантователь осуществляет
квантование входного аналогового
сигнала по уровню (или по времени). В
общем случае ЦСИ
производит над измеряемой величиной
три операции — кван­тование
по уровню, дискретизацию времени и
кодирование. Сущ­ность квантования
по уровню заключается в том, что
бесконечно­му
множеству точек сигнала х_ВХ
в
рассматриваемом диапазоне от х_н
(нижнее)
до х_в
(верхнее
значение) ставится в соответствие
конеч­ное
и счетное множество выходных кодов
(квантов) [8; 55].

Дискретизация
по времени заключается в том, что
измерение производится
периодически (дискретно) в моменты
времени, за­даваемые,
например, генератором цикла. Интервал
времени от момента
подачи входного сигнала до момента
получения кодов называется
временем цикла.

Принцип
действия ЦСИ определяется принципом
действия его
квантователя: время-импульсное ЦСИ
имеет квантователь ин­тервала
времени; частотно-импульсное ЦСИ имеет
квантователь частоты;
кодо-импульсное (или поразрядного
уравновешивателя) ЦСИ
содержит квантователь постоянного тока
или напряжения. Встречаются и комбинации
квантователей.

В общем случае
показание отсчетного устройства ЦСИ

,
(3.12)

где
q
— шаг
(квант, ступень) квантования в единицах
измеряе­мой
величины.

Константа
q
—
важнейшая метрологическая характеристика
ЦСИ, устанавливающая
связь между измеряемой величиной х
и
выходным кодом
и определяющая чувствительность ЦСИ
(S=
1/q).

Величину
q
называют
еще номинальной ценой единицы наи­меньшего
(младшего) разряда кода. Обычно

q=k10^m,

где
k
=1, 2 или 5; т
—
любое целое число (положительное или
отрицательное)
или нуль.

Такое
название связано с тем, что обычно при
k
= 1
размер номинальной
ступени квантования q
= μ, где μ— цена единицы наименьшего
(младшего) разряда выходного кода N.
Например,
при
k
= 2 в
младшем десятичном разряде числа,
выражающего ре­зультат
измерения, индицируются только четные
цифры и нуль. Если
k
=5 —
индицируются только 0 или 5. При 1с
=5 квант
в 5 раз больше
значения единицы младшего разряда (q=
5μ).

В любом
ЦСИ СИ предусмотрено определенное
количество десятичных
разрядов, каждый из которых реализует
возможные состояния
входного сигнала, соответствующие
цифрам от 0 до 9. Тогда
максимальное число N_mах,
которое может индицироваться на ОУ, при
трех разрядах составляет 999, при четырех
— 9999 и т.д.
По аналогии со стрелочными СИ число
N_mах
называют
длиной цифровой шкалы.

Количество
квантов N
совпадает
с N_mах
при
k=
1.
В общем слу­чае
N_q
= N_mах
/k:
и число N_q
называют
разрешающей способностью ЦСИ,
которую обозначают как отношение,
например, 1:999.

Величина
N_mах
определяется разрядностью ЦСИ и при
полном использовании
старшего разряда

,

где
с
— основание
системы счисления; п
— число
разрядов. На­пример,
при с= 10 и n=
4,

N_mах
=
10 000 — 1 = 9999.

При
заданной верхней границе x_mах
диапазона измерений

.

При
анализе погрешностей измерения ЦСИ
рассматривают два
режима — статический и динамический.

Погрешность
измерения в динамическом режиме зависит
не только от свойств ЦСИ, но и от свойств
измеряемого сигнала, например
частотного спектра изменений x_вх,
подаваемого
на ЦСИ. Поэтому
для описания влияния динамических
свойств ЦСИ на погрешность измерения
в динамическом режиме понятие дина­мической
погрешности не используют, а рассматривают
только динамические
характеристики самого ЦСИ, в частности
его пе­реходную
характеристику.

3.5.2.
Статические погрешности цифровых
средств измерений

Основная
метрологическая характеристика линейного
ЦСИ — номинальная
функция преобразования

у
= k_Sх
(3.13)

или

y=y_min+k_Sx,
(3.14)

где
k_S
= const
— номинальный коэффициент преобразования.

Ступенчатая
линия рис. 3.12 описывается формулой,
соответ­ствующей
(3.13):

,
(3.15)

а рис. 3.13 — формулой,
соответствующей уравнению (3.14):

,
(3.16)

где
Lnt[А]
означает
«целая часть А»; signА
—
функция числа А
(signА
=
1 при А>0
и
sign
А=-1
при A<0).

Почти
все ЦСИ выполняют так, что k_S
=1, и в идеальном случае
функция ЦСИ (3.15) или (3.16) стремится к
идеальной функции
преобразования аналогового СИ у
=k:

.
(3.17)

Поскольку
у ЦСИ, как квантователя, всегда q≠0,
то
даже идеальные ЦСИ обладают погрешностью,
обусловленной нали­чием
q.

Как
и для аналоговых СИ, в случае ЦСИ основная
статическая погрешность
Δ есть сумма систематической и случайной
составля­ющих
(Δ = Δ_C
+Δº). Для раскрытия их структуры рассмотрим
две составляющие
погрешности ЦСИ: методическую,
обусловленную принципом
аналого-цифрового преобразования, и
инструментальную,
обусловленную конструкцией и свойствами
реальных элемен­тов
схемы ЦСИ. В литературе [4; 6] встречаются
еще понятия погрешности
нелинейности или дифференциальной
линейности. Од­нако
величина этой погрешности в условиях
эксплуатации ЦСИ весьма
мала и представляет интерес лишь для
разработки ЦСИ.

В
аналоговых СИ числовое значение
результата измерения оп­ределяет
оператор (снимает показания, производит
округление и записывает
результат полученных чисел значащих
цифр). При этом возникает
субъективная ошибка определения.

В
ЦСИ операция округления производится
самим СИ, и ошиб­ка
этой операции относится к методической
погрешности. Одно­временно
с округлением ЦСИ осуществляет квантование
сигнала путем сравнения его с определенным
уровнем. Таким образом, ли­нейное ЦСИ
есть квантователь непрерывной измеряемой
величи­ны,
и его номинальная характеристика
преобразования имеет вид:

,

где
N
— значение
выходной величины ЦСИ (целое число); х
— значение
измеряемой величины.

При
квантовании число N
должно
быть таким, чтобы выпол­нялось
неравенство

,

означающее,
что любое значение х,
попавшее
в этот интервал, округляется
до значения N.

Абсолютная
погрешность квантования, приведенная
ко вхо­ду,
составит

,

а
к выходу
.

Графически
функция Δ_к
=f(х)
приведена на рис. 3.14, а.
По­скольку
х
— величина
случайная, то и Δ_к
— тоже случайная вели­чина,
как правило, с равномерным законом
распределения (рис. 3.14,
б).
Погрешность
квантования является центрированной
(с ма­тематическим
ожиданием, равным нулю) случайной
величиной. Предельное значение ее [Δ_к]
=0,5q,
и СКО:

.

Погрешность
квантования является аддитивной
погрешностью, так
как абсолютное ее значение не зависит
от того, в какой части диапазона находится
х.
Погрешность
квантования контролю не подлежит.

Относительная
погрешность квантования

,

а приведенная
погрешность квантования

.

Отсюда
можно получить выражение для определения
необхо­димого
числа разрядов

.

Например,
для ЦСИ с десятичным отсчетом при γ_к
= 0,5; 0,05 и 0,005 % необходимо иметь соответственно
2, 3 и 4 десятичных разряда,
а для двоичного ЦСИ — 7 (2⁷=
128), 10 (2¹⁴=
1024) и 14
(2^й
= 16384) двоичных разрядов.

Для
частотно-импульсных ЦСИ, т.е. измеряющих
частоту, вре­мя,
фазу и т.п., характерна погрешность
несинхронизации, так­же
относящаяся к методическим. В таких СИ
результат измерения N
получают
подсчетом числа импульсов периодического
сигнала за
интервал времени. При измерении интервала
времени T_x
образцовой является частота f₀
импульсов, а при измерении частоты f₀
, образцовым является интервал времени
Т₀
(рис.
3.15).

Время
несинхронизации t_к
— это время между моментами, соответствующими
началу интервала и переднему фронту
одного (очередного) из счетных импульсов.
Очевидно, при измерении Т_к
это
время находится в пределах

,
а при измерении часто­ты
f_x—

.

Синхронизация
в цифровых СИ может быть организована
по-разному.
Если она вообще не предусмотрена, то t_н
— случайное
время, а следовательно, и погрешность
несинхронизации — слу­чайная
величина. Введением синхронизации эта
погрешность либо исключается,
либо становится систематической.

При
измерении интервала времени Т_х
функция
преобразова­ния
ЦСИ

Поскольку
в таких СИ
q=1/f₀=
Т₀,
то

.

Очевидно,
что если время t_н
=
0,5 Т₀,
то
погрешность несинх­ронизации Δ_t=
0 и методическая погрешность будут иметь
только одну
составляющую — погрешность квантования
(см. рис. 3.14, а).

При
синхронизации без задержки t_н=
0 и Δ_t
= -0,5q=
-0,5T₀.
В этом
случае методическая погрешность Δ_м
= Δ_к
+Δ_t,
(рис. 3.16, а)
с равномерной
плотностью

распределения (рис. 3.16,
б).

При
отсутствии синхронизации время t_н
и
погрешность Δ_к
ста­новятся
случайными величинами.

Поскольку
t_н
— случайная величина с равномерной
плотнос­тью и погрешность квантований
t_к
— тоже
случайная величина с равномерной
плотностью, то их композиция дает
треугольный закон
(закон Симпсона) с предельным значением
погрешности Δ_м
= q
и
СКО σ_t
= 0,41q.

При
цифровом измерении частоты f_x

.

Так
как q=
1/Т₀
(Т₀
— предел
образцовой частоты f₀),
то

.

Для
обеспечения округления необходимо
вводить задержку при синхронизации
на значение t_н
= 0,5T_x.
Если в СИ предусмотрена такая
регулируемая задержка, то Δt
= 0.

При
синхронизации (когда t_н=
0) показание, например, частотомера
может быть только заниженным, а погрешность
Δt=-0.5q=-0.5/T₀
является
систематической. Методическая погрешность
показана
на рис. 3.16.

При
отсутствии синхронизации возникает
случайная погреш­ность
несинхронизации Δ_г
и методическая погрешность будет иметь
вид
(см. рис. 3.17,6).

Поскольку
погрешности квантования и синхронизации
при­сущи
принципу работы цифрового СИ, то они
отнесены к разря­ду
методических, а не инструментальных.

Для
оценки инструментальной погрешности
ЦСИ разобьем шкалу
идеального линейного квантования на
строки, равные но­минальному
значению q
(верхняя
часть рис. 3.18, а).
Цифровому
значению
соответствует некоторая область (так
как реально число округляется) значений
измеряемой величины х.
Эта
область нахо­дится между уровнями
(h-0,5)q
и (h+0,5)q.
Считаем, что h-й
точке
квантованной шкалы соответствует
значение измеряемой величины, равное
(h
+ 0,5)q.

В
реальном квантователе (нижняя часть
рис. 3.18, а)
значения
ступеней
квантования могут не только отличаться
от номиналь­ного
д,
но
и быть неравными между собой. Тогда
действительные значения
уровня h-й
точки шкалы (рис. 3.18, б):

,

где
q₀,,q_i
— действительные
значения ступеней квантования в точках
0
и i
соответственно.

Таким
образом, разность между действительным
и номиналь­ным значениями рассмотренных
уравнений есть инструменталь­ная
погрешность

. (3.18)

Графическая
интерпретация суммирования методической
и ин­струментальной
погрешностей ЦСИ приведена на рис.
3.19,а, а функции
погрешности — на рис. 3.19,5.

Составляющая
погрешности из-за квантования
пренебрежительно мала,
если предел допускаемой основной
погрешности (Δ_ор/q)>3,3.

Для
сравнения следует принять во внимание,
что при ис­пользовании
аналоговых приборов квантование по
уровню про­исходит
при считывании показаний оператором.
Считывание по­казаний
производится с погрешностью 0,2—0,3 от
предела до­пускаемой
основной погрешности. Поэтому при
Δ_ор>(3-5)q
метрологическое
различие между аналоговым и цифровым
СИ стирается.

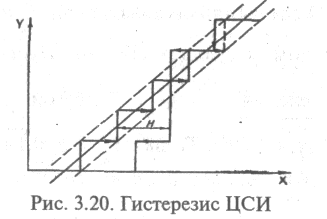
При
оценке инструментальной составляющей
возможна вариа­ция
Н
показаний
ЦСИ при подходе к заданной точке х
«снизу»
и «сверху».
Эта вариация обусловлена наличием в
конструкциях ЦСИ релейных
элементов (реле, компараторов, усилителей
и т.п.), да­ющих остаточные сигналы в
виде гистерезиса. Поэтому для ЦСИ
вариацию
показаний принято называть погрешностью

гисте­резиса
H
(рис. 3.20). Тогда составляющая статическая
систематическая
погрешность Δ_ст
принимается равной в реальном ЦСИ
си­стематической
составляющей его инструментальной
погрешнос­ти,
выраженной через вариацию со СКО σ_н
= 0,29H
по формуле

.

Вариация
учитывается лишь в случае, если H²>0,1q²
или
H_ор>0,62q.

Случайная
составляющая основной статической
погрешности

,

или

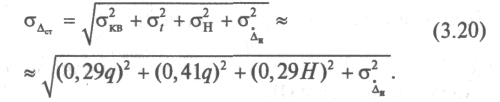
Величину
СКО случайной составляющей


инструментальной
погрешности
находим следующим образом. Пусть при
нормальном законе
ее распределения

.
С другой стороны, известно,
что

.
Тогда

,
откуда

=0,1q.

Таким образом, по
формуле (3.20) определяем

.

Вообще случайная
составляющая учитывается, если

или

>0.18q.

Тогда
окончательно интервал, в котором с
заданной вероятнос­тью
Р
находится
основная статическая погрешност Δ_ст
ЦСИ, оп­ределяется
неравенством

,
(3-21)

Соответственно
для Р=
0,99;
0,95 и 0,90 коэффициент К=
2,57;
1,96
и 1,65.

В
качестве примера рассмотрим оценку
погрешности аналого-цифрового
преобразователя, используемого при
виброакустичес­кой диагностике. Среди
АЦП можно выделить: погрешность
кван­тования; погрешность смещения
нуля; погрешность коэффициента передачи;
погрешность, вызываемую нелинейностью
характерис­тики
квантования; температурную погрешность.

Из
динамических погрешностей следует
учитывать погрешно­сти,
обусловленные частотой дискретизации
и апертурным вре­менем
— интервалом временной неопределенности
задержки мо­мента
отсчета.

Результирующая
погрешность Δ_Σ
АЦП представляет собой сумму
статических
(Δ_ст)
и динамических (Δ_g
) погрешностей

а ее дисперсия
равна

.

Шаг квантования
определяется как

,

где
х_max,,
х_min
— максимальная и минимальная амплитуды
сигнала; п
—
число разрядов АЦП.

Погрешность
квантования с равномерным шагом
принимает­ся равной Δ_к
= q/2.

Энергетический
спектр шума квантования в интервале
частот входного
сигнала 0,…,f.
определяется по формуле

0<f<f_i.

где
f_i—
частота дискретизации.

Основными
компонентами результирующей статической
по­грешности
являются высокочастотная и низкочастотная
компо­ненты.
Высокочастотной компонентой является
центрированная составляющая
результирующей погрешности,
характеризующая­ся
взаимонезависимыми значениями.
Низкочастотной компонен­той
является математическое ожидание
результирующей погреш­ности
с высокой степенью корреляции ее значений
между собой.

Основной
характеристикой высокочастотной
погрешности является
ее СКО а, а низкочастотная погрешность
Δ — функцией параметров
входного вибросигнала х
и
внешних возмущений W.

Оценка
значений Δ и σ в каждой точке пространства
сигнала и
воздействий
производится по формулам:

,

где
М — математическое ожидание приведенной
ко входу АЦП результирующей погрешности;
х₀
—
образцовое значение преоб­разуемого
вибросигнала; Y_j(j=
1, 2,…, т)
— выборка
значений вы­ходной
координаты АЦП при входном сигнале х.

Погрешность
δ_x
установки значения х₀
прецизионным АЦП должна
удовлетворять условию

Δ
>>
δ_x
.

Искомое
значение Δ в данной точке пространства
аргументов x,
ω со находится как среднее значение Δ_i
по всем i-м
точкам

Числовые
значения параметров δ_x,
σ₀
и т
устанавливаются
в стандартах или технических условиях
на конкретные типы АЦП.

Приведенное
значение дисперсии результирующей
погрешно­сти
АЦП с равномерной шкалой квантования
для случайного сиг­нала
с нормальным распределением спектра
при М =0 определя­ют
по формуле

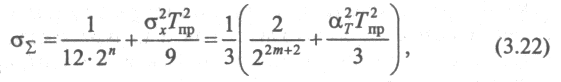
где

— дисперсия производной процесса;
R_х(τ)—
вто­рая
производная корреляционной функции
процесса x(t);
T_пр
— время
преобразования;

где
F_max
—
максимальная частота входного сигнала.

При
неизвестной корреляционной функции
значение диспер­сии
динамической погрешности АЦП для
вибросигнала с нор­мальным
распределением определяется по формуле

Значение
дисперсий динамической погрешности
для случай­ного сигнала с равномерным
распределением следует определять как

Максимальная
величина погрешности датирования равна

где
t_АП
— апертурное
время.

В
худшем случае инструментальная
погрешность допускается равной
погрешности квантования. Основные
параметры АЦП долж­ны
выбираться с учетом статистических
свойств входного вибро­сигнала
в соответствии с частными техническими
условиями на конкретные
типы преобразователей.

Для
вибросигнала, имеющего нормальное
распределение и корреляционную функцию
вида:

где
σ_x
— дисперсия
входного вибросигнала, выполняется
условие:

,

где
а — время преобразования для одного
разряда (быстродей­ствие);
п
—
число разрядов.

Параметры
выходных сигналов АЦП должны соответствовать
требованиям
ГОСТ 26.201.−94.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Класс точности СИ — обобщенная характеристика средств измерений, определяемая пределами допускаемых основной и дополнительной погрешностей, а также другими свойствами средств измерений, влияющими на их точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.

• Классы точности присваиваются средствам измерений при их разработке (по результатам приемочных испытаний). В связи с тем что при эксплуатации их метрологические характеристики обычно ухудшаются, допускается понижать класс точности по результатам поверки (калибровки). Таким образом, класс точности позволяет судить о том, в каких пределах находится погрешность измерений этого класса. Это важно знать при выборе СИ в зависимости от заданной точности измерений.

• Классы точности конкретного типа СИ устанавливают в НД. При этом для каждого класса точности устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающим уровень точности СИ данного класса. эталон единицы величины — техническое средство, предназначенное для воспроизведения, хранения и передачи единицы величины.

• Средствам измерений с двумя или более диапазонами измерений одной и той же физической величены допускается присваивать два или более класса точности. Средствам измерений, предназначенным для измерений двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины. С целью ограничения номенклатуры средтсв измерений по точности для СИ конкретного вида устанавливают ограниченное число классов точности, определяемое технико-экономическими обоснованиями.
• Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнительной обработки результатов измерений устанавливают без учета режима обработки.

Способы нормирования и формы выражения метрологических характеристик

Пределы допускаемых основной и дополнительных погрешностей следует выражать в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида. Пределы допускаемой дополнительной погрешности допускается выражать в форме, отличной от формы выражения пределов допускаемой основной погрешности.

Пределы допускаемой основной погрешности устанавливают в последовательности, приведенной ниже:

Устанавливаются пределы допускаемой абсолютной погрешности по формуле: 

Δ = ± а или Δ = ± (а + b·x)

• где Δ — пределы допускаемой абсолютной основной погрешности (в единицах измеряемой величины или условно в делениях шкалы)

• х — значение измеряемой величины,
  а, b — положительные числа, не зависящие от х.

Устанавливаются пределы допускаемой приведенной основной погрешности по формуле:

 γ = Δ / Хn = ± p

• где γ — пределы допускаемой приведенной основной погрешности в %,

• Δ — пределы допускаемой абсолютной погрешности,

• p — положительное число, выбираемое из ряда 1·10ⁿ, 1,5·10ⁿ, (1,6·10ⁿ)*, 2·10ⁿ,  2,5·10ⁿ, (3·10ⁿ)*, 4·10ⁿ, 5·10ⁿ, 6·10ⁿ (n = 1, 0, -1, -2 и т.д.)

  *не устанавливается для вновь разрабатываемых средств измерений,
  для средств измерений конкретного типа допускается устанавливать не более пяти различных пределов допускаемой основной погрешности при одном и том же значении степени n.

Устанавливается нормируещее занчение Хn

• Для средств измерений с равномерной, практически равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение измеряемого параметра находся на краю или вне диапазона измерений нормирующее значение устанавливается равным большему из пределов измерений. Для средств измерений, нулевое значение измеряемого параметра которых находится внутри диапазона измерений, нормирующее значение устанавливается раным большему из модулей пределов измерений.
• Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.
• Для средств измерений физической величины, для которых принята шкала с условным нулем, нормирующее значение устанавливают равным модулю разности пределов измереинй.
• Для средств измерений с установленным номинальным значением нормирующее значение устанавливают равным этому номинальному значению.
• Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным всей длине шкалы или её части, соответствующей диапазону измерений. В этом случае пределы абсолюной погрешности выражают, как и длину шкалы, в единицах длины.

Устанавливаются пределы допускаемой относительной основной погрешности по формуле:

δ = Δ / х = ± [c + d·(|х_к / х| — 1)] =<  ± q

• где с = b + d;  d = a / |х_к|
  δ — пределы допускаемой относительной основной погрешности в %,
  Δ — пределы допускаемой абсолютной основной погрешности (в единицах измеряемой величины или условно в делениях шкалы)
  х — значение измеряемой величины,
  х_к — наибольший (по модулю) из пределов измерений,
  а, b — положительные числа, не зависящие от х.
  q, c, d — положительное число, выбираемое из ряда 1·10ⁿ, 1,5·10ⁿ, (1,6·10ⁿ)*, 2·10ⁿ,  2,5·10ⁿ, (3·10ⁿ)*, 4·10ⁿ, 5·10ⁿ, 6·10ⁿ (n = 1, 0, -1, -2 и т.д.)
  *не устанавливается для вновь разрабатываемых средств измерений,
  для средств измерений конкретного типа допускается устанавливать не более пяти различных пределов допускаемой основной погрешности при одном и том же значении степени n.
  В обоснованных случаях пределы допускаемой относительной оснвоной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.
  В стандартах или технических условиях на средтсва измерений должно быть установлено минимальное значение х, начиная от которого применим принятый способ выражения пределов допускаемой относительной погрешности.
  Соотношение между числами с и d устанавливаются в стандартах на средства измерений конкретного вида.

Пределы допускаемых дополнительных погрешностей устанавливают одним из следующих способов:

• • в виде постоянного значения для всей рабочей области влияю-щей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;
  • путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;
  • путем указания зависимости предела допускаемой дополнительной погрешности от влияющей величины (предельной функции влияния);
  • путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.
• Для различных условий эксплуатации средств измерений в рамках одного и того же класса точности допускается устанавливать различные рабочие области влияющих величин.
• Предел допускаемой вариации выходного сигнала следует устанавливать в виде дольного (кратного) значения предела допускаемой основной погрешности или в делениях шкалы.
• Пределы допускаемой нестабильности, как правило, устанавливают в виде доли предела допускаемой основной погрешности.
• Пределы допускаемых погрешностей должны быть выражены не более чем двумя значащими цифрами, причем погрешность округления при вычислении пределов должна быть не более 5%.

Обозначение классов точности средств измерений в документации :

• Для средств измерений пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей или относительных погрешностей, причем последние установлены в виде графика, таблицы или формулы, классы точности в документации обозначаются прописными буквами латинского алфавита или римскими цифрами.
• В необходимых случаях к обозначению класса точности буквами латинского алфавита добавляют индексы в виде арабской цифры. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, соответствуют буквы, находящиеся ближе к началу алфавита, или цифры, означающие меньшие числа.
• Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме приведенной погрешности или относительной погрешности в соответствии с формулой δ = Δ / х  =  ± q, классы точности в документации следует обозначаются числами, которые равны этим пределам погрешности, выраженными в процентах. Обозначение класса точности таким образом, дает непосредственное указание на предел допускаемой основной погрешности.
• Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей в соответствии с формулой δ = ± [c + d·(|х_к / х| — 1)], классы точности в документации обозначаются числами с и d, разделенных косой чертой.

• В документации на средства измерений допускается обозначать классы точности так же, как на средтсвах измерений.

• В эксплуатационной документации на средство измерений конкретного вида, содержащей обозначение класса точности, содержится ссылка на стандарт или технические условия, в которых установлен класс точности этого средства измерений.

Обозначение классов точности на средствах измерений :

• Условные обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений.

• При указании классов точности на измерительных приборах с существенно неравномерной шкалой, для информации, дополнительно указываются пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками (например точками или треугольниками). К значению предела допускаемой относительной погрешности в этом случае добавляют знак процента и помещают в кружок. Обращаем ваше внимание на то, что этот знак не является обозначением класса точности.

• Обозначение класса точности допускается не наносить на высокоточные меры, а также на средства измерений, для которых действующими стандартами установлены особые внешние признаки, зависящие от класса точности, например параллелепипедная и шестигранная форма гирь общего назначения.

• За исключением технически обоснованных случаев, вместе с условным обозначением класса точности на циферблат, щиток или корпус средств измерений наносится обозначение стандарта или технических условий, устанавливающих технические требования к этим средствам измерений.

• На средства измерений, для одного и того же класса точности которых в зависимости от условий эксплуатации установлены различные рабочие области влияющих величин, наносятся обозначения условий их эксплуатации, предусмотренные в стандартах или технических условиях на эти средства измерений.

Расшифровка обозначений классов точности на средствах измерений :

Обозначение класса точности	Форма выражения погрешности	Пределы допускаемой основной погрешности	Примечание
на средстве измерений	в документации
0,5	Класс точности 0,5	Приведенная	γ = ±0,5%	нормирующее значение выражено в единицах измеряемой величины
	Класс точности 0,5	γ = ±0,5%	нормирующее значение принято равным длине шкалы или её части
	Класс точности 0,5	Относительная	δ = ±0,5%	δ = Δ / х
0,02/0,01	Класс точности 0,02/0,01	δ = ±[0,02 + 0,01·(|хк / х| — 1)] %	δ = ±[c + d·(|хк / х| — 1)]

Класс точности хотя и характеризует совокупность метрологических свойств данного средства измерений, однако не определяет однозначно точность измерений, так как последняя зависит от метода измерений и условий их выполнения.

В 20.05.2020 в 10:57, Pan 77 сказал:

А формулу расчета приведенной погрешности взял оттуда же, из ГОСТ 8.401-80 (п. 2.3.2). Только не знаю, правильно ли я взял ХN  равным 2%?

Что касается приведенной погрешности, если вы внимательно прочитаете этот пункт ГОСТа, то вы поймете, что там ХN в принципе не может быть в процентах, т.к.
 — пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);
 — нормирующее значение, выраженное в тех же единицах, что и ;

Еще раз ХN это нормирующее значение (как правило верхний предел измерения СИ), а не погрешность чего-либо.

В 20.05.2020 в 10:57, Pan 77 сказал:

И сравнивать в последнем предложении нужно было не с 0,102 а с 2%?

Если честно непонятно, почему вы все усложняете, вот вы пишете

В 18.05.2020 в 17:21, Pan 77 сказал:

Например. В ГОСТ на испытания фигурирует газоанализатор с допустимой погрешностью ±2%.

И тут вопрос, в % может быть указана относительная погрешность и  приведенная — исходя из понимания какая, можно посчитать допустимую погрешность в абсолютных значениях в нужной вам точке диапазона. Вы рассчитываете исходя их того, что у вас погрешность относительная и для точки 250 мг/м3 получаете допустимую погрешность 5 мг/м3

И далее вы считаете

В 18.05.2020 в 17:21, Pan 77 сказал:

У нас в арсенале имеется газоанализатор ЭЛАН-СО-500 с допускаемой основной погрешностью, равной ± (0,5 + 0,1Сх), мг/м3 где Сх — измеренная концентрация. Беру, к примеру, половину шкалы = 250 мг/м3. Тогда, 

∆ = 0,5+(0,1*250) = 25,5 мг/м³ допускаемая абсолютная погрешность.

Ну очевидно, что если вам надо уложиться в 5 мг/м3, то 25,5 мг/м3 значительно больше, что тут еще сравнивать?