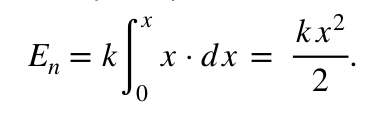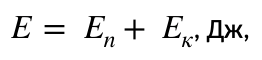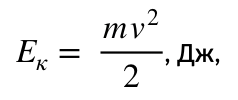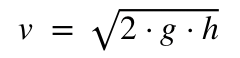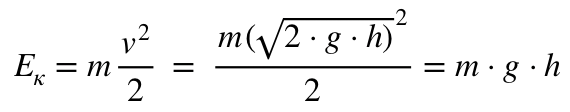Как найти кинетическую энергию тела на пружине

Рассмотрим процесс превращения энергии при колебательном движении идеального горизонтального пружинного маятника (рис. (1)).

Рис. (1). Колебания горизонтального пружинного маятника

Будем считать, что в системе сил трения и сил сопротивления нет.

Когда эта система находится в равновесии и никакого колебания не происходит, скорость тела равна нулю и отсутствует деформация пружины (рис. (2)) В этом случае энергии у данного маятника нет.

Рис. (2). Положение пружинного маятника в равновесии

Когда тело выводится из положения равновесия, например пружина сжимается на некоторую величину (рис. (3)) телу сообщается некоторый запас потенциальной энергии:

Рис. (3). Положение пружинного маятника при сжатой пружине

Если теперь отпустить груз, не удерживать его, то он начнёт своё движение к положению равновесия, пружина начнёт выпрямляться, и деформация пружины будет уменьшаться (рис. (4)) Следовательно, будет уменьшаться и её потенциальная энергия.

Скорость же тела будет увеличиваться, и по закону сохранения энергии потенциальная энергия пружины будет превращаться в кинетическую энергию движения тела:

Рис. (4). Движение груза к положению равновесия

В момент прохождения те­лом положения равновесия (рис. (5)) его по­тенциальная энергия равна нулю, а кинетическая будет максимальна.

Рис.(5). Прохождение грузом положения равновесия

Потом вступает в действие явление инерции. Тело, которое обладает некоторой массой, по инерции проходит точку равновесия (рис. (6)). Скорость тела начинает уменьшаться, а деформация, удлинение пружины, увеличивается. Следовательно, кине­тическая энергия тела убывает, а потенциальная, наоборот, возрастает.

Рис. (6). Положение пружинного маятника при удлинении пружины

В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна (рис. (7)).

Рис. (7). Положение пружинного маятника в точке максимального отклонения тела

Таким образом, при колебаниях периодически проис­ходит переход потенциальной энергии в кинетическую и обрат­но.

Рис. (8). Колебания вертикального пружинного маятника

Если для вертикального пружинного маятника выбрать систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю, то всё описанное выше для горизонтального маятника можно применить для данного маятника.

Во многих механизмах используется потенциальная и кинетическая энергия пружины. Их используют для выполнения различных действий. В отдельных узлах они фиксируют детали в определенном положении, не позволяя смещать в какую-либо сторону (барабан револьвера относительно корпуса). Другие пружинные системы возвращают исполнительный механизм в исходное положение (курок ручного огнестрельного оружия). Есть устройства, где узлы с гибкими свойствами совершают перемещения в устойчивое положение (механические стабилизаторы).

Работа связана с изменением геометрических параметров упругого тела. Прилагая нагрузку, заставляют эластичную деталь сжиматься (растягиваться или изгибаться). При этом наблюдается запасание энергии. Возвратное действие сопровождается набором скорости. Попутно возрастает кинетическая энергия.

Потенциальная энергия пружины

Рассматривая в качестве накопителя энергии пружину, следует отметить ее отличительные свойства от иных физических тел, которые могут накапливать энергетический потенциал. Традиционно понимается следующее: для накопления потенциала для последующего движения необходимо совершение движения в силовом поле:

Е_п = F ⋅ l, Дж (Н·м),

где Е_п– потенциальная энергия положения, Дж;
F – сила, действующая на тело, Н;
l – величина перемещения в силовом поле, м.

Энергия (работа) измеряются в Джоулях. Величина представляет произведение силы (Н) на величину перемещения (м).

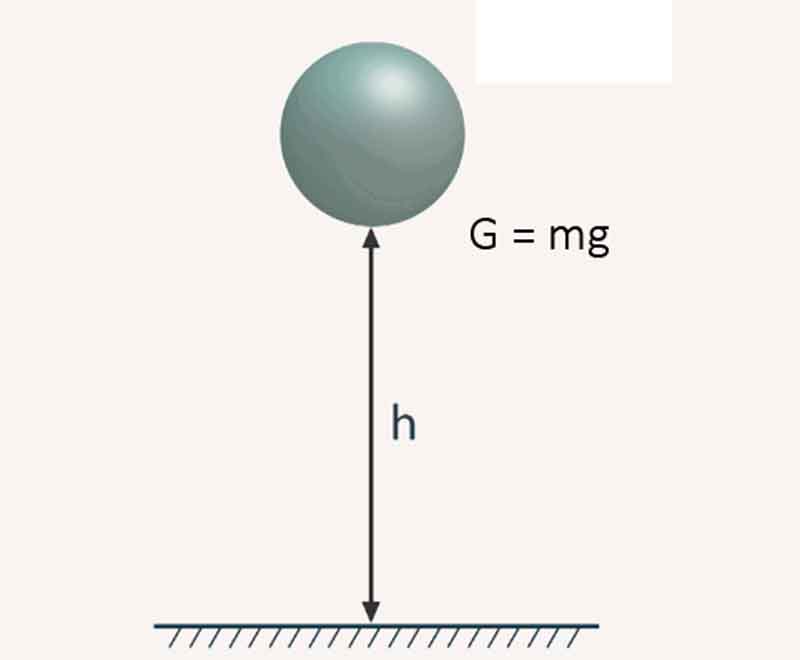
Если рассматривать условие в поле тяготения, то величина силы находится произведением ускорения свободного падения на массу. Здесь сила веса находится с учетом g:

Е_п = G ⋅ h = m ⋅ g ⋅ h, Дж

здесь G – вес тела, Н;
m – масса тела, кг;
g – ускорение свободного падения. На Земле эта величина составляет g = 9,81 м/с².

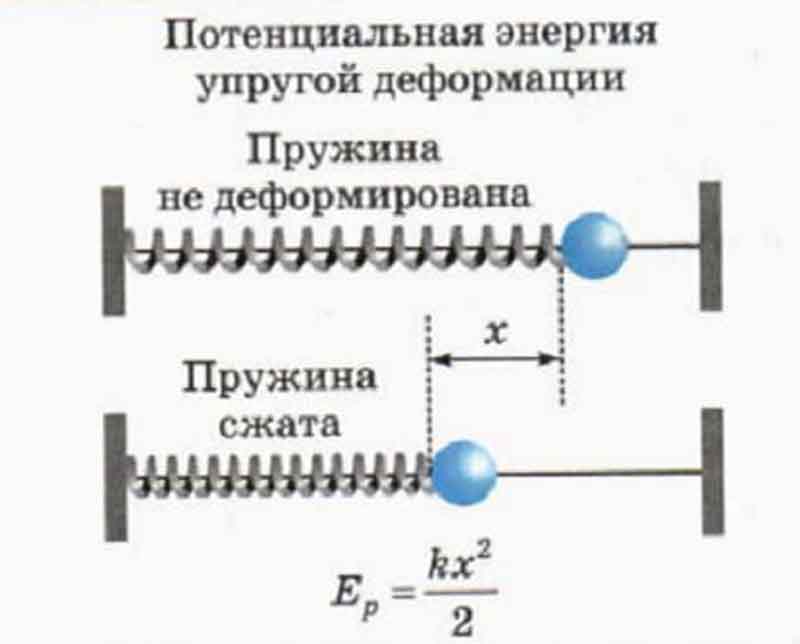
Если расстраивается пружина, то силу F нужно определять, как величину, пропорциональную перемещению:

F = K ⋅ x, Н,

где k – модуль упругости, Н/м;
х – перемещение при сжатии, м.

Величина сжатия может изменяться по величине, поэтому математики предложили анализировать подобные явления с помощью бесконечно малых величин (dx) .

При наличии непостоянной силы, зависящей от перемещения, дифференциальное уравнение запишется в виде:

dE_п = k ⋅ x ⋅ dx

здесь dE_п – элементарная работа, Дж;
dx – элементарное приращение сжатия, Н.

Интегральное уравнение на конечном перемещении запишется в виде. Ниже вывод формулы:

Пределами интегрирования является интервал от 0 до х. Деформированная пружина приобретает запас по энергетическим показателям

Окончательно формула для расчета величины потенциальной энергии сжатия (растягивания или изгиба) пружины запишется формулой:

Закон сохранения механической энергии

Закон сохранения энергии существует независимо от желания наблюдателя. Все физические законы имеют статистический характер: существуют только подтверждения их выполнения, нет ни одного адекватно выполненного опыта, при котором наблюдается нарушение этой закономерности. Природные явления только подтверждают сохранность работы и энергозатрат, затраченных на ее выполнение.

На основании изложенного сформулировано положение:

где Е_к – кинетическая энергия, Дж.

Рассматривая перемещения тела, наблюдаются изменения потенциальной и кинетической энергий. При этом сумма значений остается постоянной.

Проще всего проследить за изменениями между разными видами энергетических показателей при рассмотрении движения маятника.

Из крайнего положения (шарик на нити отклонился в одну из сторон, Еп = max) тело движется под действием силы тяжести. При этом снижается запасенная энергия. Движение сопровождается увеличением скорости. Поэтому нарастают показатели динамического перемещения Е_к.

В нижней точке не остается никаких запасенных эффектов от положения шарика. Он опустился да минимума. Теперь Е_к =max.

Поучается, при совершении гармонических колебаний маятник поочередно накапливает то один, то другой вид энергии. Механические превращения из одного вида в другой налицо.

Кинетическая энергия

Движущееся тело характеризуется скалярной величиной (масса) и векторная величина (скорость). Если рассматривать реальное перемещение в пространстве, то можно записать уравнение для определения кинетической энергии:

здесь v – скорость движения тела, м/с.

Использование кинетического преобразования можно наблюдать при колке орехов.

Приподняв камень повыше, далекие предки создавали необходимый потенциал для тяжелого тела.

Приподняв камень на максимальную высоту, разрешают ему свободно падать.

Двигаясь с высоты h, он набирает скорость

Поэтому в конце падения будет получена кинетическая энергия

Рассматривая входящие величины, можно увидеть, как происходит преобразование величин. В конце получается расчетная формула для определения потенциальной энергии.

Даже на уровне вывода зависимостей можно наблюдать выполнение закона сохранения энергии твердого тела.

Использование энергии пружины на практике

Явление преобразования потенциальной энергии пружины в кинетическую используется при стрельбе из лука.

Натягивая тетиву, стреле сообщается потенциал для последующего движения. Чем жестче лук, а также ход при натягивании тетивы, тем выше будет запасенная энергия. Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.

В результате стрела полетит в цель. Ее поражающие свойства определятся величиной кинетической энергии (mv²/2).

Для гашения колебаний, возникающих при движении автомобиля, используют амортизаторы. Основным элементом, воспринимающим вертикальную нагрузку, являются пружины. Они сжимаются, а потом возвращают энергию кузову. В результате заметно снижается ударное воздействие. Дополнительно устанавливается гидроцилиндр, он снижает скорость обратного движения.

Рассмотренные явления используют при проектировании механизмов и устройств для автоматизации процессов в разных отраслях промышленности.

Видео: закон Гука и энергия упругой деформации.

Republished by Blog Post Promoter

Формулы пружинного маятника в физике

Формулы пружинного маятника

Определение и формулы пружинного маятника

Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

[ddot{x}+{omega }^2_0x=0left(1right),]

где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

[T=2pi sqrt{frac{m}{k}}left(4right).]

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]

начальная фаза при этом:

[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

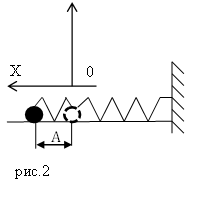
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

[E_p=-frac{dF}{dx}(8)]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]

Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]

где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Читать дальше: формулы равноускоренного прямолинейного движения.

Потенциальная и кинетическая сила – два довольно распространенных показателя, которые касаются не только пружины, но и многих других тел. Рассмотрим особенности кинетической подробнее.

Понятие энергии

Прежде чем рассматривать особенности пружины следует уделить внимание тому, что с ней происходит при сжатии, растяжении и каким образом она оказывает воздействие на тело, окружающую систему. Энергия – скалярная физическая величина, которая применяется для определения формы движения и взаимодействия материи. Важным моментом назовем то, что если система замкнутая, то усилие сохраняется на протяжении длительного периода. Сегодня она окружает нас практически везде и касается довольно большого количества объектов.

Довольно большое распространение получило понятие кинетическая энергия пружины. Она связано с непосредственными особенностями самого изделия. При воздействии определенного усилия на витки, расположенные вдоль одной спирали, формируется сила, которая может использоваться в качестве полезной работы.

Энергия кинетическая: формула и определение

Механическая система, которая связана со скоростью перемещения объекта, применяется крайне часто. Стоит учитывать, что она может делиться на поступательную и вращательную. В качестве единицы измерения используется джоуль.

Среди особенностей отметим нижеприведенные моменты:

1. Рассматриваемый тип усилия также представлен разностью между исходным состоянием тела и его положением в полном спокойствии.
2. Обуславливается возникновение определенного усилия, за счет которого обеспечивается перемещение тела и совершение работы.

Пружина за счет силы упругости приводит в движение различные объекты. При этом жесткость пружины растянутой может быть различной, все зависит от особенностей конкретного изделия.

Рассматриваемая формулу следует уделить внимание достаточно большому количеству различных моментов. Особенностями назовем следующее:

1. Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении. Кроме этого, уделяется внимание взаимному расположению витков.
2. Работа, которая может совершаться пружиной, зависит от взаимного положения частей тела. Начальное и конечное растяжение может существенно отличаться.
3. Рассматриваемое изделие в растянутом положении может совершать различную работу. Расчеты позволяют определить то, каково ее значение, а также величину потенциальной.

Расчеты могут проводится исключительно после создания схемы. Примером назовем следующее:

1. Один конец витков закреплен за основание, второй предназначен для совершения работы.
2. Не стоит забывать о том, что показатель изменяется, он не остается постоянным. Изменения пропорционально растяжению.
3. Изначальное растяжение обозначается буквой l, для определения первоначального значение силу упругости применяется формула F=kl. В данной формуле используется коэффициент k, который обозначает жесткость.

Приведенная выше информация указывает на то, что провести расчет требуемого показателя проводится следующим образом: E=kl²/2. В этом случае величина во многом зависит от удлинения и коэффициента жесткости.

Изменение кинетической энергии

Приведенная выше информация указывает на то, что рассматриваемое значение не имеет постоянный показатель. Среди особенностей отметим:

1. Наибольшее значение характерно максимальному удлинению витков относительно друга друга. При этом не стоит забывать о том, что есть определенное ограничение, касающееся максимального удлинения, так как слишком большая нагрузка становится причиной деформации.
2. При приближении тела к точке равновесия оно снижается. Это связано с тем, что показатель упругости существенно снижается.

Кроме этого, параметр зависит от воздействия других сил. Примером можно назвать трение, которая снижает скорость перемещения объекта.

Средняя кинетическая энергия

В большинстве случаев проводится высчитывание среднего значения. Этот показатель не учитывает то, в каких положениях сила упругости высокая и низкая. Для расчета применяется формула: F=kl/2.

В данном случае достаточно знать лишь удлинение, которое измеряется при использовании обычного инструмента. Что касается коэффициента, то он может варьировать в достаточно большом диапазоне, зависит от следующих моментов:

1. Диаметра витков. С увеличением этого показателя существенно повышается коэффициент жесткости, изделие часто используется для выполнения большой работы.
2. Толщины применяемой проволоки. Рассматриваемое изделие представлено проволокой, которая накручивается вокруг установленной оси.
3. Расстояния между отдельными витками. Как правило, они расположены относительно друг друга на определенном расстоянии, которое одинаковое. По этому признаку выделяют варианты исполнения, предназначенные для сжатия и растяжения.
4. Типа применяемого материала при изготовлении. Некоторые сплавы характеризуются достаточно высокой жесткостью, могут переносить незначительную деформацию.

Коэффициент самостоятельно рассчитать не нужно, он берется с определенных таблиц. Среднее значение часто высчитывается в случае решения математических задач, при проектировании применяются другие формулы.

Связь между внутренней энергией тела кинетической и потенциальной энергиями

Между кинетической и потенциальными понятиями есть определенная взаимосвязь. Для расчета подобной связи используется следующая формула: А=Fs=mav²₂-v²₁/2a.

Оба значения применяются в качестве полезного действия, могут варьировать в достаточно большом диапазоне, а также зависеть от различных факторов.

В заключение отметим, что проводимые расчеты позволяют выбрать наиболее подходящий вариант исполнения изделия для конкретного механизма. При исследовании проводится отображение схемы, на которой можно увидеть распространение всех сил.

Рассмотрим процесс превращения энергии при колебательном движении идеального горизонтального пружинного маятника.

Будем считать, что в системе сил трения и сил сопротивления нет. Когда эта система находится в равновесии, и никакого колебания не происходит, скорость тела равна нулю, и отсутствует деформация пружины. В этом случае энергии у данного маятника нет.

Выводя тело из положения равновесия, например, сжимая пружину на некоторую величину, ему сообщается некоторый запас потенциальной энергии: Eпkx22.

Если теперь отпустить груз, не удерживать его, то он начнет свое движение к положению равновесия, пружина начнет выпрямляться и деформация пружины будет уменьшаться. Следовательно, будет уменьшатся и ее потенциальная энергия. Скорость же тела будет увеличиваться, и по закону сохранения энергии потенциальная энергия пружины будет превращаться в кинетическую энергию движения тела:

Eкmv

.

В момент прохождения те­лом положения равновесия его по­тенциальная энергия равна нулю, а кинетическая будет максимальна.

Потом вступает в действие явление инерции. Тело, которое обладает некоторой массой, по инерции проходит точку равновесия. Скорость тела начинает уменьшаться, а деформация, удлинение пружины, увеличивается. Следовательно, кине­тическая энергия тела убывает, а потенциальная наоборот, возрастает.

В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна.

Таким образом, при колебаниях периодически проис­ходит переход потенциальной энергии в кинетическую и обрат­но. Обрати внимание!

Полная механическая энергия пружинного маятника в каждой точке его траектории постоянна и равна сум­ме его кинетической и потенци­альной энергий: Emv22kx22.

Если для вертикального пружинного маятника выбрать систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю, то все описанное выше для горизонтального маятника можно применить для данного маятника. Источники:

ОпределениеПружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид: [ddot{x}+{omega }^2_0x=0left(1right),] где ${щu}^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),] где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний. В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).].

[custom_ads_shortcode1]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы: [T=2pi sqrt{frac{m}{k}}left(4right).] Так как частота колебаний ($nu $) – величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).].

[custom_ads_shortcode2]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $). Амплитуду можно найти как:

None [tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),] где $v_0$ – скорость груза при $t=0 c$, когда координата груза равна $x_0$.

[custom_ads_shortcode3]

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис. 2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат.

Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

None [E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).] Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),] где $dot{x}=v$ – скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ – кинетическая энергия маятника. Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

[custom_ads_shortcode1]

Примеры задач с решением

Пример 1Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?

Решение. Сделаем рисунок.

По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

[E_{pmax}=E_{kmax }left(1.1right),] где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ – кинетическая энергия шарика, в момент прохождения положения равновесия. [E_{kmax }=frac{mv^2}{2}left(1.2right).] Потенциальная энергия равна:

None [frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).] Из (1.4) выразим искомую величину:

[x_0=vsqrt{frac{m}{k}}.] Вычислим начальное (максимальное) смещение груза от положения равновесия:

[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).] Ответ. $x_0=1,5$ ммПример 2Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ – постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$. В какой момент времени это произойдет?

Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:

None [E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).] В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:

[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.] Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$Читать дальше: формулы равноускоренного прямолинейного движения.

Модель иллюстрирует превращения энергии при гармонических колебаниях тела под действием силы упругости, потенциальная энергия которой пропорциональна квадрату смещения тела из положения равновесия: где A > 0 – коэффициент пропорциональности. В случае колебаний груза на пружине: где k – жесткость пружины. Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

F (t) = ma (t) = –mω2x (t).

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kxСилы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины. Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

None

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени. Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия.

Пружинный маятник — это груз массой т> прикрепленный к абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы:

где k — жесткость пружины.

Сила тяжести mg, действующая на пружинный маятник, уравновешивается силой упругости опоры (рис. 367). Если вывести шарик из положения равновесия, сместив его вдоль оси X_f то маятник начнет совершать колебания около положения О, двигаясь поступательно. Смещение шарика х в любой момент времени равно деформации пружины, а сила упругости F пружины направлена в сторону, противоположную смещению маятника.

Если начало координат совпадает с положением равновесия пружинного маятника, то, согласно закону Гука,.

где F — сила, действующая на шарик (сила упругости пружины), х — смещение маятника.

По второму закону Ньютона.

где т — масса шарика пружинного маятника, а — его ускорение. Следовательно:

или.

None где со0 — собственная циклическая (круговая) частота свободных колебаний равна Решение уравнения (3) имеет вид:

т.е. пружинный маятник совершает гармонические колебания с циклической частотой (3) и периодом

Формула (5) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука и когда масса пружины пренебрежимо мала по сравнению с массой тела (шарика). При гармонических колебаниях пружинного маятника происходит (см. п.

13. 2) превращение его потенциальной энергии.

(потенциальная энергия пружинного маятника — это энергия, запасенная в пружине) в кинетическую.

(кинетическая энергия пружинного маятника — это энергия движения), где k — жесткость пружины, х — абсолютное значение смещения маятника из положения равновесия, m — масса тела, v — его скорость.

Полная энергия пружинного маятника.

Как уже указывалось, упругая сила консервативна, поэтому превращения энергии при гармонических колебаниях пружинного маятника происходят в соответствии с законом сохранения механической энергии. В любой точке между положениями равновесия и максимального отклонения маятник обладает и кинетической, и потенциальной энергией, ноkA.2сумма этих энергий, т.е. полная энергия, равна -. Следо-2вательно, полная механическая энергия пружинного маятника пропорциональна квадрату амплитуды его колебаний.

Полная энергия пружинного маятника, совершающего незатухающие гармонические колебания, постоянна и равна максимальной кинетической (в положении равновесия) или максимальной потенциальной (в крайних точках) энергии. Тогда

откуда вытекает связь между амплитудой А колебаний и максимальной скоростью V_max пружинного маятника:

Page 2

Посмотреть оригинал

Источники:

• www.yaklass.ru
• www.webmath.ru
• files.school-collection.edu.ru
• bstudy.net