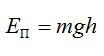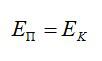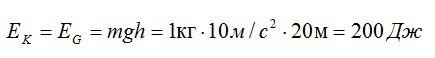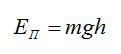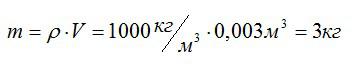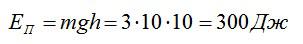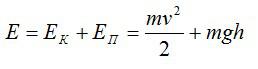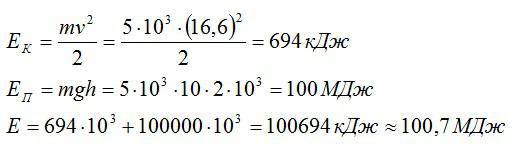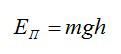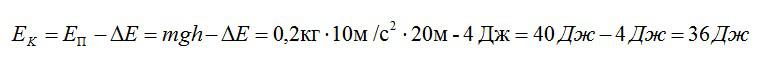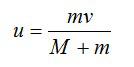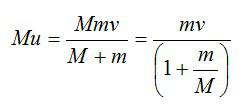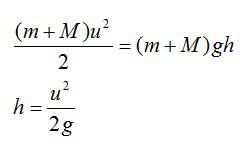А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.
А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.
Задачи на кинетическую и потенциальную энергию
Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.
Задача №1 на кинетическую энергию
Условие
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Потенциальная энергия тела над поверхностью Земли составляет:
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:
Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:
Ответ: 200 Дж.
Задача №2 на потенциальную энергию
Условие
Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?
Решение
По определению, потенциальная энергия равна в поле силы тяжести равна:
Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:
Осталось вычислить потенциальную энергию:
Ответ: 300 Дж.
При решении задач не забывайте переводить все размерности величин в систему СИ.
Задача №3 на полную механическую энергию
Условие
Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?
Решение
Полная механическая энергия состоит из кинетической и потенциальной энергий:
Вычислим:
Ответ: 100,7 МДж.
Задача №4 на кинетическую и потенциальную энергию
Условие
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Решение
Перед началом падения потенциальная энергия шарика составляет:
По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:
Ответ: 36 Дж.
Задача №5 кинетическую и потенциальную энергию
Условие
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна
Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.
Найдем импульс, переданный шарику при попадании пули:
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.
Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
Ответ: см решение выше.
Вопросы на потенциальную и кинетическую энергию
Вопрос 1. Что такое энергия? Что такое механическая энергия?
Ответ. Для энергии существует множество определений. В наиболее общем смысле:
Энергия – мера способности тела совершать работу.
Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.
Вопрос 2. Сформулируйте закон сохранения энергии
Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.
Вопрос 3. Какие силы называются консервативными?
Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.
Вопрос 4. Какую энергию называют кинетической?
Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.
Вопрос 5. Какую энергию называют потенциальной?
Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.
Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.
Кинетическая энергия твердого тела
При применении теоремы об изменении кинетической энергии системы часто приходится вычислять кинетическую энерпно движущегося твердого гела. Найдем ее выражение при важнейших видах движения тела.
Тело движется поступательно
Пели тело движется поступательно, то скорости всех его точек в каждый момент равны между собой. Следовательно. в данном случае кинетическая энергия тела
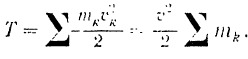
Обозначая 
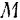
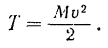
Кинетическая энергия 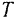
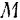
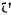
Таким образом, кинетическая энергии поступательно движущегося тела, как этого и можно было ожидать, вычисляется совершенно одинаково с кинетической энергией материальной точки.
Но формуле (208) вычисляется также и кинетическая энергия любой системы, движущейся так, что модули скоростей всех ее точек одинаковы.
Тело вращается вокруг неподвижной оси.
Модуль 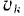
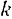
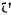
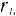
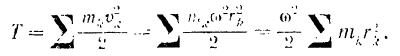
Но
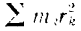
есть момент инерции 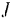
Следовательно, при вращательном движении тела
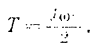
Кинетическая энергии 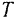
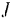
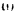
Сравнивая формулу (209) с формулой (208) можно заметить что строение их аналогично. В формуле (209) роль линейной скорости точки играет угловая скорость тела, а роль массы момент инерции тела (мера его инерции при вращательном движении.
Тело совершает плоское движение.
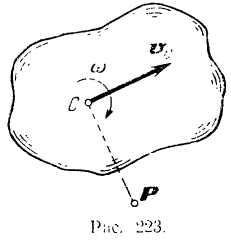
Пусть тело совершает плоское движение. Представим себе сечение тела (рис. 223) плоскостью проходящей через центр тяжести 
Зная это. нетрудно найти и положение мгновенного центра скоростей фигуры. Он лежит (см. § 63) па перпендикуляре. восстановленном из какой-либо точки фигуры к направлению скорости этой точки, на расстоянии, разном отношению скорости данной точки к угловой скорости фигуры. Следовательно, искомое расстояние
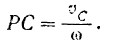
При плоском движении тола скорости его точек каждый момент распределяются так, как будто бы тело вращается в этот момент вокруг мгновенной оси (см. § 64), проходящей через соответствующий данному моменту мгновенный центр скоростей фигуры и перпендикулярной к ее плоскости.
Но кинетическая энергия тела
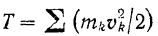
зависит только от массы каждой его точки и ее скорости, и поэтому соответствующую данному моменту кинетическую энергию тела, совершающего плоское движение, можно вычислить по формуле (209):
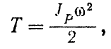
где 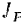
Пользование формулой (209) для нахождения кинетической энергии тела при его плоском движении затрудняется тем, что требует для каждого момента времени определения положения мгновенной оси вращения тела и вычисления соответствующего ей момента инерции тела. Преобразуем полученную формулу, воспользовавшись теоремой о моментах инерции относительно параллельных осей (§ 80). Согласно этой теореме
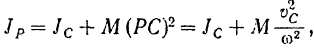
где 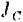
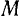
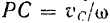
Подставив полученное выражение для момента инерции 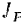
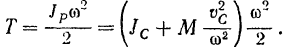
Раскрыв скобки и произведя сокращение, окончательно получим:
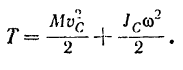
Кинетическая энергия тела при его плоском движении равна сумме тех кинетических анергий, которые имело бы данное тело при его поступательном движении со скоростью центра масс тела и при его вращательном движении вокруг оси, проходящей через центр масс тела и перпендикулярной к неподвижной плоскости, параллельно которой движется тело.
Данную формулировку нетрудно запомнить, если принять во внимание, что всякое плоское движение может быть разложено на поступательное движение со скоростью полюса и вращательное движение вокруг полюса (§61).
Только в отличие от кинематики выбор полюса здесь не произволен. При вычислении по формуле (210) кинетической энергии тела при его плоском движении за полюс надо обязательно выбирать центр масс тела. Если за полюс принять другую точку тела, то мы получим иную, чем (210), формулу для его кинетической энергии.
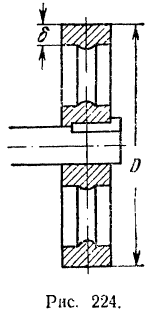
Пример задачи:
Маховое колесо (рис. 224), пес обода которого 
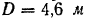
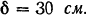
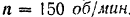
Решение:
По теореме о кинетической энергии системы
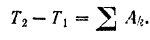
Кинетическую энергию маховика в конце рассматриваемого периода его работы определим по формуле (209) 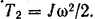
Изменение кинетической энергии маховика происходит только за счет приложенного к нему постоянного вращающего момента, работа которого согласно формуле (202) равна
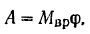
где 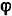
Таким образом, уравнение кинетической энергии системы принимает вид
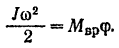
Отсюда искомый момент сил равен
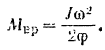
Момент инерции 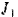
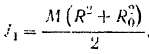
Наружный радиус обода
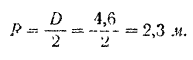
Внутренний радиус обода
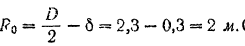
Следовательно, момент инерции обода
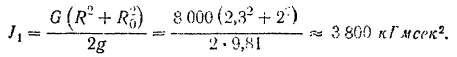
Момент инерции спиц и втулки
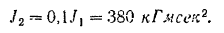
Момент инерции всего маховика
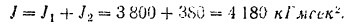
Угловая скорость маховика
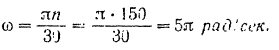
Угол, на который повернется маховик, сделав
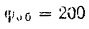
оборотов, равен
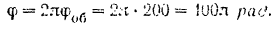
Подставляя числовые данные, определяем весомый момент сил
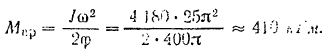
Пример задачи:
На шкив (рис. 225) радиуса 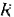
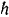
Решение:
Так как система сначала находилась в покое, то се начальная кинетическая энергия 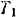
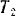
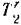
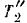
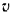
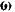
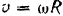
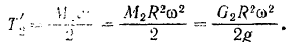
Кинетическая энергия шкива равна
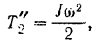
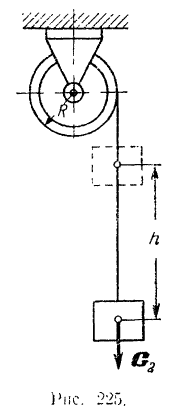
где 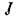
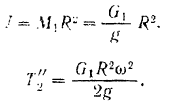
А кинетическая энергия всей системы
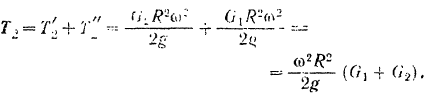
Так как кинетической энергии системы происходит только за счет работы силы тяжести опускающегося на высоту 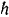
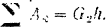
Таким образом, уравнение кинетической энергии системы приобретает вид
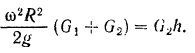
Отсюда искомая угловая скорость шкива
Пример задачи:
Танк (рис. 226) приводится в движение двигателем. который вращает четыре колеса (по два с каждой стороны). Колеса своими выступами захватывают гусеницы. Определить скорость танка через 10 сек после начала его движения, если средняя полезная мощность двигателя танка 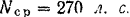
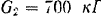
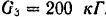
Решение:
Рассматриваемая система состоит; 1) из поступательно движущегося корпуса танка, 2) двух гусениц, каждая из которых движется поступательно вместе с танком и одновременно с той же скоростью совершает движение относительно корпуса танка, и 3) четырех колес, вращающихся вокруг своих осей и вместе с ними перемещающихся поступательно, т. е. совершающих плоское движение.
Кинетическая энергия корпуса танка равна
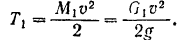
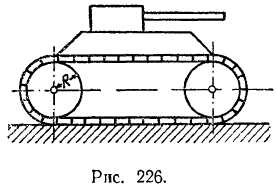
Кинетическая энергия гусениц
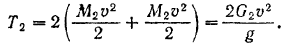
Скорость точек оси колеса равна поступательной скорости танка. Следовательно, угловая скорость колеса 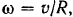
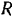
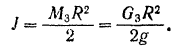
Таким образом, кинетическая энергия колес:
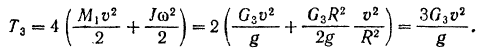
Кинетическая энергия всего танка
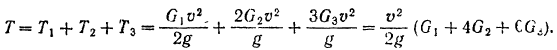
Так как в начале движения танка его кинетическая энергия равна нулю, то уравнение (207) кинетической энергии системы принимает вид
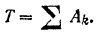
Следовательно, полезная работа двигателя, приводящего в движение танк,
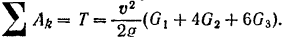
Средняя полезная мощность двигателя (в лошадиных силах)
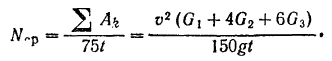
Отсюда скорость танка через 10 сек после начала его движения
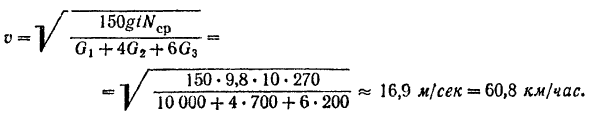
Пример задачи:
Шестерня I (рис. 227), ось которой проходит через точку 

Радиус шестерни I (сателлита) — 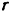
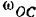
Решение:
Рассматривая кривошип и шестерню I как одну систему, применим к ней теорему об изменении кинетической энергии системы:
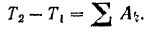
Так как вначале система была неподвижна, то 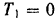
Находим кинетическую энергию 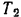
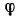
Кривошип совершает вращательное движение вокруг неподвижной оси 
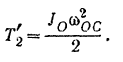
Момент инерции однородного стержня относительно оси, проходящей через его конец (задача 71).
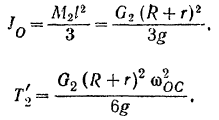
Шестерня I совершает плоское движение. По формуле (210) ее кинетическая энергия
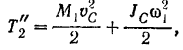
где 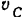
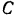
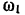
Точка 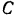
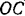
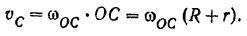
Мгновенный центр 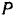
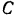
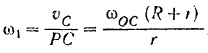
Момент инерции шестерни I (однородного сплошною цилиндр) относительно ее центральной оси:
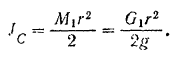
Подставляя найденные значения угловой скорости, скорости центра масс и момента инерции в выражение для кинетической энергии шестерни I, находим:
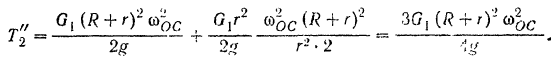
Кинетическая энергия осой системы
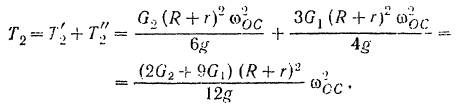
Вычисляем теперь сумму 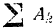
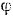
Механизм расположен в горизонтальной плоскости. Следовательно, работа сил тяжести, приложенных ко всем частям системы, равна нулю. Трением в осях мы пренебрегаем. Таким образом, изменение кинетической энергии нашей системы происходит только за счет работы постоянного вращающего момента 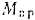
Таким образом, в соответствии с формулой (202)
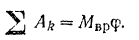
Подставляя найденные значения
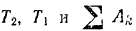
уравнение кинетической энергии системы, получаем:
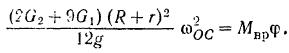
Отсюда искомая угловая скорость кривошипа
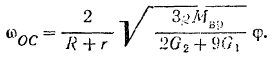
Для того чтобы определить угловое ускорение кривошипа, продифференцируем по времени обе часта уравнения кинетической энергии:
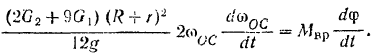
Принимая во внимание, что
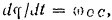
и сокрушая на 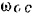
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
Кинетическая энергия является одним из важнейших понятий современной механики, к которому наука пришла в результате долгого ее развития. Правда, в настоящее время еще не до конца понята сущность кинетической энергии. Поэтому в учебниках ее часто характеризуют с помощью формулы:
, (1)
где m – масса тела, V— скорость его движения, утверждая, что именно эта формула и определяет сущность кинетической энергии. В других учебниках кинетическую энергию связывают с работой, которую может совершить движущееся тело. Например, в книге [31, с.137] дается такое определение: “Этот запас работы, которую тело может совершить потому, что оно обладает скоростью, представляет собой кинетическую энергию тела”. Иногда дают более широкое определение кинетической энергии, как меры механического движения.
Очевидно, что энергия, как и масса, и движение есть свойство движущейся материи. Но каковы особенности этого свойства, как они проявляются, чем характеризуются? Вот в этом и предстоит разобраться.
Для выявления сущности и свойств кинетической энергии необходимо рассмотреть взаимодействие материальных объектов. При их взаимодействии будет происходить изменение в их механическом состоянии: они или начнут двигаться, или изменят характер своего движения, или только деформируются. Кроме этого, при взаимодействии будут изменяться и такие свойства материальных объектов, как количество движения (или импульс) mV и потенциальная энергия деформации, так как эти свойства тесно связаны друг с другом и являются конкретными характеристиками движения и взаимодействия материальных объектов. Сущность этих свойств материальных объектов мы тоже рассмотрим.
Представим себе, что в какой-то произвольный момент времени на тело будет оказываться воздействие со стороны других тел. Пусть это воздействие будет осуществляться непрерывно, то есть на тело в каждый момент времени будет оказываться какое-то мгновенное воздействие, которое назовем фактором воздействия (см. рис.1). Это мгновенное воздействие должно как-то влиять на состояние тела или на характер его движения. Из опыта известно, что при внешнем воздействии скорость движения свободного, то есть незакрепленного тела, изменяется. Однако, вполне очевидно, что мгновенное изменение скорости при мгновенном воздействии не может иметь какую-то конечную величину, то есть величина скорости не может изменяться вообще. Тогда что же будет изменяться? Можно сказать, что при внешнем мгновенном воздействии в движении тела появится какая-то особенность (назовем ее потенцией), которая в дальнейшем и приведет к изменению скорости тела при его перемещении в пространстве. Эта “потенция” должна, конечно, каким-то образом характеризовать изменение скорости тела, причем в данной точке пространства, соответствующей мгновенному воздействию. Такой характеристикой изменения скорости при отсутствии мгновенного пространственного перемещения может быть только мгновенное изменение скорости во времени, а именно отношение
, представляющее собой производную скорости по времени, то есть ускорение. Такое отношение, а не
надо брать еще и потому, что само понятие скорости является отношением перемещения ко времени, а это значит, что само перемещение и его скорость мы рассматриваем как функцию времени.
Очевидно, что при одной и той же величине мгновенного воздействия, мгновенное изменение скорости во времени будет зависеть от массы тела, то есть чем больше будет масса тела, тем меньше будет
, и наоборот. В соответствии со сказанным можно принять в качестве гипотезы следующее соотношение:
, (2)
где m – масса тела. Данное соотношение вполне очевидно, так как с увеличением массы тела изменение его скорости будет меньше. Запись выражения (2) должна быть сделана в векторной форме, так как мгновенное воздействие и, следовательно, изменение скорости должно происходить в направлении, совпадающим с направлением мгновенного воздействия
.
Следует обратить внимание на следующие обстоятельства в наших рассуждениях. Мы рассматриваем движение конкретного материального объекта, имеющего определенные размеры и занимающего определенный объем в пространстве. Когда мы говорим о мгновенной скорости тела, то полагаем, что все его точки имеют одинаковое изменение скорости в данный момент времени. Но так будет, очевидно, не всегда. Это будет зависеть от характера мгновенного воздействия. Так, если мгновенное воздействие будет одним и тем же для всех точек тела, то условие (2) будет справедливо для всего тела в целом. Такое, например, возможно при гравитационном воздействии. В случае же “местного” воздействия на тело, когда воздействие будет последовательно передаваться от одной точки тела к другой его точке, мгновенное изменение скорости точек будет происходить с некоторым запозданием за счет конечной скорости передачи воздействия. Тогда соотношение (2) не будет точно выполняться для всего тела в целом. Его можно считать в этом случае с какой-то степенью точности усредненным выражением, отнесенным к какой-либо одной точке тела, например, к центру масс или к одной из крайних по движению точек тела. Влияние этого обстоятельства на характер движения тела будет рассмотрено нами во второй главе. При таком внешнем воздействии на тело оно обязательно будет деформироваться.
Если тело закреплено и не сможет двигаться под действием внешнего воздействия, соотношение (2) также не будет выполняться, поскольку никакого изменения скорости в этом случае быть не может. Тело же просто будет деформироваться. Упоминаемая нами “потенция” воздействия будет поддерживать тело в деформированном состоянии. Значит, гипотеза в форме выражения (2) здесь вообще не годится.
Выражение (2) для движущегося тела можно представить в общепринятом виде:
, (3)
откуда следует, что вектор внешнего воздействия представляет собой силу воздействия
. Следовательно, сила
является характеристикой мгновенного воздействия при взаимодействии материальных объектов, тогда как по существующим воззрениям сила есть мера механического взаимодействия тел. Как следует из наших рассуждений, такое определение силы неверно, поэтому мерой взаимодействия должна быть другая характеристика движущейся материи. Следует также отметить, что данное нами определение силы является качественным и не определяет её физического смысла.
Так как выражение (3) представляет собой по форме второй закон Ньютона, то можно сказать, что этот закон является гипотезой в ранге аксиомы, подтвержденной экспериментально с определенной степенью точности. С помощью этого закона может быть найдена величина силы F, но он не может служить определением ее физической сути.
Продолжим наши рассуждения. Поскольку движение непрерывно и, как было показано выше, состоит из бесконечной суммы мгновенных положений, все мгновенные взаимодействия можно просуммировать. Вполне очевидно, что такое суммирование может быть произведено только по реальному перемещению тела в пространстве S, так как движения тел во времени не существует (движение во времени является квазидвижением). Тогда при элементарном перемещении тела в направлении, отличном от направления действия силы
(см. рис.2), из выражения (3) получаем следующее выражение для суммарного воздействия:
, (4)
представляющего собой скалярные произведения двух векторов и
в левой части и двух векторов
и
— в правой. В соответствии с этим выражение (4) может быть представлено в следующем виде:
, (5)
где ,
— угол между направлением действия силы
и направлением перемещения тела
. Этот угол в общем случае взаимодействия будет переменным.
Так как произведение представляет собой проекцию силы на направление движения dS, выражение (5) можно записать в виде:
(6)
Чтобы найти суммарное воздействие силы на конечном перемещении S, возьмем интеграл от выражения (6) при изменении параметров интегрирования в соответствующих пределах:

откуда получим:

Интеграл в выражении (8) принято называть работой A силы на перемещении S. На основании этого выражения можно сделать вывод, что мерой взаимодействия материальных объектов при их движении в пространстве является изменение кинетической энергии. Следовательно, работа представляет собой приобретенную или затраченную телом кинетическую энергию. В этом заключается физическая сущность работы. При увеличении энергии тела работа будет положительной, при уменьшении – отрицательной.
Выражение (8), представленное в виде:
, (9)
называется теоремой об изменении кинетической энергии.
Выражение (4) можно записать в виде проекций на оси координат:


Интегрируя эти выражения, получим:


Суммарная работа силы F и полное изменение кинетической энергии тела определяется выражением:
, (14)
что соответствует выражению (8).
Для проверки полученного результата решим эту задачу аналитическим методом при проектировании силы F на оси координат x и y и на направление движения тела S (на касательную к траектории его движения).
В первом случае получаем:
; (15)
(16)
Величину силы F и направление ее действия , то есть угол , считаем постоянными. Решаем эти уравнения с учетом начальных условий:
(17)
(18)
в результате получаем:
(19)
(20)
(21)
(22)



где .
Полная кинетическая энергия тела будет равна:

Определим величину результирующей скорости, используя выражения (19) и (20):

где .
В соответствии с этим выражением формулу (26) можно представить в виде:
, (28)
так как выражение в последней скобке этой формулы соответствует квадрату скорости из выражения (27). Этот квадрат результирующей скорости можно представить как квадрат модуля при сложении двух векторов и
(рис.3), где второй вектор направлен по линии действия силы F. Из выражения (28) следует, что
.
Теперь найдем изменение энергии тела в соответствии с выражением (8), то есть используя проекцию силы F на направление движения тела:

где ,
. Преобразуем выражение для
:
,
в которое подставим значения и
, в соответствии с выражениями:
(30)

тогда получим:

Подставим это значение в выражение (29) и возьмем интеграл:

Это выражение точно соответствует полному изменению энергии тела (сравните с выражением (25)).
Таким образом, полную кинетическую энергию тела можно представить в виде:
, (34)
что представляет собой сложение скалярных величин:

где добавочные скорости и
могут быть найдены с помощью выражений (23) и (24):
откуда следует:
(36)
(37)
Однако, в соответствии с выражениями (23) и (24), можно утверждать, что сложение кинетических энергий будет происходить не по правилам векторной алгебры. Дело в том, что по правилам векторной алгебры скалярные величины квадратов векторов могут только складываться, какое бы направление эти вектора не имели. Изменение же кинетической энергии и
, являясь функцией квадратов векторов
и
, могут иметь как положительное, так и отрицательное значение в зависимости от величины угла
. Поэтому при определенных значениях угла
кинетические энергии будут не складываться, а вычитаться, то есть кинетические энергии будет вести себя как проекции каких-то векторов на оси координат. На рис.4 показаны проекции кинетических энергий
,
,
и
на осях координат и предполагаемые вектора
и
, соответствующие этим проекциям. Результирующий вектор
определяется обычным сложением векторов
и
. Только все эти векторы не могут быть использованы для определения скоростей движения тела, так как их модули определяются не суммой проекций энергий. Поэтому эти векторы следует рассматривать как псевдовекторы, то есть не как настоящие векторы. Но тогда какой смысл вводить эти ненастоящие векторы? Смысл здесь заключается только в одном: показать, что скалярные величины могут складываться с учетом их знака, определяемого положением псевдовекторов. В векторной алгебре это не предусматривается, хотя ничего необычного в введении понятия псевдовектора кинетической энергии нет, так как это соответствует реальным фактам. Математики, например, утверждают, что смысл скалярных и векторных произведений векторов определяется той пользой, которую они приносят в физических приложениях [35, с.123]. В предлагаемом нами способе такой смысл несомненно есть, так как поведение тела будет зависеть от направления подведенных к нему энергий. Если тело будет находиться в равновесии, то вся подведенная энергия пойдет на повышение его внутренней энергии за счет деформации.
Если тело будет двигаться, то часть энергии может затрачиваться на движение, а часть на его деформацию, то есть часть подведенной энергии будет вызывать движение, а часть – тормозить его. Поскольку их действие будет противоположным, то и при сложении подведенных к телу энергий надо учитывать их направление, то есть знак. Поэтому при сложении энергий надо учитывать направление их составляющих по осям координат.
Так как кинетическая энергия тела зависит от квадрата скорости, который можно представить как скалярное произведение двух одинаковых векторов, то это произведение по правилам векторной алгебры можно представить в виде:
, (38)
откуда следует правило разложения кинетической энергии по взаимно перпендикулярным осям координат:
(39)
Связь между полной энергией и ее составляющими по осям координат, может быть установлена с помощью проекций скоростей:

где ,
и
— направляющие косинусы для скорости тела. Тогда получим:

Если тело под действием подведенных энергий будет находиться в равновесии, то выражать энергию через скорость нельзя. Поэтому в этом случае следует использовать другой способ выражения энергии -–через работу сил, то есть в виде:
, (42)
где работа на элементарном перемещении
является скалярным произведением двух векторов: силы
и перемещения
(берем небольшое перемещение, поскольку оно является деформацией тела). Можно сказать, что здесь знак работы или изменения энергии уже заложен в косинусе угла между направлением силы
и направлением перемещения
. Однако, это утверждение будет справедливо только в том случае, когда
представляет собой реальное перемещение тела под действием всех приложенных к нему сил. Тогда для одних сил это перемещение будет совпадать с направлением их действия и их работа будет положительна, для других же сил все будет наоборот, то есть в этом случае направление силы по отношению к перемещению и определяет знак ее работы. Если же тело будет находиться в равновесии, то каждая сила вызовет деформацию тела в направлении своего действия и работы всех сил, в связи с этим, будут положительными. Очевидно, знак работы для сил, под действием которых тело находится в равновесии, должен определяться направлением взаимного действия сил. Это важное обстоятельство не учитывается в настоящее время при доказательстве и использовании принципа возможных перемещений, когда для определения элементарных работ всех сил задается элементарное перемещение всему телу, принимаемому за единое жесткое целое. Тогда получается, что вопреки утверждению о равновесии тела, тело все же движется. Чтобы выйти из этой неприятной ситуации и дать более или менее правдоподобное объяснение сущности принципа возможных перемещений, перемещение тела объявляется не условным, как это и есть на самом деле, а возможным или виртуальным, что звучит, конечно, значительно солиднее, но ясности нисколько не прибавляет. Получается, что это перемещение как бы есть, но с другой стороны его, вроде, как бы и нет. В этом заключается одна из причин непонимания физической сущности принципа возможных перемещений. К счастью, это обстоятельство не препятствует использованию самого принципа, так как деформации тела под действием приложенных к нему сил в случае его равновесия взаимосвязаны, что и будет показано ниже.
Таким образом, и в случае скалярного произведения двух различных векторов должно учитываться направление этого скаляра по отношению к скалярным произведениям других векторов.
Рассмотренные нами вопросы не обсуждаются в учебниках по механике, хотя о возможности разложения кинетической энергии по осям координат говорил еще Макс Планк. Процитируем его рассуждения, которые представят для нас несомненный интерес [36, с.145-147]: “Простейшей материальной системой является материальная точка, внутреннее свойство которой определяется только ее неизменной массой. Ее энергией является живая сила:
плюс произвольная постоянная, которую мы положим равной нулю, как это делается обычно.
Живая сила, согласно принципу сохранения энергии, остается постоянной до тех пор, пока на точку не производится извне никаких воздействий. Но если производится внешнее действие, то есть если на рассматриваемую материальную точку действуют силы, исходящие от других материальных точек, то эти силы за известный промежуток времени вызывают изменение энергии материальной точки, величина которого определяется работой этих действий, то есть работой, которую за данное время совершают силы над рассматриваемой точкой; и это справедливо всегда, из какого бы источника ни происходили названные силы.
Применяя это положение к элементу времени , получим выражение для суммы соответствующей работы всех сил, действующих на точку, в такой форме:
,
где X, Y, Z — суть компоненты результирующей силы, взятые по направлению трех координатных осей. На основании приведенного ранее положения получаем, что прирост энергии за бесконечно малое время , то есть дифференциал выражения живой силы, равен указанной здесь величине работы…
Примем во внимание, что выражение энергии рассматриваемой точки представляется в виде суммы трех симметрично построенных членов, каждый из которых относится к определенной оси координат и зависит только от соответствующей переменной. Полная энергия составляется, следовательно, из трех независимых друг от друга видов энергий. Но совершенно то же самое свойство мы замечаем и в выражении работы действующих извне сил. Эта величина также распадается на три слагаемых, каждая из которых соответствует определенной оси координат и имеет значение, независимое от двух других; таким образом, каждое отдельное внешнее действие соответствует определенному отдельному виду энергии. Естественно предположить, что не только изменение полной энергии измеряется полной работой внешних сил, но что каждый из названных видов энергии меняется только в зависимости от непосредственно ему соответствующего действия и совершенно не зависит от двух других. Если мы будем считать эту мысль правильной, то приведенное выше уравнение распадается на три отдельных уравнения, каждое из которых относится к определенной оси координат:
а произведя дифференцирование, получаем уравнения движения Ньютона:
которых достаточно для характеристики всего движения.
Само собой понятно, что этот вывод ни в какой степени не может претендовать на доказательство двух первых ньютоновских аксиом, так как указанный закон суперпозиции энергий не может быть применен a priori. Напротив, его значение…основано главным образом на его эвристической ценности…то, что действия по трем осям координат происходят независимо друг от друга, также является опытным законом…”.
Мы привели такую длинную цитату потому, что в ней заложены идеи, которые используются и развиваются автором данной книги.
Вернемся снова к рассмотрению нашей задачи о движении тела в результате внешнего воздействия. Из выражения (6) непосредственно вытекает следующее очень важное соотношение между силой и кинетической энергией:

то есть сила взаимодействия между материальными объектами в выбранном направлении представляет собой производную от кинетической энергии по перемещению S в данном направлении.
Однако, поскольку в данном случае кинетическая энергия не представляет собой какую-то субстанцию, непрерывно распределенную в пространстве, а является физическим свойством движущегося тела, не выходящим за его пределы, такое определение силы может быть не совсем понятно. Большую ясность о физической сущности силы можно получить, если представить производную в другом виде:
, (44)
где — изменение кинетической энергии тела при его перемещении на величину
.
Исходя из этого выражения, силу можно определить как количество изменения энергии при взаимодействии тел, приходящееся на единицу перемещения S. В пределе же при стремлении к нулю значение силы будет стремиться к производной, то есть к мгновенному значению отношения
к
в выбранном положении, что, таким образом, и представляет собой скорость изменения кинетической энергии тела при его перемещении в пространстве. Такая формулировка может служить определением силы, раскрывающим её физическую сущность
Для пространственной системы координат на основании выражения (43) можно найти три проекции силы:



Таким образом, в результате суммирования мгновенных воздействий на материальный объект по его пространственному перемещению мы получили ряд интересных следствий, получили представление о физической сущности силы и кинетической энергии. Еще раз отметим, что кинетическая энергия – это такое физическое свойство движущихся материальных объектов, которым они обмениваются при взаимодействии, приобретая или теряя его, и которое может служить определением работы. Можно также сказать, что энергия, а не сила, является мерой механического взаимодействия тел. Сила же характеризует скорость изменения энергии тел при их перемещении в пространстве или, что одно и то же, мгновенное воздействие на тело в данном положении при взаимодействии материальных объектов.
Однако, можно произвести суммирование мгновенных воздействий и по времени, то есть при квазидвижении тел. Тогда на основании выражения (3) получим:
, (48)
где левая и правая части представляют собой вектора. Проинтегрировав выражение (48), найдем:

где произведение называется количеством движения или импульсом тела, а интеграл от силы по времени – импульсом силы.
Здесь следует остановиться на возможности другого толкования сущности силы в соответствии с выражением (3), которое можно представить в виде:
(50)
В такой форме записи силу можно определить как скорость изменения количества движения при движении тела во времени в выбранный момент времени. Отсюда же следует и широко используемое определение силы как произведение массы тела на его ускорение. Нами было показано, что сила является результатом изменения энергии тела при его взаимодействии с другими телами, а энергия – свойство движущихся тел, которым движущиеся тела обмениваются при взаимодействии. Но что такое количество движения, какова его физическая сущность? Количества движения можно определить как сумму мгновенных воздействий во времени. Но такое определение не раскрывает физической сущности этого понятия.
Для раскрытия физической сущности количества движения установим связь между этим понятием и кинетической энергией тела в виде:

Отсюда следует, что количество движения mV представляет собой производную от кинетической энергии тела по скорости его движения. Но такое определение тоже малосодержательно. Тогда mV можно представить как отношение конечных величин , смысл которого заключается в количестве изменения энергии, приходящемся на единицу изменения скорости при взаимодействии материальных объектов, причем чем больше будет
или меньше
, тем больше будет величина этого отношения и, следовательно, больше величина mV.
Увеличение потребляемой (или отдаваемой) энергии при одном и том же изменении скорости или, наоборот, уменьшение изменения скорости при одном и том же изменении энергии при взаимодействии материальных объектов характеризует инертность тела. Почему именно это отношение следует считать инертностью тела, а не его инерцией? Во-первых, потому, что понятие инерции связано с первым законом Ньютона и имеет уже определившийся смысл. Во-вторых, большее потребление энергии прямо связано с противодействием движению, со свойством тела оказывать сопротивление изменению его движения, то есть с тем, что можно назвать инертностью тела. Поэтому есть все основания утверждать, что векторная величина является мерой инертности тела при его взаимодействии с другими материальными объектами. Тогда с полным правом можно будет записать:
(52)
Для иллюстрации сказанного рассмотрим движение тела под действием постоянной силы F при двух различных значениях начальной скорости . Пусть в первом случае начальная скорость будет равна нулю. Скорости движения тела и его перемещения в обоих случаях будут:
; (53)
(54)
Изменения кинетической энергии тела для обоих случаев будут соответственно равны:
; (55)

Таким образом, при одной и той же действующей силе, при одном и том же ускорении затраченная работа будет различной, так как при одном и том же времени движения. Следовательно, инертность тела во втором случае будет больше, так как будет поглощаться больше энергии. Для неподвижного тела его инертность вообще равна нулю. Отсюда также следует, что масса тела не может являться мерой его инертности, как принято сейчас считать.
Сила, определяемая через инертность тела в соответствии с выражением (50), будет характеризовать скорость изменения его инертности с течением времени (при движении тела во времени).
Таким образом, мы имеем два определения силы – через энергию и количество движения или инертность. Какое же из них важнее, какое является более общим? При решении этого вопроса следует иметь в виду, что есть силы, которые выражаются через потенциальную энергию, такие, например, как упругие силы и силы тяготения. Есть также электромагнитные силы, ядерные и другие, определяемые не по законам механики. К этим силам мы потом вернемся. Что же касается потенциальной энергии, то будет показано, что она является результатом движения материи на микроуровне, то есть результатом движения микрочастиц. Следовательно, в области механики существует два основных определения силы. Выше было показано, что реальное движение тел может происходить только в пространстве, но не во времени. Это во-первых. А во-вторых, дальше будет показано, что второй закон Ньютона не всегда может быть использован для определения силы, как, например, при движении жидкостей и газов, откуда следует, что второй способ определения силы является частным случаем выражения силы через кинетическую энергию. Второй закон Ньютона не может быть также использован при внешнем воздействии на закрепленные тела, когда они могут только деформироваться, но не двигаться. Однако, при этом их внутренняя энергия будет увеличиваться в соответствии с величиной деформации. Эта внутренняя энергия называется потенциальной энергией.
Из сказанного следует, что при взаимодействии материальных объектов изменение их состояния может быть охарактеризовано в более широком плане, охватывающем все виды взаимодействий, через изменение кинетической энергии, которое имеет место как для движущихся, так и неподвижных тел, то есть мы сразу могли бы написать выражение для такого взаимодействия в виде формулы (43). Из этого выражения можно как частный случай получить зависимость (3):

Если же внешнее воздействие связано с изменением потенциальной энергии тела, то оно может быть представлено в известном виде:

где П — потенциальная энергия деформации, k — коэффициент жесткости, dl — величина деформации.
Таким образом, вполне очевидно, что изменение состояния при взаимодействии следует характеризовать изменением энергии тел в пространстве при этом взаимодействии. Во времена Ньютона еще не было четкого понятия энергии и четкого понятия ее сущности. О кинетической энергии Лейбниц говорил как о живой силе (такая формулировка еще встречается в старых учебниках и в наши дни), о потенциальной – как о мертвой силе. Поэтому Ньютон и использовал понятие количества движения для определения силы. К счастью, понятия кинетической энергии и количества движения оказались взаимосвязанными для движущихся тел.
В заключение этого параграфа интересно рассмотреть еще две возможности представления фактора воздействия . Так, изменение скорости движущегося тела можно связать с его перемещением в пространстве, то есть представить фактор воздействия в виде:
(59)
Выражение (59) представим в виде:
(60)
Так как произведение mV характеризует импульс силы , то в соответствии с выражением (60) произведение
будет являться импульсом силы. Отсюда следуют соотношения:
(61)
и
(62)
Из выражения (62) вытекает физический смысл фактора воздействия при принятом нами условии, для чего следует найти его размерность:
Получается, что в этом случае фактор воздействия представляет собой скорость изменения массы во времени. Но это отношение можно также трактовать и как скорость подвода массы, воздействующей на тело, со стороны других тел, ведь, если разобраться, то взаимодействие происходит между реальными материальными объектами, характеризуемые количеством материи в них, то есть количеством массы. В главе VI такая физическая сущность массы будет подробно доказана. В этом случае действующая на тело сила может быть найдена из выражения (62):
(63)
И, наконец, фактор воздействия можно выразить через изменение кинетической энергии во времени:
, (64)
откуда следует, что физической сущностью фактора в данном случае является подводимое к телу количество энергии в единицу времени, то есть мощность.
Как видно, из четырех рассмотренных вариантов представления физической сущности фактора воздействия наиболее полным и содержательным является его выражение через изменение кинетической энергии по пространственной координате.
Кинетическая энергия вращения объекта равна энергии, выделяемой для выполнения работы по приложению крутящего момента.
Кинетическая энергия вращения зависит от массы и плотности, конфигурации и оси вращения точечной массы. Кинетическая энергия вращения точечной массы есть произведение массы на квадрат радиуса массы.
Обладает ли точечная масса вращательной кинетической энергией?
Точка массы вращается вокруг своей оси вращения и имеет некоторую массу и, следовательно, скорость.
Точечная масса, вращающаяся вокруг своей оси, будет непрерывно вращаться с некоторой энергией, называемой вращательная кинетическая энергия.
Вращательная кинетическая энергия точечной массы зависит от работы, необходимой для совершения движения. крутящий момент на точечной массе и угловая скорость приобретается точечной массой.
Связь между массой и вращательной кинетической энергией
Кинетическая энергия вращения точечной массы — это кинетическая энергия точечной массы относительно центра масс и определяется как
КЕ = 1/2 ω2
Где I — момент инерции точечной массы
ω — угловая скорость точечной массы
Момент инерции – это суммарная масса всех частиц, составляющих объект, и стремление массы сопротивляться угловой скорости тела. Здесь нас интересует точечная масса, а момент инерции точечной массы равен
я = мистер2
Где m — масса
И r — радиус точечной массы
Следовательно, соотношение между массой и кинетической энергией вращения имеет вид
КЭ = 1/2 мр2 ω2
Каково соотношение кинетической энергии вращения и центра масс?
Скорость вещества зависит от кинетической энергия вещества в движении.
Отношение кинетической энергии вращения и центра масс напрямую связано с отношением всей массы вокруг центра в материи к центру масс.
Кинетическая энергия вращения представляет собой полную кинетическую энергию всех масс, составляющих материю, вокруг центра масс и определяется как KE = 1/2 ω2 а кинетическая энергия центра масс представляет собой кинетическую энергию массы в центре и определяется как KE = 1/2 mv.2 .
Следовательно, отношение кинетической энергии вращения и центра масс равно
KEкрасный/КЭcm = 1/2 ω2/ 1/2 мВ2
KEкрасный/КЭcm = мистер2/мв2
Угловая скорость есть отношение скорости частицы к расстоянию от центра масс, поэтому скорость связана с угловой скоростью частицы соотношением v= ωr .
Подставляя это в приведенное выше соотношение, мы имеем,
KEкрасный/КЭcm = мистер2/мв2 = М/м
Полная кинетическая энергия представляет собой сумму кинетической энергии центра масс и кинетической энергии вращения. Отношение кинетической энергии вращения и центра масс прямо пропорционально соответствующей массе, связанной с конкретным движением.
Как рассчитать вращательную кинетическую энергию Земли?
Мы можем рассчитать кинетическая энергия вращения Земли по формуле KE = 1/2 ω2 .
Рассчитав момент инерции Земли и угловое ускорение Земли, мы можем найти значение кинетической энергии вращения Земли.
Какова кинетическая энергия вращения Земли вокруг своей оси?
Кинетическая энергия вращения Земли зависит от ее оси вращения и массы Земли.
Кинетическая энергия вращения Земли равна половине квадрата угловой скорости Земли и ее момента инерции.
Поскольку Земля имеет почти компактную сферическую форму, момент инерции Земли относительно ее оси равен
I = 2/5 МР2
Я = 2/5 * 6 * 1024 * 6.4 * (106)2
Я = 98.3 * 1036 кгм2
Мы можем рассчитать угловую скорость Земли, которая представляет собой угол, прослеживаемый Землей при совершении одного оборота за определенный интервал времени. Следовательно, угловая скорость Земли равна
ω = 2πрад/24 часа
ω = 2πрад/24 * 60 * 60 = 7.3 * 10-5 рад / с
Теперь кинетическая энергия вращения Земли равна
KEкрасный = 1/2 ω2
Подставляя все вышеперечисленные значения, которые мы рассчитали в это уравнение, мы имеем
KEкрасный = 1/2 * 98.3 * 1036 кгм2 * (7.3 * 10-5 рад / с)2
KEкрасный = 2.6 * 1029 Дж
Кинетическая энергия вращения Земли вокруг своей оси равна
2.6 * 1029 Джоули.
Как найти кинетическую энергию вращения по крутящему моменту?
Предмет вращается, когда эквивалентная величина крутящего момента применяется к краям объекта.
Следовательно, кинетическая энергия вращения тела равна работе, совершаемой при приложении крутящего момента.
Энергия, необходимая для совершения работы по приданию крутящего момента, будет преобразована в кинетическую энергию вращения тела, т. е.
W𝜏 = ∫W𝜏 = КЭкрасный .
Совершаемая работа равна крутящему моменту, действующему на тело,
W𝜏 = ∫W𝜏 dθ
Крутящий момент, приложенный к телу, равен произведению силы и смещения объекта под действием этой внешней силы. Предположим, что «r» — это смещение объекта, тогда
𝜏 = F * г
Наблюдения и советы этой статьи мы подготовили на основании опыта команды тангенциальное ускорение объекта за счет крутящего момента определяется как изменение скорости во времени.
at = дв/дт
Мы знаем, что угловая скорость связана со скоростью как
v = ωr
Следовательно,
at = dω/dt
at = гα
где α это угловое ускорение.
Мы также знаем, что F= mat
at = ф/м
rα = Ф/м
поэтому F = αmr
Теперь мы можем записать уравнение крутящего момента в виде 𝜏 =α mr2
Момент инерции равен произведению полной массы на квадрат расстояния от центра масс. То есть,
л=мистер2
Следовательно,
𝜏 = яα
Как рассчитать кинетическую энергию вращающегося тела через угловой момент?
Угловой момент объекта — это угловая скорость объекта, который вращается вокруг своей оси вращения.
По определению угловой момент есть произведение момента инерции и угловой скорости объекта, определяемое соотношением L=Iω .
Мы знаем, что кинетическая энергия вращения E равна
Е = 1/2 Iω2
Момент инерции по угловому моменту становится
I = L/ω
Используя это в приведенном выше уравнении,
E = 1/2 Lω/ω2
Е = 1/2 Lω
Следовательно, у нас есть два разных уравнения для расчета кинетической энергии вращения с точки зрения угловой момент.
Часто задаваемые вопросы
Какова скорость шарика, катящегося с горки на высоте 8 м от земли?
Объект в высота над землей имеет гравитационный потенциал энергия равна мгч.
Эта гравитационная потенциальная энергия преобразуется в кинетическую энергию поступательного движения и кинетическую энергию вращения, поскольку шар имеет круглую форму.
ПЭ = КЭтранс- + КЭкрасный
мгх = 1/2 мв2 + 1/2ω2
Для сферического объекта I = 2/5 мр2
И ω=v/r
Следовательно,
мгх = 1/2 мв2 + 1/2 * 2/5 * (в2/r2)
Удалив букву «m» и переставив полученное уравнение
гх = в2/2 + v2/5
гх = в2 (1/2 + 1/5) = 7/10 В2
v2 = 10/7 гх
Отсюда скорость тела
v= √ 10/7 гх
= √ 10/7 * 9.8 * 8
= √ 112 = 10.6 м/с
Скорость мяча 10.6 м/с.
Чему равна энергия вращения кольца, вращающегося вокруг постоянной оси, идущей из его центра, если масса кольца 556 г, радиус 12 см и угловая скорость 1.8 рад/с?
Данный: м=556 грамм=0.556 кг
г=12 см=0.12 м
ω = 1.8 рад / с
Плотность вещества в кольце – это полная масса в объеме кольца.
Линейная массовая плотность по отношению к углу поворота
dm/dθ равно отношению
М/2π
Следовательно, dm =M/2π dθ
Момент инерции — это интеграл от полной массы кольца от центра масс
я = ∫r2 dm
я = мистер2/ 2πθ
я = мистер2/ 2π * 2π
я = мистер2
Кинетическая энергия вращения кольца равна
Е = 1/2 Iω2
= 1/2 Мр2ω2
= 1/2 * 0.556 * 0.122* 1.82
= 0.013 Джоулей
Кинетическая энергия вращения кольца в точке равна 0.013 Дж.