Утверждение
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Дано:
∆ ABC,
∠C=90º,
∠A=30º.
Доказать:
![[BC = frac{1}{2}AB]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-079c3a0516262be534ab9a83be60f2cf_l3.png "Rendered by QuickLaTeX.com")
Доказательство:
I способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Проведем из вершины прямого угла медиану CF.
Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то
![[CF = frac{1}{2}AB,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a9a779ae05f7196b9a70c2cbc9c021cb_l3.png "Rendered by QuickLaTeX.com")
то есть, CF=AF=BF.
Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.
Следовательно, у него углы при основании равны:
∠B=∠BCF=60º.
Так как сумма углов треугольника равна 180º, то в треугольнике BFC
∠BFC =180º -(∠B+∠BCF)=60º.
Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.
Значит, все его стороны равны и
![[BC = CF = BF = frac{1}{2}AB]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-af056013a524dd68afc73d72fcdc266a_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
II способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º-∠A=90º-30º=60º.
Построим треугольник ADC, равный треугольнику ABC.
В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).
Отсюда, ∠BAD=∠CAD+∠CAB=60º.
Следовательно, в треугольнике ABD все углы равны:
∠BAD=∠D=∠B=60º.
Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.
BC=DC (по построению), поэтому
![[BC = frac{1}{2}BD = frac{1}{2}AB.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-690c38cc0c5d2e691b99af535a7fc517_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
Преподаватель который помогает студентам и школьникам в учёбе.
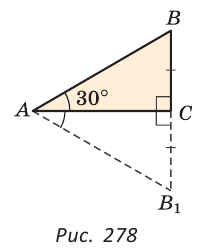
Свойство катета прямоугольного треугольника, лежащего против угла в 30°:
Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Дано: 
Доказать: ВС =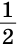 
АВ.
Доказательство:
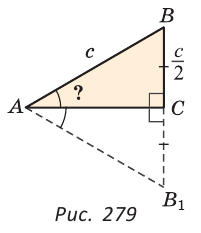
На луче ВС отложим отрезок СВ1 равный отрезку ВС. Так как АВ1С =АВС по двум катетам (катет АС — общий), то 
B1AC =
BAC = 30°,
BAB1 = 60°. Но В = В1 = 60°. Известно, что если у треугольника все углы равны, то он равносторонний. Отсюда АВВ1 — равносторонний, АВ = ВВ1, ВС = 
ВВ1 =
АВ. Теорема доказана.
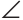
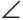
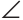
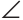
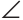
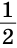
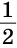
Верно и утверждение, обратное данному. Докажем его.
Теорема. Если в прямоугольном треугольнике катет равен половине гипотенузы, то этот катет лежит против угла в 30°.
Доказательство:
Пусть в треугольнике ABC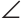 
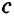
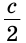
C = 90°, АВ = 
, ВС=
(рис. 279).
Докажем, что 
BAC = 30°. Продлим катет ВС на его длину: СВ1 = ВС. Из равенства прямоугольных треугольников АСВ1 и АСВ (по двум катетам) следует, что АВ1 = АВ = ВВ1 = . Значит, 
АВВ1 — равносторонний, все его углы равны по 60°, а его высота АС является биссектрисой. Поэтому BAC = 30°. Что и требовалось доказать.
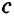
Пример:
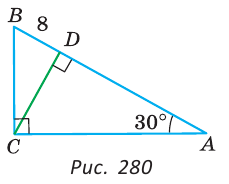
В прямоугольном треугольнике ABC, у которого C = 90°, A=30°, проведена высота CD. Найти отрезок AD, если BD = 8 см.
Решение:
Так как угол А и угол BCD дополняют угол В до 90°, то BCD=A=30° (рис. 280).
В прямоугольном треугольнике CDB катет BD лежит против угла в 30°. Поэтому СВ = 2BD = 16 см.
В треугольнике ABC катет ВС лежит против угла в 30°. Поэтому АВ = 2ВС = 32 см.
Отсюда AD=AB-BD = 32 — 8 = 24 (см).
Ответ: 24 см.
Замечание. Мы доказали, что BC = 2BD, AB = 2BC = 4BD, AD = АВ — BD = 3BD, то есть в прямоугольном треугольнике с углом 30° высота делит гипотенузу в отношении 1 : 3.
Пример:
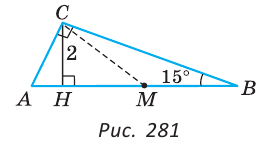
Дан прямоугольный треугольник с углом 15°. Высота, проведенная к гипотенузе, равна 2 см. Найти гипотенузу.
Решение:
Пусть в треугольнике ABC 
ACB = 90°, 
B = 15°, СН = 2 см — высота (рис. 281).
Нужно найти АВ. Проведем медиану СМ треугольника ABC. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то СМ = MB. Треугольник СМВ — равнобедренный, MCB = CBM = 15°, AMC — его внешний угол.
По свойству внешнего угла AMC =MCB +MBC = 15° + 15° = 30°.
В прямоугольном треугольнике СНМ катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы СМ. Отсюда СМ = 2СН = 4 см, АВ = 2СМ = 8 см.
Ответ: 8 см.
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
- Площадь параллелограмма
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Найти сторону треугольника, лежащую против угла в 30 градусов?
Геометрия | 5 — 9 классы
Найти сторону треугольника, лежащую против угла в 30 градусов.
Дано предоставленно во вложениях, ниже :
1) Опустим высоту ВД (Д лежит на АС).
Рассм тр АВД (уг Д = 90 * ) ВД = 1 / 2 * 1 = 0, 5 дм (по св — ву катета, лежащего напротив угла в 30 * ) ; уг АВД = 60 * ( по т о сумме углов треугольника : 180 * — 30 * — 90 * )
2) Рассм тр СДВ (уг Д = 90 * ) уг СВД = 45 * ( 105 * — 60 * = 45 * ), уг ВСД = 45 * ( по т о сумме углов треугольника : 180 * — 90 * — 45 * ) След тр СДВ — р / б ( по признаку р / б треуг — ка : уг В = уг С = 45 * )
Следовательно, ВД = СД = 0, 5 дм
3) по т Пифагора к тр СВД ( уг Д = 90 * ) получаем : ВС ^ 2 = 1 / 4 + 1 / 4 = 1 / 2, BC = корень из (1 / 2) дм = 1 / корень из (2) дм
Ответ : Г) 1 / корень из 2.
Две стороны треугольника равны 12 и 9 см, угол между ними 30 градусов, найти площадь треугольника — провести высоту и найти её как катет лежащий против угла 30 градусов?
Две стороны треугольника равны 12 и 9 см, угол между ними 30 градусов, найти площадь треугольника — провести высоту и найти её как катет лежащий против угла 30 градусов.
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 6 и 10 см?
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 6 и 10 см?
Гипотенуза прямоугольного треугольника равна 10 см, а один из углов – 30 градусов?
Гипотенуза прямоугольного треугольника равна 10 см, а один из углов – 30 градусов.
Найдите катет, лежащий против данного угла.
Помогите пожалуйста?
1)Построить треугольник по двум сторонам и углу, лежащему против большей из них.
2)Построить треугольник по двум сторонам и углу, лежащему против меньшей из них.
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 5 и 3?
Найдите сторону треугольника, лежащую против угла в 120 градусов, если две другие стороны равны 5 и 3.
Найти сторону треугольника, лежащую против его угла в 45°, если против второго угла этого треугольника градусной меры 60° расположена сторона длиной 3 см?
Найти сторону треугольника, лежащую против его угла в 45°, если против второго угла этого треугольника градусной меры 60° расположена сторона длиной 3 см.
Помогите?
Дан треугольник, один из углов которого равен 30 градусам.
Сторона треугольника, лежащая против угла в 30 градусов равна √13, а длины двух других сторон находятся в отношении 2 : 3√13.
Найдите длину наименьшей стороны треугольника.
Может ли наименьшая сторона треугольника лежать против угла 63°?
Может ли наименьшая сторона треугольника лежать против угла 63°?
Найдите сторону треугольника, лежащую против его угла в 45 градусов, если против второго угла этого треугольника градусной меры 60 градусов расположена сторона длиной : а)3см, б) , в)?
Найдите сторону треугольника, лежащую против его угла в 45 градусов, если против второго угла этого треугольника градусной меры 60 градусов расположена сторона длиной : а)3см, б) , в).
Найдите сторону треугольника лежащую против угла 45 градусов?
Найдите сторону треугольника лежащую против угла 45 градусов.
Вы перешли к вопросу Найти сторону треугольника, лежащую против угла в 30 градусов?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Треугольники АВС и А1В1С1 подобны, все их углы попарно равны. Если градусные меры относятся как 1 : 2 : 3, всего 6 частей, и сумма углов 180, то одна часть 180 / 6 = 30 градусов, а максимальный угол — это три части, 30 * 3 = 90 градусов. Если подоб..
11 см так как любые 2 стороны должны быть больше 1.
AB — средняя линия трапеции, она равна полсумме оснований ⇒ — PO — FE ОТВЕТ : PO = 18, FE = 12.
Из неравенств треугольников 5 + AB>18 , AB + 5>18, 23>AB следует что 13.
Надеюсь, все понятно Если что спрашивай.
Проще всего найти угол, для которого указан внешний. Он равен 180 — 110 = 70 градусов. Сумма всех углов равна 180. X + x + 14 + 70 = 180 2x = 96 x = 48, это меньший угол 48 + 14 = 62 и это последний угол.
Катет АС лежит против угла B угол B = 180 — 90 — 60 = 30 градусов. По опредению : катет лежещий против угла 30 градусов равен половине гипотенузы, находим этот катет : 16 / 2 = 8 дм. Ответ : катет АС = 8 дм.
Тут угол AMB = углуMAD = 34 BAM = AMB = 34 = > ABM = 112 В паралелограмме противоположные углы равны = > ABM = ADC = 112. Т. к. Сумма углов в 4ех угольнике равна 360 градусов = > С = (360 — 112×2) / 2 = = 68 градусов.
5 узлов делят веревку на 6 частей чтобы получить 7 частей нужно завязать 6 узлов.
Средняя линия — это полусумма оснований, если одно а второе b, то (a + b) / 2 = 6 Если в трапеции нарисовать диагональ, получить два треугольника, один с онованием a, второй с основанием b, и высотой для каждого из треугольников h = 17 то площади тре..
Треугольник. Свойство прямоугольного треугольника с углом в 30°.
Катет прямоугольного треугольника, противолежащий углу в 30°, будет равняться половине гипотенузы.
Изобразим прямоугольный треугольник АСВ с углом В = 30°. В этом случае второй его острый угол будет 60°.
Обоснуем, что катет АС равняется половине гипотенузы АВ то есть АС = 1/2АВ.
Продлим катет АС за вершину прямого угла С и начертим отрезок СМ, причем части равные СМ=АС. Прочертим ВМ, соединив таким образом точки В и М. Сформированные прямоугольные треугольники ВСМ и АСВ эквиваленты (равны по двум катетам). Наглядно видно, что всякий угол треугольника АМВ по 60°, значит можно сделать вывод, что образовавшийся треугольник — равносторонний.
Сторона АС = 1/2 АМ, а поскольку АМ = АВ, а значит и катет АС будет равен 1/2 гипотенузы АВ.
http://geometria.my-dict.ru/q/2607032_najti-storonu-treugolnika-lezasuu-protiv-ugla/
http://www.calc.ru/Treugolnik-Svoystvo-Pryamougolnogo-Treugolnika-S-Uglom-V-30.html
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
mat:geom:triangle:right
Содержание
Прямоугольный треугольник
Прямоугольный треугольник — треугольник, у которого один из углов – прямой.
Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос», которое означало отвес, перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», — для катетов;
«сторона, стягивающая прямой угол», — для гипотенузы.
В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Мнемоническое правило
Как запомнить где катет, а где гипотенуза, и не перепутать их.
Если сравнить названия сторон прямоугольного треугольника: «катет», «гипотенуза», то видим, что слово «гипотенуза» длиннее слова «катет». Так и в треугольнике: гипотенуза — самая длинная сторона.
Итак, ассоциация: катет — короткое слово, короткая сторона.
Гипотенуза — длинное слово, самая длинная из сторон.
Признаки равенства прямоугольных треугольников:
-
по двум катетам
-
по катету и гипотенузе
-
по катету и прилежащему острому углу
-
по катету и противолежащему острому углу
-
по гипотенузе и остром углу
Признаки подобия прямоугольных треугольников:
-
одному острому углу
-
из пропорциональности двух катетов
-
из пропорциональности катета и гипотенузы
Высота из вершины прямого угла
Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному
Доказательство следует из равенства углов треугольников.
Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике ABC длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной c на отрезки m и n, соответствующие катетам b и a, то
1) $ h^2 = mn $ или $ h = sqrt {mn} $
2) $hc = ab$ или $h = frac {ab} c$
Доказательство следует из подобия треугольников.
Высота есть среднее геометрическое проекций катетов на гипотенузу.
Высота есть произведение катетов, деленное на гипотенузу.
подробнее…
Проще доказать эти соотношения из нахождения косинуса, синуса и тангенса равных острых углов (но для этого нужно знать, что они у равных углов равны, а это вытекает из подобия треугольников. Но запоминается лучше). Для вывода второго соотношения еще можно приравнять площадь треугольника по друм формулам :
половина произведения катетов = половине произведения высоты на гипотенузу
YouTube — Всё про прямоугольный треугольник за 15 минут — Трушин
Сложением двух формул для $sin alpha + sin beta$ получается теорема Пифагора.
Медиана из вершины прямого угла
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы (и наоборот, если медиана равна половине стороны, то эта сторона лежит против прямого угла)
Для доказательства достроить до прямоугольника и посмотреть на диагонали.
Описанная окружность
Центр описанной окружности прямоугольного треугольника совпадает с серединой гипотенузы:
Радиус описанной окружности: $R = frac{c}{2}=m_c$
Катет против угла 30 градусов
Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы
живая модель
Для доказательства достроить до равностороннего треугольника.
Синус, косинус, тангенс, котангенс
В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.
Угол между биссектрисами
Острый угол между биссектрисами острых углов прямоугольного треугольника равен 45°.
легко доказать
· Последние изменения: 2020/02/04 20:29 —
kc