Как найти катет при угле 30 градусов

Как найти стороны прямоугольного треугольника

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Прямоугольный треугольник

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

  • для гипотенузы (с):
    • длины катетов a и b
    • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
  • для катета:
    • длину гипотенузы (с) и длину одного из катетов
    • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
    • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
    • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
    • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a =
Катет b =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

c = a/cos(β) = b/cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =

0

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

c = a/sin(α) = b/sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c =
Катет (известный) =
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c =
Угол (прилежащий катету) = °
Катет =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c =
Угол (противолежащий катету) = °
Катет =

0

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =

0

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

См. также

Источник

Известна гипотенуза AB и угол a

sin(a)=BC/AB

BC = sin(a) x AB

cos(a)=AC/AB

AC = cos(a) x AB

Как найти синус угла ?

Как найти косинус угла ?

Решение

Катет BC = sin(30) x 30 = 15

Катет AC = cos(30) x 30 = 25.9807621

Катеты прямоугольного треугольника с гипотенузой 30 и углом 30 равны 15 и 25.9807621

Ссылка на результат

?n1=30&n2=30

Источник

Утверждение

Катет, лежащий против угла 30 градусов, равен половине гипотенузы.

katet lezhaschiy protiv ugla 30

Дано:

∆ ABC,

∠C=90º,

∠A=30º.

Доказать:

    [BC = frac{1}{2}AB]

Доказательство:

I способ

Так как сумма острых углов прямоугольного треугольника равна 90º, то

∠B=90º-∠A=90º-30º=60º.

Проведем из вершины прямого угла медиану CF.

katet lezhaschiy protiv 30

Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то

    [CF = frac{1}{2}AB,]

то есть, CF=AF=BF.

Так как BF=CF, то  треугольник BFC — равнобедренный с основанием BC.

Следовательно, у него углы при основании равны:

∠B=∠BCF=60º.

Так как сумма углов треугольника равна 180º, то в треугольнике BFC

∠BFC =180º -(∠B+∠BCF)=60º.

Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.

Значит, все его стороны равны и

    [BC = CF = BF = frac{1}{2}AB]

Что и требовалось доказать.

II способ

Так как сумма острых углов прямоугольного треугольника равна 90º, то

∠B=90º-∠A=90º-30º=60º.

katet protiv ugla 30

Построим треугольник ADC, равный треугольнику ABC.

В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º  ( по построению).

Отсюда, ∠BAD=∠CAD+∠CAB=60º.

Следовательно, в треугольнике ABD все углы равны:

∠BAD=∠D=∠B=60º.

Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.

BC=DC (по построению), поэтому

    [BC = frac{1}{2}BD = frac{1}{2}AB.]

Что и требовалось доказать.

Источник

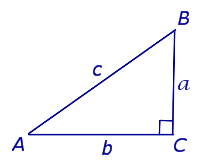
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$ $30$ $45$ $60$
$sinα$ $<1>/<2>$ $<√2>/<2>$ $<√3>/<2>$
$cosα$ $<√3>/<2>$ $<√2>/<2>$ $<1>/<2>$
$tgα$ $<√3>/<3>$ $1$ $√3$
$ctgα$ $√3$ $1$ $<√3>/<3>$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=<4>/<5>, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Треугольник. Свойство прямоугольного треугольника с углом в 30°.

Катет прямоугольного треугольника, противолежащий углу в 30°, будет равняться половине гипотенузы.

Изобразим прямоугольный треугольник АСВ с углом В = 30°. В этом случае второй его острый угол будет 60°.

Обоснуем, что катет АС равняется половине гипотенузы АВ то есть АС = 1/2АВ.

Продлим катет АС за вершину прямого угла С и начертим отрезок СМ, причем части равные СМ=АС. Прочертим ВМ, соединив таким образом точки В и М. Сформированные прямоугольные треугольники ВСМ и АСВ эквиваленты (равны по двум катетам). Наглядно видно, что всякий угол треугольника АМВ по 60°, значит можно сделать вывод, что образовавшийся треугольник — равносторонний.

Сторона АС = 1/2 АМ, а поскольку АМ = АВ, а значит и катет АС будет равен 1/2 гипотенузы АВ.

источники:

http://examer.ru/ege_po_matematike/teoriya/pryamougolnie_treugolniki

http://www.calc.ru/Treugolnik-Svoystvo-Pryamougolnogo-Treugolnika-S-Uglom-V-30.html

Источник

Содержание

Свойство

Катет прямоугольного треугольника, лежащий напротив угла в
$30^circ$, равен половине гипотенузы.

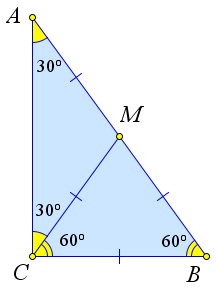
Доказательство

Рассмотрим треугольник $ABC$, в котором $angle C=90^circ, angle A=30^circ$.
Докажем, что $AB=2cdot CB$.

Пусть $CM$ – медиана.

Тогда $CM=MA=MB$, следовательно, $triangle AMC$ и $triangle BMC$ – равнобедренные.

Тогда $angle A=angle ACM$, следовательно, $angle MCB=angle CBM=60^circ$.

Тогда $triangle BCM$ – равносторонний, следовательно, $BC=BM=frac{1}{2}cdot AB$.

Первый признак

Если катет прямоугольного треугольника равен половине гипотенузы, то
угол, противолежащий этому катету, равен $30^circ$.

Доказательство

Рассмотрим прямоугольный треугольник $ABC$, в котором $angle C=90^circ, BC=frac{1}{2}cdot AB$.

Докажем, что $angle A=30^circ$.

Проведем медиану $CM$. Тогда по свойству медианы прямоугольного треугольника $CM = AM = BM$.

Тогда треугольник $CMB$ – равносторонний, а, значит $angle BCM = 60^circ.$

Тогда $angle ACM = 30^circ$.

И поскольку треугольник $ACM$ – равнобедренный, то $angle A = angle ACM = 30^circ.$

Второй признак

Если в треугольнике напротив угла в $30^circ$ лежит сторона, равная
половине другой стороны этого треугольника, то треугольник
прямоугольный.

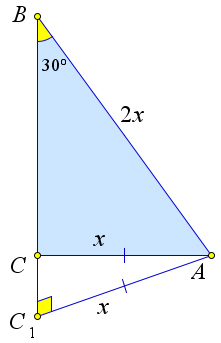
Доказательство

Первый способ.

Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, angle B=30^circ$.

Докажем, что тогда $angle C=90^circ$.

Предположим противное, тогда из точки $B$ можно опустить перпендикуляр $AC_1$ на прямую $CB$.

Треугольник $ABC_1$ – прямоугольный,$angle B=30^circ$, следовательно, $AC_1=x$.

Тогда $triangle CAC_1$ – равнобедренный, и $angle C_1=angle ACC_1=90^circ$, что невозможно.

Значит, $angle C=90^circ.$

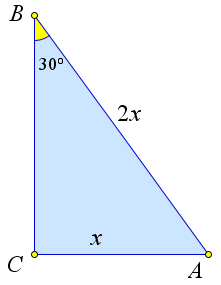
Второй способ.

Рассмотрим треугольник $ABC$, в котором $AC=x, AB=2x, angle B=30^circ$.

По теореме синусов для $triangle ABC$: $dfrac{x}{sin{30^circ}}=dfrac{2x}{sin{angle C}}$.

Тогда $sin{angle C}=1$, то есть $angle C=90^circ$.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Задача как найти абсолютную высоту
  • Как правильно составить исковое заявление на квартиру
  • Как найти сопротивление при резонансе напряжений
  • Как найти диспетчер телефона в телефоне самсунг
  • Как найти базы алгебра

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии