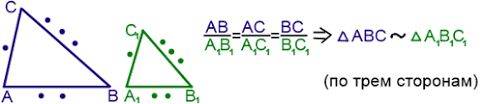Как найти катет подобного треугольника - AvtoShod.ru

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Подобие прямоугольных треугольников

Подобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

1- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по острому углу)

Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по острому углу).

2- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по двум катетам)

Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по двум катетам).

3- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по катету и гипотенузе)

Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.

— прямоугольные (∠C=90º, ∠C=90º).

(по катету и гипотенузе).

Из подобия прямоугольных треугольников следуют соотношения между высотой, проведённой к гипотенузе, гипотенузой, катетами и проекциями катетов на гипотенузу, а также свойство биссектрисы треугольника.

Как найти катет прямоугольного треугольника

С задачками по геометрии сталкиваются все в средней школе. Кому-то такие задачки даются сложно, а кто-то их щелкает, как орешки. На самом деле эти задачи не особо сложные, просто нужно вникнуть и понять определенный алгоритм решения. Давайте подробнее разберем, как найти катет прямоугольного треугольника.

Геометрические определения

Если у треугольника есть прямой угол (∠=90 о ), то он является прямоугольным.
Катет – линия, создающая угол 90 градусов в треугольнике.
Гипотенуза – линия, которая находится напротив угла равного 90 градусов.
Две ортогональные линии образуют прямой угол, величина которого 90 градусов. Еще можно сказать, что это половина развернутого угла.

Свойства сторон в прямоугольном треугольнике

Гипотенуза всегда больше каждого из катетов.

Сторона, которая находится напротив угла равного 30 градусов, равна половине величины гипотенузы.

К прямоугольному треугольнику можно применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Формулы для решения задач

Если мы знаем величину одного катета А и гипотенузы С, то второй катет B мы вычислим при помощи теоремы Пифагора.
Угол А мы может определись с помощью формулы синуса:

Так как сумма всех углов геометрической фигуры всегда равна 180 градусов, то другой острый угол можно вычислить по формуле:

Примеры решения задач

Задача №1:

В треугольнике АВС с ∠А=90 градусов, ∠С=60 градусов и катетом АВ=5 см. Найти длину катета АС.

В прямоугольном треугольнике АВС найдем угол В:

∠В=90 о — ∠С=90 о — 60 о = 30 о

Поскольку ∠В=30 о , то катет АВ равен половине гипотенузы ВС, а значит,

Длину катета АС найдем с помощью теоремы Пифагора:

Задача №2:

В равнобедренном и прямоугольном треугольнике АВС гипотенуза больше катета на 2 см. Найти длину сторон треугольника.

В треугольной фигуре АВС обозначим катеты АВ=АС=х, тогда ВС=2+х. Запишем теорему Пифагора для данного треугольника:

ВС 2 = АВ 2 + АС 2 => (х+2) 2 = х 2 + х 2 или х 2 – 4х – 4 = 0

Решая это уравнение и учитывая условия задачи, получим

т.е. АВ = АС = (2+2) см, ВС = (4+2) см

Ответ: АВ = АС = (2+2) см, ВС = (4+2) см

Как видите, процесс решения геометрических задач по нахождению катета в прямоугольном треугольнике не особо сложный. Нужно просто приложить усилия, посидеть и вникнуть в суть задачи. Когда начнете писать формулы, решение придет к вам само. Удачи в решении задачек по геометрии, теперь вы знаете, как найти катет прямоугольного треугольника.

источники:

Подобие прямоугольных треугольников

http://dobriy-sovet.ru/kak-najti-katet-pryamougolnogo-treugolnika/

Источник

Признаки подобия прямоугольных треугольников

1- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по острому углу)

Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.

$[Delta ABCuDelta {A_1}{B_1}{C_1}]$

— прямоугольные (∠C=90º, ∠C=90º).

Если

$[angle B = angle {B_1},]$

то

$[Delta ABC sim Delta {A_1}{B_1}{C_1}]$

(по острому углу).

2- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по двум катетам)

$[Delta ABCuDelta {A_1}{B_1}{C_1}]$

— прямоугольные (∠C=90º, ∠C=90º).

Если

$[frac{{BC}}{{{B_1}{C_1}}} = frac{{AC}}{{{A_1}{C_1}}},]$

то

$[Delta ABC sim Delta {A_1}{B_1}{C_1}]$

(по двум катетам).

3- й признак подобия прямоугольных треугольников

( подобие прямоугольных треугольников по катету и гипотенузе)

$[Delta ABCuDelta {A_1}{B_1}{C_1}]$

— прямоугольные (∠C=90º, ∠C=90º).

Если

$[frac{{BC}}{{{B_1}{C_1}}} = frac{{AB}}{{{A_1}{B_1}}},]$

то

$[Delta ABC sim Delta {A_1}{B_1}{C_1}]$

(по катету и гипотенузе).

Источник

mat:geom:triangle:right

Содержание

Прямоугольный треугольник

Прямоугольный треугольник — треугольник, у которого один из углов – прямой.

Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос», которое означало отвес, перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», — для катетов;
«сторона, стягивающая прямой угол», — для гипотенузы.

В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Мнемоническое правило

Как запомнить где катет, а где гипотенуза, и не перепутать их.

Если сравнить названия сторон прямоугольного треугольника: «катет», «гипотенуза», то видим, что слово «гипотенуза» длиннее слова «катет». Так и в треугольнике: гипотенуза — самая длинная сторона.

Итак, ассоциация: катет — короткое слово, короткая сторона.

Гипотенуза — длинное слово, самая длинная из сторон.

Признаки равенства прямоугольных треугольников:

по двум катетам
по катету и гипотенузе
по катету и прилежащему острому углу
по катету и противолежащему острому углу
по гипотенузе и остром углу

Признаки подобия прямоугольных треугольников:

одному острому углу
из пропорциональности двух катетов
из пропорциональности катета и гипотенузы

Высота из вершины прямого угла

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному

Доказательство следует из равенства углов треугольников.

Теорема о высоте прямоугольного треугольника

Если высота в прямоугольном треугольнике ABC длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной c на отрезки m и n, соответствующие катетам b и a, то

1) $ h^2 = mn $ или $ h = sqrt {mn} $

2) $hc = ab$ или $h = frac {ab} c$

Доказательство следует из подобия треугольников.

Высота есть среднее геометрическое проекций катетов на гипотенузу.

Высота есть произведение катетов, деленное на гипотенузу.

подробнее…

Проще доказать эти соотношения из нахождения косинуса, синуса и тангенса равных острых углов (но для этого нужно знать, что они у равных углов равны, а это вытекает из подобия треугольников. Но запоминается лучше). Для вывода второго соотношения еще можно приравнять площадь треугольника по друм формулам :

половина произведения катетов = половине произведения высоты на гипотенузу

YouTube — Всё про прямоугольный треугольник за 15 минут — Трушин

Сложением двух формул для $sin alpha + sin beta$ получается теорема Пифагора.

Медиана из вершины прямого угла

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы (и наоборот, если медиана равна половине стороны, то эта сторона лежит против прямого угла)

Для доказательства достроить до прямоугольника и посмотреть на диагонали.

Описанная окружность

Центр описанной окружности прямоугольного треугольника совпадает с серединой гипотенузы:

Радиус описанной окружности: $R = frac{c}{2}=m_c$

Катет против угла 30 градусов

Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы

живая модель

Для доказательства достроить до равностороннего треугольника.

Синус, косинус, тангенс, котангенс

В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.

В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.

Угол между биссектрисами

Острый угол между биссектрисами острых углов прямоугольного треугольника равен 45°.

легко доказать

mat/geom/triangle/right.txt

· Последние изменения: 2020/02/04 20:29 —

Источник

Признаки подобия прямоугольных треугольников

Средняя оценка: 4

Всего получено оценок: 127.

Средняя оценка: 4

Всего получено оценок: 127.

Подобие – это следующее понятие после равенства: как в математике после сложения идет умножение, так в геометрии после равенства треугольников изучают подобие. В реальной жизни подобие помогает, за счет вычислений по тени, определять реальные размеры зданий или высоких сооружений. В задачах на эту тему, благодаря подобию, можно найти значение сторон, воспользовавшись знакомым отношением.

Определения

Подобными называются треугольники, отношение сторон которых соответственно равны. Предположим треугольник АВС равен треугольнику DРН. Это значит, что:

$${АВover{DP}}={BCover{PH}}={ACover{DH}}=k$$

k это коэффициент подобия.

Для обычного треугольника существует три признака подобия. Именно через них доказываются признаки подобия прямоугольных треугольников.

Первый признак подобия: по двум углам. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Рис. 1. Первый признак подобия.

Второй признак: по трем сторонам. Если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.

Рис. 2. Второй признак подобия.

Третий признак: по двум сторонам и углу. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то такие треугольники подобны.

Рис. 3. Третий признак подобия.

Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

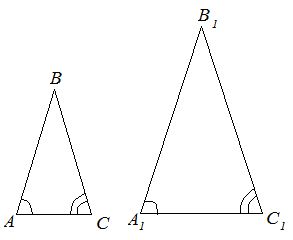
Первый признак по острому углу: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Доказать этот признак очень просто. Достаточно вспомнить, что прямоугольным треугольником называется треугольник, который содержит в себе прямой угол. Значит, у двух прямоугольных треугольников, один из углов всегда равен другому. А один из острых углов так же равен соответственному углу в другом треугольнике. Значит, в таких треугольниках есть два равных между собой угла, и треугольники подобны по первому признаку подобия.

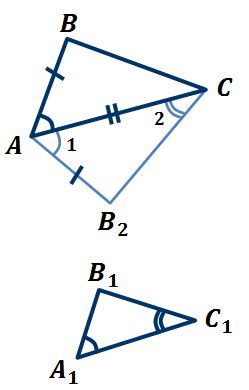
Второй признак: по двум катетам. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. Между двумя катетами всегда заключен прямой угол. Значит, у нас имеется две пропорциональные стороны и равные углы между ними. Тогда треугольники подобны по третьему признаку подобия.
Третий признак: по катету и гипотенузе. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны. Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.

$$cos(ACB)={BCover{AC}}$$

$$cos(DHP)={PHover{DH}}$$

При этом по условию: $${ACover{DH}}={BCover{PH}}$$. Из условия выразим ВС и подставим в значение косинуса.

$$ВС=РН*{АCover{DН}}$$

$$cos(ACB)={BCover{AC}}={PH*{ACover{DH}}over AC}={PHover{AC}}$$ – то есть косинусы углов равны, оба угла острые, значит и углы равны. Тогда треугольники подобны по двум сторонам и углу между ними.

Что мы узнали?

Мы разобрали понятие подобия, выделили все определения и теоремы, необходимые для доказательства трех признаков подобия прямоугольных треугольников. Мы показали, что эти признаки лишь следствие основных, т.е. эти свойства созданы чтобы упростить и сделать быстрее решение. А это значит, что если вдруг вы забыли признаки для прямоугольного треугольника, то всегда можно воспользоваться общими.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

Средняя оценка: 4

Всего получено оценок: 127.

А какая ваша оценка?

Источник

ВИДЕОУРОК

Две фигуры подобны, если каждой точке одной
фигуры можно сопоставить точку другой фигуры так, что для любых двух точек А и В одной
фигуры и сопоставимых им точек А₁ и В₁ другой фигуры выполняется условие

где k – одно и то же положительное число для всех точек.

Число k – коэффициент подобия фигур.

Признаки подобия прямоугольных
треугольников.

Два прямоугольных
треугольника подобны между собой, если:

– острый угол
одного треугольника равен острому углу другого треугольника;

– катеты одного
треугольника пропорциональны катетам другого треугольника;

– гипотенуза и
катет одного треугольника пропорциональны гипотенузе и катету другого
треугольника.

Отношение периметров
подобных прямоугольных треугольников равно отношению сходственных сторон
(коэффициенту подобия):

Отношение площадей
подобных прямоугольных треугольников равно квадрату отношения соответствующих
сторон (квадрату коэффициента подобности).

Высота
прямоугольного треугольника, проведённая из вершины прямого угла, делит
треугольник на два подобных треугольника, каждый из которых подобен данному
треугольнику.

ПРИМЕР:

∆ АВС, ∠ С = 90°, СМ – высота,

∆ АМС ∼ ∆ СМВ.

При проведении всех
трёх средних линий образуется 4 равных
треугольника, подобных исходному с коэффициентом ¹/_2.

ЗАДАЧА:

Параллельные прямые ВС и DЕ пересекают стороны угла А, изображённого
на рисунку.

АВ = 6 см,

АС = 4 см,

СE = 2 см.

Найдите длину отрезка АD.

РЕШЕНИЕ:

∆ ABC
~ ∆ ADE, тогда

ОТВЕТ: 9 см

ЗАДАЧА:

По данным, изображённым на
рисунку, найдите высоту дерева.

РЕШЕНИЕ:

ЗАДАЧА:

Середина боковой стороны равнобедренного треугольника удалена
от его основания на 9 см. Найдите расстояние от точки пересечения медиан треугольника
до его основания.

РЕШЕНИЕ:

Начертим чертёж.

Треугольники АМD и АКL – подобные.

MD = 6 (см).

ЗАДАЧА:

Отрезки АС и СD, изображённые на
рисунку,

параллельны,

∠
АВС = 90°, АВ
= 24 см,

ВО = 10
см, СО = 5 см.

Найдите длину отрезка АD.

РЕШЕНИЕ:

СD ∥
АВ, ∠ АВС = 90°,

АВ = 24 см,

ВО = 10 см,

СО = 5 см.

Так как

СD ∥
АВ і
AВ ⊥ ВС, то

DС ⊥ ВС, то есть

∠ ВСD = 90°.

Из ∆ AВО (∠ В = 90°):

∠ АОВ = ∠ DОС как вертикальные.

∆ DСО ~ ∆ AВО,

Поэтому,

AD = AO + OD =

= 26 + 13 = 39 см.

ОТВЕТ: 39 см

ЗАДАЧА:

В треугольнике АВС отрезок ВК –
высота, отрезок АМ – биссектриса,

ВК = 26 см,

АВ : АС
= 6 : 7.

Из точки М опущен
перпендикуляр МD на сторону
АС. Найдите отрезок МD.

РЕШЕНИЕ:

Начертим чертёж.

По свойству биссектрисы треугольника имеем:

ВМ : МС = АВ : АС = 6 : 7.

Пусть ВМ = 6х,
тогда

МС = 7х,

ВС = 6х + 7х = 13х.

По условию, ВК ⊥
АС и

МD ⊥ АС.

Поэтому ВК
∥ МD и

∆ СВК ~ ∆ СМD.

Откуда:

ВК : МD = ВС : МС,

26 : МD = 13х : 7х.

ОТВЕТ: 14 см

ЗАДАЧА:

Окружность, центр которой принадлежит гипотенузе прямоугольного
треугольника, касается большого катета и проходит через вершину противоположного
острого угла. Найдите радиус окружности, если катеты равны 5
см и
12
см.

РЕШЕНИЕ:

Пусть треугольник АСВ (∠ С = 90°) – данный прямоугольный
треугольник,

АС = 5 см, ВС = 12
см,

О –
центр окружности,

ОD ⊥ ВС, D –
точка касания окружности с центром О до катета ВС,

ОD = ОА –
радиус окружности.

Из прямоугольного треугольника АСВ имеем:

Поэтому ОD
∥ АС и треугольники АСВ и ОDВ подобные.

Нехай

ОD = ОА = х.

Тогда ОВ = 13 – х.

Получим:

ОВ : ОD = АВ : АС,

(13 – х) : х = 13 : 5,

(13 – х) ∙ 5
= 13x,

65 – 5х = 13х, 18х = 65,

х = 65 : 18, х = 3¹¹/₁₈,

Поэтому, радиус окружности равен 3¹¹/₁₈
см.

ОТВЕТ: 3¹¹/₁₈ см

ЗАДАЧА:

Катет прямоугольного треугольника равен 8 см,
а гипотенуза – 16 см. Найдите проекцию данного катета на гипотенузу.

РЕШЕНИЕ:

Начертим чертёж.

∆ АВС ~ ∆ ВDС, поэтому

ЗАДАЧА:

Боковая сторона равнобедренного треугольника точкою касания
вписанной окружности делится в отношении
8
: 9, считая
от вершины угла при основании треугольника. Найдите площадь треугольника, если
радиус вписанной окружности равен 16 см.

РЕШЕНИЕ:

Пусть АВС – равнобедренный
треугольник (АВ = ВС) с центром вписанной окружности О,

К – точка касания окружности до стороны ВС,

ОК = 16 см,

СК : КВ
= 8 : 9.

Пусть СК = 8х,
тогда

ВК = 9х,

ВС = 8х + 9х = 17х (см).

Проведем высоту ВD треугольника. Треугольник ОКВ прямоугольный

(∠ К = 90°), тому

По свойству касательных, проведённых из одной точки до окружности,

СD = СК = 8х.

Из подобности прямоугольных треугольников ВОК и ВСD (у них общий острый угол) получим:

256 + 81х² = 1156,

81х² = 900, х² = ⁹⁰⁰/₈₁,

х =
¹⁰/₃.

DС = 8х = ¹⁰/₃ ∙ 8
= ⁸⁰/₃ (см).

ВС = 17х
= 17 ∙ ¹⁰/₃ = ¹⁷⁰/₃ (см).

Р = 2 ∙ (⁸⁰/₃ + ¹⁷⁰/₃) = ⁵⁰⁰/₃ (см).

S_∆ABC = ¹/₂ р ∙ r = ¹/₂ ∙ ⁵⁰⁰/₃ ∙16
=

= ⁴⁰⁰⁰/₃ = 1333¹/₃ (см²).

ОТВЕТ: 1333¹/₃ см²

ЗАДАЧА:

Центр окружности, вписанной в равнобедренный треугольник,
делить его высоту, проведённую до основания, на отрезки, длины которых равны 10
см и
26
см. Найдите площадь данного треугольника.

РЕШЕНИЕ:

Пусть АВС – заданный равнобедренный треугольник (АВ = ВС),

О –
центр вписанной окружности,

ВD –
высота треугольника,

ОD = 10 см, ОВ = 26 см,

К – точка касания кола до боковой стороны АВ,

ОК = ОD = 10 см.

Из прямоугольного
треугольника ВКО (∠ К = 90°) имеем:

ВD = ВО + ОD =

= 26 + 10 = 36 (см).

Из подобных прямоугольных треугольников

АВD і ОВК имеем:

АD : ВD = КО : КВ,

АD : 36
= 10 : 24

Находим площадь треугольника АВС.

S_ABC = ¹/₂ AC ∙
BD =

= AD ∙
BD
=

=
15 ∙ 36 = 540 (см²).

ОТВЕТ: 540 см²

ЗАДАЧА:

На медиане ВD равнобедренного
треугольника АВС (АС = ВС) взята точка
К такая, что
КD = 2ВК.
Прямая АК пересекает сторону ВС в точке
М.
Найдите площадь треугольника АМС, если площадь треугольника АВС равна 20.

РЕШЕНИЕ:

Начертим чертёж.

ВD –
медиана треугольника АВС, проведённая к его основанию, следовательно, ВD является высотой
и биссектрисой. Проведём прямую ВF параллельную АС до пересечения её с продолжением АМ в точке F.
Пусть

АD = DС = х, АС = 2х.

Треугольник АКD подобен
треугольнику FКВ по двум углам

(∠ КAD
= ∠ КFB, ∠ AKD = ∠ FKB),

следовательноотсюда

BF = ¹/₂ AD = ¹/₂ x.

Треугольник АMC подобен
треугольнику FMB

(∠ AMC
= ∠ FMB, ∠ MAC = ∠ MFB),

поэтому

отсюда

BF = ¹/₂ AD = ¹/₂ x.

Треугольник АMC подобен
треугольнику FMB

(∠ AMC
= ∠ FMB, ∠ MAC = ∠ MFB),

поэтому

Треугольники АВС и АМС имеют
одинаковую высоту, проведённую из вершины
А. Следовательно их площади относятся также, как
стороны к которым эта высота проведена.

отсюда получим, что

S_AМC = ⁴/₅ S_AВС=

= ⁴/₅∙ 20 = 16.

ЗАДАЧА:

Диагональ равнобедренной трапеции перпендикулярна до боковой
стороны, а основание равно 28 см и 100
см. Найдите длины отрезков, на которые высота трапеции, проведённая из вершины
тупого угла, делит диагональ.

РЕШЕНИЕ:

Пусть АВСD (АВ ∥ СD) – равнобедренная трапеция,

ВЕ и СК – высоты,

АС ⊥ СD,

ВС = 28 см,

АD = 100 см,

О –
точка пересечения прямых АС и ВЕ.
Проведём медиану СМ треугольника АСD (∠ С
= 90°). По свойству медианы, проведённой из вершины прямого угла
прямоугольного треугольника, получим

СМ = АМ = МD = 50 (см).

MK = MD – KD =

= 50 – 36
= 14 (см).

Из треугольника
МКС (∠ К = 90°) имеем:

Из треугольника АКС (∠ К = 90°) имеем:

∆ AOE ~ ∆ СOB,

(∠ OAE = ∠ OCB, ∠ OBC = ∠ OEA), тому

откуда

Пусть АО = 9х (см), тогда

ОС = 7х (см).

АО + ОС = АС,

9х + 7х = 80, х = 5 (см).

АО = 45 см, ОС = 35 см.

ОТВЕТ: 45 см, 35 см

ЗАДАЧА:

Два равных равнобедренных прямоугольных
треугольника с катетами а расположены так, что катет ВС ∆ АВС параллельный гипотенузе А₁В₁ ∆ А₁В₁C₁. Вершины В и С соответственно лежат на катетах А₁C₁ и В₁C₁. Определите площадь трапеции BCMN.

РЕШЕНИЕ:

Из ∆ АВN выходит, что

MN = AM = a – MC.

∆ А₁C₁B₁ ~ ∆ BCC₁, поэтому

то есть

Откуда

MC = a(√͞͞͞͞͞2– 1);

MN = a(2
– √͞͞͞͞͞2 );

Поэтому,

Задания к уроку 15

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Единицы измерения площади
Урок 2. Площадь прямоугольника
Урок 3. Площадь квадрата
Урок 4. Площадь треугольника
Урок 5. Площадь прямоугольного треугольника
Урок 6. Площадь равнобедренного треугольника
Урок 7. Площадь параллелограмма
Урок 8. Площадь ромба
Урок 9. Площадь трапеции
Урок 10. Площадь равнобедренной трапеции
Урок 11. Площадь прямругольной трапеции
Урок 12. Площадь круга и его частей
Урок 13. Подобие разносторонних треугольников
Урок 14. Подобие равнобедренных треугольников
Урок 16. Площадь многоугольника

Источник

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Формула

Пример

Найти гипотенузу по катету и прилежащему к нему острому углу

Формула

Пример

Найти гипотенузу по катету и противолежащему к нему острому углу

Формула

Пример

Найти гипотенузу по двум углам

Найти катет

Найти катет по гипотенузе и катету

Формула

Пример

Найти катет по гипотенузе и прилежащему к нему острому углу

Формула

Пример

Найти катет по гипотенузе и противолежащему к нему острому углу

Формула

Пример

Найти катет по второму катету и прилежащему к нему острому углу

Формула

Пример

Найти катет по второму катету и противолежащему к нему острому углу

Формула

Пример

Подобие прямоугольных треугольников

Как найти катет прямоугольного треугольника

Геометрические определения

Свойства сторон в прямоугольном треугольнике

Формулы для решения задач

Примеры решения задач

Задача №1:

Задача №2:

Содержание

Прямоугольный треугольник

Мнемоническое правило

Признаки равенства прямоугольных треугольников:

Признаки подобия прямоугольных треугольников:

Высота из вершины прямого угла

Теорема о высоте прямоугольного треугольника

Медиана из вершины прямого угла

Описанная окружность

Катет против угла 30 градусов

Синус, косинус, тангенс, котангенс

Угол между биссектрисами

Признаки подобия прямоугольных треугольников

Определения

Признаки подобия прямоугольных треугольников

Что мы узнали?

Тест по теме

Оценка статьи

Не пропустите также: